基于負磁致伸縮效應的電機降噪方法研究
張 欣, 宋子晗, 王文斌, 韓 瑜, 祝麗花
(天津工業大學 天津市電工電能新技術重點實驗室,天津 300387)
電機被廣泛應用于人類生活中,尤其應用于艦船驅動等軍工領域以及重工業行業等對大型電機的低噪聲要求更加嚴格,永磁同步電機的平穩和安靜運行性能在高性能應用中非常重要。
電機的振動噪聲研究起源于20世紀30年代,而磁致伸縮效應是在1842年由英國學者發現的。在2004年美國學者Mohammed等[1]測量了逆向磁致伸縮對電工鋼的磁化特性的影響,并用虛功原理計算出了磁致伸縮力。Zhu等[2]建立了包括磁致伸縮的磁彈耦合模型,用于疊片鐵心的振動分析,然后應用數值模型并測量磁化強度和MS曲線,分析發現定子中的變形不僅由磁阻力引起,還由磁致伸縮效應和諧波引起,而且磁致伸縮和諧波非常重要,這對于設計更低振動和噪聲的電動機很有意義。Ghalamestani等[3]同時考慮電磁力和磁致伸縮力對電機定子的影響,用等效力表示出了電機定子的形變,分析發現電磁力和磁致伸縮力在一定情況下會互相增強和抵消。
韓雪巖對電工硅鋼片的磁致伸縮特性和不同電流下的電機振動噪聲進行了測量和分析,發現當考慮磁致伸縮效應時,測試結果更接近實際值[4-5]。祝麗花[6]測量了硅鋼片在有無絕緣層時磁致伸縮效應對應力的影響以及變壓器鐵心硅鋼片鐵軛和中柱在軋制方向與垂直方向的應力與應變的關系。張欣等[7]通過對不同類型的電機進行定子振動響應測試,發現電機定子硅鋼片的主要振動頻率為供電頻率的一倍和二倍電源頻率處,而且以二倍供電頻率為主。吳勝男等[8]通過建立電機定子解析模型對定子振動與磁致伸縮的關系進行了解析計算,發現由磁致伸縮效應引起的定子上的振動與硅鋼片的磁致伸縮系數成正比。閆榮格等[9-10]測試了不同含量諧波情況下的電機振動加速度與電機的應力分布情況,分析了不同諧波對電機振動噪聲的影響。馮大軍等[11]對不同種類的硅鋼片在不同退火工藝下進行了磁致伸縮性能測試,發現磁致伸縮與退火時間和磁化方向等因素有關。Kuroishi等[12]通過進行靜磁耦合和結構有限元分析來估計定子的振動形狀,并與在每個邊帶頻率上計算出的振動形狀進行了對比試驗。Yamagashira等[13]在旋轉通量條件下,測量了非定向電工鋼板二維磁致伸縮特性,明確了磁通密度向量,磁場強度向量和二維磁致伸縮之間的關系。
Belahcen[14]研究發現在考慮耦合時,同步發電機定子的計算振動是不同的。取決于所考慮的振動頻率,由于磁彈性耦合,觀察到振動幅度的增大或減小大約20%。Zhang等[15]測量并分析了交變磁化加直流偏置下硅鋼片的磁致伸縮各向異性和應力依賴性,提出了一種利用直流偏置下的磁致伸縮曲線的磁性有限元分析方法。孫小光[16]通過Matlab繪制了電機定子中磁致伸縮力與外加磁場方向和大小的插值曲面圖,發現磁致伸縮力的方向與磁場方向相同且大小相關。王園弟等[17]對旋轉磁化下的無取向硅鋼片進行了應力分析,發現磁致伸縮效應下的鐵軛應變主要是平行軋制方向,而定子齒部最大應變則垂直與鐵軛應變的方向。郝清亮等[18]通過試驗對比了磁致伸縮力和麥克斯韋力對電機振動噪聲的貢獻分析,發現雖然磁致伸縮力的貢獻小于麥克斯韋力,但對磁致伸縮力的研究也是非常重要的。馮旭[19]對無取向硅鋼片在交變磁場中的磁致伸縮效應進行分析,又對永磁同步電機的振動進行了試驗測試,發現當考慮磁致伸縮效應時電機的振動噪聲大于不考慮磁致伸縮效應時的振動噪聲。Xiao等[20]提出了一種解耦方法來處理鐵磁材料中的磁致伸縮效應和反磁致伸縮效應的計算。將從磁場溶液中導出的磁致伸縮轉換為體積力密度,并將其用作外部載荷,通過沿每個局部主軸重構非線性BH曲線,可以考慮反磁致伸縮對磁場的影響。趙小軍等[21]中構建了硅鋼片的直流偏磁動態磁致模型,用于模擬硅鋼片在直流偏磁下的損耗特性。翁玲等[22]測量了多種磁致伸縮材料在不同磁感應強度和勵磁頻率下的磁導率以及電磁損耗情況。
電磁力導致的振動噪聲和磁致伸縮力導致的振動噪聲可以分別采取一定方法來降低,最終降低電機整體振動噪聲。目前電磁力部分的噪聲問題已經有很多成熟的降噪方案,而由磁致伸縮力導致的振動噪聲的抑制方法還鮮有研究。本文提出通過填充具有負磁致伸縮特性的軟磁復合材料來抑制電機振動噪聲的方法,使擬填充材料的負磁致伸縮與硅鋼片的正磁致伸縮效應引起的形變基本相互抵消,從而減小電機的振動噪聲。首先建立電機定子的電磁-機械耦合數值模型進行有限元計算仿真,對電機定子填充負磁致伸縮材料,同時比較了不同填充位置和距離對定子面應力的影響情況。然后根據有限元仿真結果搭建了電機定子應變測量試驗平臺,通過對實際電機定子打孔并填充負磁致伸縮材料鎳進行試驗,驗證了有限元計算的結果。
1 數學模型
首先建立考慮磁致伸縮效應的電磁-機械的耦合模型,為了測試負磁致伸縮材料對電機定子振動噪聲的影響,本文選取有限元仿真軟件COMSOL Multiphysics建立了二維模型,對電機定子進行了仿真試驗。其磁-機械耦合數值模型可用以下公式表示
[S][A]=[Je]
(1)
[K][U]=[F]
(2)
式中:K表示機械剛度矩陣;S表示電磁剛度矩陣;Je是外部電流密度雅可比矩陣;F是作用力;通過求解得到振動位移U;矢量磁勢A。
固體力學中線彈性材料的研究方程

(3)
F=I+?u
(4)
式中:u表示位移矢量;F是載荷量;ρ表示密度;S是應變;υ代表泊松比。
對于彈性張量D,在三維線彈性材料中可表示為
(5)
在有限元中固體力學模塊的求解方程如下所示
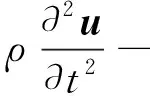
(6)
T-Ti=C(S-Si)
(7)
式中:ρ是密度;μ是位移矢量;F是載荷量;T是所受應力;Ti是所給出的應力的初值;C是剛度矩陣;Si是初始應變設定值。
對于電機定子硅鋼片來說,其磁致伸縮面的應力求解公式為
σ=Dξ
(8)
式中:σ為磁致伸縮應力;D為彈性張量;ξ為磁致伸縮應變。
2 仿真結果與分析
本文采用金屬鎳作為填充材料,首先鎳容易成型,比較容易獲得,而且有著很好的機械強度和延展性,同時空氣中不易氧化,具備負磁致伸縮性能,所以本次試驗選用鎳(Ni)進行了試驗。Ni的參數如表1所示。而后基于以上的數學模型對永磁同步電機的定子模型進行了限元仿真,包括打孔填充負磁致伸縮材料前后電機定子的面應力變化情況以及點應力變化情況對比。

表1 Ni的屬性值
2.1 初始條件
在有限元仿真軟件COMSOLMultiphysics構建電機定子模型,為了減少轉子磁場對定子的影響,本試驗去掉了電機轉子,這樣可以減小外部氣隙中的漏磁,從而使磁通主要集中在定子鐵心內部,減小電機定子齒表面的電磁力,使電機定子鐵心的主要應力為磁致伸縮力。
2.2 電機定子面應力仿真結果
圖1為電機定子填充負磁致伸縮材料前的局部面應力分布情況,圖2為打孔填充負磁致伸縮材料后的局部面應力分布。兩圖對比發現,在定子填充負磁致伸縮材料后最大面應力由1.69×107N/m2減小到1.67×107N/m2,變化量很少,但是可以明顯地看出圖2中左上方深色區域(應力較大區域)明顯減少了。為了更直接的看出負磁致伸縮材料填充前后的應力變化情況,于是對圖3中三個位置A、B、C處的點應力分別進行了測量。
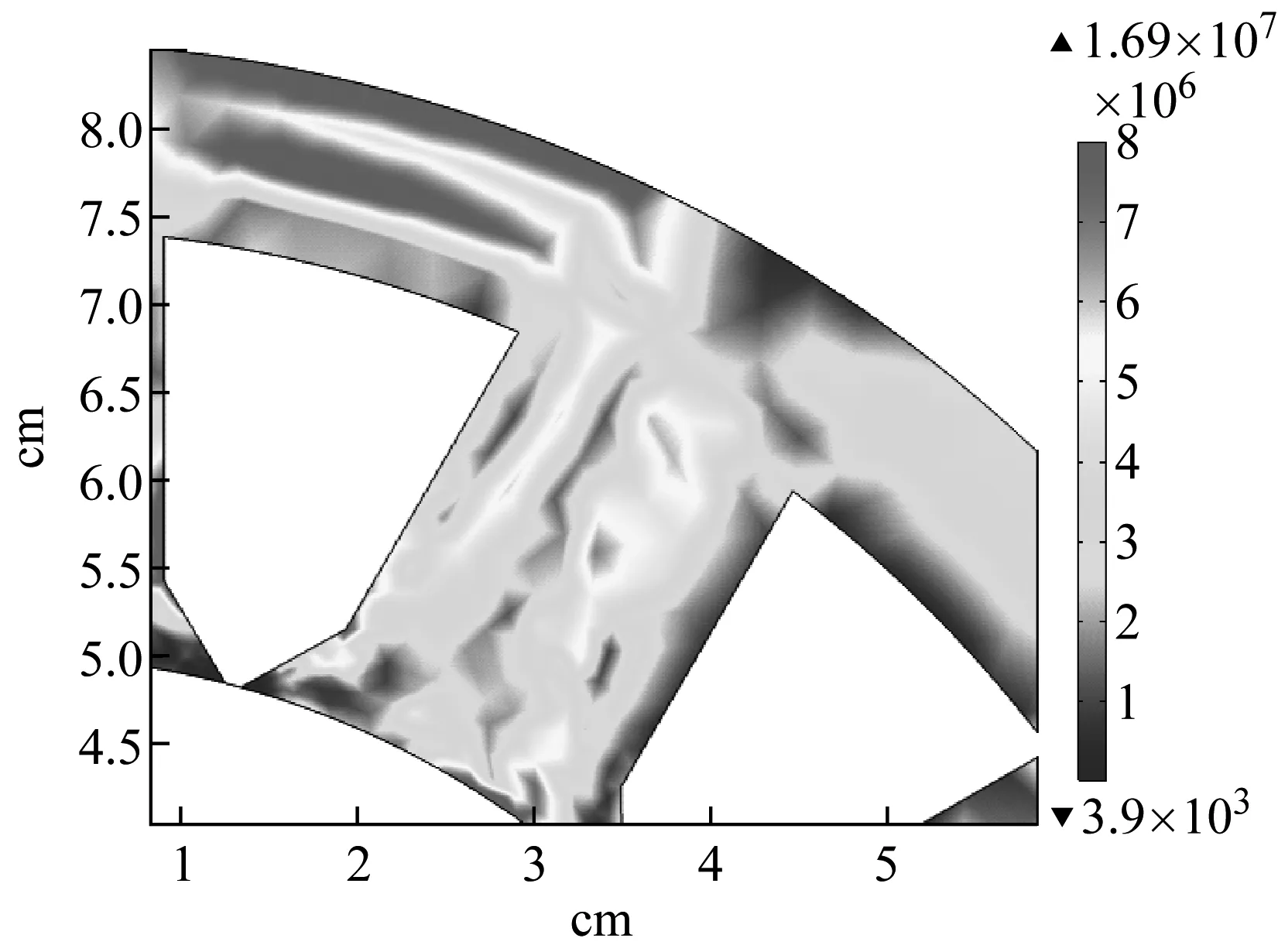
圖1 未打孔時局部應力
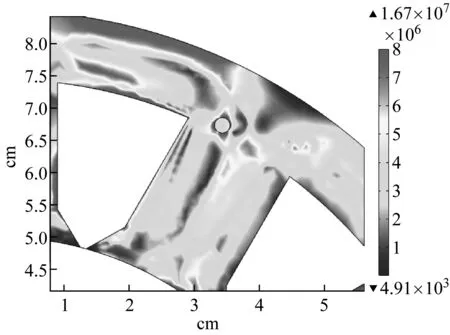
圖2 打孔填充后局部應力
2.3 電機定子點應力仿真結果
如圖3所示,選取的三個測量點為A、B、C,點A位于打孔附近區域,點B和點C距離打孔位置較遠,由圖4和圖5可以看出在打孔添加負磁致伸縮材料后測量點的應力變化情況。
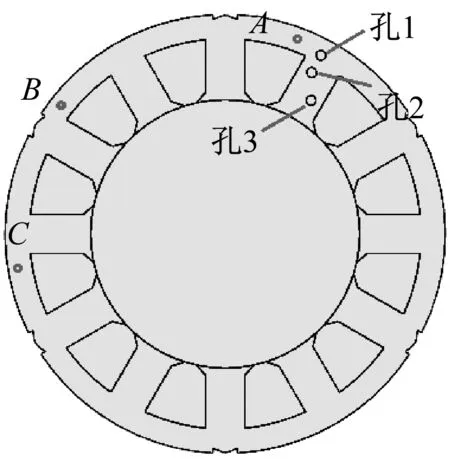
圖3 測量點
在本次仿真中孔3為填充負磁致伸縮材料的一個較優點,孔1和孔2為隨機兩個位置。
較優點尋找方法為:首先在COMSOL中設定打孔的形狀為圓形,打孔半徑為r,孔圓心到定子模型中心距離為R,孔圓心與定子模型中心連線與水平方向夾角為angle,如圖4所示。
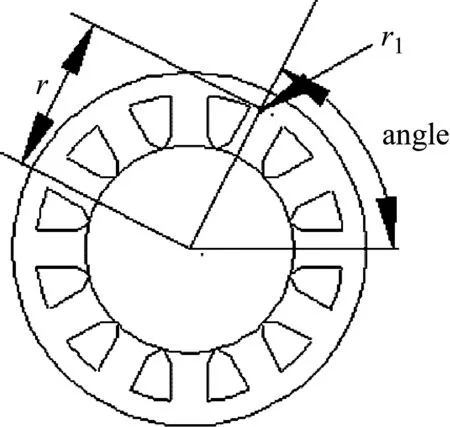
圖4 測量點
然后在COMSOL中進行參數化掃描,對三項數據設定好步長以及掃描范圍,其中r范圍設定為1~3 mm,R范圍設定為55~90 mm,angle范圍設定為0°~90°。對多組填充方案下的電機應力進行有限元參數化掃描計算,然后對每組參數下的應力進行比較,選出最小應力下的填充方案作為最較優填充方案。
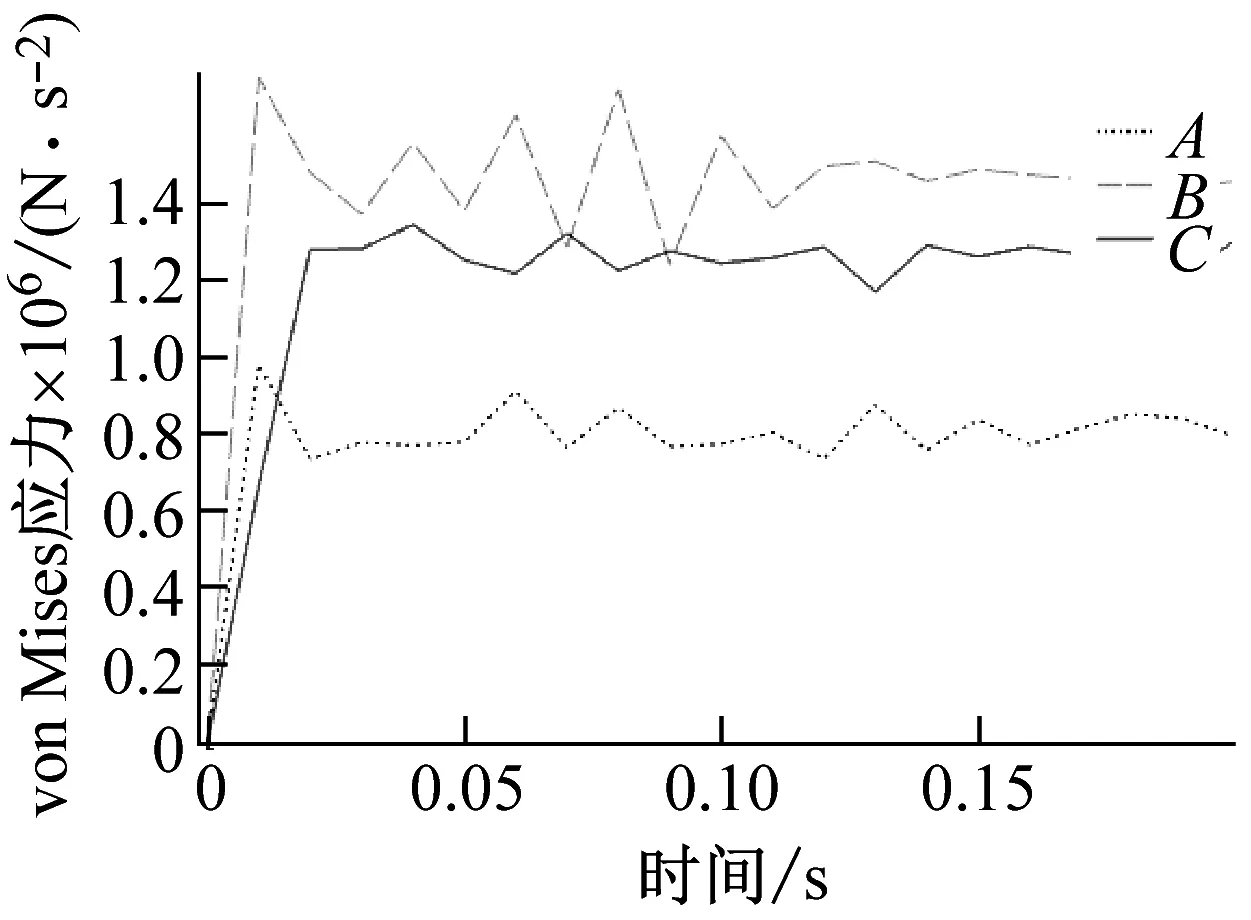
對比圖5和圖6(c),當在孔3處填充負磁致伸縮材料后,點A應力由0.95×106N/m2減小為0.38×106N/m2,減小了60%;點B由1.50×106N/m2變為1.52×106N/m2,點C處應力由1.25×106N/m2改變為1.26×106N/m2,點B和點C應力變化很小。
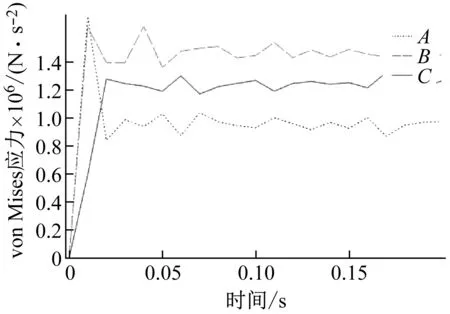
圖5 測量點原應力
(a) 孔1添加Ni
對比圖5和圖6(a),當在孔1填充負磁致伸縮材料后,點A應力由0.95×106N/m2變為0.8×106N/m2,與原應力相比減小了15.7%;點B應力由1.50×106N/m2變為1.52×106N/m2,點C應力由1.25×106N/m2變為1.29×106N/m2,點B和C應力變化很小。
對比圖5和圖6(b)當在孔2填充負磁致伸縮材料后,點A應力變為1.20×106N/m2,與原應力相比增大了26%;點B應力為1.55×106N/m2,點C變為 1.29×106N/m2,點B和C應力在孔2填充負磁致伸縮材料前后變化不大。
由以上三組對比可以發現,打孔填充負磁致伸縮材料后,對填充點附近區域的影響較大,而隨著距離變大后,對較遠距離的影響較小;并且只有在合適的位置打孔并填充負磁致伸縮材料后才會使應力減小,隨意打孔填充負磁致伸縮材料后可能會使應力增大,產生負面影響。
3 試驗結果與分析
根據仿真結果,制定了試驗方案,分別測量了不填充材料和打孔填充負磁致伸縮材料后的電機定子面應力,并選出幾個點對比其填充材料前后的應力變化。
3.1 試驗儀器與準備
如圖7所示,本試驗采用的為三片直角型應變片,可以對測量位置的0°、45°、90°三個方向進行應變測量。

圖7 應變片
本文根據仿真思路設計了試驗裝置,如圖8所示,去掉一個永磁同步電機的轉子,這樣磁通主要集中約束在定子鐵心內部,外部氣隙中的漏磁通很小,定子齒表面的電磁力很小,定子鐵心的主要應力為磁致伸縮力。

圖8 電機定子
在電機4個位置粘貼應變片,并分別命名為A、B、C、D,應變片A和B周圍沒有孔,C右側為直徑4 mm孔,D左右兩側都有4 mm孔。從左到右分別為編號1、2、3、4、5、6的直徑4 mm孔。其中孔1為添加負磁致伸縮材料的適合位置之一。
圖9中利用變頻器給電機繞組中通入50 Hz的工頻電產生交變旋轉磁場,利用JHDY 動態應變測量系統測量電機定子上應變片粘貼位置的應變,采樣頻率設定為1 000 Hz,在電機定子線圈未通電時對數據進行調零,消除環境的影響,再通電進行測量。每次改變硅鋼片片數后通電測量前都要重新調零。之后將數據在電腦中進行保存。

圖9 電機應變測量裝置
3.2 孔1添加鎳后對應變片B和C的影響
圖10中兩圖為應變片B在孔1打孔填充負磁致伸縮材料前后的應變對比。孔1添加負磁致伸縮材料鎳后應變峰值由165.913 με變為了163.217 με,變化量為1.6%,谷值由-111.283 με變為-108.878 με,變化量為2.1%。由于孔1與應變片B距離較遠,大約70°,所以變化量很小,與仿真規律相同。
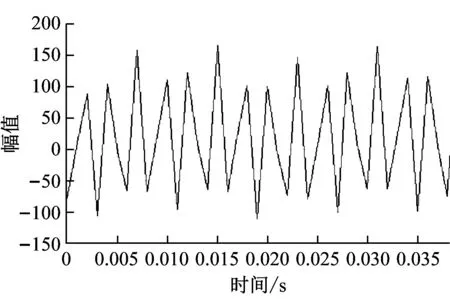
(a) 添加材料前B應變
圖11(a)、(b)、(c)三圖分別為應變片C在未添加負磁致伸縮材料時、僅孔1填加Ni時、孔1和4添加Ni時的應變對比。孔4與應變片C相差約43.6°、孔5與應變片C相差約60°,兩孔都距離應變片C較遠;而孔1緊挨著應變片C,距離非常近。
圖11(a)和圖11(b)對比,發現當在孔1填充負磁致伸縮材料后,應變片C峰值由148.424 με減小為124.110 με,應變峰值減小了16%;圖11(b)和圖11(c)對比,應變峰值由124.110 με變為124.054 με,峰值變化量為0.05%;谷值由-96.699 με變為-90.659 με,變化量為6.2%,總體考慮誤差后變化較小。已知孔4距離應變片C較遠,而孔1距離應變片C較近,所以孔1填充負磁致伸縮材料后對應變片C的影響較大,而孔4填充負磁致伸縮材料則影響較小。
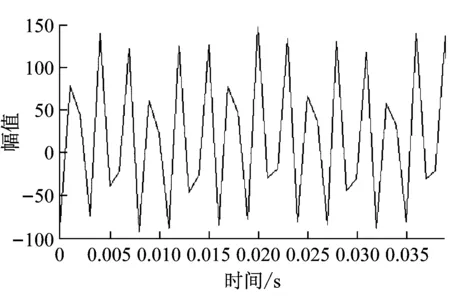
(a) 添加材料前C應變
3.3 孔1添加鎳后應變片B、C、D應變對比
圖12為應變片D在孔1添加Ni后的應變,結合圖10(b)孔1添加Ni后B應變圖,和圖11(b)孔1添加Ni后C應變圖。發現應變片C的應變峰值為124.110 με,遠小于應變片B的163.217 με和D的179.540 με。可知應變片C距離孔1較近,而且孔1未添加Ni時與僅孔1添加Ni時應變片C最大應變減小了16%。
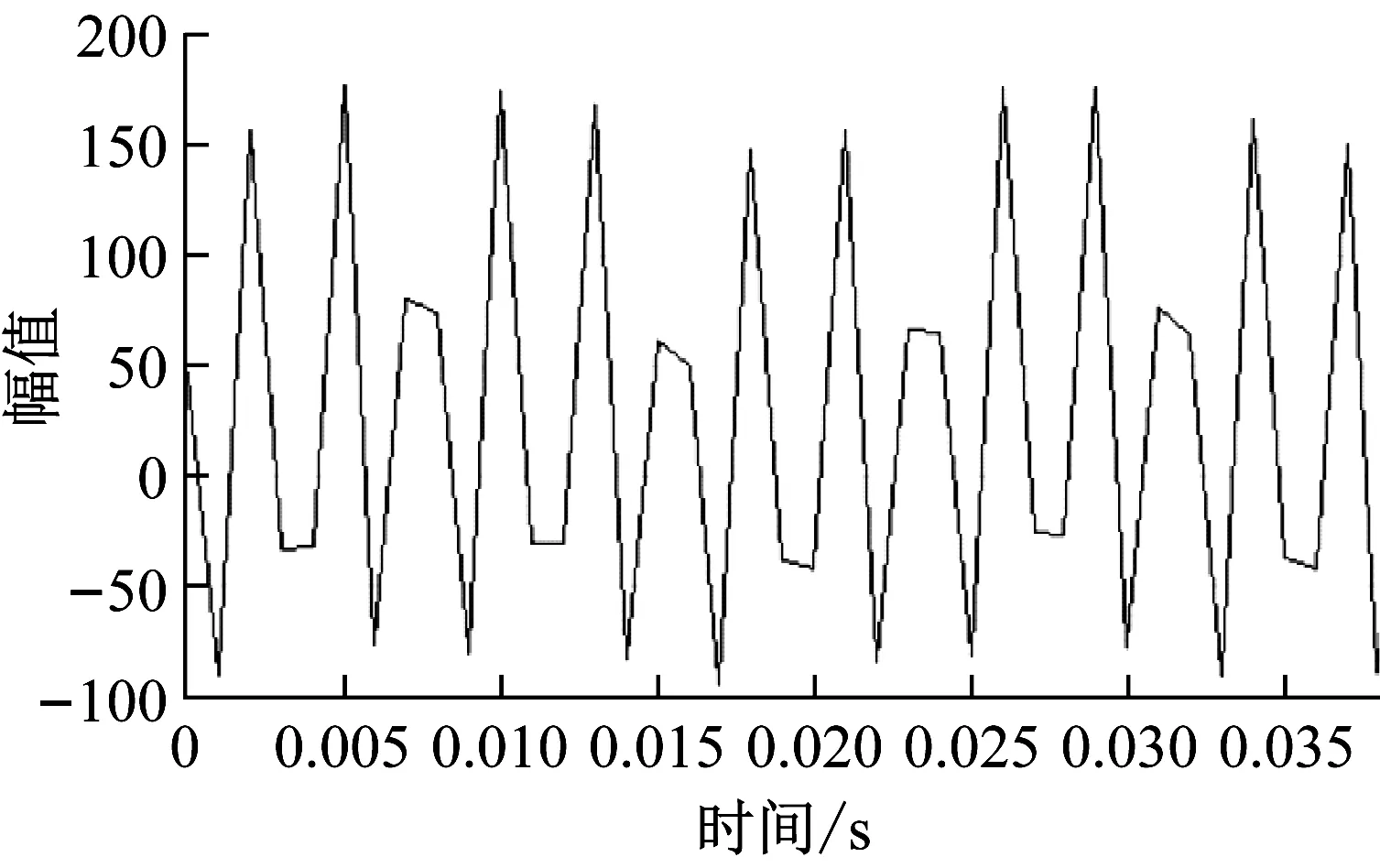
圖12 孔1添加Ni后D應變
以上對比可發現當在電機定子合適的位置填充負磁致伸縮材料后,可以使填充材料附近的應變減小。磁致伸縮效應會使電機定子伴隨電源頻率產生規律性的伸長和縮短,從而引起電機本身的振動和內部應力,同時硅鋼片表面的伸長和縮短正是應變的來源,所以說應變量減小了,對應的內部應力也會減小,從而電機的振動噪聲也就減小了。
還可發現打孔填充負磁致伸縮材料后對填充材料位置附近區域的影響較大,而距離填充負磁致伸縮材料位置較遠的區域,則影響較小。這是因為所填入負磁致伸縮材料產生的形變改變了電機定子內部的應力,而由形變產生的內部應力又是隨著距離增大而遞減的,所以隨著測量點與填充位置處距離的增大,測量點的應變所受到的影響也就越小。
4 結 論
本文首先建立了永磁同步電機的磁-機械耦合數值模型,在有限元中對電機定子應力進行了系統的分析。并根據仿真模型制作真實的電機模型,進行電機定子打孔填充負磁致伸縮材料的仿真試驗進行驗證,試驗結果與仿真基本相符。得出結論如下:
(1) 根據擬填充負磁致伸縮材料的特性找到合適的打孔填充位置和尺寸,然后在電機定子上打孔并填充負磁致伸縮材料,可以使電機定子的應變和面應力減小,從而達到減振降噪的目的。
(2) 在電機定子上打孔填充負磁致伸縮材料后,會使定子的面應力發生變化,而應力改變的幅度與測量點到填充位置處的距離成反比。距離越近,應力變化的幅度越大;距離越遠,應力變化的幅度越小。本試驗驗證了局部應力的變化情況,在電機其他定子齒對稱位置同樣打孔填加材料可以減小電機定子整體應力。
此結論對低噪聲永磁同步電機的設計有重要的參考價值。

