基于BP-MOPSO 的散貨船艙口圓形角隅疲勞強度優化設計

李 鵬 韓曉劍 秦洪德 鄧忠超

（哈爾濱工程大學 船舶工程學院 哈爾濱 150001）

0 引 言

為了在散貨船上獲得更多的使用空間以提高利潤，同時也方便貨物裝卸，散貨船甲板上的貨艙開口通常比較大，但由此其結構連續性便遭到破壞，不利于應力傳遞，極易形成應力集中，這使得艙口角隅的疲勞問題尤為嚴重。鑒于散貨船在海運中無法替代的重要作用，散貨船艙口角隅疲勞強度的優化是一個很有意義的研究問題。散貨船甲板艙口角隅處的應力集中主要受以下因素影響：艙口寬度與整個船寬的比值、艙口長寬比、艙口角隅處的形狀，其中角隅的幾何形狀對應力集中系數影響最大。

目前針對艙口角隅的優化思想主要分為2 種：一種是增加板厚，另一種就是改變角隅結構型式。倪敏杰根據CCS 規范對某超大型集裝箱船艙口角隅的直角角隅、半圓形負半徑角隅及新型角隅結構的疲勞強度進行了分析對比，得出一種較適宜的超大型集裝箱船艙口角隅結構形式。陳景昊根據ABS、NK 和CCS 的疲勞規范的有關規定和建議，通過比較幾種角隅形式疲勞壽命的方式對艙口角隅的結構形式進行了優化設計。樊祥棟等分析了CSR BC &OT 共同規范中的新規定，按照新規對某單殼散貨船的甲板艙口角隅及縱向艙口圍板趾端的疲勞強度評估及結構形式的多方案比較優化，認為近似圓弧形的角隅比拋物線型角隅在抵抗斜浪扭矩方面更有優勢。以上工作均是基于上述兩種優化思想，問題在于其只對有限種角隅形式進行了分析，未進行連續性的分析。孫力首次將BP 神經網絡和MOPSO 尋優算法結合引入到超大型集裝箱船的角隅疲勞優化中，以ANSYS 的子模型法提供大量子模型數據支持BP 神經網絡的訓練，模擬角隅應力及重量和結構參數間的連續非線性關系。

本文以1艘174 000載重噸散貨船為實船算例，依據CCS《船體結構疲勞強度指南》（2018）對 6 號艙室艙口角隅的疲勞壽命進行計算，并基于BP-MOPSO 算法，設計了子模型法和全局模型法，從提高疲勞壽命和減輕結構重量的角度對比兩種方法，對散貨船的艙口角隅進行了優化，分析圓形角隅的結構參數對疲勞壽命的影響，得到一組較優的角隅結構形式。

1 有限元模型建立及角隅疲勞校核

1.1 三艙段有限元模型

目標散貨船主要參數如表1 所示。

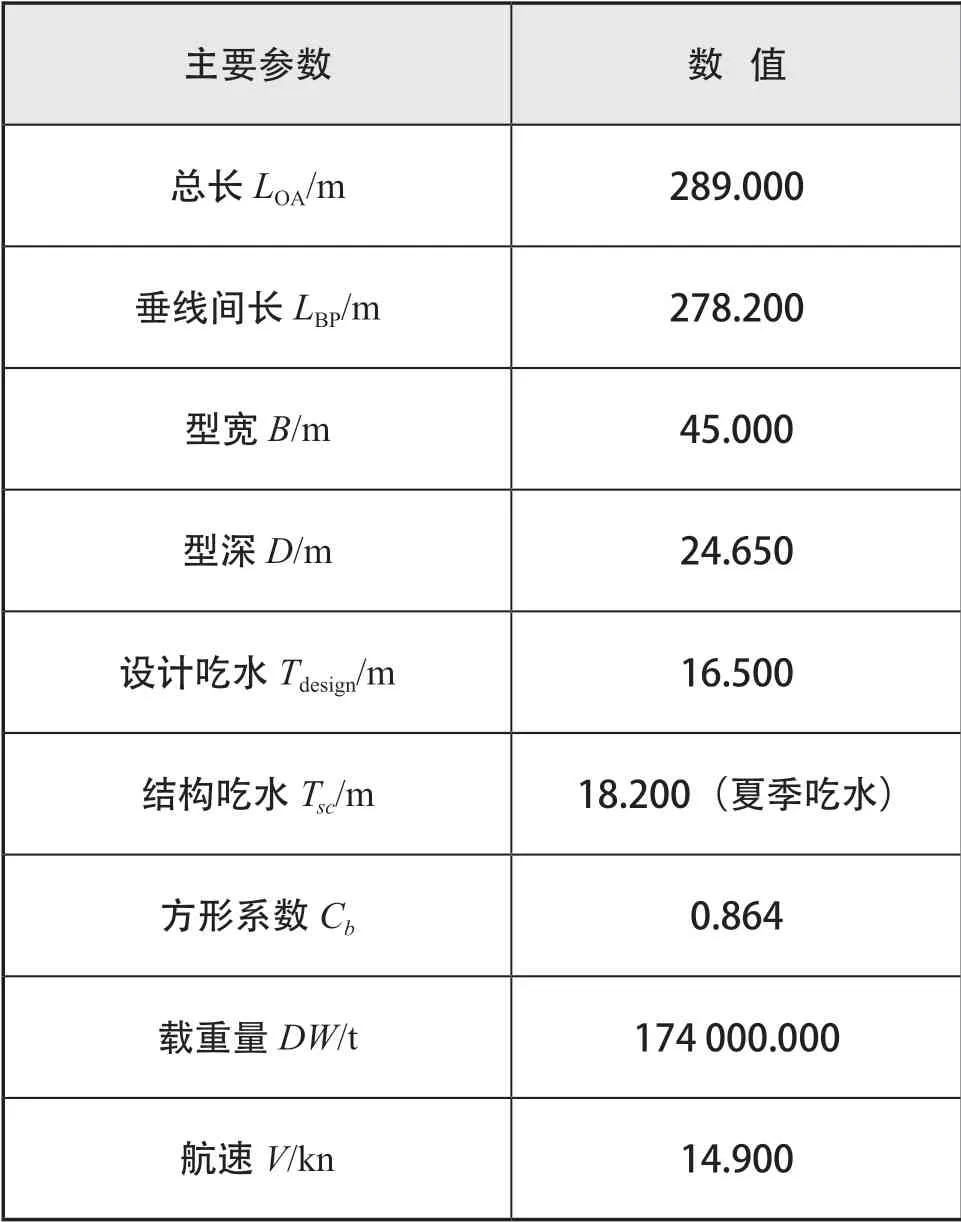
表1 散貨船主要參數

依據CCS《船體結構疲勞強度指南》（2018）5.2 節中的規定建立三艙段有限元模型如下頁圖1所示，艙口角隅的精細化模型如下頁圖2 所示。原船舶角隅無過渡結構，先增設半徑為1 m、板厚為 36 mm 的初始圓角過渡結構。

圖1 三艙段有限元模型

圖2 角隅精細化模型

1.2 初始角隅壽命計算

結合該散貨船的裝載手冊，選取均勻滿載、兩端裝載、中間裝載和正常壓載4 種裝載工況，以及中拱迎浪、中拱隨浪、中垂迎浪和中垂隨浪4 種載荷工況，共組合出16 種計算工況。

根據CCS 疲勞指南將相應的總體載荷和局部載荷施加于有限元模型后，計算處理得到6 號艙室艙口4 個角隅的疲勞壽命。根據角隅直角頂點的坐標不同為角隅編號，即：角隅1（119.39 m，-10 m，25.34 m）；角隅2（119.39 m，10 m，25.34 m）；角隅3（113.86 m，10 m，25.34 m）；角隅4（113.86 m，-10 m，25.34 m）。各角隅疲勞壽命如表2 所示。

表2 初始角隅累計損傷度及疲勞壽命

由表2 可見：1 號角隅的疲勞問題比較嚴重，未能滿足規范的20 A 壽命要求；2 號角隅接近滿足；其他角隅均滿足。

2 BP 神經網絡和MOPSO 算法簡述

2.1 BP神經網絡

優化艙口角隅時，需建立艙口角隅應力和疲勞壽命與角隅的結構參數間非線性關系的代理模型。BP 神經網絡（Error Back Propagation Neural Network）正以很強的非線性逼近及學習訓練能力聞名，適用于模擬這種非線性關系。HORNIK K 等于1939 年在數學上已經證明具有單S 型隱含層和單線性輸出層的BP 神經網絡可以逼近任意非線性系統，故神經網絡隱含層一般設為1 層。

本文采用平均相對變動值（ARV）來評估BP神經網絡的預測效果。ARV 值越小，則BP 神經網絡的訓練效果越好。

2.2 MOPSO算法

本文對艙口角隅的優化包含角隅重量及角隅疲勞壽命或角隅應力多個目標函數，屬于多目標優化的問題，而多目標粒子群優化算法（Multi-Objective Particle Swarm Optimization，MOPSO）正應此而生。MOPSO 算法由粒子群算法（PSO）改進而來，COELLO C 等于2004 年提出了具有里程碑意義的MOPSO。KENNEDY J等于1995年提出了PSO算法。PSO的基本思路是模擬自然界中鳥群搜尋食物的過程來找到單目標優化的最優解，通過計算機程序模擬種群中的個體與群體，具有原理簡單、收斂迅速等優點。

3 艙口角隅優化

3.1 子模型法

子模型法是通過拉丁超立方抽樣法（Latin Hypercube Sampling，LHS）獲得設計變量的樣本空間，以BP 神經網絡模擬角隅應力和設計變量之間的非線性關系，易得角隅重量與設計變量的函數關系；以MOPSO 算法進行艙口角隅優化設計，將Pareto 前沿中的數據歸一化處理后，采用包含權重的最小距離法，從非劣解集中得到一組最優解。

3.1.1 子模型建立

本文旨在對圓形角隅的疲勞強度進行探究，故設計變量為角隅半徑/mm 及板厚/mm。設計變量取值范圍見表3 所示。

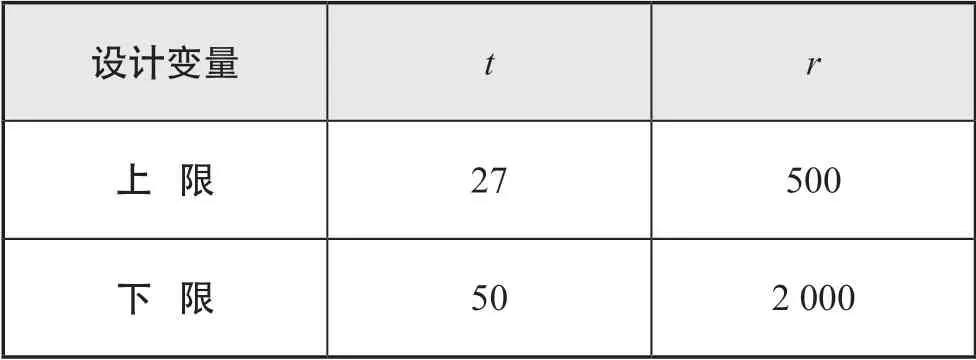
表3 設計變量的取值范圍mm

前人一般使用ANSYS 中的子模型法，本文探索出一種使用Patran 建立大量子模型的方法。以1.2 節中的角隅形式為基礎，考慮到1 號角隅壽命最短，將其在另一模型數據庫中重新參數化建立，即為子模型。由1.2 節中的結果數據可知，均勻滿載中拱時熱點合成應力最大，故以此工況下角隅邊界節點的位移作為強制位移施加于子模型中。為驗證初始子模型的正確性，首先對比原模型和子模型中1 號角隅的位移等值線圖（如圖3 和 圖4 所示），可見兩者之間的趨勢和大小基本一致；然后對比兩者的Von Mises 應力云圖（如下頁圖5和圖6 所示），其角隅自由邊最大應力相差0.25%，兩者之間的趨勢及大小基本一致。由此，子模型的正確性得到驗證。

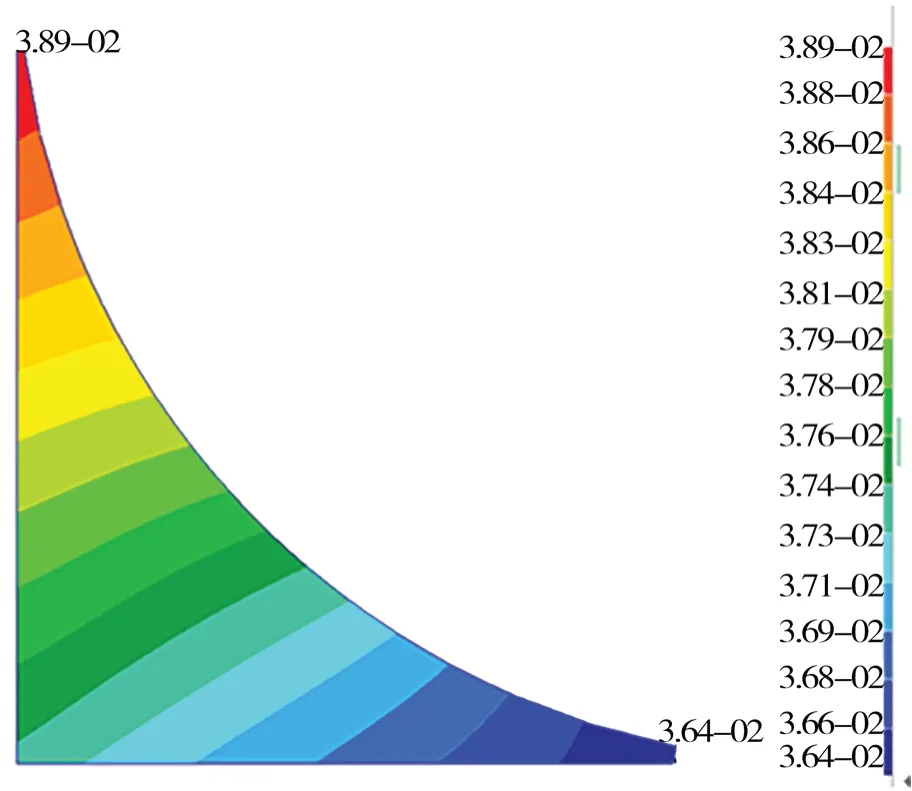
圖3 原模型中角隅1 位移云圖

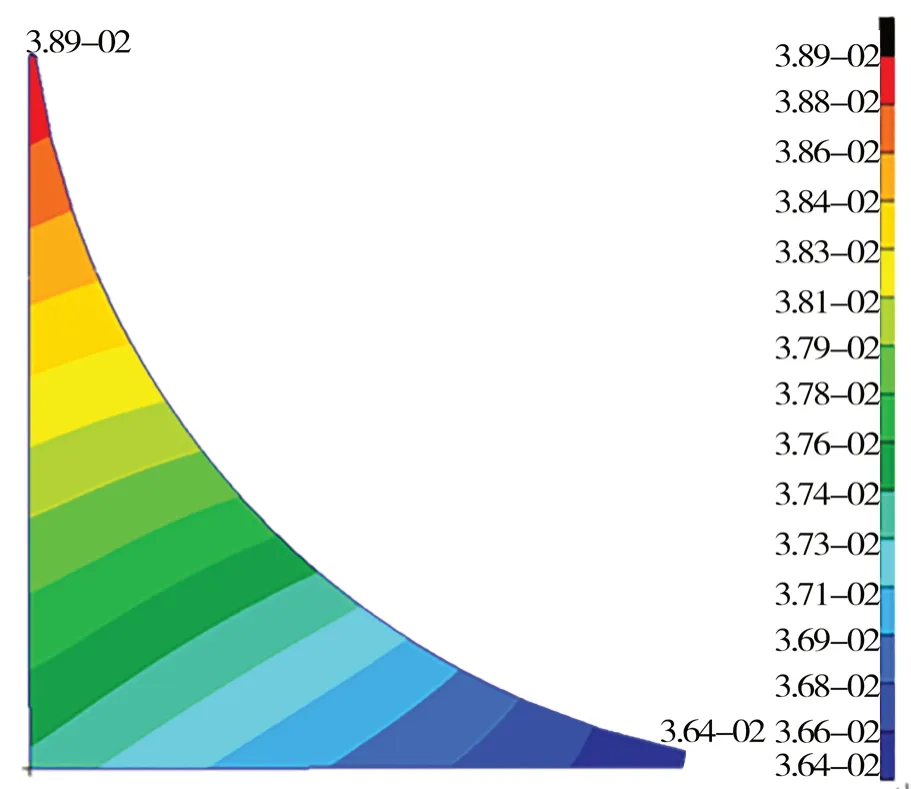
圖4 子模型中角隅1 位移云圖

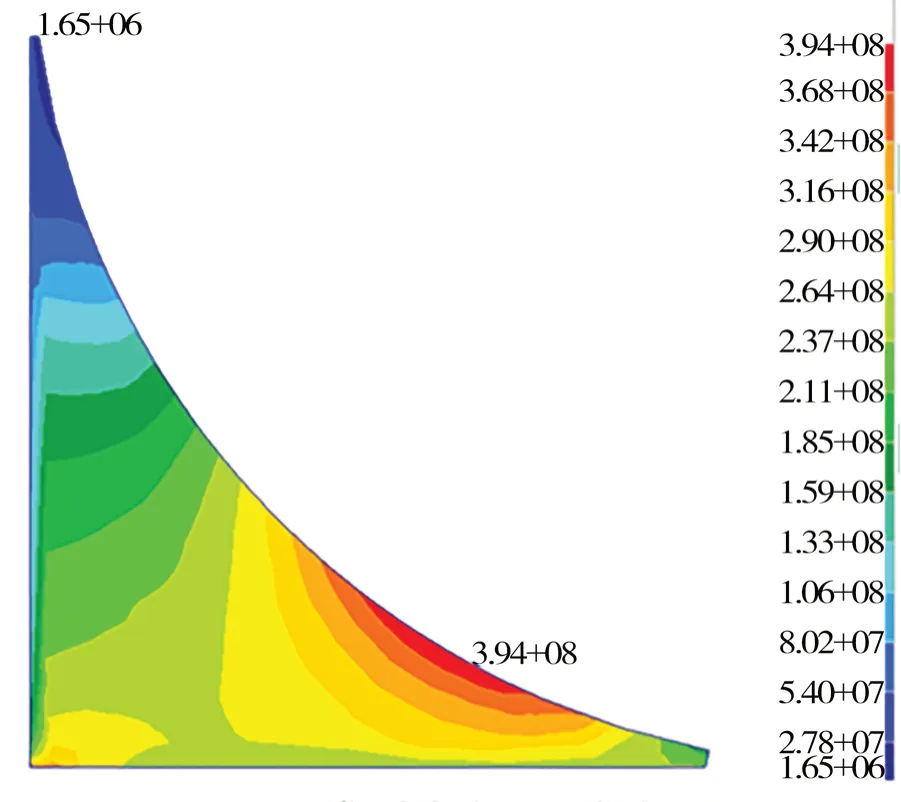
圖5 原模型中角隅1 應力云圖

圖6 子模型中角隅1 應力云圖

為得到訓練BP 神經網絡的大量數據，通過Patran 中Group 功能將子模型大量生成在子模型空間中，變換參數由LHS 抽樣獲得；通過PCL 函數，將LHS 抽樣中的板厚賦給對應角隅。由于每當角隅結構形式發生變化時，其邊界節點位移即發生變化。考慮到角隅周圍艙口的結構剛度度強于角隅，認為邊界節點的位移變化不大具有一定合理性。為方便設置，此處假定邊界條件不變，以半徑1 m、厚度36 mm 角隅的角隅邊界節點的位移作為強制位移施加于不同子模型中。

3.1.2 訓練BP 神經網絡

首先，使用LHS 抽樣獲得3 組設計變量，第1、2、3 組分別有500、1 000、2 000 個樣本數據。在Patran 中各自參數化建模計算后，得到對應的應力云圖，圖7 為第2 組部分角隅的應力云圖。然后以角隅半徑、板厚作為輸入層，提取各角隅155 號單元的中心點應力作為輸出層，每組各取15%數據作為測試集，神經網絡隱含層設為1 層。采用梯度下降法進行訓練，訓練次數設為1 000，學習速率設為0.01，訓練目標最小誤差設為1×10。經多次試驗，將隱含層節點數設為10。建立一個2-10-1網絡結構。

圖7 第2 組部分角隅的應力云圖

各組訓練樣本的訓練結果如表4 所示，由平均相對變動值（ARV）對比，選擇訓練樣本個數為 1 000時訓練的網絡作為接下來優化算法的目標函數。

表4 各訓練樣本的訓練結果

3.1.3 MOPSO 算法優化

子模型法中，艙口角隅的多目標優化數學模型如下：

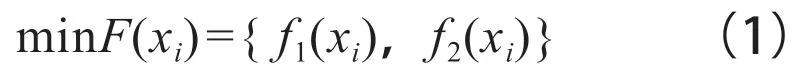
式中：()為單個艙口角隅的重量，kg；(x)為3.1.2節中訓練得到的BP神經網絡。顯然：

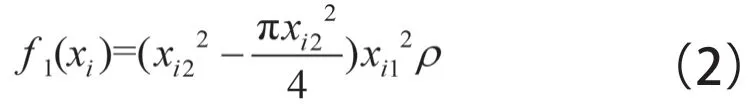
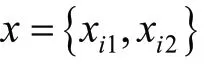
式中：為板厚，mm；為角隅半徑，mm；為材料密度，kg/mm。

MOPSO 中的參數設置為：粒子群大小為100，外部檔案大小為100，最大迭代次數為200，權重系數為0.4，學習因子1 與2 均為2，變異率為0.1。BP-MOPSO 優化得到的Pareto 前沿面如圖8 所示。

圖8 子模型優化得到的Pareto 前沿面

由于應力和重量之間的數值差距較大，為保證兩個函數在未加入權重參數前對最小距離的貢獻一致，消除兩組目標函數結果本身數值上的較大差異對最小距離的影響，見式（3）和式（4）。

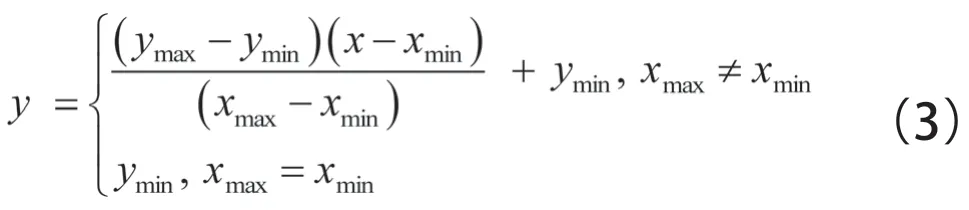
式中：為歸一化的上限；為歸一化的下限；為數據的最大值；為數據的最小值。

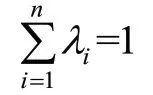
將兩組數據使用式（3）所述映射將數據歸一化到0，1 之間。最后，按式（4）采用含有權重的最小距離法從Pareto 前沿面中選取最優結果，表5為不同權重下設計變量的優化結果，優化后BP 神經網絡的預測值與有限元計算結果的誤差對比如表6 所示。

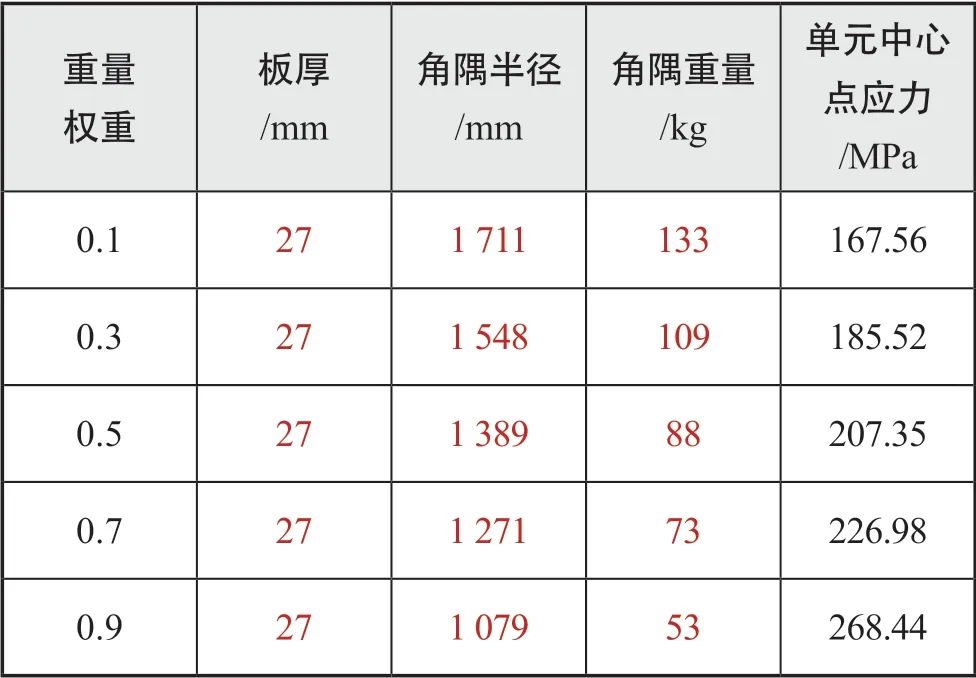
表5 不同重量權重下設計變量的優化結果

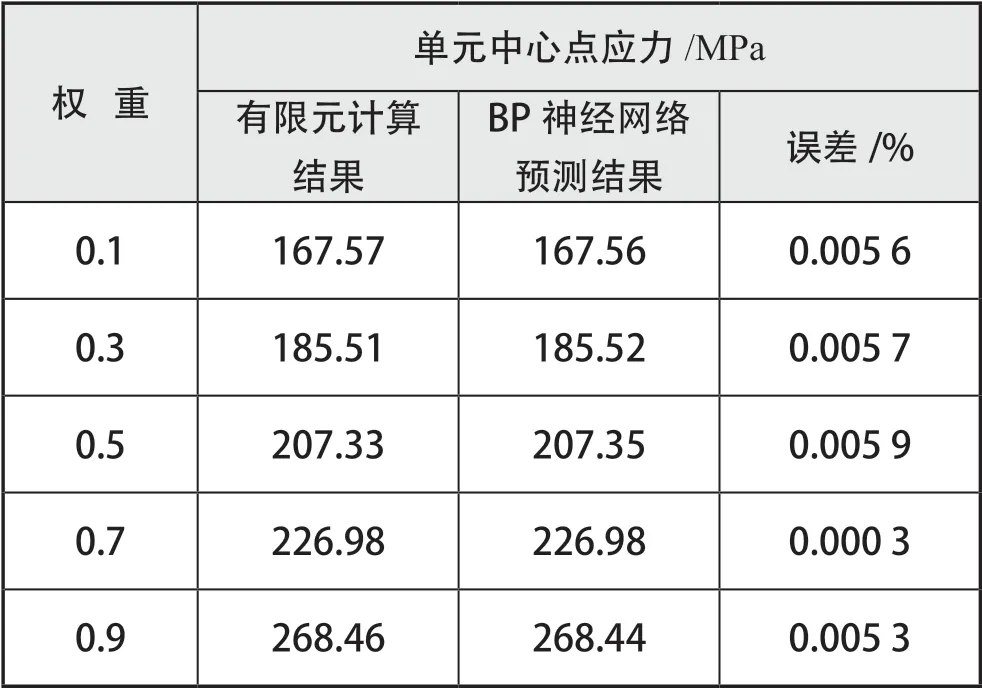
表6 BP 神經網絡預測值與有限元計算結果的誤差對比

誤差最大為0.005 9%，在允許范圍內，因此認為BP 神經網絡預測準確。

考慮到相對于整體船舶質量，該處結構重量所占比例較小，取=0.1 和=0.9 時的設計變量在全局模型中對角隅進行修改，與1.2 節中初步設計的角隅對比如下頁表7 所示。相比原結構，=0.1 時，角隅重量增加了119.54%，壽命提升了19.25%；=0.9 時，角隅重量減少了15.66%，壽命減少了7.60%。可見，減輕角隅重量與提升角隅疲勞壽命之間矛盾很深，除非大幅度增加角隅重量，疲勞壽命很難有較大提升。

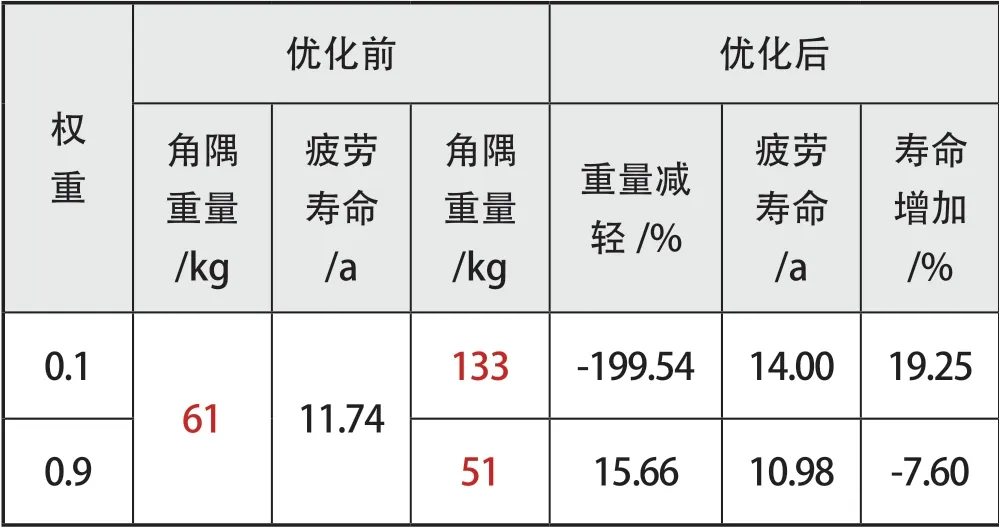
表7 權重對優化的影響及優化前后對比

3.2 全局模型法

全局模型法即直接在原模型中修改角隅結構形式，計算角隅的疲勞壽命。

3.2.1 全局模型建立

由表3 中的設計變量取值范圍，計算了30 種角隅的結構形式在角隅1 處的疲勞壽命，參見表8；定義了一個評價參數壽命重量比用于評估不同形式的角隅，顯然其值越小表明角隅越優秀。疲勞壽命隨角隅半徑和板厚的變化如下頁圖9 所示。當板厚一定時，隨角隅半徑的增加，疲勞壽命的增加趨于平緩；當角隅半徑一定時，隨板厚的增加，疲勞壽命的增加同樣趨于平緩。壽命重量比隨角隅重量和疲勞壽命的變化如下頁圖10 所示。隨角隅重量的增加，疲勞壽命的增加越來越平緩，壽命重量比逐漸下降，即單位結構重量對疲勞壽命的貢獻越來越低，見式（5）。

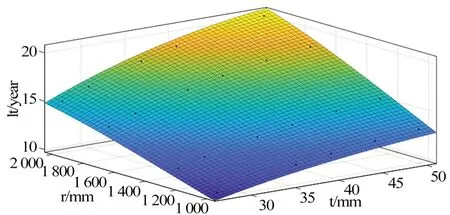
圖9 疲勞壽命隨角隅半徑和板厚的變化

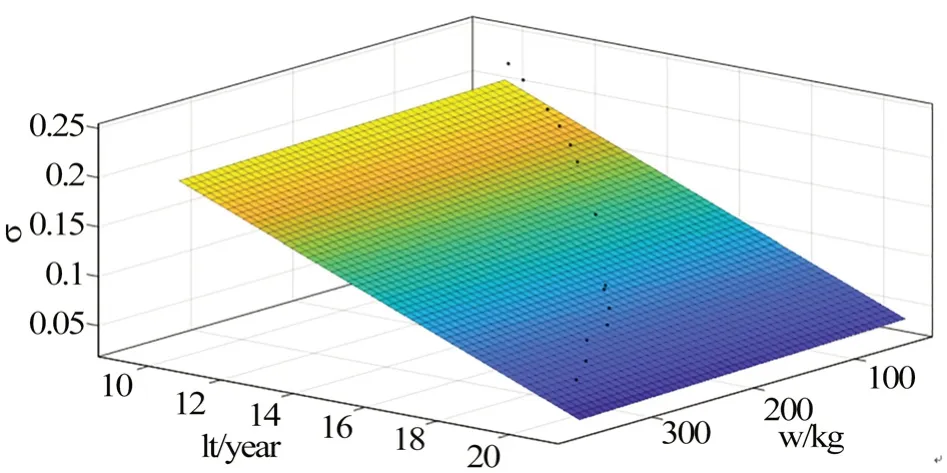
圖10 壽命重量比隨角隅重量和疲勞壽命的變化

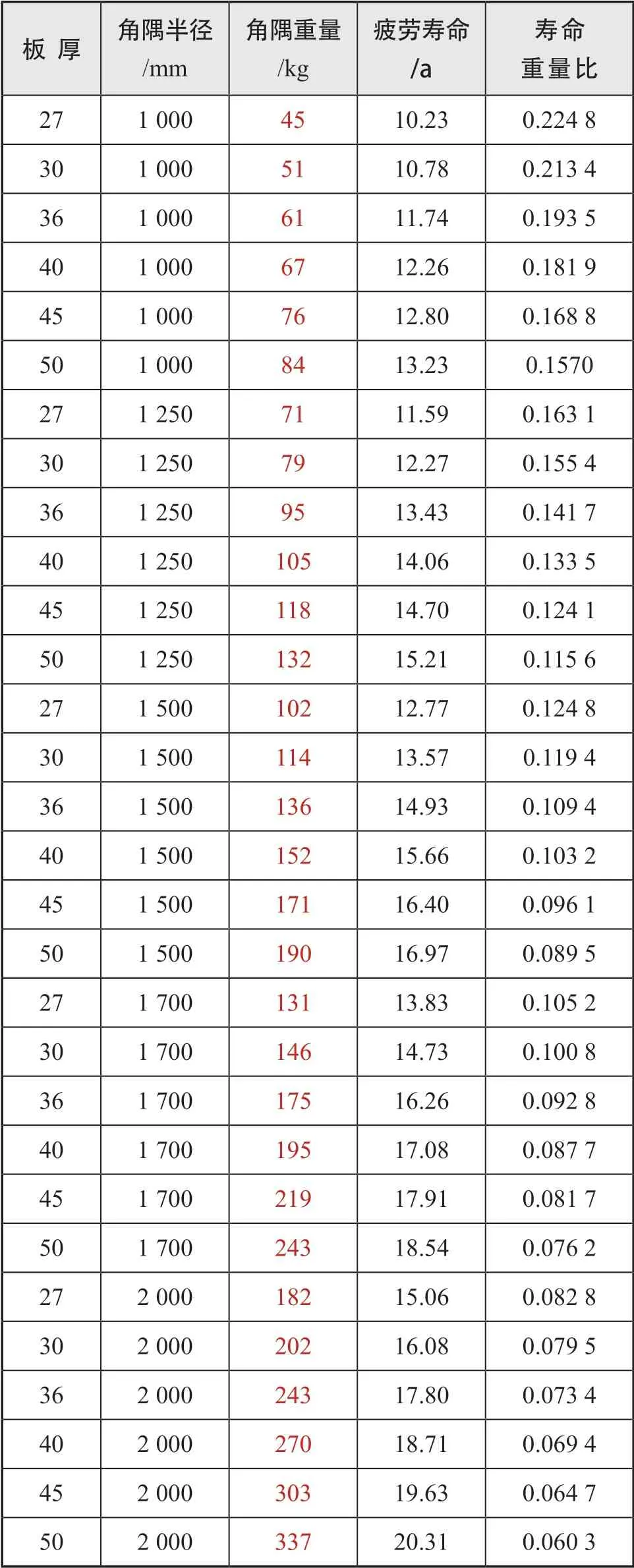
表8 30種角隅的參數及疲勞壽命

式中：為角隅1的疲勞壽命，a；為角隅重量，kg。

3.2.2 訓練BP 神經網絡

使用表8 中的數據，同3.1.2 中的方法，將輸出層改為疲勞壽命。由于數據較少，將全部數據作為測試集，經多次實驗，隱含層節點設為6，其余參數與3.1.2 中相同。由此建立一個2-6-1 網絡結構。訓練結束后，平均相對變動值ARV=4.14×10。

3.2.3 MOPSO 算法優化

全局模型法中，艙口角隅的多目標優化數學模型如下：

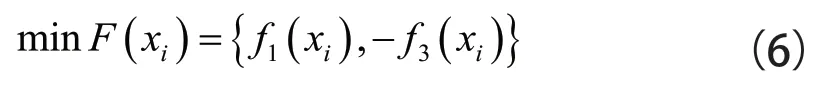
式中：(x)為根據3.2.2 節中訓練得到的BP 神經網絡；疲勞壽命與設計變量之間均為正相關關系，故添加負號，使MOPSO優化時()向最小值優化，()向最大值優化。

設計變量范圍與MOPSO 參數設置同3.1.3 節。最終優化得到的Pareto 前沿面如圖11 所示。

圖11 全局模型優化得到的Pareto 前沿面

表9為不同重量權重下設計變量的優化結果。結果中，角隅1疲勞壽命BP神經網絡的預測值與有限元計算結果的誤差對比見下頁表10。最大誤差值為0.030 2%，在可接受范圍，認為BP神經網絡預測準確。

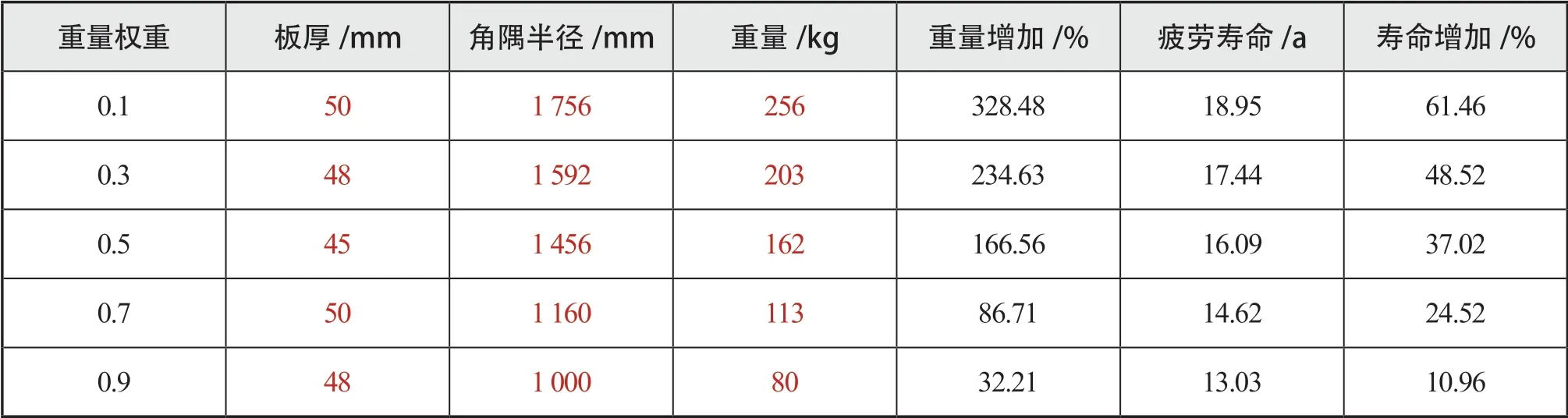
表9 不同重量權重下設計變量的優化結果

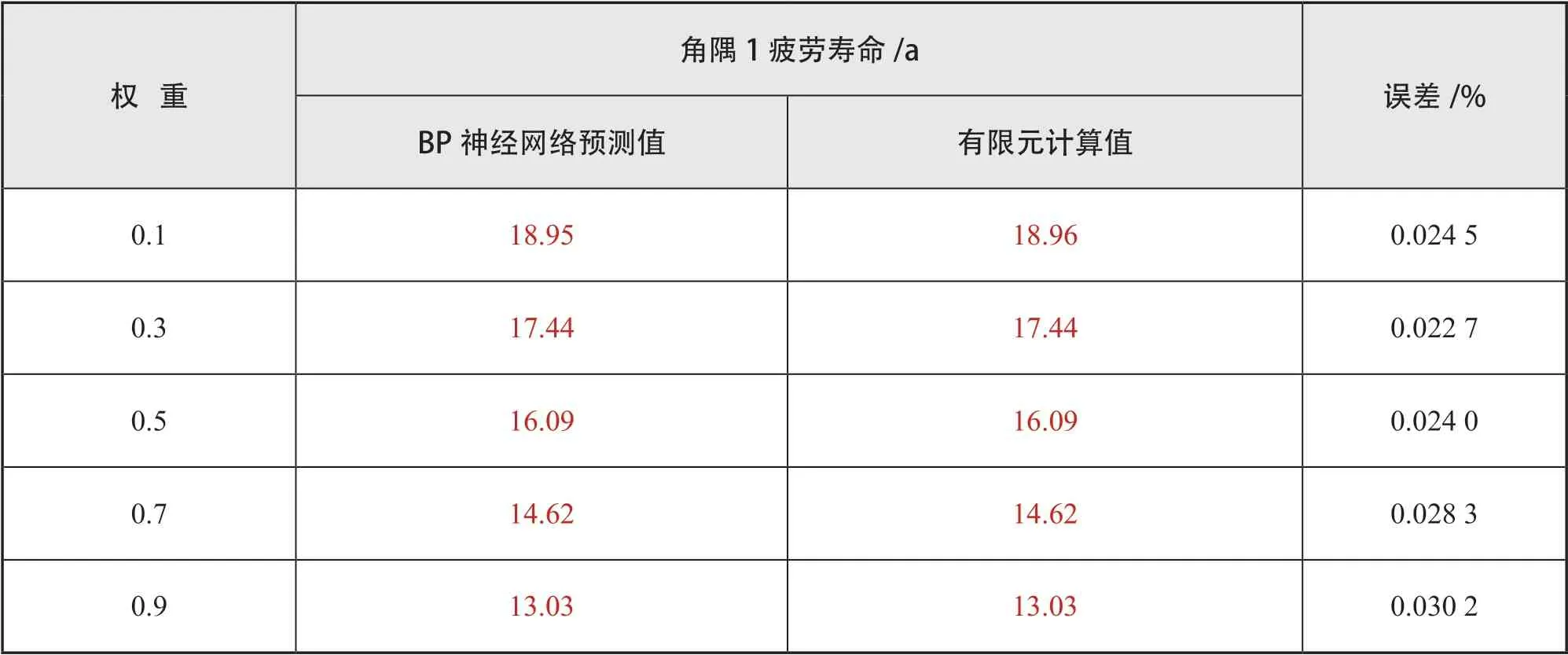
表10 BP 神經網絡預測值與有限元計算結果的誤差對比

3.3 兩種方法的對比分析

3.3.1 子模型法優缺點

子模型法的優點在于能夠獲取大量原始數據訓練BP 神經網絡，手工操作工作量相對較少，可以保證BP 神經網絡預測值的精確性。缺點在于子模型的邊界節點的位移約束條件是基于假定而來的，對板厚這一設計變量敏感度不高，未能反應板厚變化對應力的影響；不能直接用BP 神經網絡擬合角隅疲勞壽命與角隅結構參數之間的非線性關系，只能用某一對疲勞損傷度影響較大的計算工況下的應力來反映壽命。

3.3.2 全局模型法優缺點

全局模型法的優點在于更直接地反映了角隅結構參數的變化對疲勞壽命的影響，通過訓練BP神經網絡獲得了角隅結構參數和疲勞壽命之間的非線性關系，較為直觀；對兩個設計變量對疲勞壽命的影響反應均較好。缺點在于用來訓練的原始數據較少，無法通過比較評估參數選擇更優秀的BP 神經網絡，可能會導致BP 神經網絡準確度不足，但由實際對比可知其仍誤差均較小，原因可能是訓練BP 神經網絡時所取的設計變量范圍較小，30 組數據足夠BP 神經網絡模擬，且在MOPSO 調用BP 神經網絡時，未超出訓練時的變量范圍，因此即使網絡的泛化性不好對預測結果也沒有影響；同時手工操作工作量較大，角隅處的有限元模型及網格細化一般均需手工建立。

綜上所述，認為全局模型法優化結果的置信度更高。以全局模型法的優化結果為準，得到一組考慮重量權重的最優解，如上頁表9所示。

4 結 論

本文主要研究了BP 和MOPSO 算法在散貨船圓形艙口角隅疲勞強度優化方面的應用，基于BPMOPSO 算法設計了兩種優化方法，得出以下結論：

（1）BP 神經網絡可以用于模擬角隅結構參數和應力及疲勞壽命之間的非線性關系，其精度足以滿足要求，可大大縮減有限元計算耗費的時間，提高效率；

（2）在前人提出的包含權重的最小距離法基礎上作進一步改進，對MOPSO 優化后Pareto 前沿的數據歸一化處理，可消除兩組目標函數結果本身數值上的較大差異對最小距離的影響，使得包含權重的最小距離法得到的最終優化結果數據分布更合理；

（3）探究出一種在Patran 中批量建立子模型的方法；

（4）提出以壽命重量比的概念評估角隅重量對疲勞壽命的貢獻；

（5）對于圓形角隅結構而言，在本文所取的設計變量取值范圍內，角隅重量和疲勞壽命之間保持了正相關關系，這表明對于圓形角隅結構，很難在減少重量的同時提高疲勞壽命。