基于新型軸向電渦流阻尼器的拉索多模態減振性能研究

肖 瀟， 黃智文， 陳政清， 華旭剛

(1. 湖南大學 風工程與橋梁工程省重點實驗室，長沙 410082；2. 湖南大學 振動與沖擊技術研究中心，長沙 410082)

斜拉索具有自振頻率低、固有阻尼小等特點，極易發生風雨振、渦振和參數共振等振動病害[1]。理論研究和工程實踐表明，安裝索端阻尼器是減小各類拉索振動病害的有效措施[2-3]。按阻尼特性來分，目前使用最廣泛的索端阻尼器主要有線性黏滯阻尼器和磁流變阻尼器。前者采用被動控制策略，能給中等長度的拉索提供足夠的附加阻尼，有效抑制拉索振動。然而，千米級斜拉橋的拉索長度超過500 m, 其多個模態都有發生大幅振動的可能，因此要求索端阻尼器能為拉索的多個模態都提供足夠的附加阻尼。線性黏滯阻尼器可為拉索提供的最大附加模態阻尼比僅由其安裝高度決定，且阻尼器的最優阻尼系數與拉索的模態階次成反比[4-7]。隨著拉索長度的不斷增大，阻尼器的相對安裝高度也不斷減小，線性黏滯阻尼器也就越難同時為拉索多個模態提供足夠的附加阻尼；另一方面，磁流變阻尼器的阻尼系數可以由輸入電流的大小來調節，從而可以通過利用半主動控制算法對拉索多個模態實現最優控制[8-10]。然而，基于半主動控制算法的磁流變阻尼器需要有穩定的電源供應，還要防止因磁流變液沉淀而導致的性能退化[11]。

近年來，基于負剛度阻尼器和慣質的拉索被動耗能減振理論受到關注[12-14]。在保持拉索安裝高度不變的條件下，在線性黏滯阻尼器系統中引入負剛度或慣質，都可以顯著提高阻尼器系統對拉索單個模態的減振效果。然而相比單模態控制，引入負剛度或慣質對提升拉索多模態的減振效果并沒有那么顯著。一個重要的原因在于引入了負剛度或慣質后，減振系統中線性黏滯阻尼器的最優阻尼系數仍然與拉索模態階次相關，因此難以實現多個模態的最優控制[15]。

除線性黏滯阻尼器外，指數型液體黏滯阻尼器和摩擦阻尼器等非線性阻尼器的拉索減振效果也受到一些學者的關注。Main等[16]基于單位周期內非線性阻尼力與拉索張力之間的不平衡力均方差最小的原則，推導了指數型液體黏滯阻尼器最優阻尼系數的解析表達式，并發現當阻尼器的速度指數α=0.5時，其最優阻尼系數與拉索模態階次無關。Krenk等[17]利用非線性阻尼器在一個周期內耗能與線性阻尼器相等的原則，推導了分數階阻尼力模型和指數型液體黏滯阻尼器的最優阻尼系數表達式。基于Krenk等提出的上述等效線性方法，Hoang等[18]分析了摩擦阻尼器和雙折線阻尼器等非線性阻尼器的拉索減振效果，并發現通過合理的參數設計，可以使各階模態對應的最優阻尼器參數較為接近，從而達到比線性阻尼器更好的多模態減振效果。周海俊等[19]和王慧萍等[20]分別通過試驗和有限元分析發現摩擦阻尼器可提供的最大附加模態阻尼比大于線性黏滯阻尼器，且附加模態阻尼比具有振幅依賴性。Chen等[21]提出了采用諧波平衡法分析安裝有指數型液體黏滯阻尼器和摩擦阻尼器的斜拉索穩態響應，并證明了上述非線性阻尼器可提供的最大附加模態阻尼比高于線性黏滯阻尼器。

本文研究一種非線性速度型阻尼器—新型軸向電渦流阻尼器(ball screw type axial eddy current damper，BS-ECD)對拉索多模態的減振效果。首先介紹了新型軸向電渦流阻尼器的非線性阻尼特性，并根據耗能相等的原則計算了其等效阻尼系數的解析表達式。然后基于等效線性化假定，推導了拉索附加模態阻尼比與BS-ECD設計參數之間的關系，并以使拉索多個模態附加阻尼比的最小值最大化為目標，開展了軸向電渦流阻尼器的參數優化設計和減振效果評價，最后分析了最優參數偏差和阻尼器位移幅值變化對控制效果的影響。

1 電渦流阻尼器的非線性阻尼特性

在結構振動控制領域，長期以來都認為電渦流阻尼是一種線性阻尼[22]。實際上，類似于電渦流緩速器[23]，隨著導體板與磁場之間的相對運動速度不斷增大，電渦流阻尼的速度非線性會逐漸顯著。近年來，陳政清教授團隊開發了基于滾珠絲杠的新型軸向電渦流阻尼器，如圖1所示，利用滾珠絲杠的放大作用，導體板和磁場之間的相對運動速度可以達到10 m/s的量級。通過理論分析[24]和大型阻尼器性能試驗[25-26]，表明BS-ECD的阻尼特性具有顯著的速度非線性，而且能夠用Wouterse模型進行較好地描述。

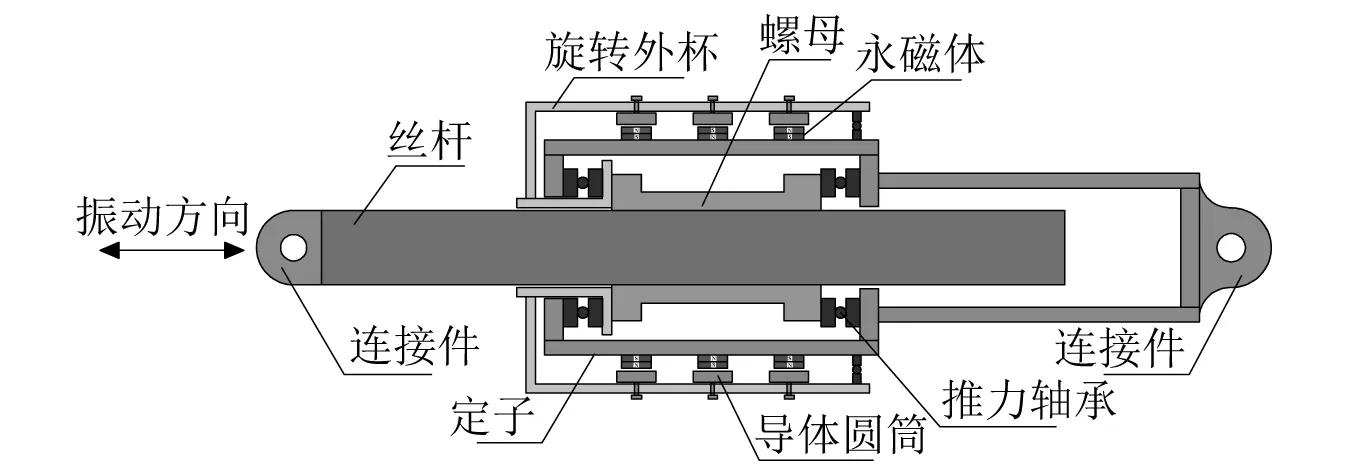
圖1 BS-ECD的構造原理示意圖Fig.1 Schematic of the BS-ECD

Wouterse[27]模型的數學表達式如式(1)所示

(1)

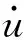
根據式(1)繪制的阻尼力速度曲線，如圖2所示。可以看到，BS-ECD的阻尼力速度非線性與傳統的液體黏滯阻尼器存在顯著差異：在臨界速度以前，電渦流阻尼力隨著軸向速度的增加而增加，但增速逐漸減小；達到臨界速度時，阻尼力達到峰值；超過臨界速度以后，電渦流阻尼力呈逐漸下降的趨勢。因此，BS-ECD的臨界速度vc越小，阻尼力的速度非線性效應越強。

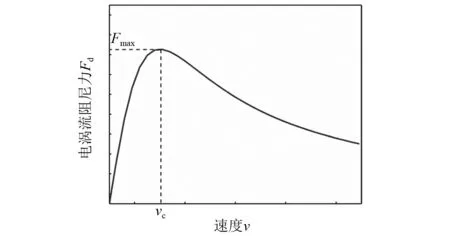
圖2 電渦流阻尼力-速度曲線Fig.2 Eddy current damping force-speed curve

根據Krenk等提出的等效線性化原則，在分析非線性阻尼器性能及參數優化時，采用阻尼力在一個周期內耗能與線性黏滯阻尼力相等來得到對應的非線性阻尼器的等效阻尼系數ceq

(2)

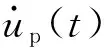
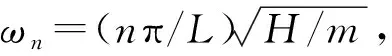
(3)

從式(3)可以看到，BS-ECD的等效阻尼系數不僅與拉索參數有關，還與阻尼器的臨界速度、峰值阻尼力，以及阻尼器安裝處拉索的位移幅值up有關。

非線性液體黏滯阻尼器是目前應用最為廣泛的一種被動耗能減振裝置，其數學模型為[28]

(4)

式中：cα為黏滯阻尼器的阻尼系數；α為速度指數; sgn(·)為符號函數。當α=1時，式(4)正好表示線性黏滯阻尼器的數學模型。非線性黏滯液體阻尼器的等效阻尼系數可表示為[29]

(5)

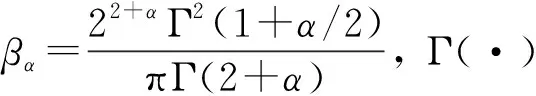
2 拉索多模態減振性能分析

2.1 拉索-BS-ECD系統的附加模態阻尼比

本文采用張緊弦模型來描述斜拉索，張緊弦-BS-ECD的物理模型如圖3所示。張緊弦模型雖然簡單，但是能反映拉索的主要受力特性，而且相關研究結論只要經過適當修正就能推廣到考慮垂度和抗彎剛度的斜拉索。

基于等效線性化原則，可以用等效阻尼系數來衡量并計算非線性阻尼器的阻尼性能和拉索-非線性阻尼器系統的等效附加模態阻尼比，其中系統的無量綱阻尼系數、模態阻尼比公式為

(6)

(7)

式中：ηn為無量綱阻尼系數；xp為阻尼器距拉索錨固端的距離；H為拉索張力；ζn為拉索第n階模態的附加阻尼比；L為拉索長度。

圖3 拉索-BS-ECD系統的張緊弦模型Fig.3 The model of taut cable with BS-ECD

觀察式(7)可以發現，當且僅當無量綱阻尼系數ηn=1時，拉索模態阻尼比達到最大值0.5xp/L。將式(3)代入式(6)，同時令ηn=1可得

(8)

由式(6)可知，對于線性黏滯阻尼器，當指定拉索安裝位置時，只存在唯一的阻尼系數使某一階的控制效果達到最優。而從式(8)可以看出，由于BS-ECD存在臨界速度vc和峰值阻尼力Fm兩個設計參數，在對阻尼器進行參數設計后，可以使拉索的第i階模態和第j階模態同時取到最優值。此時BS-ECD的臨界速度vc滿足

(9)

如果指定了拉索受控模態i和j，通過求解式(9)后可以求得相應的臨界速度vc，再代入式(8)便可以求出電渦流阻尼力峰值Fm。

接下來以Hoang等研究中的斜拉索為例，來說明軸向電渦流阻尼器的參數特點。拉索單位長度質量m=132 kg/m,索長L=540 m,張拉力H=8 270 kN，阻尼器安裝位置距拉索錨固點距離xp=10 m，阻尼器位移幅值up=2 cm。假定軸向電渦流阻尼器可以使拉索第1階模態和第4或第8或第15階模態的無量綱阻尼系數等于1，則根據式(9)和式(8)可以得到如表1所示的軸向電渦流阻尼器參數。可以看到，軸向電渦流阻尼器的臨界速度介于0.045～0.085 m/s，它可以通過調整阻尼器中的導體板厚度和滾珠絲杠的導程實現。峰值阻尼力介于16～27 kN，它可以通過調整永磁鐵的數量實現。

表1 滿足不同設計工況的軸向電渦流阻尼器參數Tab.1 The ECD’s parameters corresponding to the optimal modal damping ratio in cable’s first and highest mode simultaneously

依據等效線性化原則，對于非線性液體黏滯阻尼器而言，當ηn=1時阻尼器參數應該滿足

(10)

若假定非線性黏滯液體阻尼器也能使拉索某兩階模態的阻尼比同時達到最優值，則對應的阻尼器參數應滿足

(11)

求解式(11)可以發現，當且僅當α=0時，拉索的各階模態阻尼比可以同時達到最優，即此時非線性黏滯液體阻尼器轉變為摩擦阻尼器。

2.2 多模態減振參數優化設計方法及結果對比

長拉索的前幾階模態都有發生大幅振動的可能，所以對于拉索的多模態減振，設計目標應使拉索前幾階模態的附加阻尼比都盡可能大。根據該設計目標，當確定了設計關注的拉索前n階模態后，軸向電渦流阻尼器的參數采用如下方式進行優化：確定一組電渦流參數(Fm,vc)，使拉索前n階模態中模態阻尼比的最小值達到最大，即求解下列最優化問題

在部署方式上，支持分布式部署和負載均衡配置。各子站擁有獨立的域名，并支持獨立的子站維護管理體系，同時主站與各子站、子站間的信息可以互相共享呈送，實現站點間的數據調度與交換，即采用“Web服務器+數據庫服務器+數據存儲”架構。網站群的主站與各子站Web應用和數據庫可部署在同一或不同服務器上。

max{min[ζ1(Fmax,vc),ζ2(Fmax,vc),…,
ζn(Fmax,vc)]}

(12)

非線性黏滯阻尼器的參數采用同樣的目標進行優化。

以2.1節所述的拉索參數和阻尼器安裝位置為例，基于上述優化策略，分別以拉索前4階和前8階模態為控制目標，求解了軸向電渦流阻尼器的最優臨界速度和最優峰值阻尼力，結果如表2所示。可以看到，由上述優化策略得到的電渦流最優臨界速度與表1中通過式(9)所求得的結果一致，但兩種情況下所得到的峰值阻尼力不同。這表明在上述多模態優化策略所得到的電渦流最優臨界速度下，通過調整電渦流阻尼器的峰值阻尼力可以使拉索第1階和第n階模態的無量綱附加阻尼比同時達到最大值0.5。

表2 電渦流阻尼器參數優化結果Tab.2 Optimization results of critical speed parameters of eddy current damper

圖4(a)和圖4(b)分別給出了拉索受控模態為1～4階和1～8階時,拉索無量綱附加模態阻尼比ζn/(xp/L)隨BS-ECD峰值阻尼力的變化規律，其中阻尼器的臨界速度取表2所示的最優值。可以看出，第1階和第n階模態阻尼比曲線正好重合，而從第2～第n階模態，與最大附加模態阻尼比0.5xp/L對應的阻尼器峰值阻尼力隨著模態階次的增加而緩慢增加，從而使BS-ECD可以達到更好的多模態減振效果。以圖4(b)為例，與第2階模態最大附加阻尼比對應的阻尼力峰值為12 kN，而與第8階模態對應的峰值阻尼力為22 kN。

圖4 最優臨界速度下拉索無量綱模態阻尼比隨峰值阻尼力的變化曲線Fig.4 Variations of cable’s modal damping ratio in different orders under the optimal critical velocity

從圖4可以進一步得到，當臨界速度和峰值阻尼力都取最優值時，拉索各階模態的無量綱附加阻尼比結果如圖5所示。從圖5(a)可以看到，當拉索受控模態為1～4階時，各階模態無量綱附加阻尼比分別為0.496，0.494，0.498和0.498，都非常接近最大值0.5；從圖5(b)可以看到，當拉索受控模態為1～8階時，各階模態無量綱附加阻尼比都大于0.48，說明BS-ECD對拉索的多模態振動有較好的控制效果。

圖5還對比了BS-ECD與非線性液體黏滯阻尼器的優化結果。可以看到，速度指數α越小，非線性液體黏滯阻尼器的多模態減振效果就越好，其中當α=0.3時，拉索各階模態的附加阻尼比與軸向電渦流阻尼器基本相當。當非線性液體黏滯阻尼器退化為線性黏滯液體阻尼器時，多模態控制效果較差。

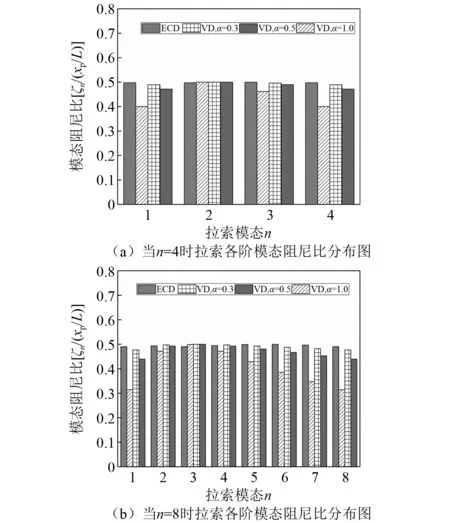
圖5 電渦流阻尼器與黏滯阻尼器對拉索多模態減振性能比較Fig.5 Comparison of eddy current damper and viscous damper on cable’s multi-mode vibration control performance

3 多模態減振效果地參數敏感性分析

3.1 阻尼器最優參數敏感性分析

在實際工程中，BS-ECD的實際參數可能偏離最優設計值，因此有必要分析多模態減振效果對阻尼器最優參數的敏感性。分別考慮阻尼力峰值Fm和臨界速度vc從最優值偏離±20%，得到受控模態分別為第1～4階和第1～8階時，拉索附加模態阻尼比的變化情況，如圖6和圖7所示。

從圖6(a)和圖6(b)可以看到，當峰值阻尼力或臨界速度從最優值偏離時，BS-ECD能為拉索前4階模態提供的附加阻尼比最小值的最大值都會有一定程度的降低，但降幅非常小。例如，當峰值阻尼力最優值偏離-20%時，前4階模態的無量綱模態附加阻尼比中的最小值從0.497降低到0.475，相對降幅為4.6%；當臨界速度從最優值偏離-20%時，前4階無量綱模態附加阻尼比中的最小值降低到0.488，相對降幅為1.9%。

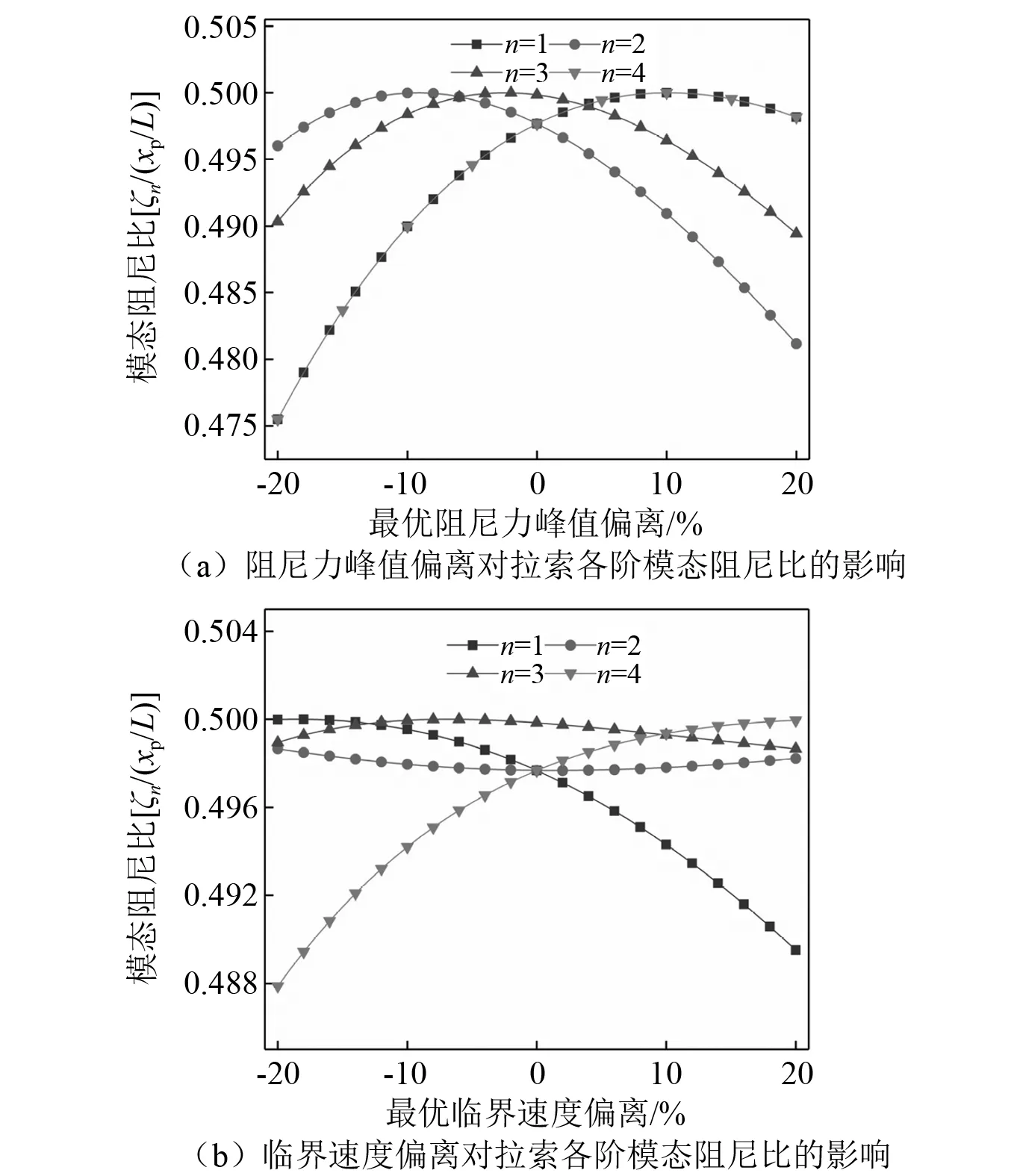
圖6 最優電渦流阻尼參數敏感性分析(n=4)Fig.6 Sensitivity analysis of optimal ECD parameters (n=4)

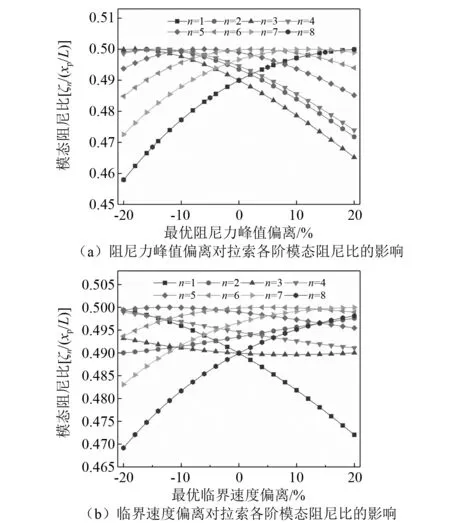
圖7 最優電渦流阻尼參數敏感性分析 (n=8)Fig.7 Sensitivity analysis of optimal ECD parameters (n=8)

綜上所述，BS-ECD對拉索前8階模態的減振效果和阻尼器的最優參數偏離敏感度都較低，因此能夠較好地適應實際工程中的設計和制作偏差。

3.2 阻尼器位移幅值敏感性分析

由式(3)可知，拉索-BS-ECD系統的模態阻尼比除了與拉索和阻尼器物理參數有關以外，還與阻尼器的位移幅值相關。實際工程采用的拉索可在一定行程范圍內工作，因此有必要分析附加模態阻尼比對阻尼器位移幅值的敏感性。表2給出的參數優化結果是針對阻尼器安裝處拉索的位移幅值等于0.02 m的情況。圖8在此基礎上分析了當阻尼器位移幅值變化時，拉索前4階或前8階模態附加阻尼比的變化情況。

從圖8(a)和圖8(b)可以看到，當BS-ECD的工作行程偏離其設計位移幅值時，各階模態的附加阻尼比都會逐漸降低，而且模態階次越高，受到的影響就越大。例如，在圖8(a)中，當阻尼器位移幅值在0～0.02 m內變化時，拉索第1階模態的阻尼比變化幅度僅為3.3%，但第4階模態的無量綱模態阻尼比從設計值0.498降低到了0.18，降幅達到了60%左右。對比圖8(b)和圖8(a)可以發現，隨著受控模態階次的增多，高階模態的附加阻尼比受阻尼器位移幅值的影響也越明顯。

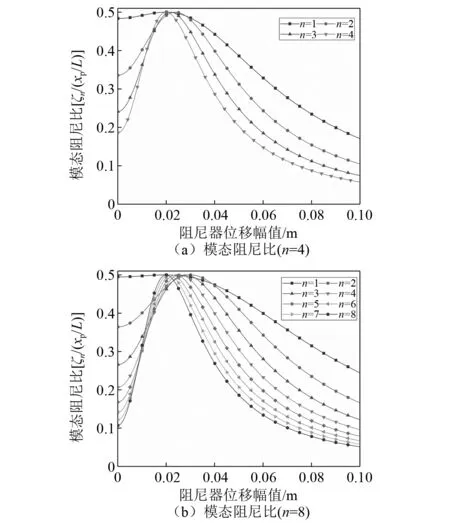
圖8 拉索各階模態阻尼比隨阻尼器位移變化情況比較Fig.8 Comparison of the damping ratio of each mode of the cable with the displacement of the damper

盡管由BS-ECD提供的拉索附加模態阻尼比對阻尼器位移幅值比較敏感，但振幅敏感性可能并不會降低BS-ECD這類非線性阻尼器對風雨振、渦振等拉索流固耦合振動的減振控制效果。從理論上看，在風荷載作用下，拉索的位移響應是逐漸增加的，當阻尼器位移響應未達到設計值時，它提供的附加阻尼比也較小，此時拉索和阻尼器的位移響應都繼續增加。當阻尼器的位移響應增加到接近設計值時，它提供的附加模態阻尼比也達到設計目標，此時阻尼器耗能和風荷載輸入的能量達到平衡，拉索響應不再增加。因此，如從時域上看，振幅依賴性可能不會對BS-ECD的減振效果造成影響，但仍應再仔細研究。

針對非線性阻尼器拉索減振性能的振幅依賴性，Hoang等提出將具有振幅依賴的拉索附加模態阻尼比在阻尼器的工作行程ΔDc內平均，得到具有行程平均意義的附加模態阻尼比。對于電渦流阻尼器而言，行程平均意義的模態阻尼比可表示為

(13)

根據式(13)，圖9(a)和圖9(b)給出了當阻尼器工作行程設計值為0.02 m拉索受控模態分別為前4階和前8階時，拉索前4階和前8階的平均附加模態阻尼比隨峰值阻尼力的變化情況。可以發現，考慮行程平均后，各階模態附加阻尼比的峰值均有不同程度的下降，而且模態階次越高，降低越嚴重。然而值得注意的是：即便在行程平均后拉索各階模態阻尼比的最大值會略有下降，但對于拉索多模態的減振效果來說電渦流阻尼器還是要明顯優于線性黏滯阻尼器。例如，對于拉索前8階模態的減振控制，從圖9(b)可以看到當BS-ECD的臨界速度按2.2節的優化結果取0.063 m/s，阻尼力峰值取9.75 kN，則BS-ECD能夠為拉索第1～8階模態的無量綱附加模態阻尼比在0.408～0.494；另一方面，從圖5(b)可以看到，當線性黏滯阻尼器按多模態減振控制優化時，它可為拉索前8階模態提供的無量綱附加阻尼比在0.314～0.500，從控制效果的下限來看，明顯低于BS-ECD。

綜上所述，在進行實橋拉索減振設計時，可以按照式(13)計算安裝電渦流阻尼器以后拉索各階模態的附加阻尼比，其中ΔDc取為電渦流阻尼器的設計行程，這樣可以偏保守地估計電渦流阻尼器的減振性能。

4 結 論

本文基于等效線性化理論分析了軸向電渦流阻尼器的速度非線性對拉索附加模態阻尼比的影響，并針對拉索多模態控制，計算了軸向電渦流阻尼器的最優臨界速度、峰值阻尼力和附加模態阻尼比，評價了其減振性能，最后分析了阻尼器減振效果對最優參數和位移峰值的變化的敏感性。主要結論如下：

(1) 存在一組軸向電渦流阻尼器的臨界速度和峰值阻尼力，可以使拉索任意兩階模態的附加阻尼比同時達到最大值。

(2) 當指定阻尼器的工作行程時，通過參數優化可以使軸向電渦流阻尼器的多模態減振效果優于線性黏滯阻尼器和非線性液體黏滯阻尼器，且減振效果對最優參數變化不敏感。

(3) 與其他非線性阻尼器一樣，軸向電渦流阻尼器提供的附加模態阻尼比也具有明顯的振幅依賴性，當阻尼器的工作行程偏離設計值時，其減振效果會有較明顯的降低，后續應仔細研究。