流冰撞擊作用下川藏鐵路橋梁振動抑制及行車安全研究

李鵬浩， 翟婉明， 和振興， 石廣田

(1. 蘭州交通大學 機電工程學院，蘭州 730070； 2. 西南交通大學 牽引動力國家重點實驗室，成都 610031)

川藏鐵路是我國西南地區在建的重要鐵路干線，連接成都和拉薩，新建正線長約1 549 km，設計時速160～200 km/h。川藏鐵路沿線地區環境氣候多變、地質復雜、災害頻發，具有高寒缺氧、高烈度地震、高海拔和大高差等“三高一大”的特征[1-3]。川藏鐵路沿線的部分橋梁面臨著來自冰湖潰決和冰融季節時河流和湖泊中流冰的撞擊。與車輛、船舶、泥石流和落巖等撞擊不同[4-7]，流冰撞擊橋墩時產生的撞擊力相對較小，但具有持續時間較長，撞擊頻率高等特點，撞擊危害不能忽視。橋梁受到撞擊時，會產生梁體相對支座的偏移，嚴重時甚至導致支座損壞，給橋梁結構帶來安全隱患[8-9]；流冰撞擊還會影響橋上軌道結構的平順性，由此引起的動態輪軌力會隨車速的增加而顯著增大，可能對乘客的乘坐舒適性和列車的運行安全性造成影響[10]。

車橋振動是鐵路動力學的經典課題，經過幾十年的發展，形成了兩種典型的模型：車-橋耦合振動和列車-軌道-橋梁動力相互作用[11-13]。近年來，許多學者基于列車-軌道-橋梁動力相互作用理論，評估了各類橋梁的動力學性能以及橋上列車的走行性和安全性；也有一些學者提出新的混合求解算法，旨在提高計算精度和效率[14-15]。除了研究車-線-橋系統的自激振動外，外部環境激勵對車-線-橋系統的影響也引起廣泛關注，如強風、地震和撞擊等[16-17]。Xia等[18-19]研究了流冰撞擊對車-橋系統的影響，評估橋上列車運行安全性，并分析了行車速度和撞擊強度的閾值關系。當流冰撞擊強度和列車速度到一定限值時，橋上列車存在脫軌的危險。

動力吸振器(dynamic vibration absorbers，DVA)是一種常用的減振裝置，它由質量塊、彈簧和阻尼器組成，具有簡單、可靠、廉價的特點，近年來被廣泛應用于土木結構振動控制領域。Frahm[20]于1911年提出了在單自由度結構上附加無阻尼DVA，這是DVA的首次應用。Ormondroyd等[21]在Frahm發明的DVA基礎上加入了阻尼器，這樣不僅增強了減振效果，還拓寬了減振頻帶，并提出了著名的定點理論。Hahnkamm[22]依據定點理論推導了DVA的最優頻率比和最優阻尼比。Zhu等[23]研究了動力吸振器對浮置板軌道的低頻振動控制，振動控制效果顯著。楊吉忠等[24-25]基于動力吸振原理研究了高墩橋梁的抗震特性并分析了列車過橋的安全性，得出動力吸振型橋梁在地震荷載作用下減振效果突出的結論。

目前DVA減振技術在橋梁工程中多用在橋梁抗震領域，而關于撞擊荷載作用下DVA減振控制未見研究。為了研究DVA對流冰撞擊作用下橋梁的振動抑制和對列車行車安全性的影響，本文組織結構如下：第1章概述列車-軌道-橋梁-冰擊模型理論；第2章介紹DVA設計方法；第3章研究DVA對冰擊荷載作用下橋梁結構的振動抑制；第4章分析DVA對冰擊荷載作用下列車行車安全性的影響。

1 流冰撞擊作用下列車-軌道-橋梁動力相互作用模型

基于列車-軌道-橋梁動力相互作用仿真框架[26-27]，流冰撞擊作用下的列車-軌道-橋梁系統由列車和軌道-橋梁兩個子系統組成。子系統之間通過輪軌相互作用和橋軌相互作用耦合。模型中有兩個激勵源：軌道幾何不平順引起的自激激勵和作為外荷載施加到大系統中的流冰撞擊力。動力學模型如圖1所示。

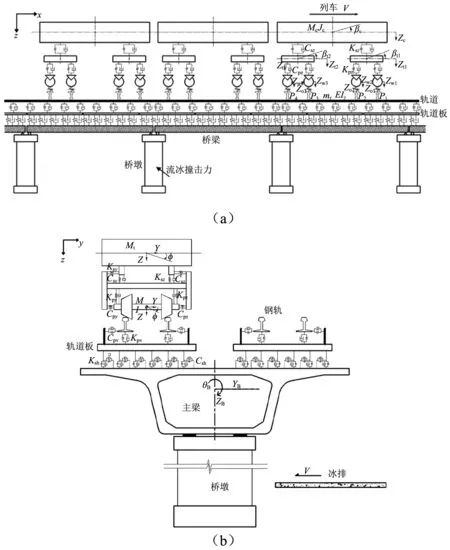
圖1 列車-軌道-橋梁-冰擊動力學模型Fig.1 Dynamics model of train-track-bridge system under floating ice impact loads

1.1 車輛模型

車輛模型由1個車體、2個構架和4個輪對組成。車體、構架和輪對各有5個自由度，車輛模型共35個自由度。車輛動力學方程為

(1)

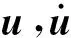
1.2 軌道-橋梁模型

模型中左右兩股鋼軌被視為連續的Timoshenko梁，考慮了鋼軌的垂向、橫向和扭轉振動，計算中為模擬軌道板和鋼軌之間的力學關系，采用離散黏彈性單元模擬了扣件的剛度和阻尼特性。橋梁采用有限元方法建模，主梁和橋墩均采用實體單元。建模中假定：①橋梁模型與實際工程中結構吻合，在不影響主要力學性能的前提下進行一定的簡化；②橋梁在撞擊過程中只發生小變形，結構始終處于線彈性范圍。軌道-橋梁動力學方程表示為

(2)

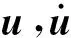
橋梁結構阻尼采用Rayleigh阻尼。假定結構的阻尼矩陣是質量矩陣和剛度矩陣的組合，即

C=αMb+βKb

(3)

(4)

式中：ωi和ωj分別為橋梁結構的第i和第j階參考頻率[28]；ζb為橋梁的阻尼比。

1.3 輪軌接觸關系

本文采用新型輪軌空間耦合模型[29]來模擬輪軌非線性接觸幾何關系，輪軌法向力用赫茲非線性理論計算，輪軌切向力采用kalker線性蠕滑理論計算[30]。

1.4 流冰撞擊荷載

流冰撞擊荷載通常由兩種方法獲得：一是現場試驗采集撞擊力；二是通過有限元法仿真獲得。本文通過建立流冰-橋墩撞擊模型計算了流冰撞擊荷載。橋墩采用線彈性材料模擬，參考河冰單軸壓縮試驗數據[31]，冰排采用與應變率相關的塑性材料模擬，以最大拉應力作為冰排破壞失效準則。

將計算得到的流冰撞擊力作為外部荷載施加到列車-軌道-橋梁系統中，此時橋梁子系統的動力學方程為

(5)

式中，Rc為流冰撞擊力。

2 DVA設計方法

在進行DVA減振系統設計時，需確定DVA的三個主要參數：質量比、剛度和阻尼。圖2所示為隨機激勵作用下單自由度結構-DVA減振系統力學模型。

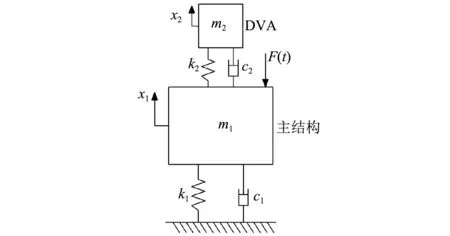
圖2 隨機激勵作用下主結構-DVA減振模型Fig.2 DVA-primary structure subject to a random excitation

根據達朗貝爾原理，DVA作用下系統的運動方程為

(6)

式中：m1，k1，c1分別為主結構的質量、剛度和阻尼系數；m2，k2，c2分別為DVA的質量、剛度和阻尼系數；x1為主結構位移；x2為DVA位移；F(t)為外部隨機荷載。

基于定點理論，Ormondroyd等推導出附加在單自由度帶阻尼結構上的DVA的最佳剛度和阻尼解析式

(7)

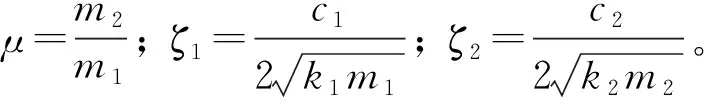
由于橋梁是一個連續體結構，計算單自由度系統DVA最優參數的方法不能直接用于橋梁結構的DVA設計。文獻[32]將經典的Den Hartog方法推廣到多自由度結構，并推導出了最佳設計參數和最佳安裝位置。本文參考文獻[33]，將橋梁結構離散成一個多自由度系統，再基于模態分析、等效質量識別法，建立了由多個單自由度系統組成的非耦合系統。因此采用單自由度系統DVA的設計方法，可以設計橋梁結構上施加DVA的最優參數。

(8)

式中：mij為橋梁結構第i階模態j點處的等價質量；T為系統動能；ωi為第i階固有頻率； {X1…Xj…XN}為系統特征向量；{M1…Mj…MN}為離散的單自由度質量；kij為橋梁結構第i階模態j點處的等價剛度。

由式(7)、式(8)可知，當求得DVA質量比μ、橋梁結構等價剛度kij和等價阻尼cij后，即可求出DVA的最佳剛度和阻尼。但橋梁結構的等價阻尼cij很難通過計算求得，因此不能直接采用式(7)得到DVA的最佳剛度。式(9)所示為無阻尼單自由度結構附加DVA的最佳剛度計算公式

(9)

參考文獻[34]可知，可先采用式(9)計算出一個初始剛度值，再根據最優同調條件，適當調小初始剛度來獲得DVA的最佳剛度值。

3 橋梁撞擊振動抑制

3.1 結構模型及動力特性分析

以川藏鐵路典型的簡支箱梁為例，采用ANSYS建立橋梁有限元模型，截面尺寸和橋梁布置如圖3所示。建模中主梁和橋墩均采用solid65單元，網格尺寸0.4 m×0.4 m×0.4 m，橋面二期恒載作為附加質量分布到橋面上，采用mass21單元模擬，取值120 kN/m。為準確模擬橋梁支座和基礎的作用，主梁和支座、橋墩和基礎的連接采用彈簧單元模擬，該力元可以有效模擬支座和基礎的剛度和阻尼特性。

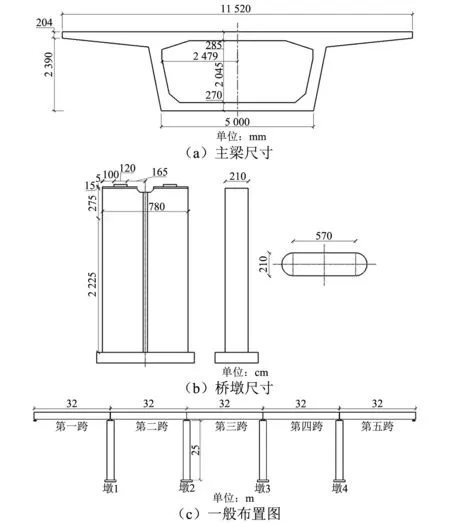
圖3 典型鐵路簡支箱梁結構 Fig.3 The typical railway simply-supported box girder structure

采用ANSYS對上述有限元模型進行模態分析，因流冰撞擊主要影響橋梁結構的橫向振動，因此本文只分析橋梁的橫向振動模態，圖4所示為橋梁前兩階橫向振型。

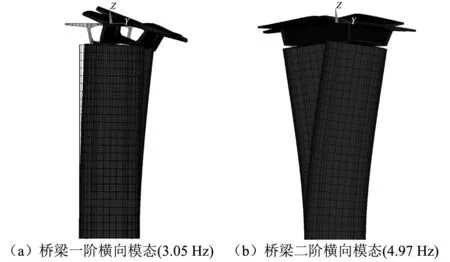
圖4 橋梁前兩階橫向振動模態Fig.4 The first two lateral mode shapes of the bridge

3.2 流冰撞擊荷載計算

本文采用LS-DYNA建立流冰-橋墩撞擊有限元模型，冰排尺寸為40 m×20 m×0.4 m。建模中橋墩和冰排均采用solid164單元模擬，橋墩單元尺寸為0.4 m×0.4 m×0.4 m，冰排中間部分單元大小為0.15 m×0.15 m×0.2 m，冰排兩端單元尺寸大小為0.15 m×0.4 m×0.2 m，冰排撞擊位置為距墩底5 m處。模型計算過程中，接觸類型采用面與面自動接觸，接觸算法采用對稱罰函數算法，詳細建模步驟參考文獻[35]。圖5所示為冰排抗壓強度為2 MP時冰擊力曲線。

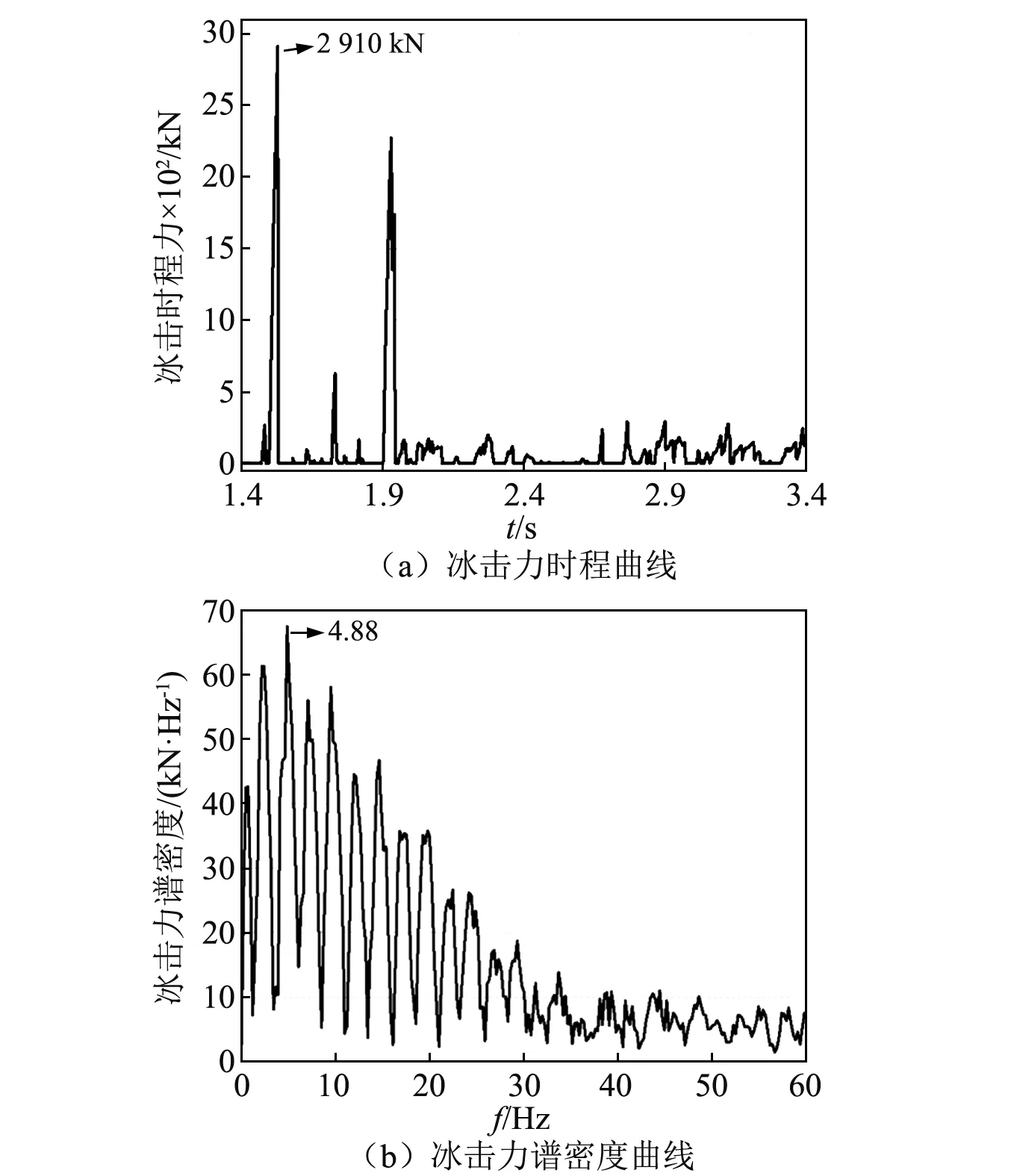
圖5 冰擊時程力Fig.5 The ice impact loads

3.3 DVA最優參數設計和最佳安裝位置

考慮到流冰撞擊的最不利工況，將計算得到的冰擊時程力以外荷載的形式加在所有的橋墩上，撞擊位置為距墩頂10 m處，計算冰擊荷載作用下橋梁結構的動力學響應。圖6所示為冰擊荷載作用下橋梁第三跨跨中和2號墩頂橫向位移時程曲線和功率譜密度曲線。

由圖6可知，冰擊荷載作用下，橋梁跨中和墩頂橫向位移急劇增大，冰擊荷載的主頻和橋梁結構二階橫向振動模態接近，可能激起此階頻段附近更大的振動，因此本文以橋梁二階模態為控制對象，設計DVA的最佳參數。由圖4可知，橋梁二階橫向振動墩頂位移最大，因此DVA安裝在墩頂處，每個墩頂安裝一個DVA。表1為質量比μ=0.1時，DVA的最佳剛度和阻尼。

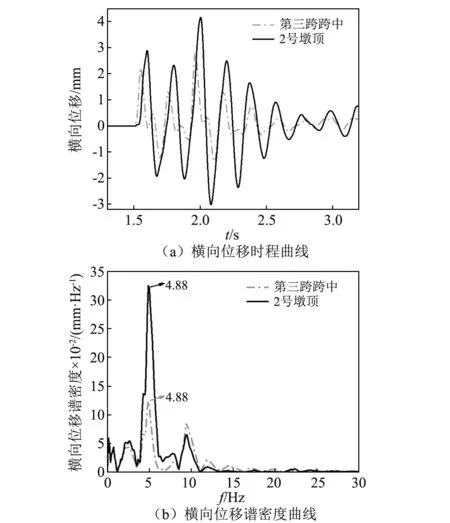
圖6 橋梁結構橫向位移Fig.6 Lateral displacement of the bridge

表1 DVA最優參數Tab.1 Optimal parameters of DVA

3.4 DVA減振特性分析

基于上述DVA的最優參數設計，分析墩頂安裝DVA對冰擊荷載作用下橋梁跨中和墩頂橫向位移的影響。圖7所示為兩種工況下(有DVA和無DVA)橋梁第三跨跨中和2號墩頂橫向位移在時域和頻域的響應。

當墩頂附加DVA 后，橋梁受到撞擊產生的能量通過彈簧-阻尼力元傳遞給DVA，這一過程使能量得到耗散，橋梁結構橫向位移顯著減小，其中跨中和墩頂橫向位移分別下降約48.6%和35.3%。由圖7(b)可知，當橋梁不附加DVA時，由冰擊荷載引起的橋梁跨中和墩頂橫向位移在橋梁固有頻率4.97 Hz附近出現較大的峰值；而附加DVA后，橋梁在此頻段的橫向位移顯著降低，表明DVA能有效抑制冰擊荷載作用下橋梁結構的橫向振動。

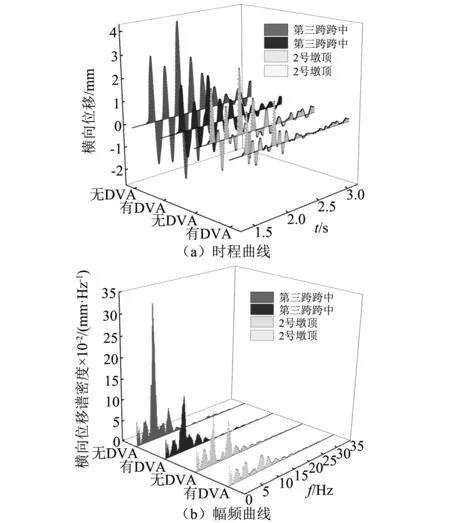
圖7 橋梁跨中和墩頂橫向位移曲線Fig.7 The lateral displacement of the bridge mid-span and the top of the pier

4 冰撞作用下墩頂附加DVA對列車走行性的影響

采用前述的列車-軌道-橋梁-冰擊動力學模型，列車采用8節車編組，軌道不平順采用德國高干擾譜，波長1～45 m，考慮到流冰撞擊橋墩的最不利情況，當列車行駛到橋梁第三跨時，流冰同時撞擊所有橋墩，撞擊位置為距墩頂10 m處。

4.1 行車速度對冰擊作用下列車動力學響應的影響

為了研究DVA對不同行車速度下車輛動力學響應的影響，本文控制DVA質量比μ=0.1，行車速度為160 km/h，200 km/h，計算分析不同時速下車輛的動力學響應。圖8所示為不同時速下車輛動力學響應峰值，圖9為車體橫向振動加速度譜密度曲線，圖10為DVA對車輛振動的減振率。

圖8 不同時速下車輛動力學響應峰值Fig.8 Peak of train dynamic responses at different speeds

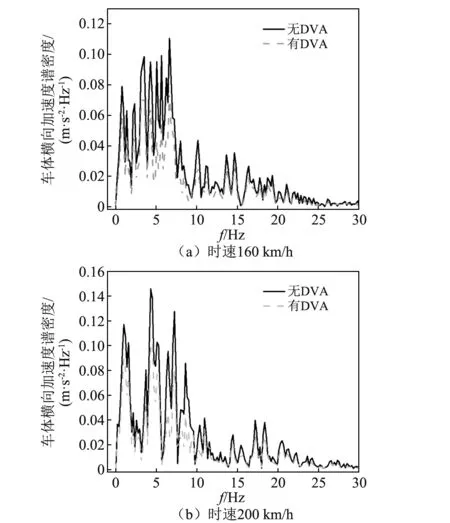
圖9 不同時速下車體橫向加速度譜密度曲線Fig.9 Power spectral density of lateral acceleration of car body at different speeds

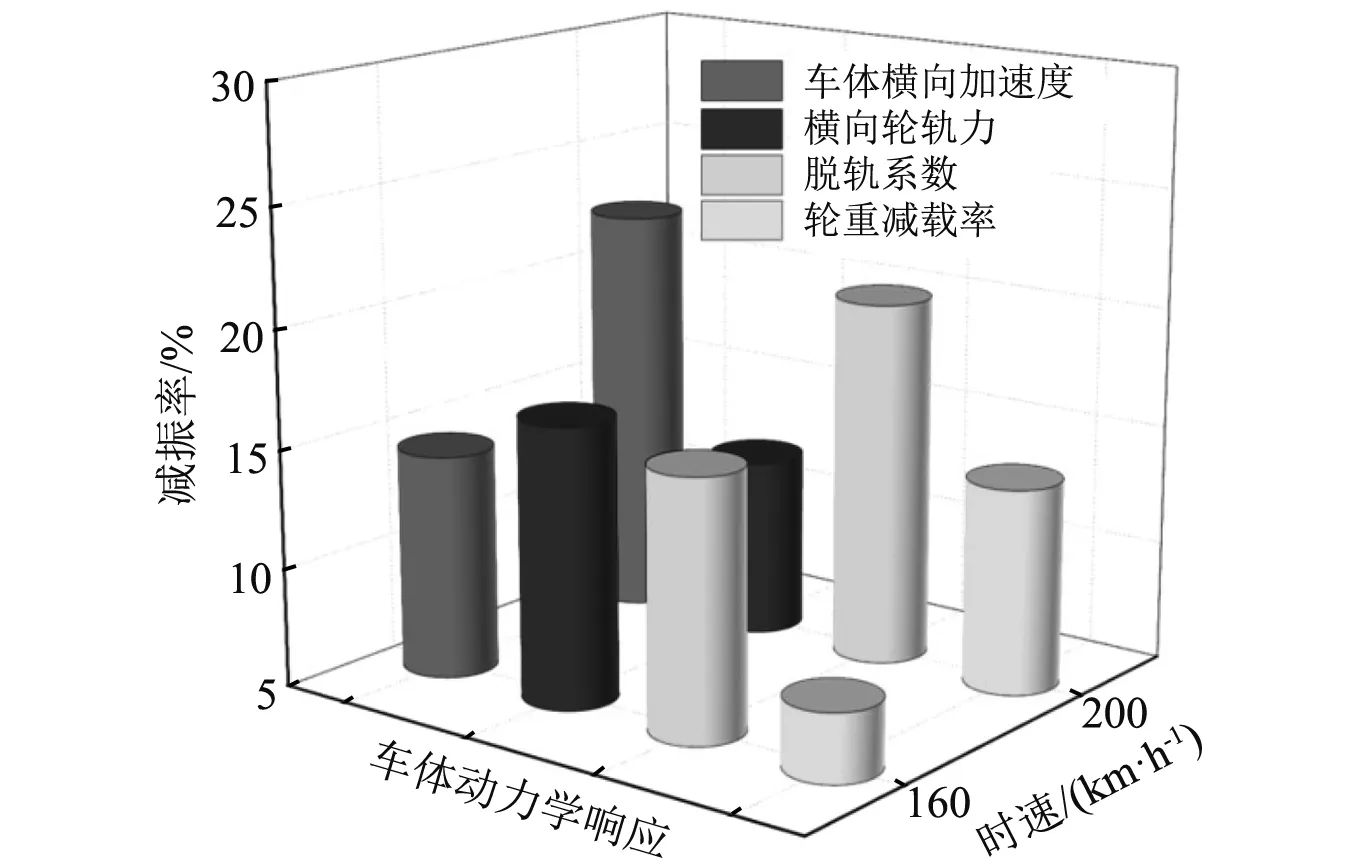
圖10 車輛動力學響應振動抑制效果Fig.10 Vibration suppression effect of train dynamic response

由圖(8)可知，在冰擊荷載作用下，隨著行車速度的增加，車體橫向振動加速度、輪軌橫向力、脫軌系數和輪重減載率均增大；當橋上附加DVA后，車輛動力學響應均不同程度的減小。分析圖9可知，DVA顯著降低了車體橫向振動加速度在低階頻段的振動；由圖10不難發現，行車速度為200 km/h時，DVA對流冰撞擊作用下的車輛動力學響應的減振效果總是大于行車速度為160 km/h時的結果，表明DVA對列車振動有較好的抑制作用。

4.2 DVA質量比對列車動力學指標的影響

本節研究了DVA質量比對流冰撞擊作用下列車動力學響應的影響。選取列車時速為160 km/h，DVA的質量比分別取0.05，0.10，0.15。圖11為不同質量比DVA對車輛動力響應的影響和車體振動加速度譜密度曲線。

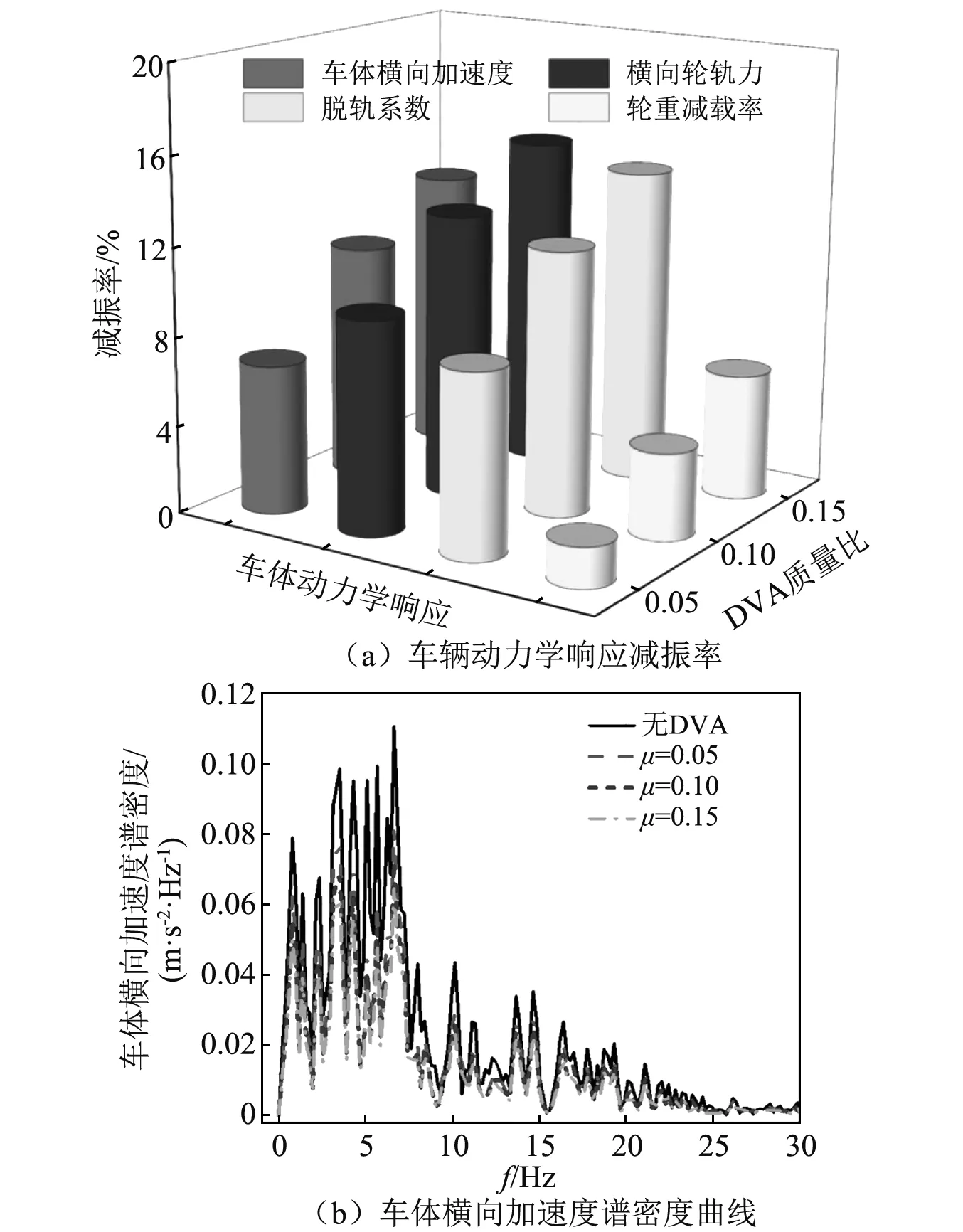
圖11 不同質量比DVA時車輛動力學響應抑制效果Fig.11 Vibration suppression effect of train dynamic response under different mass ratio of DVA

由圖可知，隨著DVA質量比的增加，車體橫向振動加速度、橫向輪軌力、脫軌系數和輪重減載率的減振效果均增大；當橋墩頂附加DVA后，車體橫向振動加速度在低階頻段內的振動得到了明顯的抑制，但隨著DVA質量比的增加，振動抑制增加的效果隨之減小，表明在滿足工程需求的前提下，不必刻意增大DVA質量比。

5 結 論

本文基于列車-軌道-橋梁動力相互作用理論和DVA設計方法，建立了冰擊荷載作用下列車-軌道-橋梁-DVA動力學模型，探討了DVA的最優參數和最佳安裝位置，研究了冰擊荷載作用下DVA對橋梁結構的減振特性和車輛動力學響應的抑振效果，得出以下結論：

(1) 冰擊荷載作用下橋梁跨中和墩頂橫向位移急劇增大，橋梁跨中和墩頂橫向位移主頻與冰擊荷載主頻一致，且接近橋梁二階橫向振動頻率，這可能會激起橋梁結構在此階頻段更大的振動。

(2) 橋上安裝DVA后，有效抑制了流冰撞擊作用下橋梁結構的橫向振動，在本文算例條件下跨中和墩頂橫向位移分別下降約48.6%和35.3%，且在DVA作用下顯著降低了橋梁結構橫向位移主頻峰值。

(3) 在DVA作用下，列車過橋時的車體橫向振動加速度、橫向輪軌力、脫軌系數和輪重減載率等動力學指標均明顯減小；隨著車速的增加，除橫向輪軌力外，DVA對列車其他動力學指標的減振效果均增大；保持行車速度不變，列車動力學指標的減振率均隨著DVA質量比的增加而增大。