基于幾何多重網格預條件技術的三維大地電磁高效正演模擬

王永斐， 柳建新,3， 郭榮文,3*， 劉嶸， 李健，陳杭， 楊剛強

1 中南大學地球科學與信息物理學院， 長沙 410083 2 有色資源與地質災害探查湖南省重點實驗室， 長沙 410083 3 中南大學有色金屬成礦預測與地質環境監測教育部重點實驗室， 長沙 410083

0 引言

大地電磁(MT)法作為電磁(EM)法(盧杰和李予國，2019；楊海燕等，2019；底青云等，2020；何展翔等，2020)的一種，廣泛應用于解決各種工程和科學問題，例如油氣勘探(夏訓銀等，2012；He et al.，2015)、地熱調查(Newman et al.，2008)、礦產勘探(高才坤等，2009)和深部電性結構的研究(金勝等，2012；劉營等，2013；王剛等，2017；崔騰發等，2020)等.它的成功應用離不開MT數據的解釋，其中重要一環是MT數據的反演解釋.數據的反演(Avdeev, 2005; Yang et al., 2014, 2016; 周思杰和黃清華，2018；彭榮華等，2019；阮帥等，2020)是建立在正演問題的求解基礎上，正演求解的效率很大程度上決定了反演的效率.然而MT勘探范圍較大，比如我國的SinoProbe項目等(Dong et al., 2013；楊文采等，2020)，精細反演解釋需要大量模型單元，在現有正演算法的計算效率下，要開展全區域數據的精細反演解釋，即便是采用目前最先進的高性能計算機也具有挑戰性(Zhdanov et al., 2011).因此快速MT的正演研究一直是MT勘探的一個研究熱點(李焱等，2012；殷長春等，2017；秦策等，2020).

由于地球深部結構比較復雜，MT正演結果往往無法解析獲得，需要通過數值近似.常用的數值模擬方法有有限元法(FEM)(Ren et al., 2013, 2014；蔡紅柱等，2015；湯文武等，2018；顧觀文和李桐林，2020；惠哲劍等，2020；齊彥福等，2020)、積分方程法(IEM)(陳桂波等，2009；任政勇等，2017；Liu et al., 2018；Wang et al., 2019)和有限差分法(FDM)(Egbert and Kelbert, 2012；李焱等，2012；董浩等，2014；Dong and Egbert, 2019；孫懷鳳等，2021).基于電磁場雙旋度方程的交錯網格FDM，由于其實現簡單和靈活，已廣泛應用于3D MT數據的反演(董浩等，2014；Kelbert et al., 2014).

MT正演的數值求解往往涉及的計算區域比較大，其正演方程的離散得到的是大型稀疏矩陣，通常很難用直接求解方法進行求解.一般采用的是基于Krylov子空間的迭代算法進行求解，如穩定雙共軛梯度法(BiCGstab)(Van der Vorst, 1992)、擬最小殘差法(QMR)(Freund, 1993)等.由于離散的Maxwell方程存在豐富的零空間，常用的迭代方法很難收斂，且當頻率趨向于零時離散方程無法保證電流散度處處為零.為了提高正演效率，通常需要采用預條件技術，如超松弛預條件(SSOR)(Chen et al., 2002)、分塊不完全LU分解預條件(block ILU)(柳建新等，2009)和高斯預條件(GS)(Adams et al., 2003)技術，以及散度校正(Dong and Egbert，2019)來改善迭代算法的收斂性.但是隨著網格數量的增加和頻率的降低，這些方法的收斂性同樣會變差(Koldan et al., 2014).

多重網格法(MG)(Oosterlee, 1997；魯晶津等，2009；Horesh and Haber, 2011；柳建新等，2011; Pan et al., 2017)將細網格上的大型方程求解問題轉換到較粗網格上的更小的方程組求解問題，有效的消除高頻誤差和低頻誤差，從而達到快速求解方程的目的.且其計算量隨著網格數的增加呈線性增加，因此廣泛應用于求解大型橢圓型微分方程問題.它包含代數多重網格法(AMG)(魯晶津，2010; Koldan et al., 2014；Chen et al., 2017)和幾何多重網格法(GMG)(J?nsth?vel, 2006；Mulder, 2006, 2008; Li et al., 2016a, b; Guo et al., 2022).由于GMG構造各算子簡單、高效，該方法常用于構建高效的大型方程組求解器或預條件技術(Aruliah and Ascher, 2002；Koldan et al., 2014；Hassan et al., 2019).但是隨著方程組各向異性的增強(由模型網格拉伸的加大等引起)，GMG的收斂效率會有所降低.Mulder (2006)表明將GMG與基于Krylov子空間的迭代求解方法相結合可以改善其收斂性.

但是如果采用傳統的平滑算法如GS等，當頻率比較低時，即便采用散度校正，GMG也無法有效的把高頻誤差平滑掉(Li et al., 2020).這時可以將場的方程轉化為矢量勢和標量勢方程(Bochev et al., 2008)或采用分塊GS平滑算法，即通過一次計算一個局部小型方程組(比如一個點所連接的六個分量)來改善GMG的收斂性(J?nsth?vel, 2006).但是這種逐點迭代涉及大量的迭代過程，通常計算比較耗時.針對該問題，Li等(2020)提出四色分塊GS平滑算法，避免了逐點迭代，顯著提高了分塊GS平滑算法效率.如果該方法能用來作為GMG的平滑算法，將會大大提高GMG的計算效率.

本文結合四色分塊GS為平滑算法GMG和BiCGstab，提出一種高效的MT正演方法.該方法將四色分塊GS為平滑算法GMG作為BiCGstab的預條件技術，以最大程度地利用這兩種方法的優點.為了驗證算法的正確性和高效性，本文基于三個合成模型對比了本文提出的正演方法和基于BiCGstab的傳統預條件技術(GS、block ILU和SSOR)的迭代次數和收斂時間.

1 交錯網格有限差分法

由于MT所采用的頻率比較低，因此在大地中可以忽略位移電流的作用.假設時諧因子為eiω t并且使用國際標準單位.在頻率域中可以將電磁場的麥克斯韋方程組進行簡化，得到關于電場的二階偏微分方程：

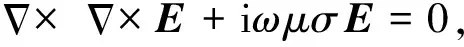
(1)

式中E表示電場矢量，σ和μ分別表示電導率和磁導率，ω為角頻率.結合邊界條件，就可以對(1)式進行數值和/或解析求解，本文采用的邊界條件為狄利克雷第一類邊界條件.

圖1 交錯有限差分離散示意圖：電場定義在單元的棱邊， 磁場定義在單元面中心Fig.1 Staggered finite difference discretization with electric fields on cell edges and magnetic fields placed on cell faces

我們采用交錯網格FDM對方程(1)進行離散化.如圖1所示，分別將電場和磁場分量定義在單元棱邊和單元面中心.采用矢量形式表示，則方程(1)離散形式可以表示為：

[C*C+diag(iωμσe)]e=0,

(2)

式中：e表示離散電場矢量，diag為對角矩陣，σe為單元棱邊的電導率(通過體積平均圍著棱邊的四個單元的電導率得到).C表示離散旋度算子，它將單元的棱邊上的矢量映射到單元的面上,C*是C的伴隨矩陣，表示將單元面上的矢量映射回到單元棱邊上(Egbert and Kelbert, 2012; Kelbert et al., 2014; Cherevatova et al., 2018).

將方程(2)簡化為如下矩陣形式的線性方程：

Ae=b,

(3)

式中A表示方程的系數矩陣，b表示右端源項.方程(3)可采用直接法或迭代法進行求解，一旦求解得到e，磁場矢量可以通過以下關系得到：

h=(-iωμ)-1Ce.

(4)

對于MT正演，其計算區域往往比較大，方程(3)中系數矩陣通常是大型稀疏的，采用直接求解法求解該方程需要耗費大量的計算時間和內存.因此，針對這類問題，往往采用迭代法進行求解(如本文中使用的BiCGstab).但是由于雙旋度算子存在豐富的零空間，迭代法在求解線性方程(3)的時候收斂速度較慢，為了提高計算效率，通常需要采用預條件技術.同時隨著ω的減小，數值解不能充分地模擬電導率不連續處的電荷積累，這也會造成迭代法的收斂速度變慢，這時需要通過強加散度校正來提高收斂速度，其具體形式如下：

(5)

2 預條件技術

通常情況下，構建一個矩陣P，稱之為預條件矩陣，將對于方程(3)的求解轉化為求解以下方程：

P-1Ae=P-1b.

(6)

通過這種轉換，可以有效降低系數矩陣A的條件數，相比于方程(3)，方程(6)更容易求解.在理想情況下預條件矩陣P取為A，式(6)直接可以得到電場的解.但是這時式(6)的預條件求解等效于式(3)的求解，失去了使用預條件技術的意義.實際應用中，我們通常采用更容易求解的P來近似A，比如常用的有SSOR、block ILU和 GS等.

多重網格法(MG)將最細網格上的殘差逐步投影到更粗網格上，在最粗網格上花更少的代價進行方程求解，然后將所求結果逐步插值到最細網格上對解進行校正，從而達到快速求解的目的.它主要包含有以下三個過程，首先在較細網格上進行少數幾次光滑迭代，消除高頻誤差；然后將低頻誤差投影到較粗網格上，細網格上的部分低頻誤差在粗網格上成為高頻成分，通過數次迭代可以有效剔除；重復以上過程直到最粗網格，這時最粗網格上未知數通常比較少，可以采用直接解法進行快速精確求解；最后從最粗網格將解逐級插值到細網格上以校正細網格的解，在每一次插值都需要進行數次平滑迭代以消除插值帶來的高頻誤差，直到最細網格.

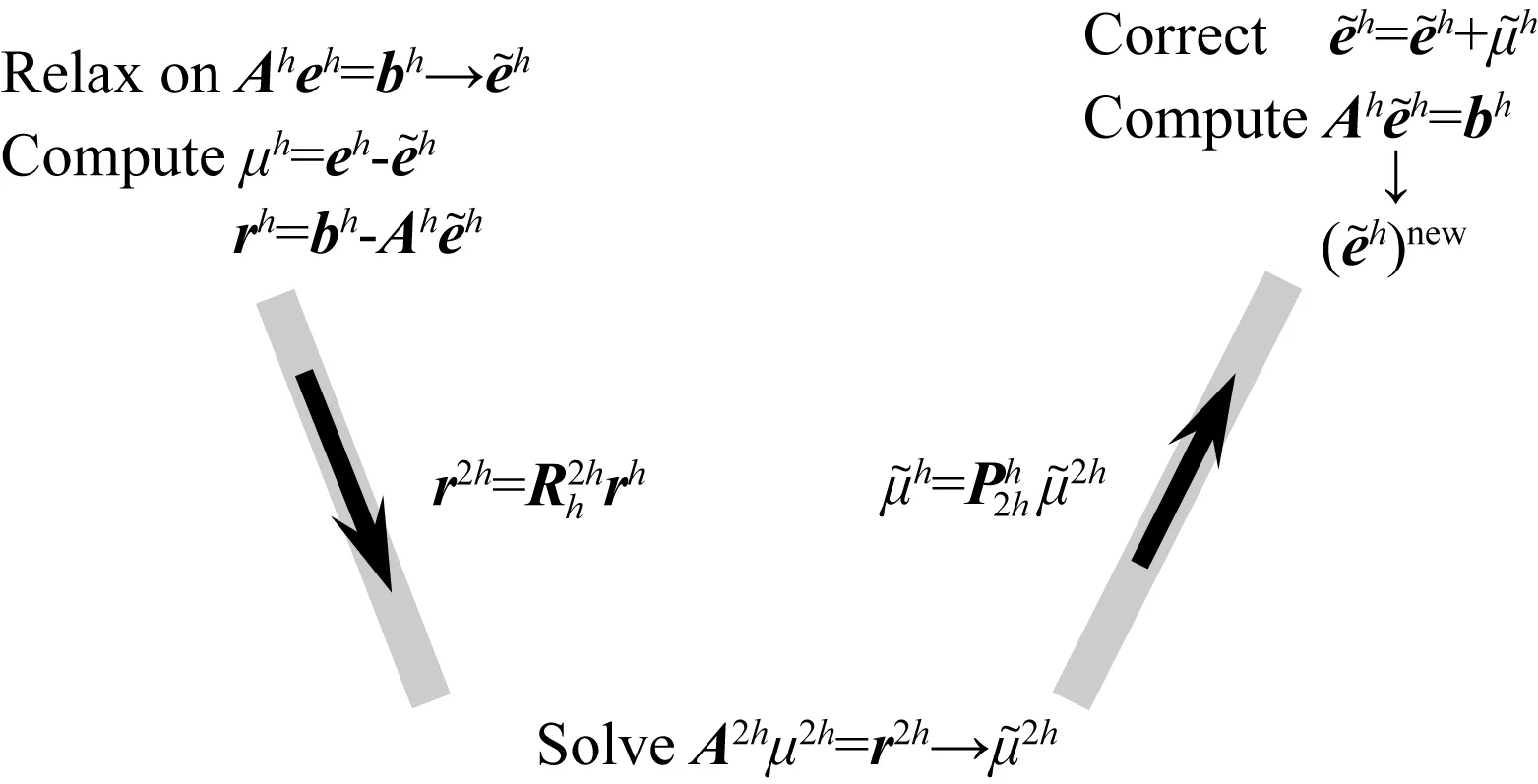
圖2 多重網格法迭代過程示意圖Fig.2 Diagram of iterative process of multigrid method

多重網格有多種循環方式(例如：V-循環，W-循環和F-循環)，根據求解問題的復雜程度可以選擇不同的循環方式，其中V-循環是最簡單的循環方式，后二者都是由V-循環嵌套而成.最為簡單的V-循環二重網格法有以下5個步驟(h和2h分別代表細網格和粗網格的步長)：

(5)后光滑：在插值過程中往往會引入新的誤差，因此還需要對方程Aheh=bh進行n2次光滑迭代以消除新的誤差.

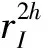
(7)

(8)

圖3 基于棱邊體積的加權限制算子的二維示意圖 (J?nsth?vel，2006)Fig.3 A two-dimensional schematic of the weighting restriction operator based on edge volumes (J?nsth?vel, 2006)

粗網格操作算子A2h產生采用文獻中的模塊思想(Egbert and Kelbert 2012; Kelbert et al., 2014; Cherevatova et al., 2018)，很容易產生粗網格上的方程(3)中的系數矩陣.平滑算法采用四色分塊GS算法(Li et al., 2020)，該平滑算法將所有節點分成四種顏色且相同顏色的每一節點相連接的分量組成的系統完全解耦(具有高度并行性)，可以同時進行更新.四色分塊GS算法在顏色間進行循環，當一種顏色更新完成后，相應的解可以作為下一種顏色更新的邊界條件.一旦獲得限制算子、插值算子、粗網格操作算子及平滑算法，我們就可以按照前面的流程進行多重網格計算.

3 數值計算

在這一節中，我們測試了GMG 預條件技術的正確性和效率.首先，設計了一個層狀模型，通過比較數值解和解析解來驗證該算法的正確性.然后，用一個經典的雙阻模型和一個國際標準模型從迭代次數和計算時間兩方面測試了算法的效率.我們的算法與傳統的預條件技術的BiCGstab求解器進行比較，包括GS、SSOR和block ILU.為了加速收斂，對于傳統預條件技術的 BiCGstab求解器，我們采用每40次迭代使用一次散度校正，而GMG預條件技術不需要散度校正.所有測試在AMD (R) 7-3700x 3.59 Hz的計算機上進行，當迭代到相對殘差小于等于10-10或達到1000次，迭代終止.

3.1 算法驗證

首先設計了一個一維層狀模型，該模型在電導率為200 Ωm的均勻半空間上方有一個電導率為100 Ωm的薄層，層厚2590 m.采用非均勻網格對64×64×128個單元進行離散，最小的網格單元為30 m×30 m×10 m，研究區域為7115 km×7115 km×2372 km.對于周期選取，我們在0.1～1000 s的范圍內采用對數間隔選取20個計算周期.分別使用解析法和數值法(求解器為GMG-BiCGstab)對模型進行計算得到視電阻率和相位曲線(圖4)，并求出相應的相對誤差.結果顯示：視電阻率和相位的最大相對誤差分別小于0.6%和0.4%(圖4c)，表明兩種方法得出的結果具有很好的一致性，驗證了本文提出的算法的正確性.

3.2 雙塊狀電阻率模型

為了進一步說明算法的準確性和高效性，在本小節我們設計了一個雙塊狀電阻率模型.如圖5所示：異常體的電阻率分別為10Ωm和1000 Ωm，尺寸大小均為20 km×20 km×20 km，埋深均為10 km，模型的背景電阻率為100 Ωm，其中最小單元的大小為2 km×2 km×2 km，網格數量為128×128×128(不包括空氣層)，正演模擬區域為281 km×281 km×311 km.我們選擇1、10、100、1000 s四個計算周期進行正演.

為了更好地驗證GMG預條件算法的正確性，在周期為100 s，我們對比了GMG預條件技術和傳統(例如：SSOR)預條件技術在兩種極化模式下的視電阻率和相位正演結果.如圖6所示：視電阻率的最大差異小于2×10-6，相位的最大差異小于1.5×10-6，說明兩者結果吻合得很好，也進一步驗證本文所提出的GMG預條件算法的正確性.

圖4 層狀模型GMG-BiCGstab與解析解的(a)視電阻率 和(b)相位對比及(c)相對誤差Fig.4 Comparison of the GMG-BiCGstab solution with analytic solution based on the layered model in terms of (a) apparent resistivity and (b) phase. (c) are the relative errors

圖7所示的是在不同周期下基于GMG預條件技術的BiCGstab在有、無散度校正(分別寫為GMG-DC和GMG)時的迭代次數和計算時間對比(每進行2次迭代計算執行1次散度校正).結果顯示有無散度校正對迭代次數無任何影響；散度校正需要消耗額外的計算時間，加散度校正反而會使計算時間顯著增加.由于GMG預條件技術采用了四色分塊GS平滑算法，它滿足局部電流散度為零，因此無需額外強加散度校正算法.

圖5 雙塊狀電阻率模型示意圖Fig.5 Diagram of two-block resistivity model

圖6 雙塊狀電阻率模型在周期為100 s時，不同求解器(GMG-BiCGstab與SSOR-BiCGstab) 在中心測線的視電阻率和相位的相對差異Fig.6 For the two-block resistivity model, the relative differences of apparent resistivity and phase along a middle survey line using different solvers (GMG-BiCGstab and SSOR-BiCGstab) at 100 s

圖7 GMG-BiCGstab法有、無散度校正的數值表現 (a)(c) x-極化模式； (b)(d) y-極化模式； (a)(b) 迭代次數； (c)(d) 計算時間.Fig.7 Numerical comparison of the GMG-BiCGstab method with and without divergence correction (a)(c) x-polarization mode; (b)(d) y-polarization mode; (a)(b) Iteration numbers; (c)(d) Compute time.

接下來將對比GMG、GS、block ILU、SSOR四種不同的預條件技術的數值表現，它們的迭代過程和計算時間對比結果分別如圖8—9所示.圖8結果顯示，對所有周期GMG預條件技術的迭代次數比其他預條件技術的迭代次數大大減少，GMG預條件技術基本在7次以內就能收斂.在傳統預條件技術中，SSOR效果最好.GMG預條件技術迭代次數基本和相對殘差的對數成線性關系，而傳統預條件技術隨著相對殘差的減少收斂會明顯變差.計算時間對比如圖9所示，對所有的周期，GMG預條件技術的計算時間遠遠少于其他預條件技術.相比其他方法，在x-極化模式下GMG預條件技術的計算時間減少了73%～90%，在y-極化模式下的計算時間減少了76%～88%.

3.3 DTM1模型

本小節我們將GMG-BiCGstab法應用于求解一個更復雜的Dublin模型1(DTM1)(Miensopust et al., 2013).如圖10所示，在均勻半空間(100 Ωm)中，存在三個埋深、尺寸、電阻率均不同的異常體，異常體的參數如表1所示.我們將模型均勻剖分，單元的尺寸均為2.5 km×2.5 km×2.5 km，網格數量為128×128×128(不包括空氣層)，總的區域為320 km×320 km×320 km.與3.2節一樣，我們采用的周期為1 s、10 s、100 s和1000 s.

圖8 雙塊狀電阻率模型使用不同預條件技術的BiCGStab在不同周期的收斂過程 (a)(b)(c)(d) x-極化模式； (e)(f)(g)(h) y-極化模式.Fig.8 The convergence process of BiCGStab using different preconditioners for different periods based on the two-block resistivity model (a)(b)(c)(d) x-polarization mode; (e)(f)(g)(h) y-polarization mode.

圖9 雙塊狀電阻率模型使用不同預條件技術的 BiCGStab在不同周期段內的計算時間對比圖 (a) x-極化模式； (b) y-極化模式.Fig.9 Comparison of computer time of BiCGStab using different preconditioners for different periods based on the two-block resistivity model (a) x-polarization mode; (b) y-polarization mode.

表1 DTM1 模型中異常體在三個方向的大小Table 1 The anomalies size in three directions for DTM1

針對該模型，在周期為100 s，我們對比了GMG-BiCGstab的正演結果和MTNet(http:∥www.mtnet.info/workshops/mt3dinv/2008_Dublin/dublin_forward.html)提供的正演結果，MTNet結果由不同的算法(Mackie et al., 1994; Siripunvaraporn et al., 2002; Farquharson et al., 2002; Nam et al., 2007)得到.結果顯示，我們的結果與MTNet的結果基本吻合，進一步驗證本文提出的算法的正確性.

GMG預條件技術和三種傳統預條件技術(GS、block ILU和SSOR)的迭代收斂過程如圖12所示，結果顯示收斂過程對比與前一模型的對比結果相似.對所有周期，GMG預條件技術迭代次數與相對殘差的對數成線性關系，其他預條件技術隨著相對殘差的減小收斂明顯變差.GMG預條件技術收斂需要的迭代次數遠遠小于其他三種傳統的預條件技術.不同預條件技術收斂需要的計算時間如圖13所示，對于所有周期，GMG預條件技術的耗時遠遠小于其他預條件技術.其中，在周期為1000 s時，GMG預條件技術在x-極化模式下的計算時間相對GS減小84%(188 s vs.1245 s)，相對block ILU減小83%(188 s vs.1131 s)，相對SSOR減小79%(188 s vs.926 s).y-極化模式下計算時間相對GS減小84%(175 s vs.1119 s)，相對block ILU減小83%(175 s vs.1089 s)，相對SSOR減小78%(175 s vs.825 s).

圖10 DTM1模型示意圖 綠色、藍色和紅色分別表示電阻率為10 Ωm、1 Ωm和10000 Ωm的異常體.背景電阻率為100 Ωm.Fig.10 2D view of the DTM1 model Green,blue and red represent 10 Ωm, 1 Ωm and 10000 Ωm, respectively with background conductivity of 100 Ωm.

圖11 DTM1模型在周期為100 s時，中心測線的響應對比 (a)(c) x-極化模式； (b)(d) y-極化模式； (a)(b) 視電阻率； (c)(d) 相位.Fig.11 Based on the DTM1 model, the response comparison along a middle survey line at period of 100 s (a)(c) x-polarization mode; (b) (d) y-polarization mode; (a)(b) Apparent resistivity; (c) (d) Phase.

圖12 DTM1模型使用不同預條件技術的BiCGStab在不同周期的收斂過程 (a)(b)(c)(d) x-極化模式； (e)(f)(g)(h) y-極化模式.Fig.12 The convergence process of BiCGStab using different preconditioners for different periods based on the DTM1 model (a)(b)(c)(d) x-polarization mode; (e) (f)(g)(h) y-polarization mode.

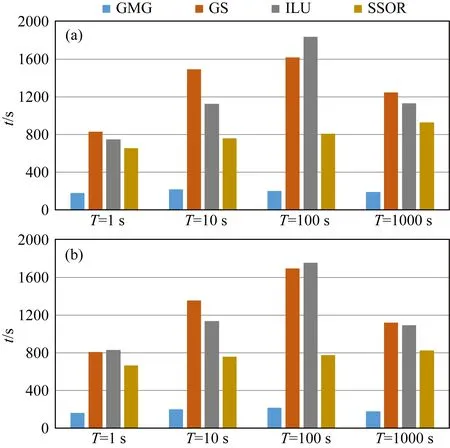
圖13 DTM1模型使用不同預條件技術的BiCGStab 在不同周期的計算時間對比圖 (a) x-極化模式； (b) y-極化模式.Fig.13 Comparison of computer time of BiCGStab using different preconditioners for different periods based on the DTM1 model (a) x-polarization mode; (b) y-polarization mode.

4 結論

3D MT 在礦產資源勘探和科學研究等領域中發揮著越來越重要的作用，但是對于覆蓋范圍大的MT測量數據，進行全區的3D反演仍然非常具有挑戰性，需要提高大規模3D MT正演模擬的計算效率.為此，本文提出了一種高效的GMG預條件技術用于3D MT FDM正演模擬.GMG將細網格上的大型稀疏方程求解通過若干次簡單平滑迭代逐次轉化到更粗網格上以更小的代價進行高效求解，特別適合大型稀疏矩陣的求解.該預條件技術的平滑算法采用四色分塊GS法，滿足局部電流散度為零，避免了散度校正的使用.通過設置一個簡單層狀模型驗證了本算法的正確性，然后設置一個雙塊體電阻率模型和一個國際標準DTM1模型，基于BiCGStab，通過與傳統的預條件技術(GS、block ILU、SSOR)進行對比測試了本文所提出算法的數值表現.

結果顯示GMG預條件技術在所有的測試實例中具有比較穩定的數值表現，相對殘差的對數隨著迭代次數的增加呈線性衰減，而傳統預條件技術隨著相對殘差的對數減小收斂明顯變慢.傳統預條件技術的計算效率往往隨著周期變長明顯變差，而GMG預條件技術的收斂速度不隨周期的變長而變慢.對本文所有實例，GMG預條件技術所耗費的計算時間明顯小于傳統預條件，比傳統預條件技術減少最少73%以上.以上結果顯示本文提出的GMG預條件技術具有很好的數值表現，適合應用于大型3D MT正演計算.

致謝作者感謝美國俄勒岡州立大學Gary D. Egbrt教授對我們的論文工作提供了很多有意義的討論和建議，同時也向三位匿名審稿專家以及本文的編輯提出的寶貴修改意見表示衷心的感謝.