改進的小波包雙參數(shù)雙閾值降噪方法

李偉 李林

（銅陵學院，安徽 銅陵 244061）

一、引 言

在現(xiàn)代電子測量和傳感測試領域中，采集到的數(shù)據(jù)經常無法避免地被各種噪聲所干擾。為了提高特征提取的準確度，對采集到的數(shù)據(jù)進行降噪處理是很有必要的。小波包變換是一種具有時頻域、多分辨率等特性的信號處理方法，非常適合用于消除非平穩(wěn)噪聲。目前基于小波包變換的降噪方法包括模極大值法、空域相關濾波法和閾值法等。其中，小波包閾值降噪法理論簡單、可實行性高且在工業(yè)現(xiàn)場被廣泛應用。

從提出到現(xiàn)在，已有許多學者對小波閾值去噪法做了深入的研究，其中最為經典的是Donoho等[1]提出的軟、硬閾值函數(shù)去噪法。雖然這兩個函數(shù)具有一定的去噪效果，但也存在許多不足之處。針對其不足，國內外很多學者相繼提出了一些改進的閾值去噪函數(shù)[2-3]。這些函數(shù)雖然在一定程度上兼顧了軟硬閾值函數(shù)的特點，但也存在一些如函數(shù)閾值選取相對固定、函數(shù)缺乏靈活性等不足。針對上述問題，文獻[4]提出了一種小波雙閾值雙因子函數(shù)。該函數(shù)通過引入雙閾值和可變因子，使其能通過改變參數(shù)值來調節(jié)降噪幅度。但研究發(fā)現(xiàn)，該閾值函數(shù)不能根據(jù)實際信號中的噪聲能量分布來局部調整降噪程度，從而導致降噪效果不太理想。本文丟掉可變因子，引入新的調節(jié)參數(shù)和函數(shù)模型，以期改進后的閾值函數(shù)能夠根據(jù)實際信號中有用信號和噪聲信號的分布來整體和局部的調整函數(shù)的降噪幅度。改進后的閾值函數(shù)亦連續(xù)且抑制了恒定偏差。最后通過仿真和實驗信號，比較不同小波閾值去噪法的信噪比和均方誤差，驗證本文方法的有效性。

二、傳統(tǒng)與現(xiàn)有閾值降噪方法

w是原始信號小波包分解后的系數(shù)，T是閾值，η(w)是閾值函數(shù)處理后的小波包系數(shù)。

(一)傳統(tǒng)雙閾值法

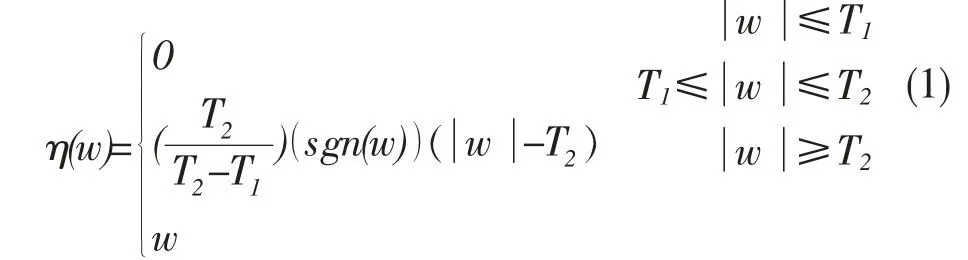
傳統(tǒng)雙閾值函數(shù)克服了函數(shù)不連續(xù)的問題，并有效地抑制了處理后小波包系數(shù)之間的恒定偏差。但該方法對大于上閾值的部分不做任何處理，可能導致去噪不干凈的情況發(fā)生。

(二)文獻[4]的閾值法

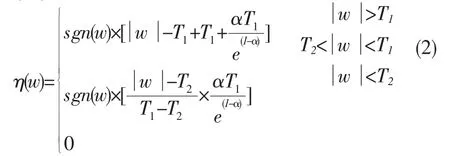
式中，T1、T2分別為上、下閾值，β為關聯(lián)參數(shù)。α可以用于調整閾值函數(shù)整體降噪程度，在(0,1)之間取值。該函數(shù)克服了函數(shù)不連續(xù)和恒定偏差的不足，并可以通過改變調節(jié)參數(shù)來調整降噪幅度和降噪區(qū)間。但它不能根據(jù)實際信號的噪聲能量分布，自適應地調整整體和局部的降噪幅度。

三、改進的小波包雙閾值函數(shù)

（一）新閾值變換函數(shù)

（1）閾值函數(shù)表達式

根據(jù)上節(jié)討論，對小波包系數(shù)w來說，閾值函數(shù)均為奇函數(shù)。設Cmin、Cmax分別表示小波包系數(shù)w絕對值的最小和最大值。參考文獻[5]中閾值降噪函數(shù)條件：

1.在函數(shù)定義域范圍內具有單調性且無間斷點。

2.在定義域范圍內，導函數(shù)值逐漸增大，或者先增大再減小，這樣才能使小波包系數(shù)中間區(qū)域的系數(shù)差異增大，便于識別。

3.導數(shù)（尤其是區(qū)間[Cmin,Cmax]中段的導數(shù)）應大于1。

根據(jù)文獻[5]中閾值函數(shù)條件和文獻[4]中閾值降噪方法的不足，本文在此基礎上，定義了下式所示的雙參數(shù)雙閾值函數(shù)：

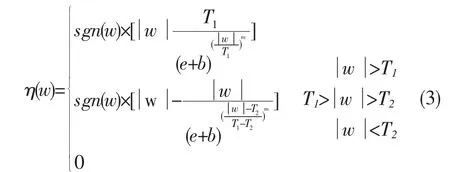
式中，下閾值T2=βT1＜T1；β(0＜β＜1)為閾值關聯(lián)參數(shù)。m、b為本文引入的新的調節(jié)參數(shù)。下面來證明，新閾值函數(shù)不僅滿足以上條件，而且具有獨特性質。

（2）改進的閾值函數(shù)分析

函數(shù)的性態(tài)包括連續(xù)性、單調性、漸進性及凹向等。

1)函數(shù)連續(xù)性

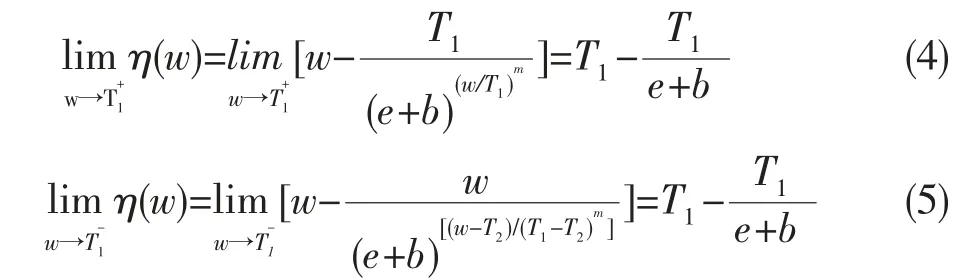
由式(4)～(6)可知，閾值函數(shù)η(w)在閾值T1、T2處連續(xù)。

2)函數(shù)單調性

當T1＞w＞T2時，設w1＜w2

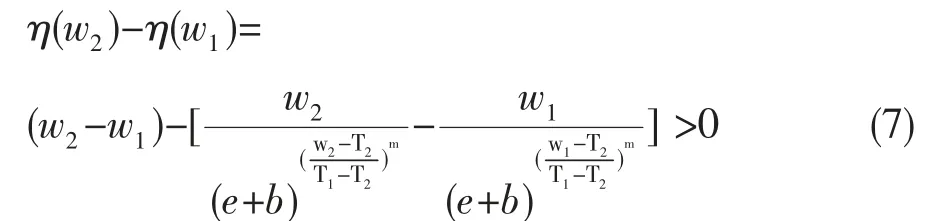
同理，當w＞T1時

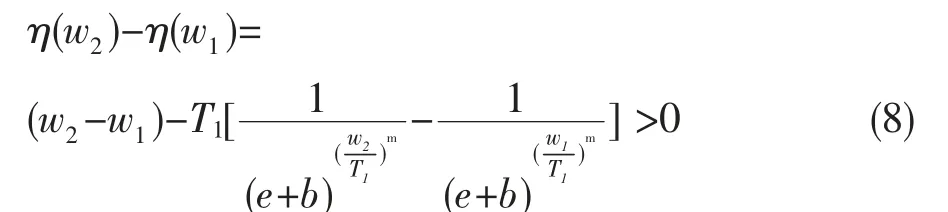
式(3)是奇函數(shù)。由上述函數(shù)單調性證明得，本文閾值函數(shù)在定義域范圍內單調遞增。故本文閾值函數(shù)符合條件(1)、(2)。

3)漸近性

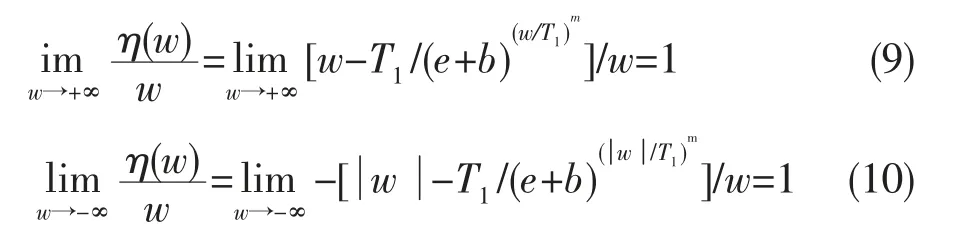
由上述函數(shù)推導得，本文閾值函數(shù)以y=x為漸近線。與閾值變換函數(shù)的條件(3)相符。

4）導函數(shù)性態(tài)

由于本文閾值函數(shù)是奇函數(shù)，故下面在[0,+∞)內驗證本文閾值函數(shù)導函數(shù)特性。

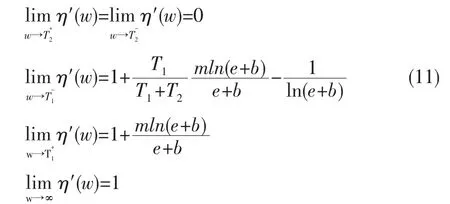
由式(11)得，當m較大時，式(3)的導函數(shù)在T1處的導數(shù)值大于1。除此之外，式(3)在各閾值區(qū)間內均是初等函數(shù)組成，因此本文閾值函數(shù)在個閾值區(qū)間內導函數(shù)連續(xù)，并以為漸近線。因此，改進后的閾值函數(shù)在[T1，+∞)內導函數(shù)均大于1。故本文閾值函數(shù)符合上述條件(3)。

5)函數(shù)偏差性

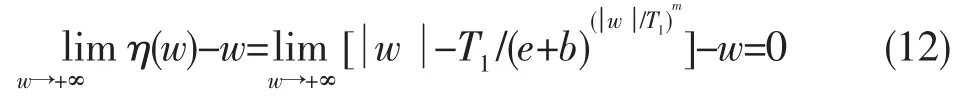
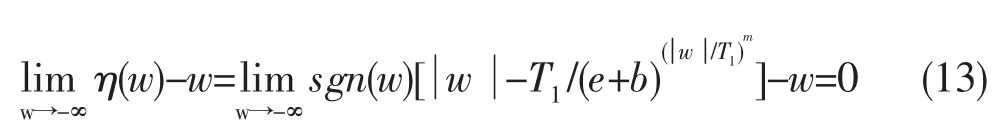
由閾值函數(shù)的恒定偏差性證明得，當本文w值趨向于無窮時，η(w)=w。故本文提出的改進后的閾值函數(shù)無恒定偏差。

由上述分析可知，改進后的閾值函數(shù)在基本滿足閾值去噪變換的條件下，繼承了文獻[4]函數(shù)在閾值點連續(xù)及無恒定偏差的優(yōu)點。

6)調節(jié)參數(shù)m與b影響分析

此部分參數(shù)影響分析，令下閾值T2=5，上閾值T1=12。通過控制變量法，調節(jié)m與b的值來研究相應閾值函數(shù)降噪幅度的影響。結果如圖1所示。

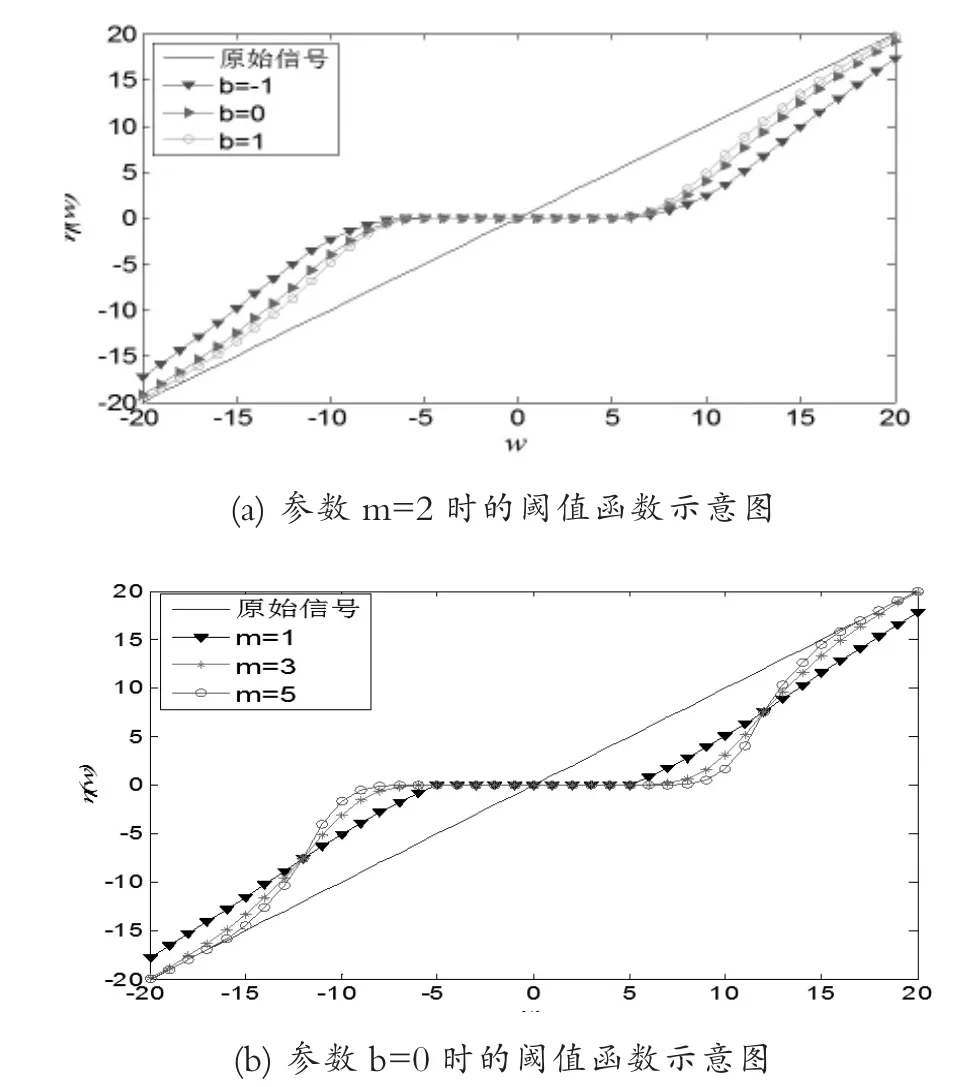
圖1 改進閾值函數(shù)示意圖

由圖1（a）可見，m值不變的情況下，b越大降噪幅度越小；反之，降噪幅度越大。由圖1（b）可見，b值不變的情況下，m越大函數(shù)在不同閾值范圍內變化越明顯，從而對大于和小于閾值的部分極大程度地保留和收縮，實現(xiàn)有用信息和噪聲信息的分離。反之，降噪幅度越小。

（二）閾值及調節(jié)參數(shù)的確定

(1)參數(shù)m的確定

參數(shù)m主要反映不同小波包的能量分布。為了進一步提高方法的自適應性，對函數(shù)表達式中參數(shù)m進行數(shù)學建模為：

式中，mj,k表示小波包分解第j層中第k段小波包系數(shù)的調節(jié)系數(shù)。Ej,k是小波包系數(shù)的能量，表達式為。Ej是小波包總能量，表達式為Ej=

實際工況下，噪聲能量一般大于有用信號，因此，Ejk/Ej值一般較小。另外，由式(3)和圖(1)可知，1＜m＜5。綜合考慮，m0=1，α=10。

(2)上下閾值的確定

文獻[4]中指出利用sqtwolog準則選取的閾值一般偏大的特點。除此以外，現(xiàn)有閾值選取準則，均存在自身的不足。針對現(xiàn)有方法的特點，文獻[6]指出：采用sqtwolog準則選取上閾值T1，再通過T2=βT1(0＜β＜1)確定下閾值能盡可能地保留有用信號。但閾值關聯(lián)參數(shù)?應和調節(jié)因子b一起遍歷選取，以達到最好的降噪效果。

(3)參數(shù)b的取值范圍

由式(3)可知，為了對小波包系數(shù)實現(xiàn)收縮作用，分母(e+b)應大于1。但數(shù)值試驗表明：若(e+b)過大，反而降噪效果較差。因此，本文選定參數(shù)b在[-1.5，1.5]之間取值。對于不同信噪比的信號，若參數(shù)b的取值跨度較大，易造成降噪不充分或過度降噪的情況，相反跨度較小，雖避免了上述情況，但會極大地增加計算量。

(4)參數(shù)b和系數(shù)k的聯(lián)合確定

本文首先通過sqtwolog準則確定上閾值T1的值。其次根據(jù)式(14)確定實際信號經小波包分解后每頻段能量分布系數(shù)m。最后，以降噪后信號的最大信噪比為目標函數(shù)，在b和k的調節(jié)范圍內，選擇最佳的b和k的參數(shù)組合。具體方法如下：

(1)在b和k的取值范圍內，選擇合適的步長△b和△k，并以此分別將對應區(qū)間等分成M和N份。

(2)由步驟(1)得到一個參數(shù)矩陣D，其包含M×N個數(shù)據(jù)點。每個數(shù)據(jù)點代表一種b和k的組合。遍歷該矩陣中的每個數(shù)據(jù)點，利用式(3)進行降噪，以最大信噪比作為目標函數(shù)[7]確定最佳參數(shù)組合。

四、仿真與試驗驗證

文獻[4]中的閾值函數(shù)通過引入雙調節(jié)因子，使其能夠靈活地調整函數(shù)降噪幅度。但其忽略了小波分解后能量分布的影響，針對這一點，本文在其基礎上進行改進。基于此，本節(jié)欲通過仿真和試驗信號驗證改進后閾值函數(shù)的有效性。

（一）仿真信號驗證

首先通過Matlab軟件仿真沖擊信號(bumps)，并由wnoise函數(shù)對仿真信號添加不同程度高斯白噪聲，以仿真不同信噪比的原始信號。然后采用傳統(tǒng)雙閾值法、文獻[4]中的閾值方法和本文提出的閾值方法對不同信噪比的仿真信號進行降噪處理。最后計算不同方法降噪重構后對應信號的信噪比(SNR)和均方誤差(RMS)。

以SNR=3的沖擊信號為例，不同方法降噪重構后的信號分別如圖2所示。

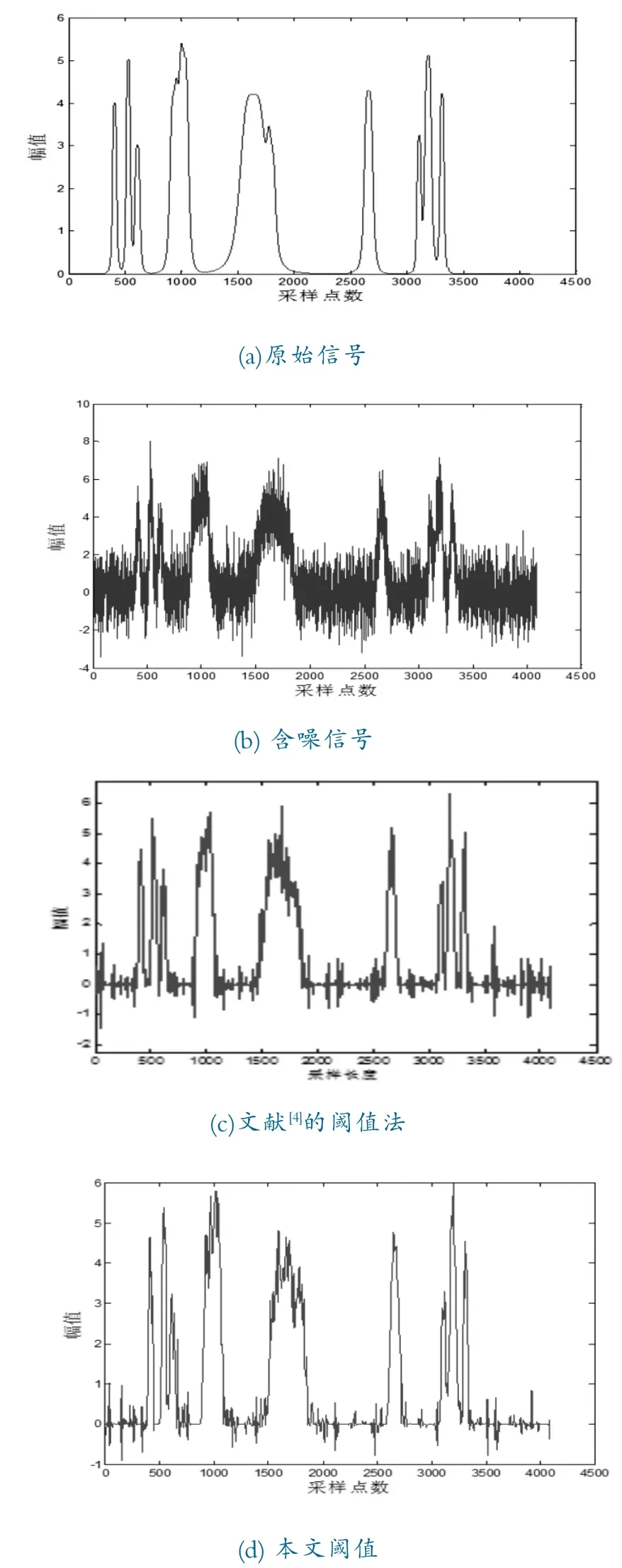
圖2 仿真信號降噪效果圖

由圖2(a)和圖2(b)可見，在SNR=3的信噪比下，原始沖擊信號(bumps)的沖擊特征已基本被淹沒。由圖2(c)可見，文獻[4]中的雙閾值法能有效地降低噪聲對沖擊特征的影響，但仍出現(xiàn)大面積的信號震蕩現(xiàn)象，且信號突變部分的處理較為粗糙。由圖2(d)可見，改進后的閾值函數(shù)的降噪效果要明顯優(yōu)于文獻[4]的方法。另外，比文獻[4]的方法更有效地抑制了信號震蕩現(xiàn)象，震蕩幅度更小且突變部分處理較好。

為進一步研究不同信噪比下本文閾值函數(shù)的降噪效果，采用不同信噪比的仿真信號，對比計算不同方法降噪后的信噪比和均方誤差，計算結果如下表1、2所示。

表1 不同閾值函數(shù)去噪后信噪比

由表1和表2可見，無論是去噪后信號的信噪比還是均方誤差，通過本文提出的新閾值函數(shù)處理后的信號均優(yōu)于傳統(tǒng)降噪方法。與圖2的分析結果相同。

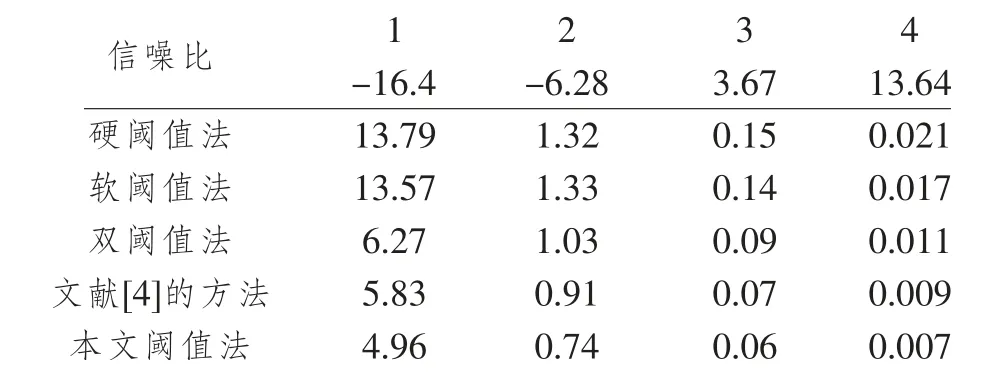
表2 不同閾值函數(shù)去噪后均方誤差

（二）試驗信號驗證

本節(jié)統(tǒng)一選取行星齒輪箱太陽輪裂紋故障實驗信號為分析對象。實驗內容、步驟、故障設置及信號采集過程等如文獻[8]所述。利用不同降噪方法對加噪信號進行降噪處理，并計算每種方法降噪重構后信號的信噪比，結果如表3所示。

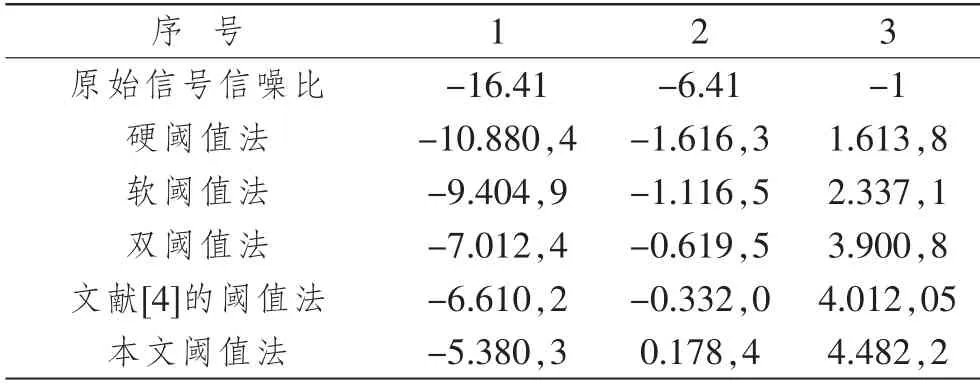
表3 不同降噪方法去噪后信噪比

由表3可見，在不同信噪比情況下，相比于其他降噪方法，改進后的閾值法降噪后信號的信噪比更高，即降噪效果更明顯。進一步驗證了本文提出的閾值方法的有效性。

五、結論

現(xiàn)有的閾值函數(shù)已函數(shù)連續(xù)且無恒定偏差，且通過改變調節(jié)因子大小改變函數(shù)降噪程度，但其不能根據(jù)實際信號中噪聲能量的分布自適應地調整不同頻段的降噪幅度，故而降噪效果不夠理想。針對這一問題，本文引入了兩個新的調節(jié)參數(shù)，提出了一種雙參數(shù)的雙閾值函數(shù)。改進后的閾值函數(shù)在基本滿足閾值變換的條件下，亦函數(shù)連續(xù)且無恒定偏差。另外，函數(shù)通過調節(jié)新的調節(jié)參數(shù)b和m值，使改進后的函數(shù)能夠根據(jù)實際信號中的不同頻段內噪聲及有用信號的能量分布，自適應的調整函數(shù)整體和局部的降噪幅度。最后利用仿真和試驗信號，對比驗證了改進后閾值方法的有效性。