一種基于因果關系的慣性制導工具誤差系數分離方法

魏宗康,郭鎮凈

（北京航天控制儀器研究所,北京 100039)

0 引言

命中精度作為彈道導彈的一項重要戰技指標,受到的影響因素很多,比如制導方法誤差、制導工具誤差、引力異常、再入誤差等。其中,慣性制導工具誤差約占整個命中精度誤差的60%～80%[1]。因此,建立易于分離的、精確的制導工具誤差模型并給出高精度參數估計方法,是提高導彈精度的關鍵[2]。

傳統的制導工具誤差是基于速度域上的線性回歸模型進行估計的,由于環境函數矩陣各列之間的復線性問題,導致利用最小二乘法并不能得到準確的估計。為解決該問題,現有文獻提出了兩類方法:1)使用Bayes估計,這種方法最大的缺點就是對驗前信息依賴性太強,估計結果可能會不準確;2)使用主成分估計、嶺估計、偏最小二乘估計等不同的估計方法,這些方法的核心思想是在模型不降階的前提下估計出系數的近似解,帶來的問題就是估計有偏差[1,3-5]。但是,這些方法都沒有從根本上解決慣性制導工具誤差系數的精確分離問題。

本文針對該問題提出了一種基于因果關系的慣性制導工具誤差分離方法,研究內容不再是估計每個系數,而是估計不同相關系數之間組合后的值,采用該方法得到的分離結果更準確。

1 制導工具誤差模型及分離難點

制導系統工具誤差模型為

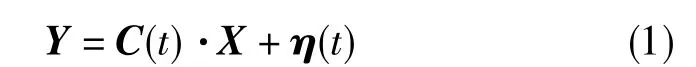
式（1)中,Y為遙外測觀測輸出量,C（t)·X 為Y的主值函數,Y與C（t)·X之差η（t)稱為殘差。

制導工具誤差分離是采用某種手段以便從制導工具誤差模型中求解出制導工具誤差系數向量的值,最簡單直觀的手段是基于最小二乘來估計工具誤差向量,即

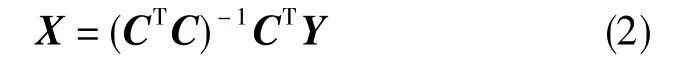
但由于慣性系統誤差的環境函數間強線性相關,即結構矩陣C的各列之間存在嚴重的復共線性,致使信息矩陣Φ=CTC有一些很接近于0的特征值,即Φ=CTC病態,導致用最小二乘估計誤差大,分離結果不可信,達不到誤差分離的目標。

下面給出實例來具體說明傳統方法的不足及本文方法的計算過程和優點。設慣性制導線性系統的歸一化系數真值X的各元素為1,由于制導數據量過于龐大,截取其中一小段構成的環境函數結構矩陣C和遙外測觀測輸出量Y為

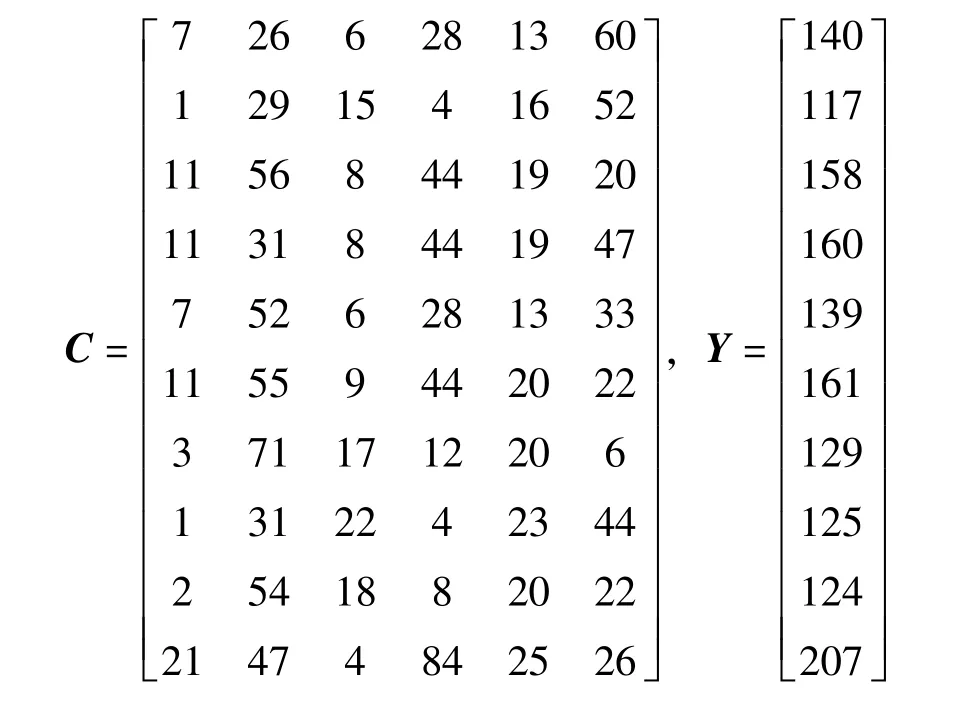
可以驗證,Φ=CTC的秩為4,Φ為奇異矩陣。此時,采用式（2)將不能解出X的值。

2 基于因果關系相關系數的辨識方法

為了解決環境函數矩陣不為列滿秩時的求解問題,提出了主成分估計（Principal Component A-nalysis,PCA)、Bayes估計、嶺估計、環境函數矩陣抖動估計、選主元剔次元估計、偏最小二乘估計[1,3,5-7],試圖使誤差分離結果更準確。

2.1 主成分估計

當C不為列滿秩時,則不能用式（2)的最小二乘法求解。所謂主成分估計,就是把信息矩陣Φ=CTC中較小的特征值近似簡化為0以改善矩陣病態,然后求解X的過程。

對信息矩陣進行特征值分解,存在正交變換矩陣P= [PAPB],滿足

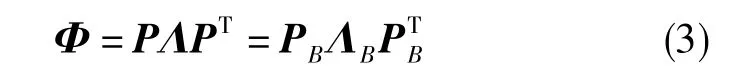
式（3)中,Λ為特征值構成的對角陣,ΛB為Λ中所有非零特征值構成的對角陣,PA為零特征值對應的P中的特征向量,PB為非零特征值對應的P中的特征向量。

誤差系數的主成分估計值為

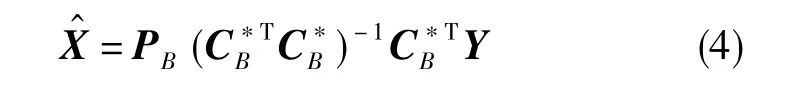
采用上述主成分法對實例求解,非零特征值對應的特征向量及非零特征值矩陣分別為

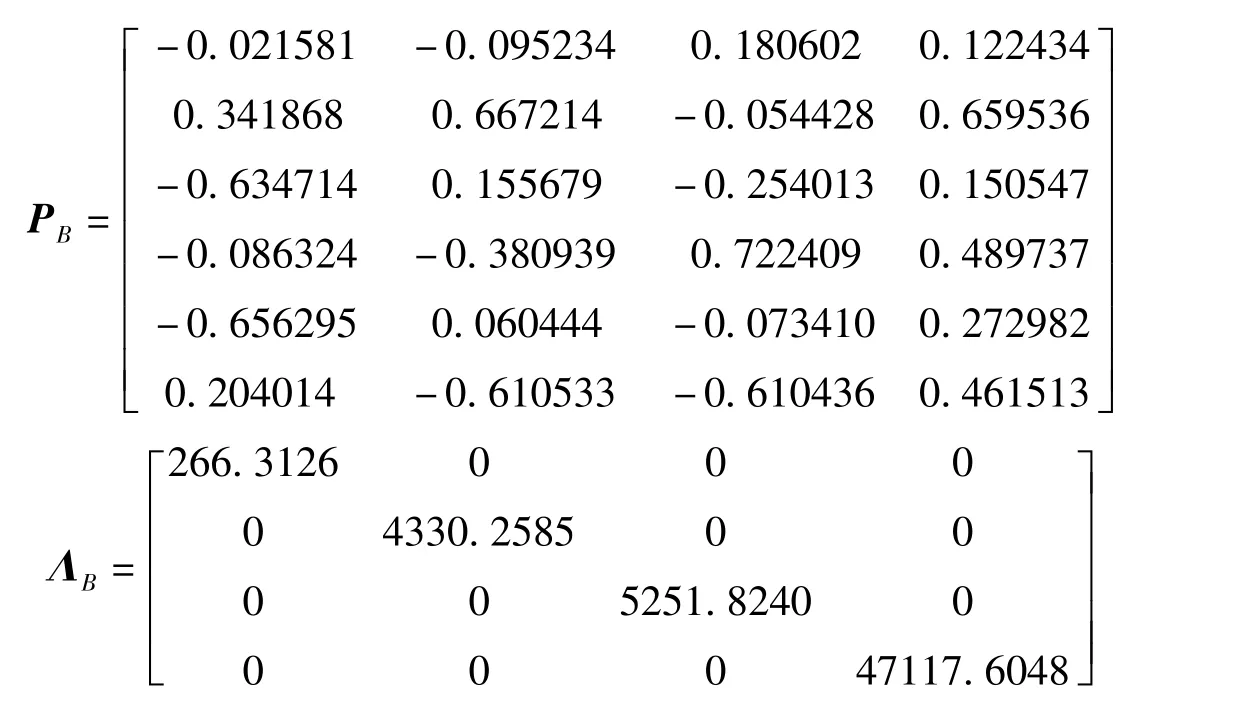
誤差系數的計算值及誤差為

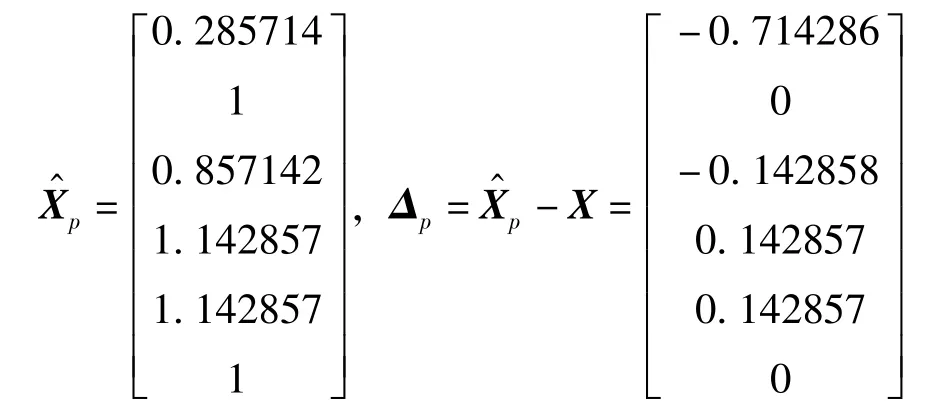
可以看出,不能求解出X的真值。

2.2 Bayes估計

Bayes估計（又稱為約束主成分估計)的關鍵是考慮誤差系數的驗前信息。假設所有誤差系數均服從正態分布,驗前均值為X0,驗前方差矩陣為,則Bayes估計的計算公式[7]為

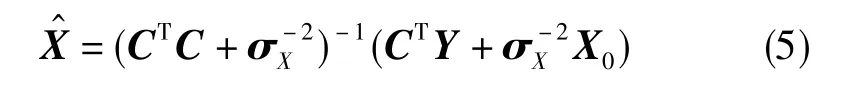
因此,Bayes估計在理論上存在不足之處,對驗前信息依賴性較強,若驗前信息不可靠時,估值結果也不可信[5,7]。

2.3 嶺估計

嶺估計的工作原理是構造新的信息矩陣Φ′,使得其最小特征值距零點遠一些,從而改進計算性能。嶺估計的計算公式為

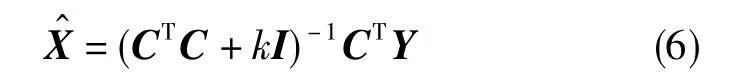
嶺參數k的大小決定了對條件數改造的程度大小。因此,如何選擇合適的k值成為嶺估計研究的重心。

對于實例,設k的值由2×10-8逐漸增大到7,信息矩陣Φ′的條件數大幅改善,由2.35×1012減小到6.73×103,如圖1所示。

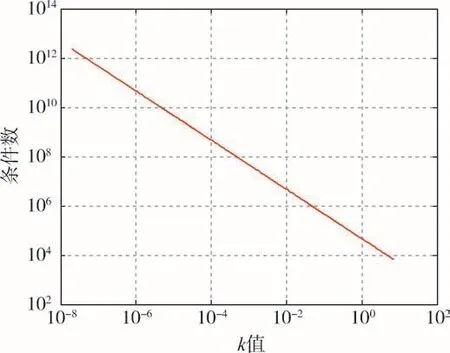
圖1 不同k值對應的信息矩陣Φ′的條件數Fig.1 Condition number of information matrix Φ′corresponding to different k

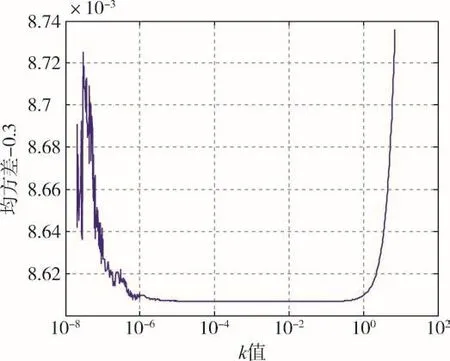
圖2 不同k值對應的均方誤差值Fig.2 Mean square error corresponding to different k

可以看出,當k的值在10-4～10-2區間內時,均方差相對較小。設k=1×10-3,計算值及估計誤差為

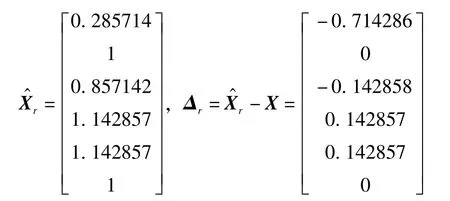
與主成分估計值進行比較,二者近似相等。

但在工程應用中,并不知道真實值X的大小,k的取值具有一定的主觀隨意性,缺乏理論嚴謹性。但最根本的問題是,仍然沒有克服估計的偏差性。

2.4 環境函數矩陣抖動估計

環境函數矩陣抖動估計的基本思想是對矩陣C做微幅抖動處理

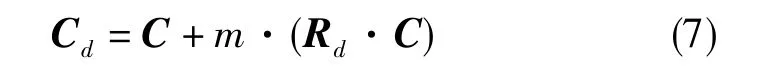
式（7)中,Rd為一個大小與矩陣C相同的隨機矩陣, 其每個元素 Rd（i,j)～U（-1,1); （Rd·C)為矩陣Rd與矩陣C的點乘;m為抖動的幅度控制參數。

對變化后的回歸模型Y=CdX進行最小二乘估計,結果為

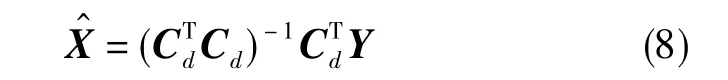
對于實例,設m的值由1×10-7逐漸增大到0.1,信息矩陣Cd的條件數大幅改善,由2.53×1016減小到3.33×104,如圖3所示。

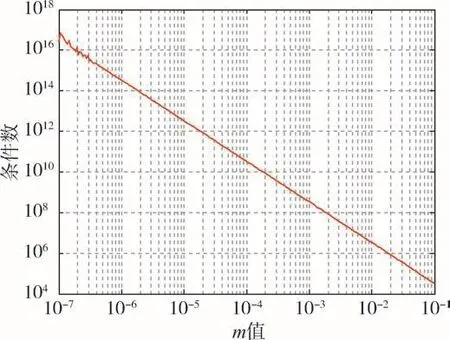
圖3 不同m值對應的信息矩陣Φ′的條件數Fig.3 Condition number of information matrixΦ′corresponding to different m

由圖4可知,當m的值在10-7～10-6區間內時,抖動效果不明顯,主要原因是信息矩陣Cd不滿秩。當m的值在10-6～10-1區間內時,信息矩陣Cd滿秩,當m=1×10-6時,計算值及誤差為

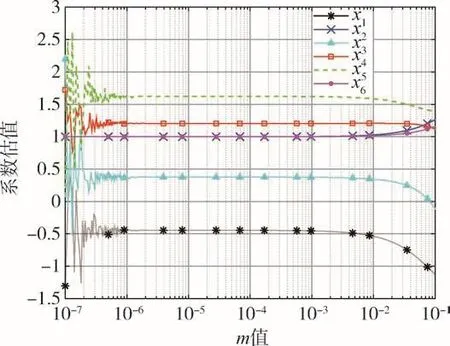
圖4 不同m值對應的系數估計值Fig.4 Coefficient estimationcorresponding to different m

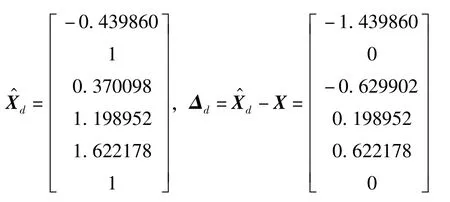
但估計效果不理想,均方差接近0.69（大于主成分估計和嶺估計的結果)。因此,可以得出結論,采用環境函數矩陣抖動估計計算的值準確性不如主成分估計和嶺估計的結果,但三者都不能估計出真值。

2.5 選主元剔次元估計

主成分估計、嶺估計、環境函數矩陣抖動估計等方法的一個特點是估計過程沒有改變結構矩陣的維數,辨識參數的維數也保持不變,但存在的問題是估計不準確。另外一個思路是改變結構矩陣的維數,對模型進行降維。選主元最小二乘法就是通過剔除接近零的最小特征值對應的環境函數矩陣的列以改進數據處理的效果,即選主元、剔次元。

由于選主元最小二乘法與顯著性的思路類似,下面采用該方法對實例進行求解。表示因果關系的方程為

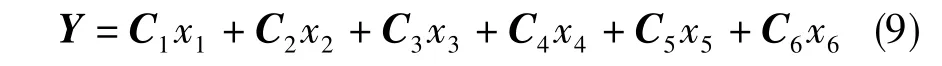
由于信息矩陣CTC為奇異矩陣,對原矩陣依次采用兩次環境函數矩陣抖動給出預估值,并進行顯著性分析,逐次去掉不顯著的系數x5和x4。之所以去掉x5,是因為C5x5對Y的貢獻度最小,如圖5所示。

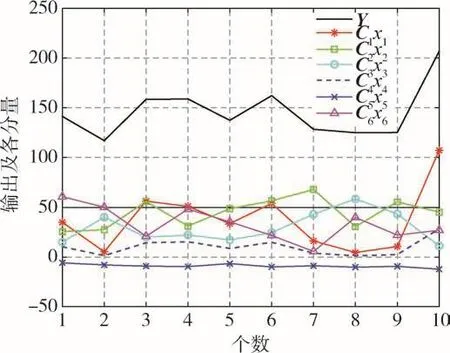
圖5 輸出值及各項系數xi對應的分量CixiFig.5 Output value and component Cixi corresponding to each coefficient xi

第三次估計值時,由于信息矩陣為滿秩,不能采用環境函數矩陣抖動法,故直接采用最小二乘法給出各項系數xi的值。為方便起見,設不顯著的系數為0,即x4=0、x5=0,求得的系數及誤差為

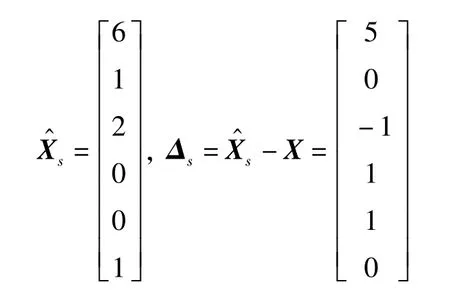
該估計值雖然可以滿足Y=CX,但估計的結果與真值差別較大。

2.6 偏最小二乘估計

偏最小二乘回歸方法的思路為:

1)設S0=C、Y0=Y,在S0中提取成分t1,令t1=S0·w1。 其中,w1=ST0Y0/‖Y0‖。 實施 S0與Y0在t1上的回歸

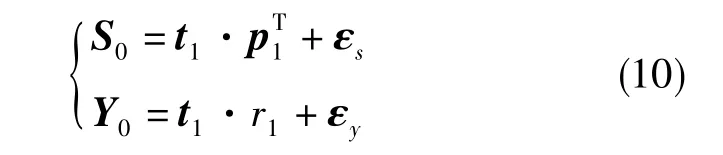
式（10)中,向量 p1、標量 r1為回歸參數,εs與εy為回歸殘差,有

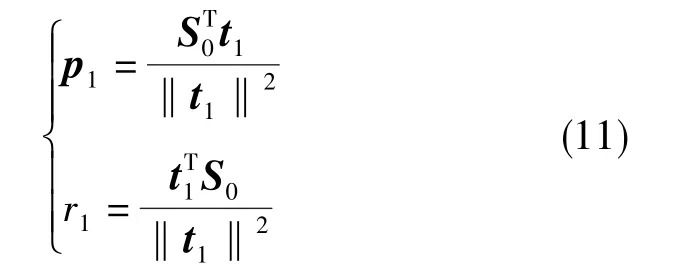
記殘差矩陣S1=S0-t1,Y1=Y0-t1r1。如果此時回歸方程已經達到滿意的結果,則算法停止;否則,令S0=S1,Y0=Y1,對殘差矩陣進行新的成分提取與回歸。

2)在第h步（h=2,3,…,m),方程滿足精度要求,這時得到k個成分t1、t2、…、tk。其中,

可以看出,此處得到的結果與主成分估計、嶺估計的結果相同。因此,采用偏最小二乘回歸方法仍然沒有估計出真值。

綜上,這幾種方法是目前工具誤差系數分離的主要方法,各有特點,然而都無法從根本上避免病態矩陣求逆問題,因而需要為工具誤差系數分離尋求新的解決途徑。而本文提出的方法通過引入相關系數的概念,將工具誤差系數通過因果關系重構成新的誤差模型,降低了結構矩陣的維數,并且解決了環境函數矩陣復線性的問題,避免了病態矩陣求逆的過程,可以精確求解出各系數組合值。

3 基于因果關系相關系數的辨識方法

為克服在模型不降階的前提下對參數有偏估計的不足,本文提出了一種基于因果關系的慣性制導工具誤差系數分離方法,其核心思想是在模型中各因子相關的條件下,通過對模型適當降階以求出各系數組合的精確解[8-10]。

首先,給出相關系數[8]的定義。設一組向量C1、C2、…、Cj線性相關,則存在某些非零標量ri（i=1,2, …,j-1)滿足

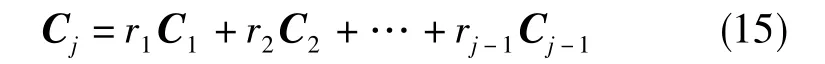
那么,對于向量 Cj與其余向量組 Ci（i=1,2,…,j-1),可以把向量組Ci看做一個n維空間的基,則其相關系數可以寫為

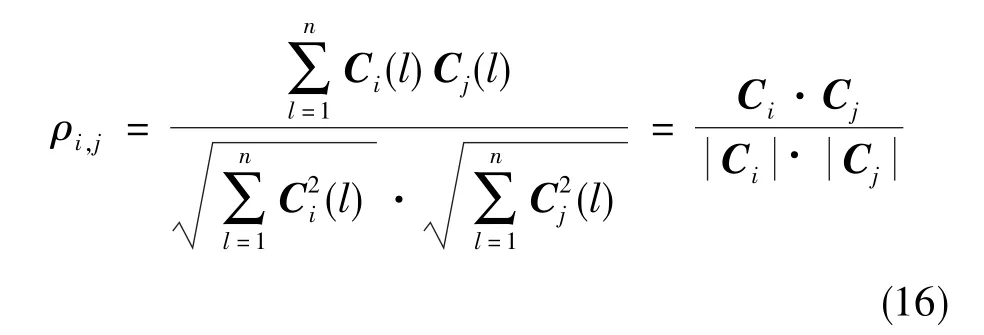
其次,將式（15)寫成基于相關系數的因果關系表達式

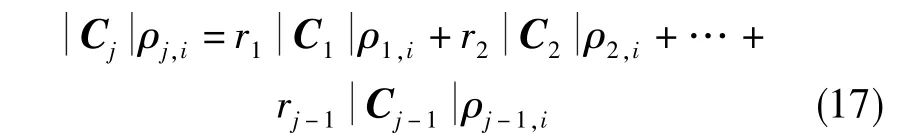
然后根據式（17),將制導系統工具誤差模型（式（1))寫成相關系數方程組

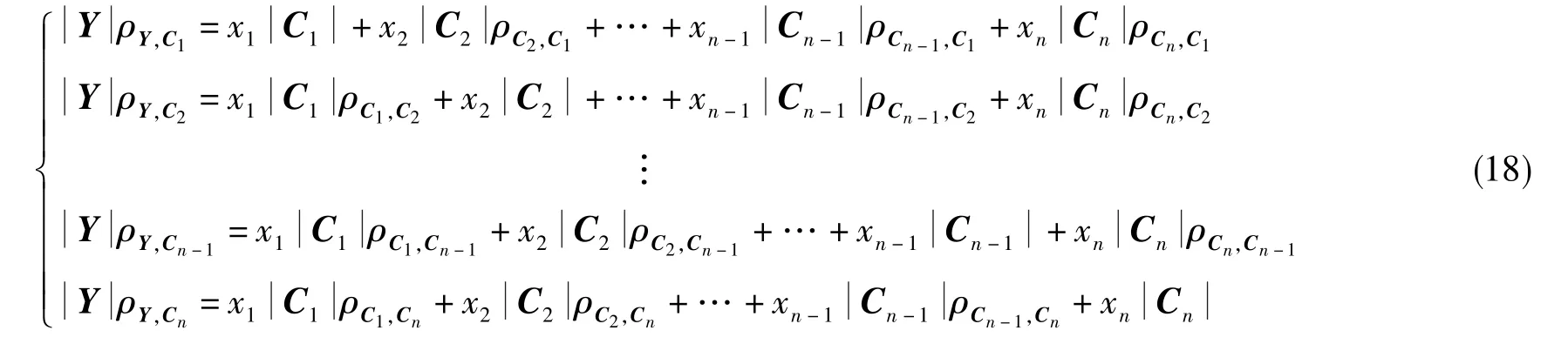
式（18)中,n=1,2,3,…,為參數的維數。

對實例采用式（18)可列寫出相關系數方程組,等效為以下矩陣方程

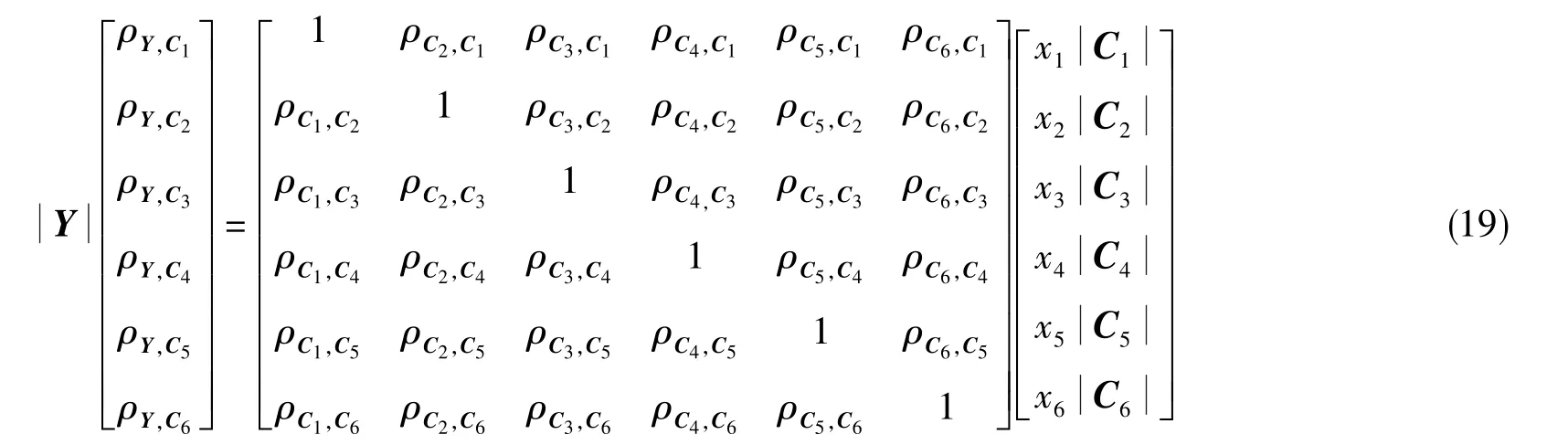
但是,采用傳統方法并不能準確求解出6個系數的真值。

因此,采用本文提出的基于因果關系的方法對實例進行求解,求解方法分為試湊法和通用法兩種。

3.1 試湊法

由于各系數的組合有多種,所以先通過嘗試的方法找到其中一種組合。

經過檢驗,由C1、C2、C3、C4組成的矩陣為奇異矩陣,令

可列寫出相關系數方程組

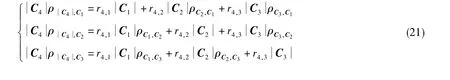
求解得到的系數為:r4,1=4,r4,2=r4,3=0。由此,有C4=4C1。

經過檢驗,由C1、C2、C3、C5組成的矩陣為奇異矩陣,令

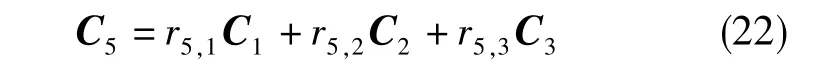
可列寫出相關系數方程組

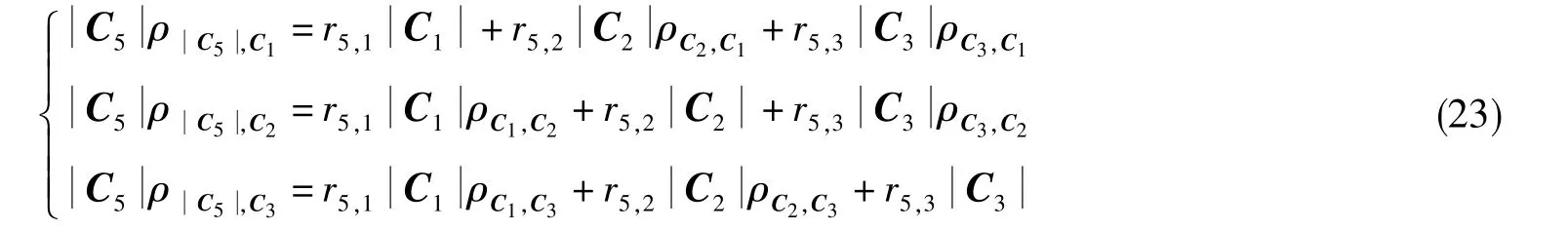
求解得到的系數為:r5,1=r5,3=1,r5,2=0。由此,有C5=C1+C3。

綜合以上結果,因果關系可以表示為圖6（a)所示。把C4和C5看作中間變量,有

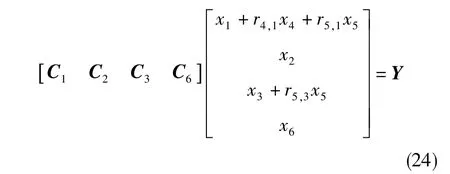
在描述因果關系時,可采用合適的化簡方式來去掉中間變量,最后的表達形式如圖6（b)所示。

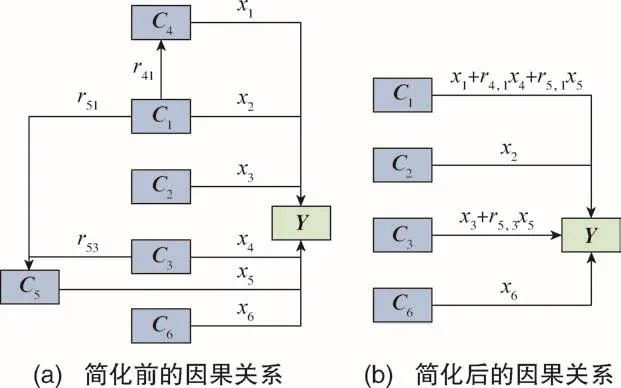
圖6 基于因果關系的簡化過程Fig.6 Simplification process based on causality

則式（19)可簡化為以下因果關系方程組

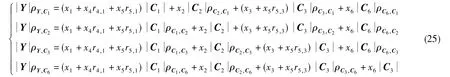
式（25)可直接求解,有

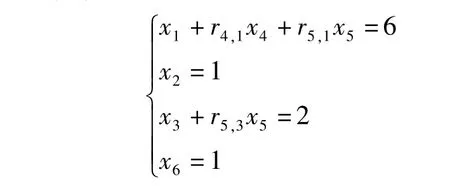
則誤差為

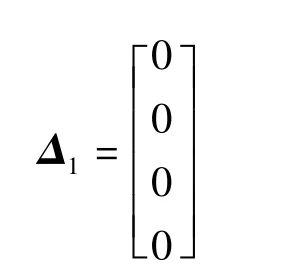
雖然通過以上求解過程最后可以得到各系數組合的精確值,但是過程比較繁瑣,不具備普適性和推廣性。下面給出一種基于因果關系的通用分析方法。

3.2 通用方法

首先,列出相關系數方程組的結構矩陣

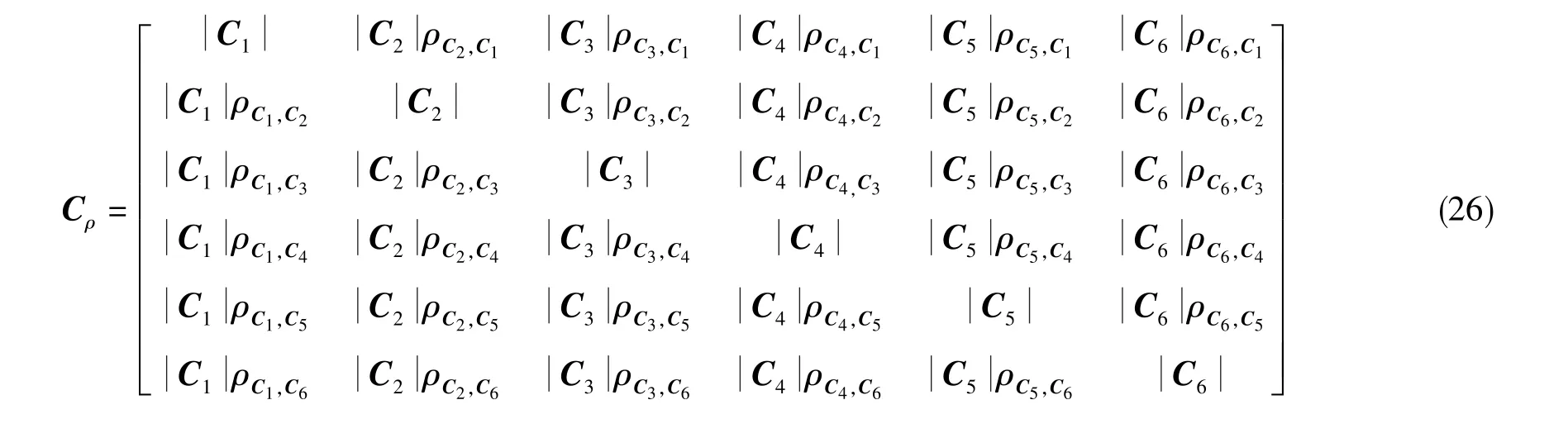
其次,求取結構矩陣的秩

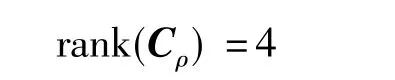
即該結構矩陣不滿秩,其基矩陣的維數為4。

然后,通過構造奇異矩陣來尋找基矩陣,若秩數和非零特征值個數相等則找到,否則繼續尋找。可以驗證,結構矩陣Cρ的第2、第3、第5、第6列可構成基矩陣,即

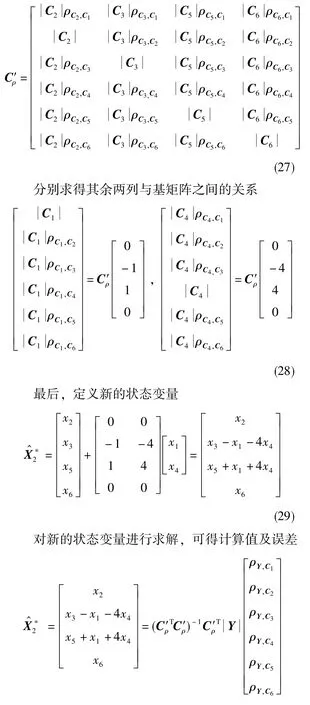
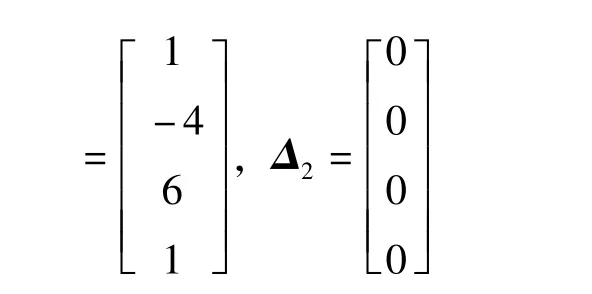
該方法通過引入相關系數的概念,將工具誤差系數通過因果關系重構成新的誤差模型,降低了結構矩陣的維數,并且解決了環境函數矩陣復線性的問題,避免了病態矩陣求逆的過程,可以精確求解出誤差系數的組合值。

4 結論

傳統的制導工具誤差分離時,環境函數矩陣各列之間存在復線性問題。為解決該問題,傳統方法有:1)基于先驗信息的Bayes估計、嶺估計,這種方法最大的缺點就是對驗前信息依賴性太強,估計結果可能會不準確;2)無需先驗信息的主成分估計、偏最小二乘估計等。這些方法的核心思想是在模型不降階的前提下估計出系數的近似解,帶來的問題就是估計有偏差。

本文提出了一種基于因果關系的慣性制導工具誤差系數分離方法,通過引入具有因果關系的相關系數,把相互之間有關聯的制導工具誤差系數進行整合,重構出新的遙外測誤差模型。整合后的新系數對應的環境函數矩陣為列滿秩,從而精確求解出誤差系數的組合值并確保了該值的唯一性,克服了主成分估計、嶺估計等傳統方法不能精確求解的缺點。把因果關系引入制導工具誤差系數分離過程中,克服了結構矩陣維數過多的問題,有利于實時在線計算制導工具誤差系數,具有簡單快捷、容易實現的優點。