樓板變形對地下大空間外墻結構設計的影響分析

柏 炯，遲 恒

[1.上海市政工程設計研究總院（集團）有限公司，上海市200092； 2.上海城市空間建筑設計有限公司，上海市200092]

0 引 言

隨著國內城市軌道交通工程的高速發展，越來越多大型多功能地下結構應運而生，諸如綜合客運站、地鐵雙線或多線換乘車站與之相連的地下空間一體化開發。而其設計方法及理論多沿用地上結構設計規范，使得對地下特殊結構形式的重要構件存在設計誤差[1]。

在工程設計中，通常將地下大空間結構近似轉化為框架- 剪力墻結構體系并根據周圍地質巖土情況施加圍壓荷載及邊界約束，并假定樓板為平面內無限剛度，即使樓板平面內各點統一位移，無平面內及平面外變形。雖然此方法極大簡化了計算模型，提高了設計效率。但實踐證明對于深埋地下大空間結構不宜采取此假設，需要還原樓板真實平面內外剛度。尤其對于局部抗側力構件與樓板平面內剛度比過大，如樓板開洞，板墻厚度比、整體結構的長寬比較大及抗側力構件間距較大等情況下，若不考慮樓板變形，即按照剛性樓板計算，計算配筋誤差較大。因此，本文基于日照綜合客運站北廣場地下空間建筑工程項目對地下室外墻進行計算分析，探討地下空間外墻結構內力隨板墻剛度比變化的分布規律及樓板變形對結構協同作用的影響[2]。

1 計算模型的建立

1.1 通用地下室外墻設計方法

在構造上地下結構外墻底部將與剛度較大的基礎底板或基礎梁相連，且底板普遍外伸，即底部兩側的剛度之和遠大于墻體剛度，故外墻底邊界設定為嵌固。若地下結構外墻未延伸至地面以上時，外墻與地下結構頂板相接，頂板剛度略小于墻剛度，故外墻頂邊界可設定為鉸接。而外墻與中間層樓板相連存在一定的約束效應，即實際邊界情況類似于半剛性支座。但設計上通常認為相比外墻強剛度其約束力可忽略，僅考慮水平向位移約束，即近似于將板墻邊界按水平鉸接考慮[3]。

當地下結構中無橫墻布置或橫墻間距大于本層高的2 倍時，左右支座約束作用很小可忽略，地下室外墻可按“上鉸下固”板或連續梁計算，見圖1。

圖1 地下空間結構外墻計算模型

內力計算時，地下室外墻壁板依據兩個方向跨度比值可分為雙向受力（0.5≤Ly/Lx≤1）和單向受力（Ly/Lx＜0.5）兩種情況。雙向受力時，外墻壁板在三角形荷載和均布荷載作用下的計算公式詳見《建筑結構靜力計算手冊》，考慮到鋼筋混凝土板的各向異性，則其彎矩計算公式為[4]：

其中本工程外墻多為單向受力，其在水土梯形荷載作用下的墻彎矩計算公式為：支座彎矩為式（3）；跨中最大彎矩為式（4）。

其中最大彎矩作用點位于x=0.427 4l0處（q2＞q1）。

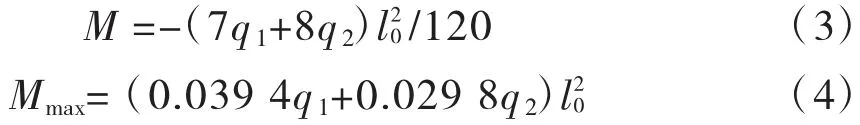
式中：q1、q2分別為外墻頂板、底板位置的側向壓力[4]。

1.2 地下室外墻有限元計算方法

依據《全國民用建筑工程設計技術措施》中樓（屋）蓋結構設計與構造標準，當樓板在自身平面內相對撓度小于或等于1/12 000 時，可認為樓板在其自身平面內為剛性板，則可依據上述計算模型及公式進行內力分析。而對于深埋地下結構在承擔較大的側向水土壓力時，樓板剛度有限，結構協同作用及平面內整體性能介于柔性樓板和剛性樓板之間，可稱為半剛性樓板，且靠近外墻的邊跨區的低層樓板不僅存在平面外彎曲變形且存在平面內壓縮及剪切變形，須用彈性板構建板墻模型計算其內力。

為分析真實工況下地下結構中樓板內力及變形位移分布，得到各項內力值的精確解，本文采用有限元法將連續介質離散化為有限單元組合體進行分析，表達式如下。其中，總剛度矩陣由各單元剛度組成。

式中：[K]為總結點位移矩陣；｛α｝為總結點力矩陣；｛P｝為總剛度矩陣。

在計算實際工程中，使用Midas、Robot 軟件中四節點殼單元模擬外墻及樓板，還原平面內外真實剛度，并結合兩節點梁單元模擬鋼筋混凝土的框架梁柱。與SATWE 計算模型對比，可知采用彈性樓板計算相比剛性樓板時結構的側向剛度偏小、結構偏柔、自振周期增大；樓板變形使結構的側移和層間位移角比剛性樓板大。其改進的計算簡圖，見圖2。中板對側墻的平面支撐由鉸接該為彈簧支座，彈性系數需要通過加載試驗迭代計算獲得。考慮到整體變形協調，外墻在支座位置處的彎曲位移與樓板壓彎變形數值接近[5]。

圖2 地下結構外墻彈性樓板計算簡圖

2 工程概況

本文基于日照綜合客運站北廣場地下空間建筑工程討論樓板剛度對地下大空間外墻配筋設計的影響。該工程站前廣場主體結構為地下三層，埋深約17 m。平面寬度約199 m，平面長度約445 m（最長位置）。采用十字梁板樓蓋方案，典型柱網尺寸為8.4 m×8.4 m。地下一層層高5.5m，地下二層層高5.5 m，地下三層層高4.2 m，頂板板厚250 mm，B1、B2 層板厚150 mm。地下室頂板覆土厚2.5 m 左右。設定地下水位標高為設計地面標高。本工程主要結構構件混凝土強度等級為C35，受力鋼筋主要采用HRB400 級。采用Midas Gen 構建整個工程計算模型[6]，見圖3。

圖3 日照北廣場客運站整體模型

3 設計分析

在地下室外墻設計時，一般僅考慮水平圍壓作用下結構受力情況。按連續梁計算外墻豎向彎矩，見圖4；由Midas 整體建模計算側向水土壓力標準組合下地下結構外墻彎矩，見圖5。

圖4 采用連續梁計算外墻豎向彎矩圖

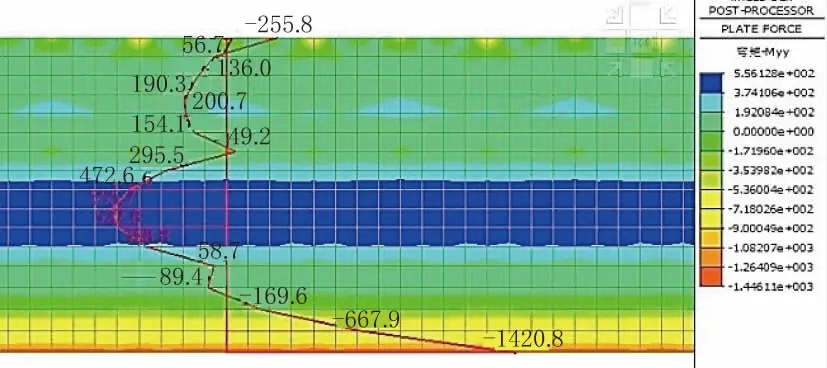
圖5 采用Mida s 整體模型計算外墻豎向彎矩圖

由計算結果可推斷：隨著樓板厚度越小，樓面平面內剛度越低，與外墻剛度比降低，有限元模型結果與連續梁模型內力分布相差較大，其中墻支座負彎矩值遠低于傳統計算結果，跨中正彎矩提升近2 倍；且隨著土層深度增加，由外墻傳遞于樓板上的圍壓增大，樓板同時存在平面內剪切及壓縮變形和平面外彎曲變形，見圖6、圖7。因此，樓板變形過大以致無法提供足夠的側向支撐力，則有限元計算得到的內力分布與無限樓板支座的連續梁模型結果誤差較大。配筋時需要考慮內力重分布進行包絡設計。

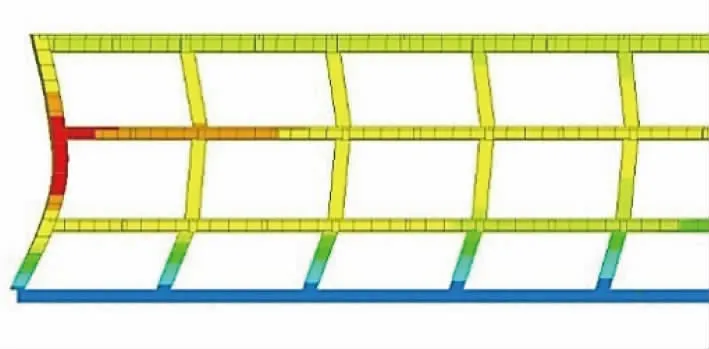
圖6 采用Mida s 整體模型計算外墻側向變形

圖7 側向水土壓力標準組合地下-1F、-2F 樓板變形

地下結構外墻主要以彎曲變形為主，即抗側剛度可近似由抗彎剛度EwIw表示。式中：Iw為結構每延米的外墻慣性矩。低層邊跨樓板主要以壓縮變形為主，即抗側剛度為EfAf。地下結構外墻兩個方向的跨中內力最大值皆隨板墻剛度比減小而增大，見圖8，其中豎向彎矩呈3 次冪函數增長。且需要校核水平向構造配筋，可提高鋼筋等級、減小間距，或設置暗梁、暗柱。

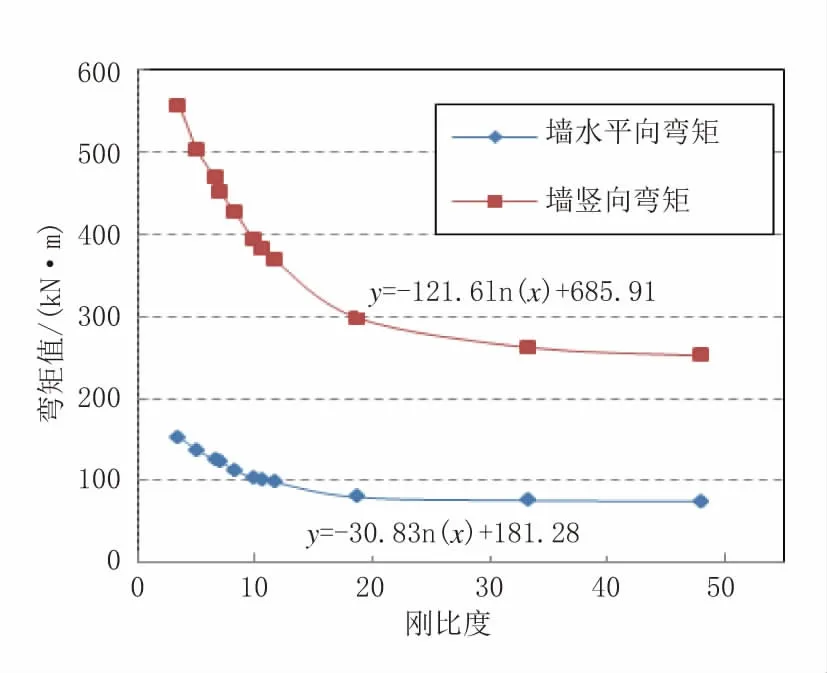
圖8 外墻最大彎矩隨剛度比的變化規律

分別依據剛性板及彈性板模型進行外墻內力計算，可得彎矩在樓層跨中處誤差值隨剛度比的變化規律，見圖9。初始模型板厚150 mm，墻厚800 mm。隨著墻板厚度接近，板墻剛度比逐漸增大，墻跨中彎矩誤差值降低，且在板墻厚度相同時誤差值趨于0。在樓板支座外墻彎矩處誤差值隨剛度比的變化規律，見圖10。隨著板墻剛度比增大，彎矩誤差值降低，其中中板B1 層誤差值以冪指數曲線降低。而B2 層隨墻板剛度增加其誤差值趨于40%，即平面內無限剛假定不適用于多層地下結構的低層墻體計算模型。探究墻內力誤差值隨深度的變化，將原模型由三跨改為兩跨及四跨，計算中板支座處彎矩誤差值，見圖11。隨樓層降低誤差值增大，同一標高處結構層數越多誤差值越大[7]。

圖9 樓層跨中處外墻彎矩差值隨剛度比的變化規律

圖10 樓板支座處外墻彎矩誤差值隨剛度比的變化規律

圖11 不同標高處墻內力誤差值

由于本工程板墻剛度比相差較大，若不改變墻板厚度時需要依據以上分析規律優化設計方案。依據《建筑結構荷載規范》（GB 50009—2012）對作用在地下結構外墻的荷載進行組合計算，其中地面超載取為20 kN/m3。對外墻進行包絡設計，見表1。

表1 配筋計算

因此，在原配筋圖的基礎上，依據有限元模型計算結果，對墻內側樓板支座處附加受拉鋼筋，可適當減少墻外側低層板支座處附加鋼筋長度，見圖12。鄰近外墻樓板還需要驗算在水土壓力和豎向荷載組合下是否滿足撓度和裂縫要求，避免進入塑形階段前裂縫大于規范要求，影響結構的耐久性和安全性。對于板墻剛度比小、低層樓板要依據其內力值對邊跨板進行板厚調整，除局部加厚還可采取其他結構構造措施。例如增設暗梁形成三角形穩定結構[9]。

圖12 優化后墻體配筋圖

4 結 論

本文通過調節結構墻板厚度、樓的剛度比來探討地下大空間結構外墻的內力分布規律。由此得出結論：隨著板墻剛度比降低，地下結構中板剛度相比于頂、底板平面內剛度有明顯降低，則其對側墻的支撐作用明顯減弱。從而使側墻在各樓層跨中處正彎矩隨著剛度比降低而顯著增加，且其極值點位置隨著層數的增加而下移。綜上，在進行地下大空間結構內力分析時應充分考慮結構的空間效應，避免平面簡化模型對各結構構件協同受力作用和樓板開洞等特殊情況的忽略，合理調配板墻的剛度比，使傳統計算結構更真實反映地下外墻在水土圍壓及地震作用下的受力情況。并依據設計規范及地下結構外墻真實內力分布增置受力鋼筋及防裂構造筋。實現地下結構設計的合理性及整體結構的安全性，也可避免結構保護設計時的工程資源浪費現象。