基于模態試驗和沖擊響應試驗的模型動力學參數修正

彭揚林，石 蒙，劉洪英，董 睿，韓 旭，趙亞雄，劉 磊，宮曉清

（中國航天員科研訓練中心，北京 100094）

0 引言

航天產品的研制過程中，常用沖擊響應譜動力學試驗模擬航天發射過程的沖擊動力學環境。而沖擊響應數值仿真模擬可以輔助提升試驗的驗證效率，降低試驗成本，指導沖擊設備研發和試驗調試。有研究人員對沖擊響應譜的計算實施、不同參數下沖擊響應譜計算值的變化規律等進行了研究，但是大多缺乏試驗數據對比，無法評估仿真計算的準確性；又有研究人員針對試驗驗證和模型修正做了大量工作，但是對于阻尼修正的指導作用有限。沖擊響應是一個復雜振蕩的過程，要對其進行準確的數值模擬，需要對模型的動力學參數進行修正。

當前，針對沖擊響應譜試驗過程的動力學參數修正的研究相對較少。本文擬基于模態試驗和沖擊響應試驗過程，對數值計算模型動力學參數進行修正，模態試驗過程修正彈性模量、泊松比和厚度參數，沖擊響應試驗過程修正阻尼參數，旨在提高沖擊響應譜預測精度。

1 模態試驗及參數修正

1.1 模態試驗實施

模態試驗采用東方振動和噪聲技術研究所的INV3062T 型信號采集分析儀，結合力錘和力傳感器實施。被測的響應板為500 mm×400 mm×10 mm的鋁合金平板，其四角通過螺栓安裝固定。模態試驗過程采用多點激勵單點響應的方式，根據平板尺寸按照100 mm 的間隔設置激勵點，激勵點編號按從左至右、從下至上的順序編為1～30，原點導納（響應傳感器）位于激勵點16，如圖1 所示。試驗時，分別對激勵點1～30 進行敲擊，采集各點的激勵力和加速度響應信號，得到響應板的各階模態固有頻率。

圖1 模態試驗響應板上的激勵點及其編號Fig. 1 Excitation points and their numbers on the response plate of modal test

1.2 模態參數修正

建立響應板的有限元模型如圖2 所示，對其四角的螺栓安裝孔進行固定約束，然后計算結構的固有頻率，響應板的材料參數為彈性模量71 GPa、泊松比0.33。

圖2 響應板的有限元模型Fig. 2 Finite element model of the response plate

以試驗測試得到的固有頻率（見表1）為優化目標，以響應板的彈性模量、泊松比和厚度為優化參數，基于響應面優化的方法進行優化計算。

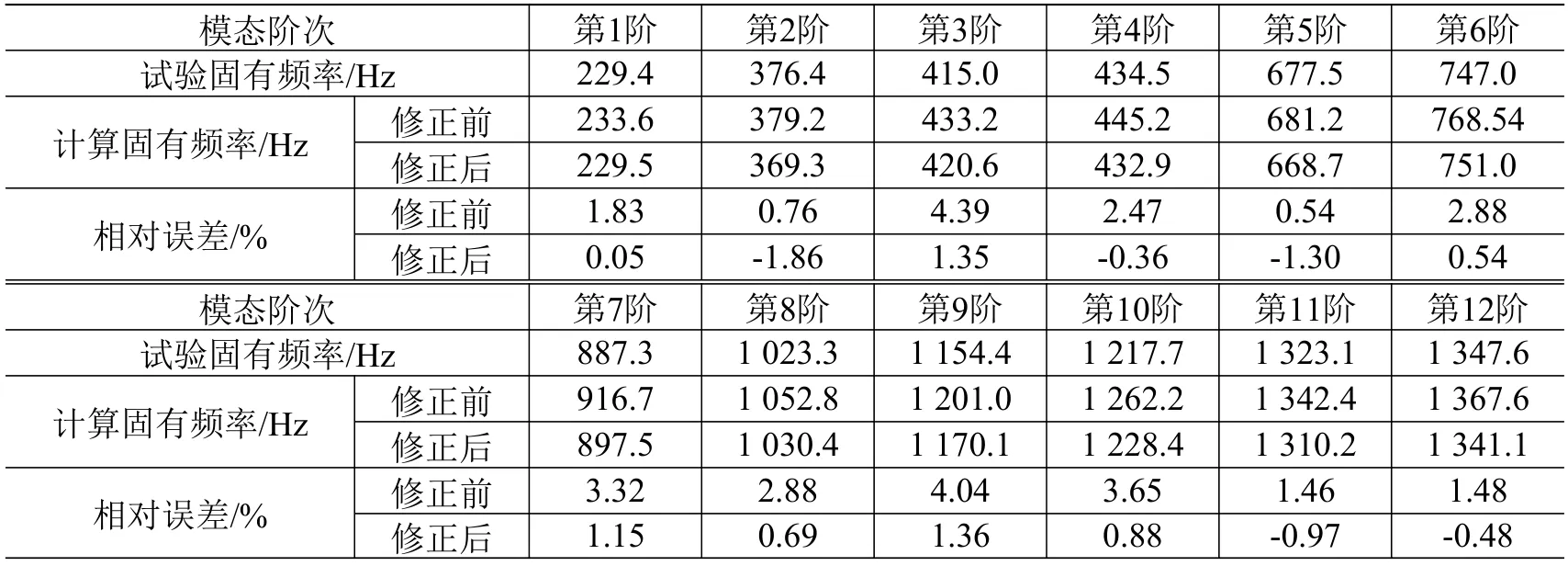
表1 參數修正前/后的響應板固有頻率Table 1 Natural frequency of response plate before and after parameter modification

多項式型響應面是常用的響應面類型，對于二次多項式響應面，可表示為

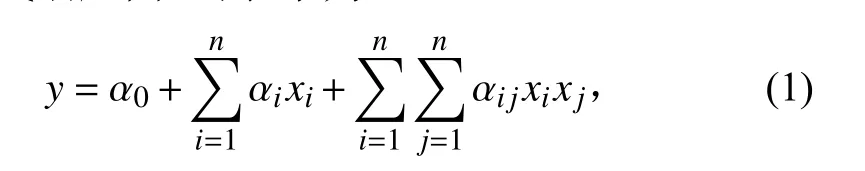
式中：為響應面；為輸入變量；、α、α為回歸系數。由于采樣點數量通常大于多項式的項數，所以式(1)為超定方程，無法得到精確解，常用最小二乘法擬合求得其近似解。得到的最優參數為：彈性模量66.927 GPa，泊松比0.3625，厚度9.9956 mm。

參數修正前/后的響應板前12 階模態固有頻率值如表1 所示。經過參數修正后，前12 階模態固有頻率計算值的相對誤差大部分較修正前有所降低，均在±2%內，說明基于模態測試的動力學參數修正有效。后續沖擊響應譜數值仿真過程，采用修正后的彈性模量、泊松比和厚度值進行計算。

2 沖擊響應譜試驗及參數修正

2.1 沖擊響應譜試驗實施

響應板及沖擊響應的測量點位置如圖3 所示。沖頭提高到設定高度后，經過自由落體過程與響應板發生碰撞，通過加速度傳感器采集響應點的時域數據并根據Runge-Kutta 算法，在品質因子=10、分析頻率間隔為(1/6)oct 條件下，進行沖擊響應譜的計算。

圖3 沖擊響應測試的測量點位置Fig. 3 Positions of measuring points on the response plate for shock response test

沖擊高度為6.3 cm 的條件下，響應點1 和點2 的沖擊時域曲線和響應譜曲線如圖4 和圖5 所示。

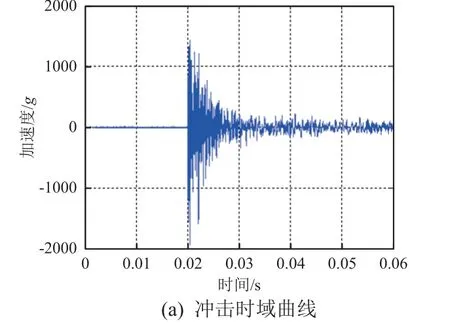
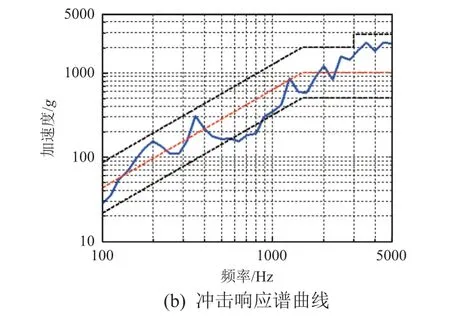
圖4 響應點1 的沖擊響應曲線Fig. 4 Shock response curve at point 1

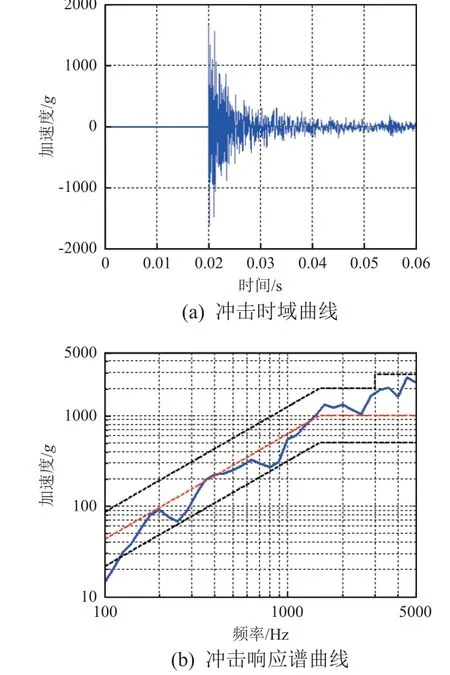
圖5 響應點2 的沖擊響應曲線Fig. 5 Shock response curve at point 2

2.2 沖擊響應譜數值仿真

以圖2 所示的有限元模型進行數值仿真，響應板上的4 個安裝點固定約束，沖頭賦予按沖擊高度換算的自由落體速度；沖頭和響應板發生碰撞沖擊，提取傳感器響應測量點的加速度時域響應數據，采用與2.1 節沖擊響應譜試驗相同的計算參數，得到沖擊響應的數值計算結果。

數值計算的阻尼采用Rayleigh 阻尼，通過質量阻尼系數和剛度阻尼系數來模擬沖擊響應過程的振動衰減。為了評估數值計算和沖擊試驗過程的響應差異程度，計算在頻率間隔為(1/6)oct 條件下，數值計算和試驗過程的沖擊響應譜曲線各分析頻率點的均方根誤差

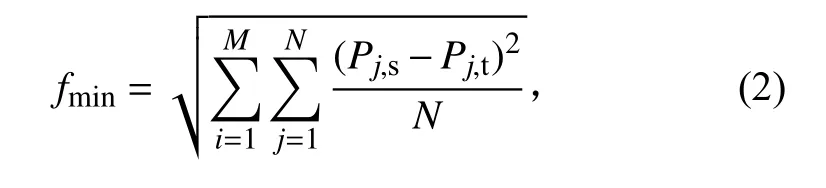
式中：為評價使用的響應點序號，為響應點數量，本文=2；為分析頻率點的序號，為分析點數量，本文=35；P和P分別為數值計算沖擊響應譜曲線和試驗沖擊響應譜曲線上第個分析點的加速度值。評價目標越小，則認為數值計算得到的響應和試驗響應間的差異越小。

2.3 阻尼系數修正

Rayleigh 阻尼和各階模態阻尼比的關系可以表示為

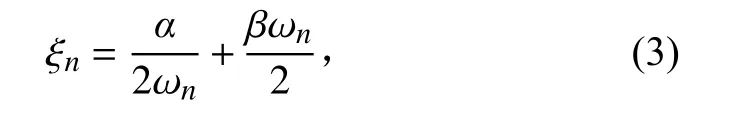
式中：ξ為第階模態阻尼比；為質量阻尼系數；為剛度阻尼系數；ω為第階模態的固有頻率。該沖擊響應譜的計算頻率范圍為100～5000 Hz，在該范圍內結構的最小和最大固有頻率分別為229 Hz和4987 Hz。假設各階模態的阻尼比均為0.03 時，代入式(3)可以計算得到：=82.7，=1.83×10。

為了找到最優的阻尼系數，對如表2 所示的參數進行全因子實驗的數值仿真計算，并與圖4 和圖5 的試驗沖擊響應譜曲線對比進行均方根誤差計算。得到質量阻尼系數、剛度阻尼系數和均方根誤差值的關系如圖6 所示的標記點。對所有標記點進行曲面擬合，得到曲面上最低點的質量阻尼系數、剛度阻尼系數和均方根誤差值分別為113.88、1.75×10和438.01。

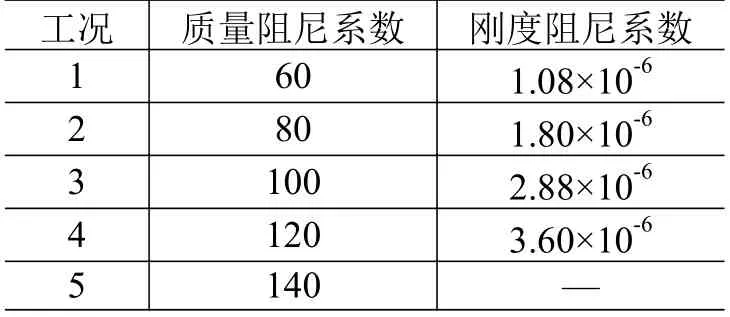
表2 全因子實驗參數Table 2 Parameters of the full factorial experiment

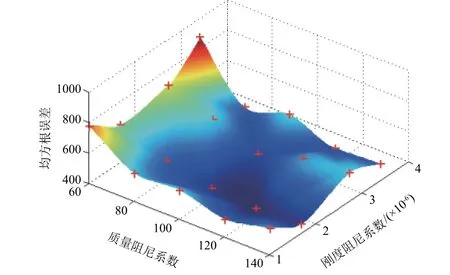
圖6 阻尼系數和均方根誤差的關系Fig. 6 Relationship between damping coefficients and root mean square error

3 試驗驗證

在基于模態試驗修正的彈性模量、泊松比和厚度值，以及基于沖擊響應試驗修正的質量阻尼系數、剛度阻尼系數條件下，對沖擊高度為3.3 cm、9.3 cm、12.3 cm 的沖擊工況進行驗證。相關工況的參數見表3。

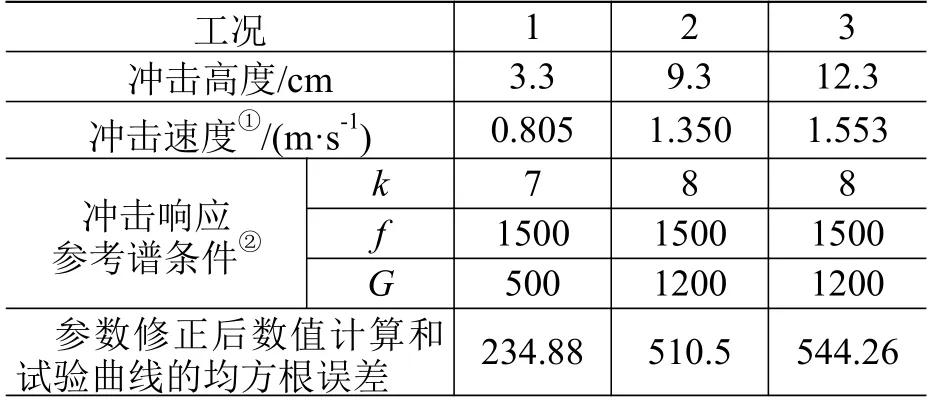
表3 試驗驗證的不同工況Table 3 Different working conditions in verification test

3 個工況對應的修正前/后數值計算以及沖擊試驗2 個響應點的響應曲線對比如圖7～圖9 所示。可以看到，響應板上2 個響應點的修正后數值計算曲線與試驗響應曲線均吻合較好，大部分頻率段的誤差在±6 dB 以內，較修正前的數值計算結果誤差明顯減小。這說明通過動力學參數修正，數值計算模型能夠較好地模擬該響應板的沖擊響應。

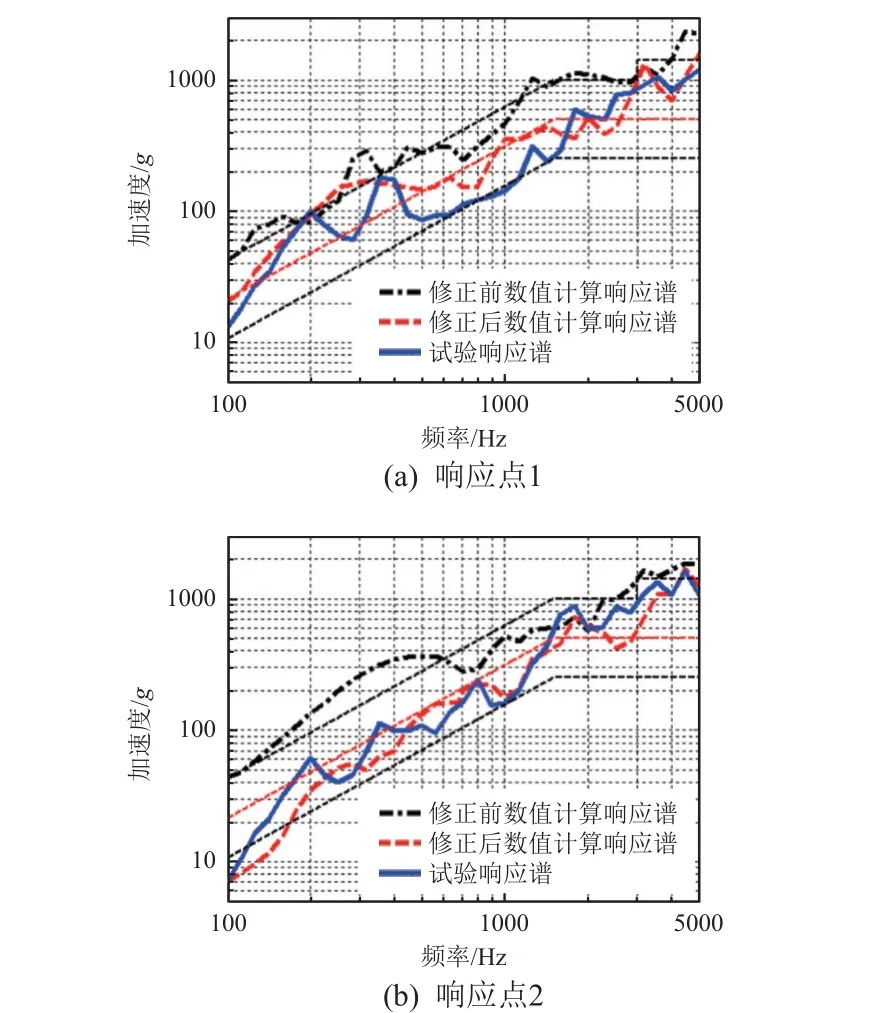
圖7 工況1 的計算及試驗沖擊響應譜Fig. 7 Calculated and tested shock response spectrums under working condition 1

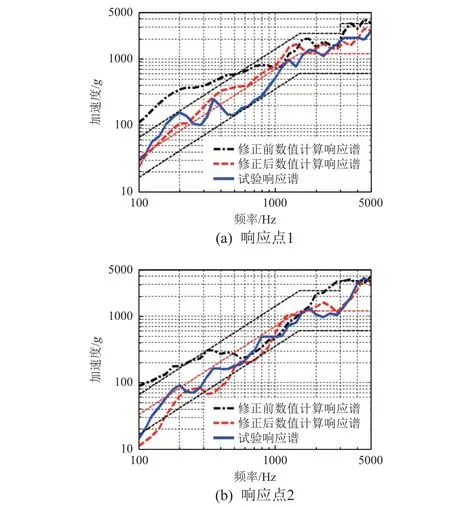
圖8 工況2 的計算及試驗沖擊響應譜Fig. 8 Calculated and tested shock response spectrums under working condition 2

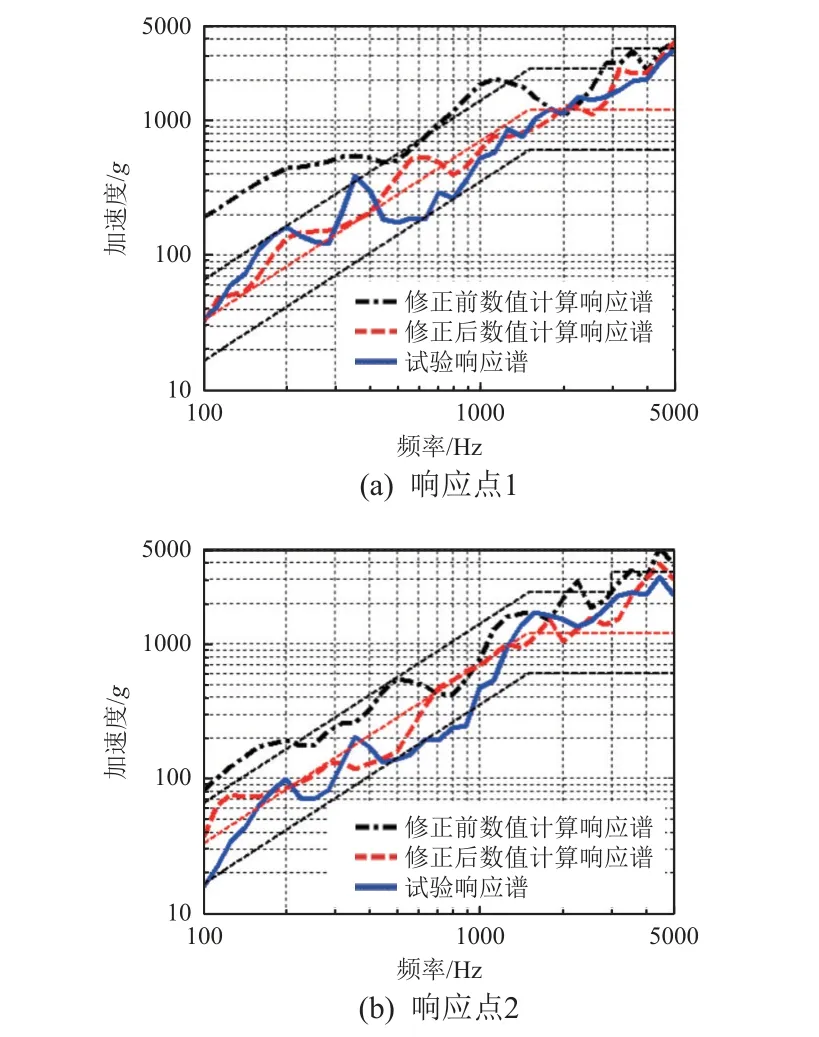
圖9 工況3 的計算及試驗沖擊響應譜Fig. 9 Calculated and tested shock response spectrums under working condition 3

4 結束語

分別通過模態試驗和沖擊響應試驗對響應板結構的模型動力學參數進行修正。修正后，結構的固有頻率誤差在±2%以內；模型在預測沖擊高度為3.3 cm、9.3 cm、12.3 cm 工況下的沖擊響應過程中取得較好的預示效果，大部分頻率段的誤差在±6 dB 以內。可見，動力學參數修正后的數值計算模型有效提高了預測精度，對于實際工程中的設備研制以及沖擊響應譜試驗規范調試具有一定的指導作用。