濕熱定型機溫濕度解耦控制系統

趙世海，李 果

（1.天津工業大學 機械工程學院，天津 300387；2.天津工業大學天津市現代機電裝備技術重點實驗室，天津 300387）

織物在生產過程中由于受到機械、化學等作用產生形變，并不能直接用于染色、印花等后續工序的加工。熱定型可以消除在生產過程中產生的強迫高強變形，并同時釋放纖維的內部應力[1]。熱定型后的織物在尺寸穩定性和機械性能方面均得到顯著提高，還能使織物表面起球、表面平整性等性能得到改善。

與干熱定型相比，濕熱定型后的織物手感豐滿、柔軟[2]。但是傳統的溫濕度控制系統將溫度和濕度作為2個相互獨立的系統進行調節，忽略了兩者之間的耦合聯系，從而使系統的控制質量下降。李旻[3]將模糊理論運用到溫度控制，證明該方法穩定可靠；譚寶成等[4]將模糊PID運用到熱定型機溫度控制中，降低了在控制過程中的遲滯和超調現象。但上述方法均未考慮到在實際應用中來自其他系統的耦合、干擾。

針對濕熱定型機這種具有強耦合、大遲滯的溫濕度控制系統，本文提出一種基于模糊控制的前饋解耦控制方案。先利用階躍響應法找到傳遞函數，并根據傳遞函數設計出解耦系統，再將模糊控制融入到設計好的解耦系統當中，以達到解耦目的，同時降低在控制過程中的遲滯現象[5]。

1 熱定型機溫濕度系統建模

熱定型機由進布架、操控臺、針鋏鏈、燃燒室、烘房、落布架幾個部分構成。布料首先放入進布架上，由輥軸輸送到針鋏鏈上，被拉幅之后送進烘房，烘房內部結構如圖1所示。烘房內對溫度調節過程如下：空氣在燃燒室被加熱后，熱風經由鼓風機吹風口吹向胚布，最后與烘房的熱蒸汽混合。顯然當烘房溫度增加時，濕度會隨著溫度提升而降低；當對濕度進行調節時，飽和水蒸氣會通過輥軸內的加濕設備進入烘房內部，溫度也會隨濕度的增加而降低，即在熱定型機內部溫、濕度存在較強的耦合關系。為了解除存在于溫度、濕度之間的耦合效應，建立烘房內部的合理的數學模型至關重要。

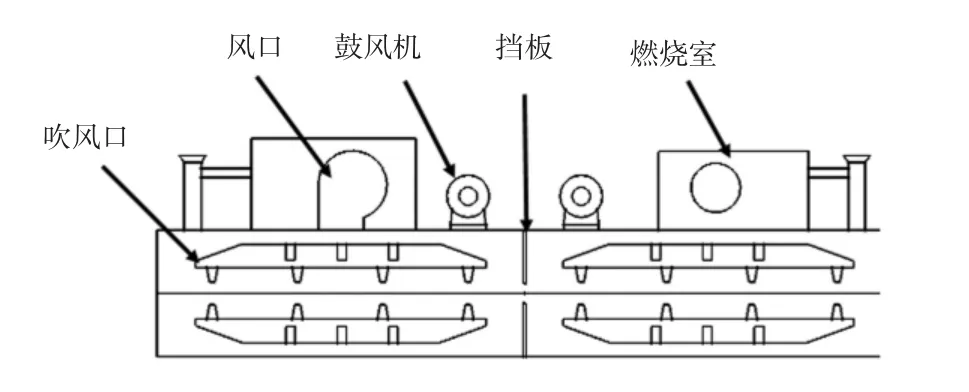
圖1 烘房結構示意圖Fig.1 Schematic diagram of drying room structure

溫濕度系統具有強耦合和非線性特性，烘房內的溫度受風道出風口溫度、烘房內部體積、初始溫度等一些因素影響，在不考慮外界干擾下，根據能量守恒定律[6]：

式中：ρ為空氣密度；CP為空氣定壓比熱容；V為烘房內部體積；f為空氣流量；Ts為出風口溫度；Th為回風口溫度。

將模型兩邊進行拉式變換，得到烘房內溫度控制系統為一階傳遞函數[7]：

溫度控制系統為非線性、大遲滯控制系統，考慮滯后環節影響，串聯滯后環節后得到G1（s），傳遞函數為：

式中：K1為溫度控制系統的增益系數；τ、T分別為溫度控制系統的遲滯時間和時間常數；s為復變量。

使用階躍響應法[8]確定加熱器-溫度的數學模型。實驗時箱內溫度為50℃，關閉濕度控制器的同時給溫度控制器一個擾動信號，記錄溫度的變化曲線直至穩定，階躍響應曲線如圖2所示。

圖2 加熱器-溫度階躍響應圖Fig.2 Diagram of heater-temperature step response

由圖2可以得到：

式中：K為比例增量；Y（∞）為系統穩定后溫度；Y（t0）為初始溫度；Δu=0.5為加熱功率干擾量。y*（t）為y（t）的無綱量，y*（t）與公式（3）中的時間常數T、純遲滯τ滿足如下關系[9]，選取2個不同坐標下t1、t2建立如下方程組：

在圖2中，當y*（t1）=0.39時，t1=280 s，y（t1）=51.04；y*（t2）=0.63時，t2=460 s，y（t2）=51.6。將參數帶入式（5）解得T=360，τ=100，。將求解結果帶入式（3）既得出加熱器-溫度系統G11的數學模型為：

使用上述方法可求得G12、G21、G22的數學模型為：

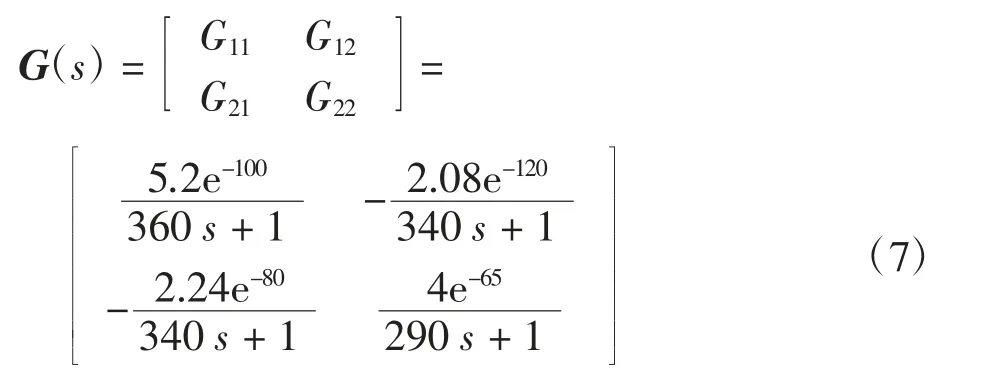
式中：G11為加熱器對溫度傳遞函數；G21為加熱器對濕度傳遞函數；G12為加濕器對溫度傳遞函數；G22為加濕器對濕度傳遞函數。

2 前饋補償解耦方案

當產品在烘房進行加工時，溫度和濕度都是影響產品質量的重要因素。但在烘房內部，溫、濕度并不是獨立的變量[10]，單一地調節某一方，都會引起另一方的變化。溫度、濕度之間的耦合關系如圖3所示。

圖3 溫度濕度耦合關系圖Fig.3 Coupling diagram of temperature and humidity

由溫濕度耦合關系得出熱定型機控制與輸出之間的傳遞矩陣：

式中：Yt、Yh為烘房內部的溫度和濕度；Ut為溫度控制器輸出；Uh為濕度控制器輸出。溫度和濕度的輸出結果均被Ut、Uh共同控制[11]。

針對溫濕度系統耦合控制不理想的問題，采取前饋解耦的方式。前饋解耦是根據控制不變性原理來設計解耦控制器的，以矯正方式使溫度和濕度在調整過程中穩定在設定值，達到解耦目的[12]。解耦控制原理如圖4所示。

圖4 溫度濕度解耦控制原理圖Fig.4 Schematic diagram of temperature and humidity decoupling control

式中：Tset為設定溫度；RHset為設定濕度；Ut為溫度控制器輸出；Uh為濕度控制器輸出；F21為溫度-濕度解耦傳遞函數；F12為濕度-溫度解耦傳遞函數；

在工作過程中濕度的增加會影響溫度的變化，反之亦然。通過測量干擾的大小和方向[13]，增加前饋補償模型以抵消干擾對被控量的影響。F12、F21為前饋補償信號，傳遞矩陣為：

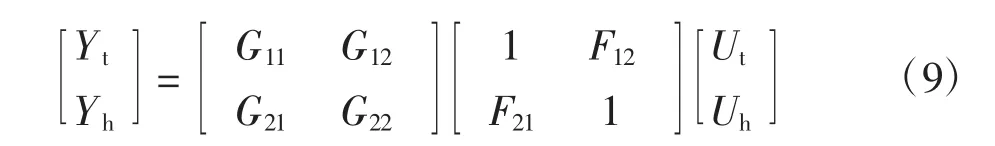
在解除耦合后，溫度、濕度不再相互影響。此時可將式（9）傳遞模型看作對角矩陣，當控制矩陣變為對角矩陣后，Yt僅被Ut控制，Yh也僅被Uh控制，輸入輸出關系可由式（10）來表示：

將式（10）代入式（9）中求出解耦傳遞函數F21、F12和等效傳遞函數中的W11、W22：

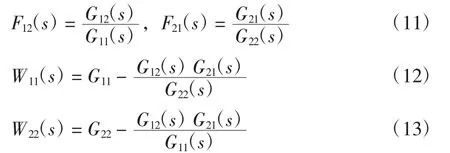
在文中設計的溫濕度控制解耦環節中，圖4控制器C1（s）、C2（s）采用模糊控制的方式，可有效降低控制過程中的遲滯[14]。在加入補償矯正后，溫度、濕度控制系統的耦合效應消除，經過解耦后的控制系統等效圖如圖5所示。

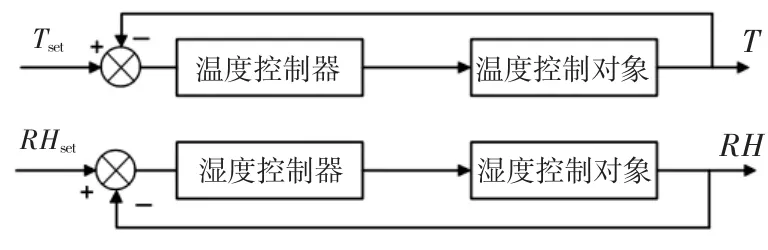
圖5 溫濕度解耦等效圖Fig.5 Equivalent diagram of temperature and humidity decoupling

3 模糊控制模塊設計

PID控制具有結構簡單、工作可靠、易于調整等優點，被廣泛運用在工業生產中。但當系統中含有復雜變量或者沒有具體數學模型時，傳統的PID控制很難獲得理想的控制效果[15]。模糊PID控制器會將實際值與期望值的偏差和偏差變化率2個參數輸入到模糊控制器中[16]，在經過模糊化、模糊推理和解模糊過程后得到ΔKP、ΔKI和ΔKD3個修正參數，并將3個參數輸送給PID控制器得到新的KP、KI、KD。模糊PID控制器充分利用了人工調節實踐經驗，在控制過程中對PID參數進行調整，與傳統PID控制相比反應更加迅速，在遇到干擾時擁有更好的魯棒性[17]。模糊控制器結構如圖6所示。模糊控制器設計過程主要包括：輸入量e、ec模糊化；模糊推理；反模糊化。

圖6 模糊PID系統結構Fig.6 Structure of fuzzy PID system

3.1 e、ec模糊化

模糊化是將輸入量e、ec由精確值變為模糊語言變量值的過程。將模糊語言變量子集劃分為“NB”（負大）、“NM”（負中）、“NS”（負小）、“ZO”（零）、“PS”（正小）、“PM”（正中）、“PB”（正大）7個變量等級。根據隸屬度函數確定隸屬度[18]，隸屬度函數這里采用高斯隸屬函數，如圖7所示。

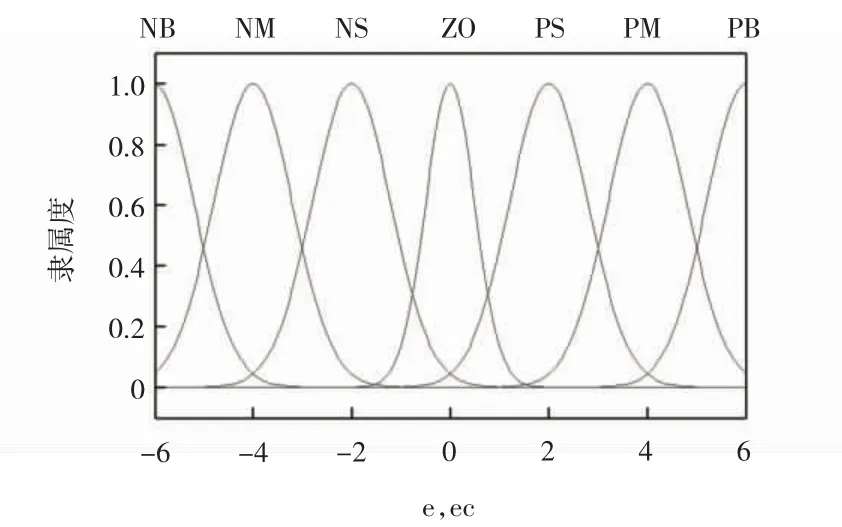
圖7 輸入變量的隸屬度函數Fig.7 Membership function of input variables

3.2 模糊推理

決策推理是模糊控制的核心，輸入量依據模糊規則得到相應輸出變量ΔKP、ΔKI和ΔKD。按照熱定型機管控人員的日常經驗，歸納整理成模糊規則庫，使用if A and B then C語句進行模糊規則的設計[19]。每1個輸入量均含有7個語言變量值，因此，模糊規則的個數共為49個。

3.3 反模糊化

反模糊化是指將3個輸出變量由模糊語言變為3個具體的數值[20]，去對應PID控制器的3個參數ΔKP、ΔKI和ΔKD。輸出變量的語言變量值為“NB”（負大）、“NM”（負中）、“NS”（負小）、“ZO”（零）、“PS”（正小）、“PM”（正中）、“PB”（正大），隸屬度函數同樣為高斯函數，如圖8所示。

圖8 輸出變量的隸屬度函數Fig.8 Membership function of output variables

4 仿真實驗

傳統的溫、濕度控制系統實際將溫度、濕度看作2個相互獨立無關聯的控制變量，但在實際控制過程中溫、濕度耦合作用明顯。在加入模糊和解耦模塊后以Matlab作為仿真平臺，分別對耦合系統以及解耦的系統進行仿真模擬，對解耦效果進行驗證。

4.1 溫、濕度控制效果仿真

設置烘房溫度初值為20℃，相對空氣濕度為30%，濕熱定型穩態下工作溫度為130℃，當采用飽和蒸汽時效果與水浴法接近，定型效果較差，本文采用工作時相對濕度為80%。溫、濕度2個參數的采樣周期均設置為10 s一次，仿真時間為3 500 s。仿真結果如圖9、圖10所示。

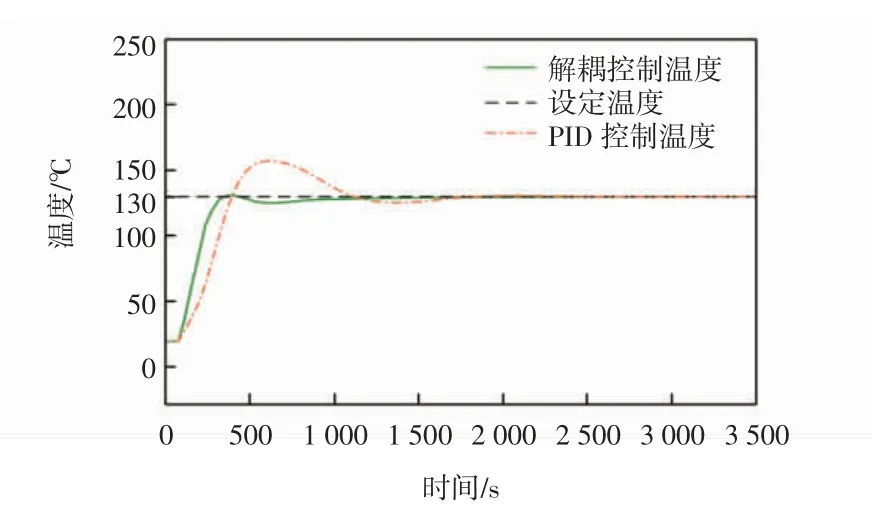
圖9 耦合系統與模糊解耦系統的溫度仿真結果Fig.9 Simulation results of temperature in coupled system and fuzzy decoupling system

圖10 耦合系統與模糊解耦系統的濕度仿真結果Fig.10 Simulation results of humidity in coupling system and fuzzy decoupling system

由圖9、圖10曲線可知：當使用傳統PID控制器對溫濕度進行控制時，溫度超調量達到23%，調節時間約為1 700 s；濕度的超調量為10%，調節時間為1 600 s左右。溫、濕度超調量過大在生產過程中是不被允許的，這會造成產品質量的不穩定，甚至會破壞生產設備。在使用模糊解耦控制時，溫濕度系統的超調量明顯下降，且震蕩平緩。溫度系統的調節時間由原來的1 700 s降低到1 100 s，且超調量幾乎為0；濕度系統的調節時間由原來的1 600 s降低至700 s，且超調量為0。解耦后的系統超調量小、穩態精度高，具有較好的動態響應特性和靜態特性，滿足系統的控制要求。

4.2 穩定性仿真

為驗證在加入解耦模塊后溫濕度控制系統的穩定性和抗干擾的能力，在2 700 s時分別給溫度回路和濕度回路一個干擾信號，來模擬實際工況下的環境干擾和人工干預，仿真結果如圖11、圖12所示。

圖11 耦合系統與模糊解耦系統加入干擾后的溫度仿真結果Fig.11 Temperature simulation results of coupled system and fuzzy decoupling system after adding interference

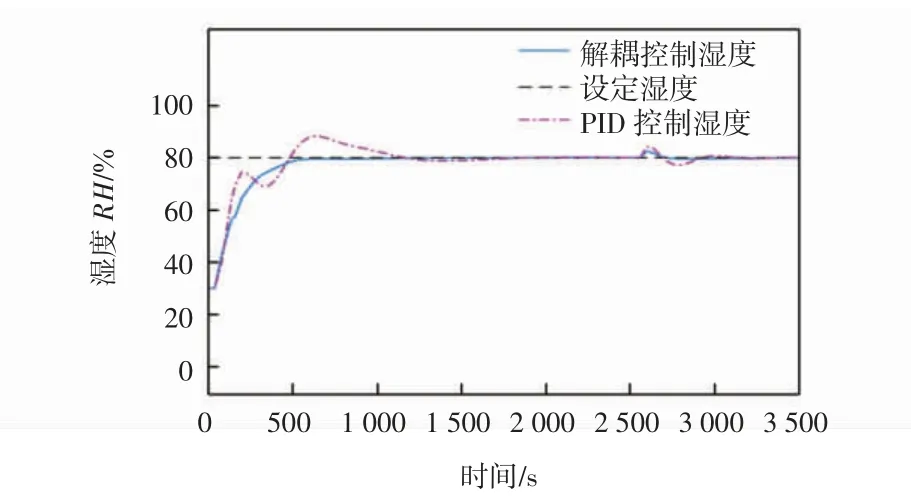
圖12 耦合系統與模糊解耦系統加入干擾后的濕度仿真結果Fig.12 Humidity simulation results of coupled system and fuzzy decoupling system after adding interference

由圖11、圖12曲線可知：當控制系統受到外界條件干擾或人為干預后，在使用傳統PID控制器控制時，溫度、濕度系統均震蕩明顯，且收斂緩慢；而在使用模糊解耦控制時，溫度、濕度受外界擾動的影響變小，且以更短的時間達到穩定值，魯棒性有了很大提升，說明模糊解耦控制器具有良好的擾動補償和抗干擾能力。

4.3 解耦效果仿真

對系統解耦效果進行驗證，在2 100 s時分別調整解耦系統和無解耦的工作溫度，將工作溫度由130℃調整至150℃，觀測溫度的變化和濕度是否存在耦合效應，仿真結果如圖13、圖14所示。

由圖13、圖14可知：在2 100 s時溫度控制器得到控制信號，將系統工作溫度由130℃調整至150℃。使用模糊解耦控制的溫度能夠迅速到達穩態，并且在解耦后濕度無明顯變化。在無解耦控制時，由于溫度的調節，濕度發生明顯的波動，在2 250 s時濕度的數值降低至72%，然后在2 500 s后重新到達相對濕度80%，濕度的波動量為10%。

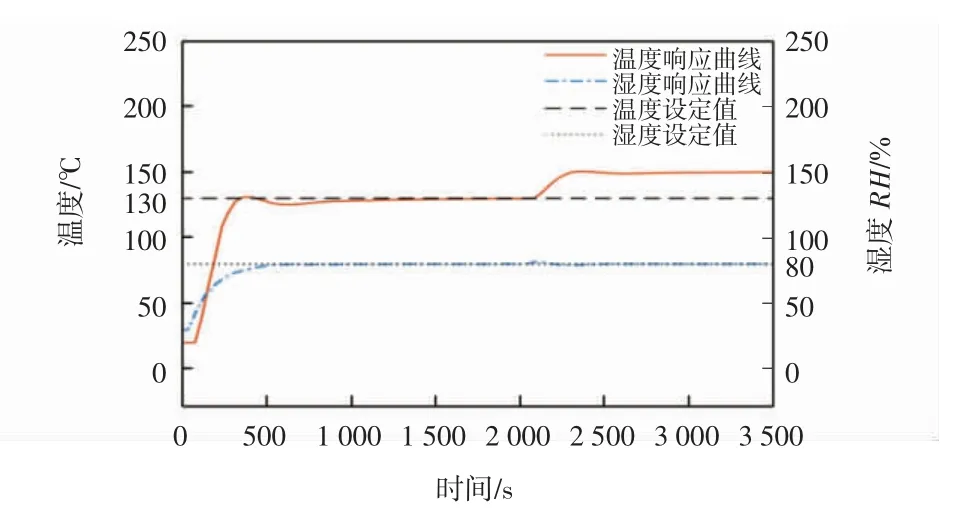
圖13 溫度調節后解耦系統響應曲線Fig.13 Response curve of decoupling system after temperature regulation

在2 100 s時對工作濕度進行調整，相對濕度由80%調節至90%，仿真結果如圖15、圖16所示。

由圖15、圖16可知：在2 100 s時濕度控制器接收調節信號，相對濕度由80%調節至90%，觀測溫度和濕度的變化。在使用模糊解耦控制時，濕度改變后溫度幾乎無變化；在無解偶控制時，由于濕度的調節，溫度在2 250 s時由130℃降低至120℃，并且在2 400 s時重新到達穩態，溫度的波動量為7%。

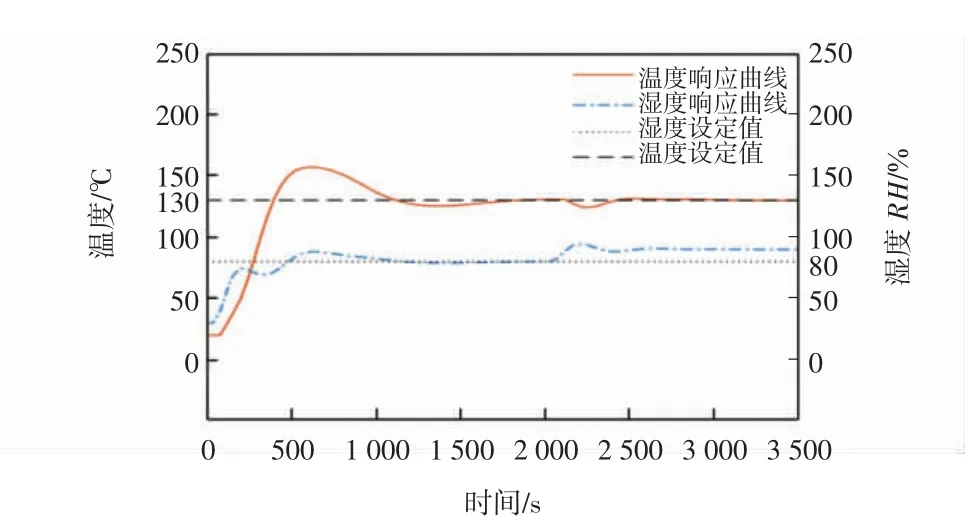
圖16 濕度調節后無解耦系統的響應曲線Fig.16 Response curve of undecoupling system after humidity regulation

5 結論

本文提出了基于模糊控制的解耦方案，使用Matlab對解耦系統和傳統PID系統仿真，得出如下結論：

（1）超調量方面，在使用PID控制時溫度超調量為23%，濕度超調量為10%；在加入模糊和解耦模塊后超調量幾乎為0。

（2）調節時間方面，使用PID控制時，溫度到達穩定時間為1 700 s，濕度到達穩定時間為1 600 s；當加入模糊和解耦模塊后，溫度到達穩態時間降低至1 100 s，濕度到達穩態時間降低至700 s。

（3）穩定性方面，在加入干擾時，使用傳統PID控制的溫濕度震蕩更加明顯，收斂緩慢；而使用模糊解耦控制時，震蕩相對平緩，收斂時間減小。

（4）溫、濕度耦合方面，在使用模糊解耦控制時，分別對溫度、濕度進行調節后，幾乎對系統沒有耦合影響；當使用無解耦控制時，溫濕度的耦合效應明顯。

綜上所述，對于溫、濕度這種具有強耦合、大遲滯的控制系統，模糊PID前饋解耦控制比傳統PID控制反應更靈敏、迅速，在加入干擾時擁有更好的魯棒性，并且在溫、濕度的控制過程中，達到了一定的解耦效果。