基于復卡爾曼濾波技術的華東區域風的多模式集成預報研究*

吳柏瑩 智協飛 陳超輝 張秀年

1 南京信息工程大學氣象災害預報預警與評估協同創新中心/氣象災害教育部重點實驗室，南京 210044 2 天氣在線氣象應用研究所，江蘇無錫 214000 3 國防科技大學氣象海洋學院，長沙 410073 4 云南省氣象臺，昆明 650034

提 要： 基于歐洲中期天氣預報中心的業務預報系統(EC)、美國國家環境預報中心的全球預報系統(GFS)、我國的中尺度數值業務預報系統(CMA-MESO)和全球預報系統(CMA-GFS)這4個預報系統的華東及周邊地區(20°～40°N、110°～130°E)2020年1—4月逐日地面和高空風的0～72 h預報資料，利用復卡爾曼濾波方法(augmented complex extended Kalman filter,ACEKF)對其進行多模式集成預報試驗，并對結果進行檢驗和評估。結果表明，ACEKF方法的預報效果優于多模式消除偏差集合平均、多模式超級集合預報等方法和單一模式的預報，能夠進一步降低風速預報的誤差，提高風場預報的預報準確率。ACEKF在高空風速預報上的改進效果要優于地面風速預報，在地形復雜地區改進效果更優，在所有預報時效的均方根誤差和距平相關系數上均有體現。

引 言

大氣是高度非線性的混沌系統、數值模式初始場具有不確定性、物理過程參數化方案還不夠完善，這幾點因素導致單一數值預報存在預報不確定性問題。集合預報技術基于大氣非線性運動使得傳統的確定性預報向概率預報轉變，從而能為用戶提供更全面完整的信息(Leith,1974)。

目前最具代表性的全球集合預報系統(global ensemble prediction system,GEPS)包括美國國家環境與預報中心，歐洲中期天氣預報中心和加拿大氣象局(Canadian Meteorological Centre,CMC)，這幾個中心所采用的初始擾動方法與集合預報結果都有一定差異，國內對集合預報的研究也方興未艾。田偉紅和莊世宇(2008)采用集合變換卡爾曼濾波(ensemble transform Kalman filter,ETKF)方法對我國的GRAPES預報模式做集合預報的擾動，取得一定效果。不同國家的模式在分辨率、參數化方案、資料同化等方面差異明顯，各有優劣。所以，如果能將各模式結果組合起來，整合優點，可以減小單個模式的系統誤差，多模式集成預報這個概念應運而生。Krishnamurti et al(1999)將多元線性回歸方法應用到多模式集成預報之中，這也是最早被提出的超級集合預報方法。經對比分析結果，超級集合預報提高了天氣尺度預報和季節尺度氣候預測的預報技巧，比單個模式的預報效果優秀。

多模式集成預報在我國的研究與應用雖然起步較晚，但也己取得許多成果。智協飛等(2009)基于TIGGE資料中氣溫這個物理量，進行不同地區的超級集合預報試驗，發現超級集合預報誤差比單模式預報減小很多。張涵斌等(2015)也集合了TIGGE下各模式預報資料，得到了西太平洋氣旋預報,效果較好。林春澤等(2009)發展了滑動訓練期消除偏差集合平均(running-bias removed ensemble mean,R-BREM)和滑動訓練期超級集合預報(running super-ensemble forecast, R-SUP)，訓練期每日向后滑動，使得每次預報的都為訓練期后一天的日期，降低了季節影響的誤差，預報效果優于固定的訓練期。在地面氣溫的延伸期預報中，崔慧慧和智協飛(2013)也證明了多模式集成能夠較好地改善單模式預報效果。Zhi et al(2012)研究了2007年北半球夏季地面2 m氣溫，其結果表明短期的預報(24～72 h)，超級集合的預報效果要遠優于單個模式的預報結果，而對于中短期的預報(96～168 h)，超級集合預報也能有效改善集合成員的預報結果。針對集合降水預報訂正，目前貝葉斯模式平均和頻率匹配訂正法業務上較為常用，已有不少研究。針對不同區域降水預報采用分級貝葉斯模式平均改進(Ji et al,2019；祁海霞等，2020)。頻率匹配訂正法在集合降水預報訂正上，明顯消除了大范圍小雨空報，提高了晴雨預報準確率，降水落區分布更加合理(智協飛和呂游，2019；李俊等，2015)。Ji et al(2020) 還采用基于目標的MODE評估(method for object-based diagnostic evaluation)對多模式降水預報進行集合，所得預報結果優于傳統的基于點對點評估的多模式超級集合預報。近年來，人工智能方法在科學計算、回歸預測模型上應用較廣。應用到多模式集成預報之中的神經網絡方法，也顯露一定的優勢。智協飛等(2020)和Peng et al(2020)利用淺層神經網絡、長短期記憶神經網絡、自然梯度提升等機器學習方法與傳統多模式集成預報方法進行對比，發現LSTM方法對于較長預報時效的地面氣溫預報改進效果較好，更多改進在我國西北、華北、東北等地區。上述研究均已充分證明了多模式集成預報的相對優越性，可用于業務預報中，更好地提高氣象服務水平。

卡爾曼濾波是一種根據觀測和預報數據自適應迭代權重系數減小誤差的有力工具。它的迭代計算過程較為簡單，線性擬合能力較強，對于噪聲的處理效果好，因此被廣泛應用。然而將卡爾曼濾波應用于多模式集成預報的研究目前并不多，尤其在氣象領域。基于衛星降水資料，Krishnamurti et al(2003)采用卡爾曼濾波，對衛星降水資料進行線性擬合，這也是該方法在氣象領域中的較早嘗試。隨后，Rixen et al(2009)、Rixen and Fevreira-Coelho(2007)與Lenartz et al(2010)利用卡爾曼濾波集合各個海洋模式的結果，對48 h海表溫度的預報也取得較好效果。智協飛和黃聞(2019)基于TIGGE資料集中多個模式預報的結果，利用卡爾曼濾波方法對氣溫和降水預報進行多模式集成預報研究，發現該方法對地面2 m氣溫和短預報時效的降水均有明顯改進。智協飛和趙忱(2020)將卡爾曼濾波技術和頻率匹配法相結合，對2016年夏季中國區域降水預報進行了訂正，發現降水落區預報和降水中心的量級預報效果均比其他多模式集成預報更加準確。近年來，數值模式日益提高了高低層大尺度變量(如500 hPa高度場、地面溫度等)的預報準確率。然而，對于風場的預報仍然存在較大誤差，并且風場作為一種具有二維變量的要素，除了對各分量進行預報，還需要考察矢量風場緯向和經向分量之間的聯系和配合，這也是目前風場預報存在不足的部分原因。He et al(2015)將卡爾曼濾波方法進行擴展變形，將臺風位置表示成復數，實部(虛部)表示臺風路徑的經度(緯度)，在臺風路徑的多模式集成預報中取得較好效果。這種適用于二維矢量訂正的復卡爾曼濾波方法在本文中被應用于風場的預報訂正。

盧曄等(2015)分析總結了華東區域風速變化特征。華東地區海岸線綿長，作為我國一大平原地帶，不僅地理位置特殊而且人口密集，對風場預報的準確預報對于航空和風能開發都具有重要的意義。本文對2020年1—4月華東區域地面和高空風速的預報資料進行多模式集成預報試驗。

1 資料與方法

1.1 資 料

1.1.1 模式預報資料

①歐洲中期天氣預報中心(European Centre for Medium-Range Weather Forecasts,ECMWF)風場預報資料(u,v)，地面水平分辨率為0.125°，高空各層水平分辨率為0.25°，逐日起報時間為12：00 UTC，預報時效為0～72 h，每隔3 h輸出一次預報結果。垂直層次主要包括700、850、925、950和1 000 hPa、地面10 m等。時間取2020年1月13日至4月13日。研究區域取20°～40°N、110°～130°E。

②同期、同區域中國氣象局的中尺度數值業務預報系統(CMA-MESO)風場預報資料，各層水平分辨率均為3 km，初始場時間間隔為24 h，逐日起報時間為12：00 UTC，預報時效為0～72 h，每隔3 h 輸出一次預報結果。垂直層次主要包括700、750、800、850、900、925、950、975和1 000 hPa、地面10 m等。

③同期、同區域美國國家環境預報中心的全球預報系統(Global Forecast System,GFS)風場預報資料，各層水平分辨率均為0.5°，初始場時間間隔為24 h，逐日起報時間為12：00 UTC，預報時效為0～72 h，每隔3 h輸出一次預報結果。垂直層次主要包括700、750、800、850、900、925、950、975和1 000 hPa、地面10 m等。

④同期、同區域中國氣象局全球預報系統(CMA-GFS)風場預報資料，各層水平分辨率均為0.25°，初始場時間間隔為24 h，逐日起報時間為12：00 UTC，預報時效為0～72 h，每隔3 h輸出一次預報結果。垂直層次主要包括700、800、850、925、975和1 000 hPa、地面10 m等。

1.1.2 再分析資料

用來評估模式預報技巧的觀測資料的質量、分辨率、覆蓋的地理范圍等都應考慮。實測站點資料能更好地反映真實物理量情況，能更加客觀地檢驗多模式集成預報，但是對于格點精度較高的預報資料，觀測資料存在不夠精細和缺測較多等缺點，容易導致額外的誤差。ERA5資料是ECMWF打造的最新一代再分析資料。孟憲貴等(2018)指出，ERA5在其前身ERA-Interim(Uppala et al,2008)的基礎上實現了很大升級，時空分辨率大幅提升，提供的變量增加到240種。所以經過綜合考量，本文選擇ERA5資料作為評估用“觀測”資料。

ERA5再分析資料：地面10 m水平分辨率為0.125°，高空各層水平分辨率為0.25°，高空垂直層次主要包括700,750,800,850,925,950,975和1 000 hPa 等。所取時間和區域同ECMWF預報資料。

1.2 方 法

1.2.1 數據預處理

由于各個模式預報資料及觀測資料的分辨率并不完全一致，為了得到華東地區更為精細化的氣象要素數據，在試驗之前需要對數據進行預處理和插值。本文先采用線性插值的方法將各中心預報數據的預報時效統一為0～72 h，各預報時效間隔為 1 h。對比后選取最優區域插值方法，將低分辨率的格點預報數據插值到高分辨率的網格上。本文將各模式地面預報值統一插值到0.125°×0.125°經緯網格上，高空預報值插值到0.25°×0.25°經緯網格上。將高空等壓面上風速數據插值到等位勢高度層(約為0～3 000 gpm，垂直方向間隔為300 gpm)，得到高空非常規層垂直風場。這樣處理的目的是能得到水平和垂直方向上高分辨率的風場預報資料，用于民航飛行的氣象保障。

得到統一的高時空分辨率風場資料后，再基于均方根誤差、距平相關系數等評估方法，采用簡單集合平均(ensemble mean,EMN)、消除偏差集合平均、超級集合預報、適用于矢量二維風場訂正的復卡爾曼濾波技術等方法對多模式預報數據進行集合。

1.2.2 反距離權重法插值

反距離權重法插值(inverse distance weight,IDW)，是按照目標站點與已有網格點間的距離反比分配權重，距離較近的數據點權重較高，距離較遠的數據點分配的權重較小。

(1)

式中：Z為目標站點的物理量要素，Zi為站點i的要素值，n為站點數，di為與第i個站點的距離，a為反比例系數(一般取2)。

1.2.3 多模式簡單集合平均

多模式簡單集合平均(EMN)對參與多模式集成的各模式預報結果進行簡單平均。計算公式如下：

(2)

式中：FEMN為經EMN方法集合后的預報值，N為預報模式的總數，Fi為模式i的預報值。

1.2.4 多模式超級集合預報和消除偏差集合平均

多模式超級集合預報(super-ensemble forecast,SUP)和多模式消除偏差集合平均(bias-removed ensemble mean,BREM)的公式如下所示：

(3)

(4)

本文都采用滑動訓練期方法(智協飛等，2009)，即設置一個最優長度的時間段為訓練期，逐日向后滑動，這樣能根據季節實時更替各模式預報權重，更為準確。

BREM和SUP的方法將整個時間段分成訓練期和預報期兩部分。本文經過調試，得到最優訓練期長度為40 d。采用滑動訓練期方法，2020年2月22日至4月13日設為預報期，2020年1月1日至2月21日設為訓練期，進行多模式集成試驗。例如：2020年2月22日的多模式集成預報結果就是訓練該日前40 d的預報數據。即2020年1月1日至2月21日為訓練期，在訓練期間計算出各個模式預報效果，在預報期中進行集合。

1.2.5 卡爾曼濾波和復卡爾曼濾波多模式集成方法

卡爾曼濾波不同于常見的線性的多模式集成預報方法，它是一種能夠根據每個時次的預報和觀測數據，自適應迭代各模式預報的權重系數的非線性方法。然而，即使采用滑動訓練期的方法，訓練期間的觀測值和預測值都是等價的。其實，觀測預報的重要性會隨著時間的推移而增加，即越接近預報時間，觀測預報的重要性就越大。因此，自動調整模態權系數的方法是非常有效的。這種想法與數據同化技術非常相似:在訓練期間，從最佳初始猜測場出發，確定權重系數；在增加新的觀測數據和預報數據時，立即調整權重系數；最后，確定權重系數并用于預測。然后當新的預測開始時，新的迭代又開始了。卡爾曼濾波長期以來被證明是消除系統誤差的有力工具，在數據同化領域得到了廣泛的應用。卡爾曼濾波的優點是可以自動適應模型與觀測值之間的差異以及非線性關系下的預測過程。

卡爾曼濾波的公式由預報和分析方程兩部分組成。

預報方程：

(5)

(6)

分析方程：

(7)

(8)

(9)

式中：上標f和a代表預報與分析狀態，下標t表示時刻。P為權重誤差協方差矩陣，Q與R分別為模式誤差協方差矩陣與觀測誤差協方差矩陣，它們均為對角陣。I代表單位向量，狀態向量W代表各個模式在預報期中的權重占比系數，其展開如下式所示：

(10)

式中：N與M分別代表參與的模式個數以及預報范圍內的格點總數。這里我們假設，上一步的分析權重Wa可作為下一步的預報權重Wf。

觀測算子H特殊排列了各個模式的預報值，Y包含了觀測值，式(8)中Y-HW為預報殘差，當每一新的起報時次的預報和觀測數據輸入的時候，Y-HW預報殘差會進行更新。卡爾曼增益K類似比例系數，當K趨于0時，權重系數趨于穩定，算法收斂。H的結構如下：

Ht=

(11)

式中：f(t)為模式預報。

P內元素之和隨著算法迭代將趨近于0，而Q始終保持不變。Q過大易導致算法不穩定，經過多次試驗發現Q<0.01時，最終的預報效果能夠達到最優，我們經驗性地設Q為0.01，在本文中我們選取訓練期間觀測值Y的標準差作為R。

水平風場是一種二維矢量場，我們將它分解為緯向風和經向風，某一點的水平風可以簡單地表示成復數，實部(虛部)表示緯向風(經向風)。該思路與臺風的復卡爾曼濾波方法(augmented complex extended Kalman filter,ACEKF)類似。在ACEKF中，所有的初始矩陣除了觀測算子H的長度變為2，寬度擴展了1倍之外，其余向量長度均擴展了1倍，寬度變為2。矩陣E為復卡爾曼濾波中矢量風場復數形式的示意，代表公式中的權重誤差協方差矩陣P、模式誤差協方差矩陣Q和觀測誤差協方差矩陣R。

(12)

相應的，預報期中的預報方程為：

(13)

式中St為最終預報結果。

1.3 評估與檢驗

1.3.1 均方根誤差

均方根誤差(root mean square error,RMSE)的計算如下：

(14)

式中:N是樣本總數，Fi為樣本i的預報值，Oi為樣本i的觀測值。RMSE的數值越小，實測值和預報值的差值越小，表明預報越準確。

1.3.2 距平相關系數

距平相關系數(anomaly correlation coefficient,ACC)的計算如下：

(15)

2 單個模式風速預報的檢驗評估

首先以均方根誤差為評估指標來對比各個模式的預報效果。如圖 1所示，分別計算了4個模式(ECMWF、GFS、CMA-GFS、CMA-MESO)在預報期內華東區域預報時效為24 h、時間平均的地面10 mu、v、全風速預報的均方根誤差的地理分布。

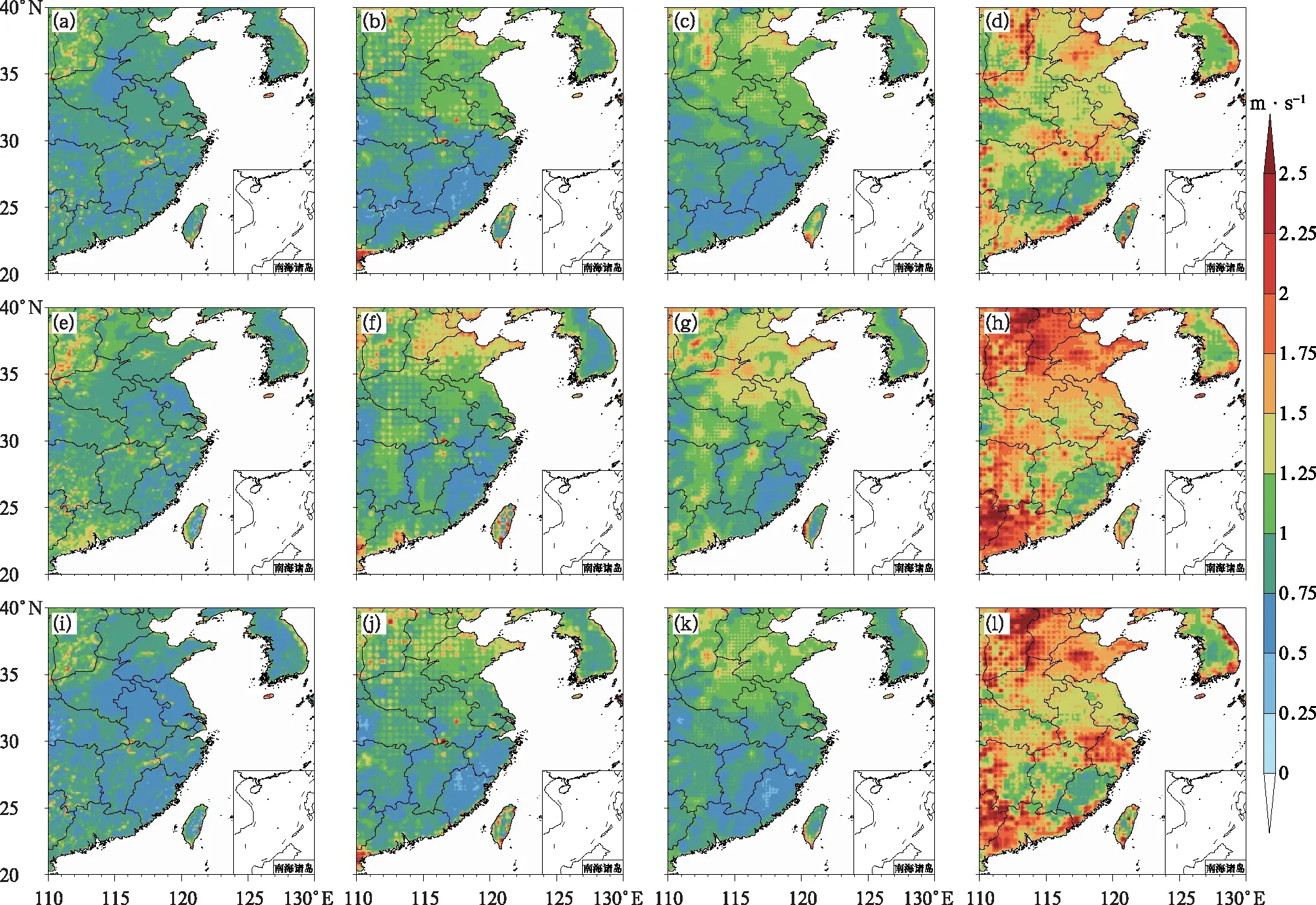
圖1 預報期內華東地區24 h預報時效平均地面10 m(a～d)緯向風u、(e～h)經向風v、(i～l)全風速的(a,e,i)EC、(b,f,j)GFS、(c,g,k)CMA-GFS、(d, h, l)CMA-MESO模式預報的時間平均均方根誤差的地理分布Fig.1 Geographical distribution of time average RMSE with 24 h lead time averaged surface 10 m (a-d) zonal wind, (e-h) meridional wind, and (i-l) total wind speed for (a, e, i) EC， (b, f, j) GFS， (c, g, k) CMA-GFS， and (d, h, l) CMA-MESO in East China during the averaged forecast period

在幾個單模式中，ECMWF(簡稱EC)、GFS及CMA-GFS的預報技巧評分較高，其中EC模式預報的誤差最小，GFS次之，誤差分布表現穩定，CMA-MESO模式的預報技巧較差。誤差最小的EC模式在區域分布上RMSE相較于CMA-MESO平均低了1.5 m·s-1左右。從整個華東地區來看，4個模式對風速預報的誤差的地理分布較為一致，大體顯示出緯度從低到高RMSE逐漸增加的趨勢。山東及廣東、福建沿海地區均方根誤差較大，長江以南內陸地區均方根誤差較小。

EC模式評分表現最好，后續將應用多模式集成技術，將預報技巧最優的單模式與傳統的多模式集成、復卡爾曼濾波方法進行對比分析。

3 多模式風速集成預報結果分析

為更好研究華東地區對精細化風場的預報能力，圖2選取預報期內EMN、BREM、SUP、ACEKF方法及EC模式在預報時效為24 h的地面10 m風速預報的平均RMSE進行比較分析。由圖2可知，EMN、BREM方法預報效果較差，在山東及廣東部分地區地面風速RMSE較大，約為1.5 m·s-1。不等權的多模式集成預報中，SUP方法的預報效果有一定改進，ACEKF預報效果最好，華東地區誤差明顯減小。

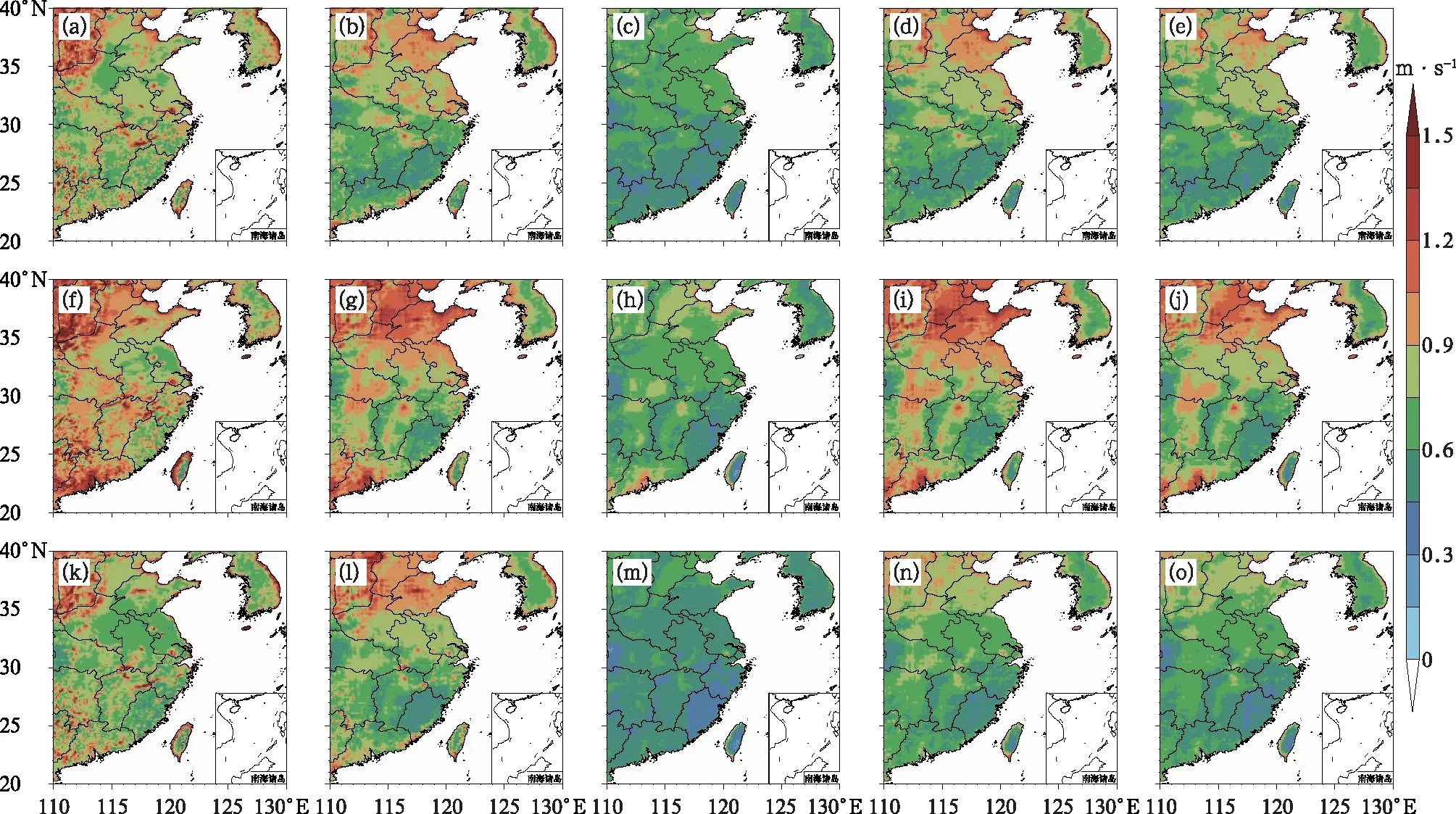
圖2 預報期內華東地區24 h預報時效平均地面10 m(a～e)緯向風u、(f～j)經向風v、(k～o)全風速的(a,f,k)EC、(b,g,l)EMN、(c,h,m)ACEKF、(d,i,n)BREM、(e,j,o)SUP預報的均方根誤差的地理分布Fig.2 Geographical distribution of RMSE with 24 h lead time averaged surface 10 m (a-e) zonal wind, (f-j) meridional wind, and (k-o) total wind speed for (a, f, k) EC、 (b, g, l) EMN, (c, h, m) ACEKF, (d, i, n) BREM, and (e, j, o) SUP in East China during the averaged forecast period

為了進一步討論ACEKF預報的優越性，我們計算了地面10 m ACEKF預報相較其他多模式集成方法和單模式預報的均方根誤差減小的百分比(圖3)。ACEKF相較EMN方法，改進率最高。在廣東沿海、福建地區、江淮地區地面風場ACEKF預報改進效果最好，改進率約為40%，華東地區平均地面10 m風速預報RMSE改進率在20%左右。

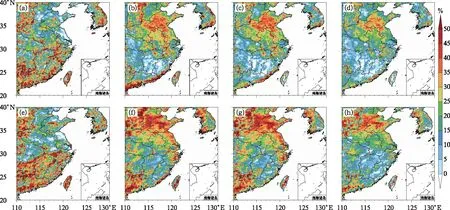
圖3 預報期內華東區域24 h預報時效的地面10 m(a～d)緯向風u、(e～h)經向風v、(i～l)全風速的ACEKF相較(a,e,i)EC、(b,f,j)EMN、(c,g,k)BREM、(d,h,l)SUP預報的時間平均均方根誤差改進率的地理分布Fig.3 Geographical distribution of the improvement rate of time average RMSE with 24 h lead time of ACEKF on surface 10 m (a-d) zonal wind u, (e-h) meridional wind v and (i-l) total wind speed in East China during the averaged forecast period compared with (a, e, i) EC, (b, f, j) EMN, (c, g, k) BREM, and (d, h, l) SUP

續圖3Continued

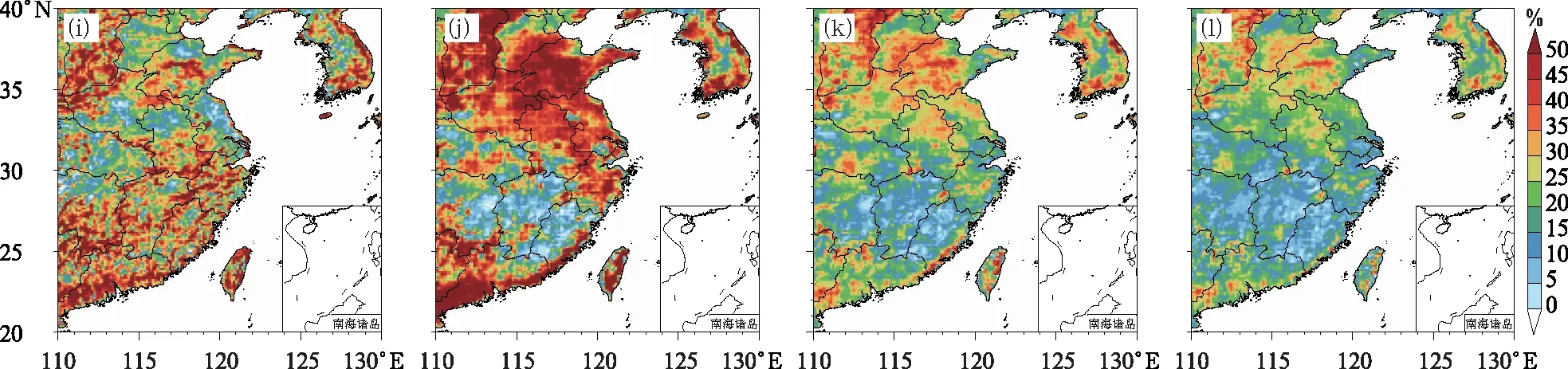
圖4選取高空具有代表性的幾個位勢高度層, 對比了300、1 500、2 100、3 000 gpm的預報期內各模式緯向風速24 h預報的平均均方根誤差。同地面10 m的結果一樣，ACEKF方法預報效果最好，SUP方法次之。ACEKF方法在2 100 gpm高度層上預報均方根誤差最大，也與前面機場預報誤差的垂直廓線一致。圖5是ACEKF方法較其他多模式集成預報方法和EC單模式預報的均方根誤差減小的百分比。以300 gpm為例，華東地區平均預報均方根誤差改進率在53%左右，ACEKF對高空風場預報的改進效果要優于地面風場。

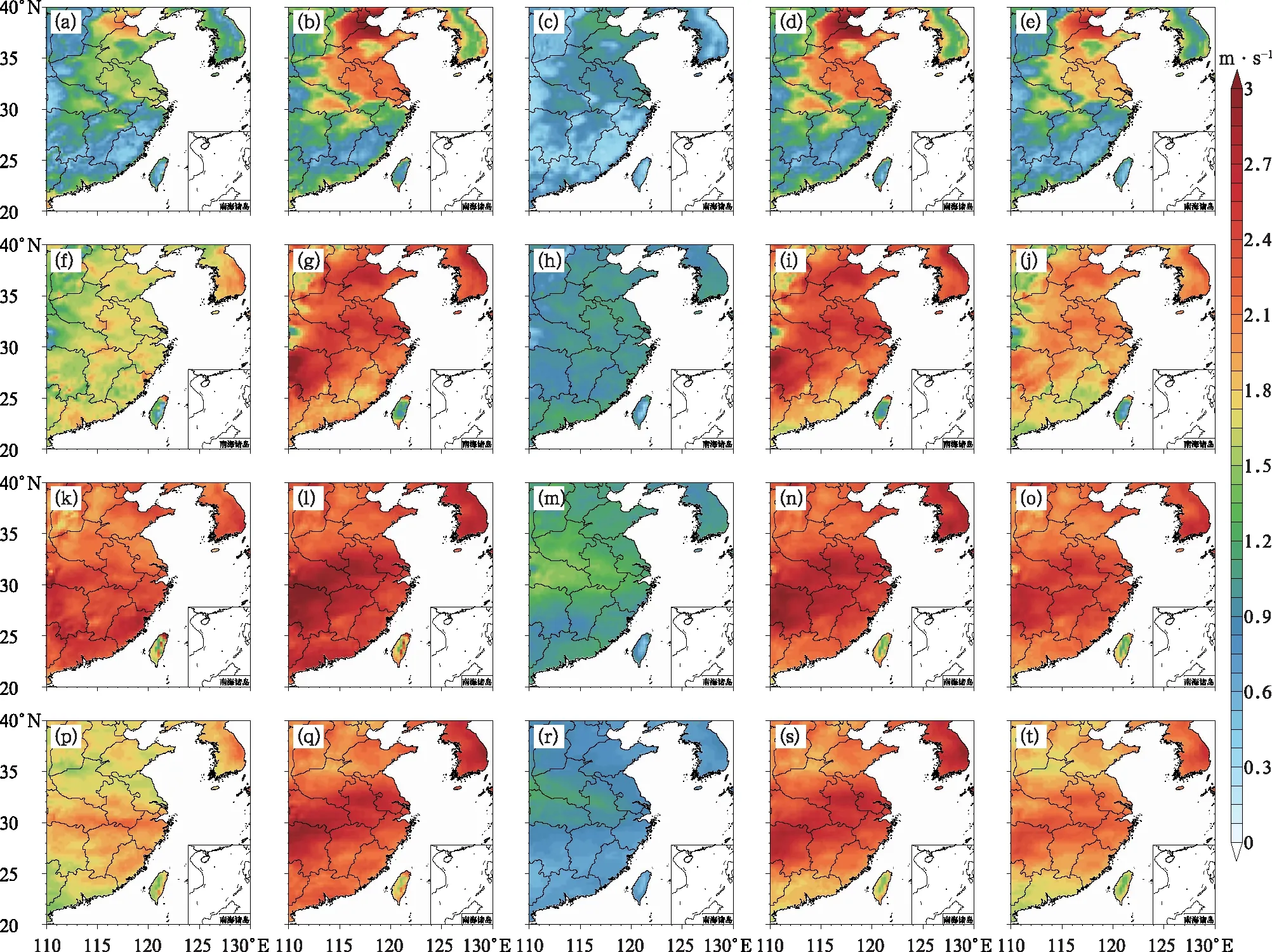
圖4 預報期內華東區域24 h預報時效的(a～e)高空300 gpm、(f～j)1 500 gpm、(k～o)2 100 gpm、(p～t)3 000 gpm緯向風u的(a,f,k,p)EC、(b,g,l,q)EMN、(c,h,m,r)ACEKF、(d,i,n,s)BREM、(e,j,o,t)SUP預報的時間平均均方根誤差的地理分布Fig.4 Geographical distribution of time average RMSE with 24 h lead time of (a, f, k, p) EC, (b, g, l, q) EMN, (c, h, m, r) ACEKF, (d, i, n, s) BREM, and (e, j, o, t) SUP of (a-e) 300 gpm, (f-j) 1 500 gpm, (k-o) 2 100 gpm, (p-t) 3 000 gpm zonal wind u of East China during the averaged forecast period

圖5 同圖3，但為高空300 gpmFig.5 Same as Fig.3, but on 300 gpm

圖6、圖7為預報期內華東地區地面10 m和高空各層風速預報的平均均方根誤差和距平相關系數(時間和空間上求平均)，BREM、EMN均方根誤差相比于EC預報略高，距平相關系數略低，SUP和EC預報技巧相差無幾，ACEKF方法預報效果最優。因區域較小、時間段較短，模式預報總體均方根誤差較小、距平相關系數較高。隨著預報時效延長，ACEKF方法優勢更加明顯，預報時效為72 h，ACEKF相比BREM方法，均方根誤差約改進1.3 m·s-1，距平相關系數提高0.1左右。ACEKF方法對高空預報的改進效果優于對地面預報的改進效果。

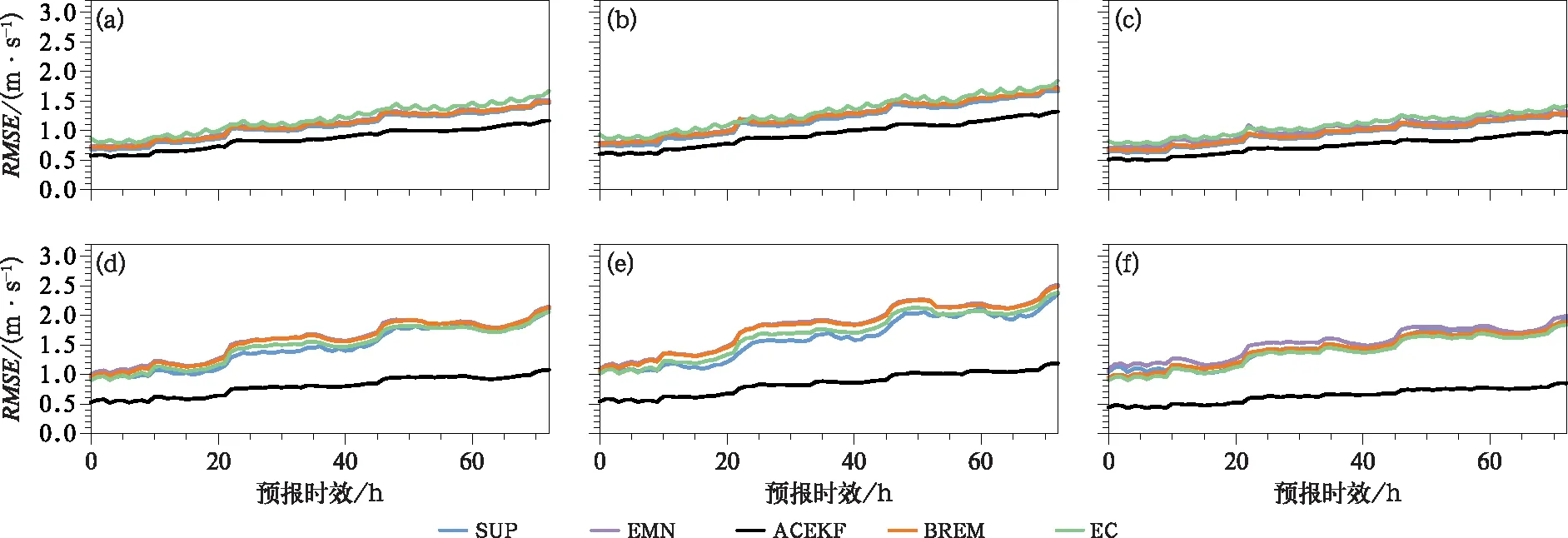
圖6 預報期內華東區域不同預報時效的(a～c)地面10 m、(d～f)高空300 gpm、(g～i)1 500 gpm、(j～l)3 000 gpm的(a,d,g,j)緯向風u、(b,e,h,k)經向風v、(c,f,i,l)全風速的EC、EMN、ACEKF、BREM、SUP預報的區域、時間平均均方根誤差折線圖Fig.6 Area and time average RMSE of EC, EMN, ACEKF, BREM and SUP forecasts of (a-c) surface 10 m, (d-f) 300 gpm, (g-i) 1 500 gpm, (j-l) 3 000 gpm (a, d, g, j) zonal wind u, (b, e, h, k) meridional wind v and (c, f, i, l) total wind speed in East China during the forecast period at different lead times

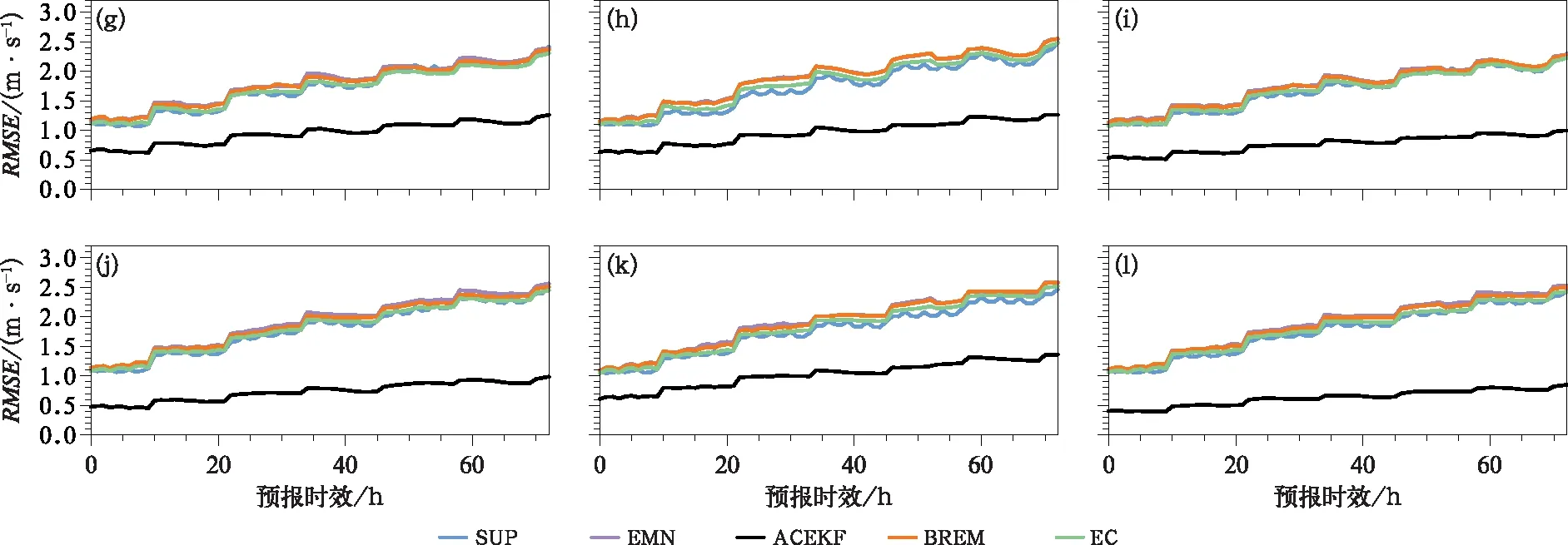
續圖6Continued

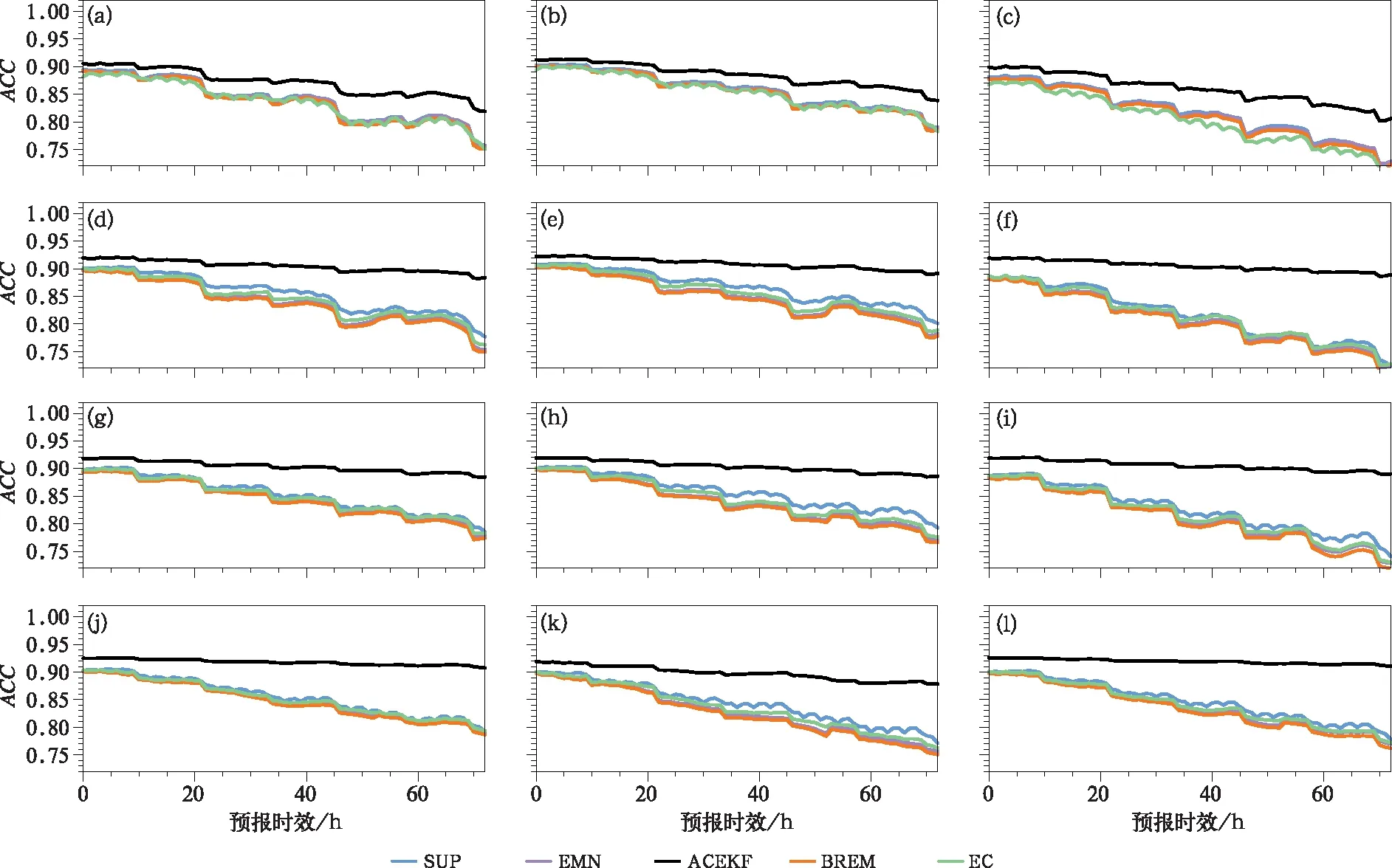
圖7 同圖6，但為距平相關系數Fig.7 Same as Fig.6, but for ACC

圖8、圖9分別為地面10 m和高空300 gpm 24 h風預報均方根誤差隨預報時效和起報日的變化。地面24 h風速預報的RMSE基本小于1 m·s-1，誤差隨預報時效延長而增長。ACEKF方法對高空300 gpm風預報具有明顯改進，比其他多模式集成預報以及EC單模式預報技巧都有很大改進。ACEKF方法對于預報的穩定性也有一定改進。在預報期的第12日，也就是2020年3月4日時模式預報誤差比較大，這一天有持續陰雨和大風預警。運用復卡爾曼濾波多模式集成對預報進行集合后對風速預報的改善比較明顯。

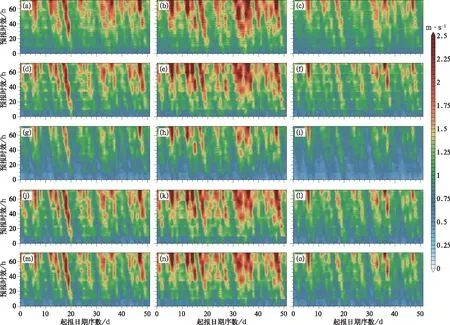
圖8 預報期內華東區域地面10 m(a,d,g,j,m)緯向風u、(b,e,h,k,n)經向風v、(c,f,i,l,o)全風速的(a～c) EC、(d～f)EMN、(g～i)ACEKF、(j～l)BREM、(m～o)SUP預報的區域平均的均方根誤差隨起報日、預報時效的變化Fig.8 Distribution of RMSE with time and forecast lead time for the regional average of (a-c) EC, (d-f) EMN, (g-i) ACEKF, (j-l) BREM, (m-o) SUP forecast in East China during the forecast period of 10 m (a, d, g, j, m) zonal wind u, (b, e, h, k, n) meridional wind v and (c, f, i, l, o) total wind speed

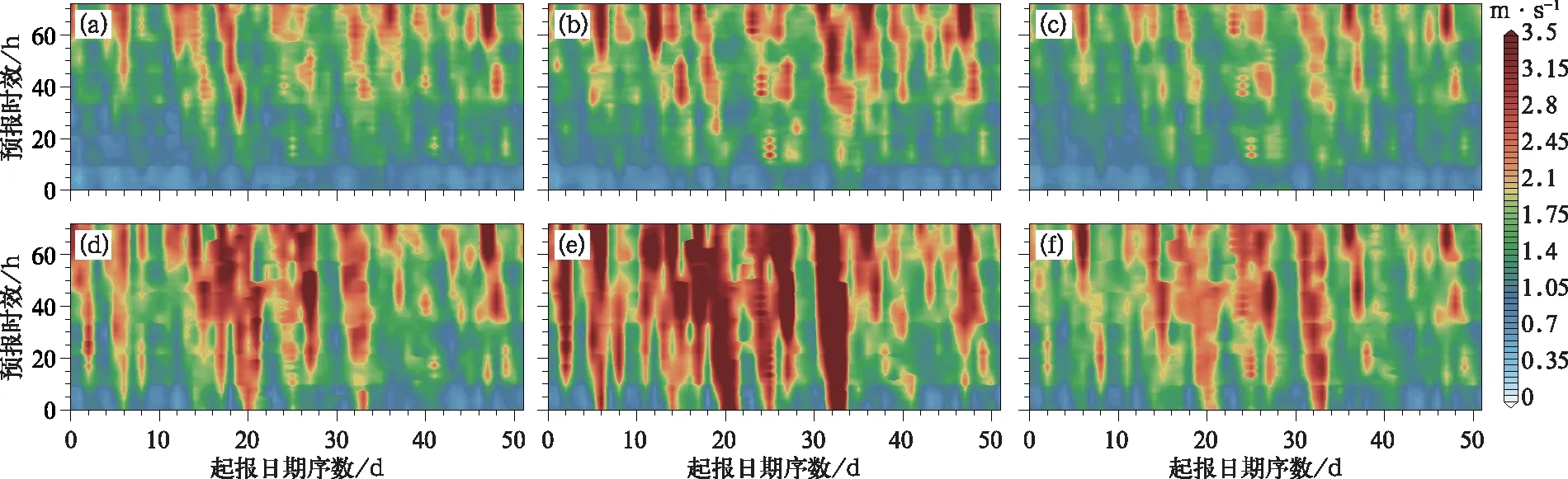
圖9 同圖8，但為高空300 gpmFig.9 Same as Fig.8, but for 300 gpm

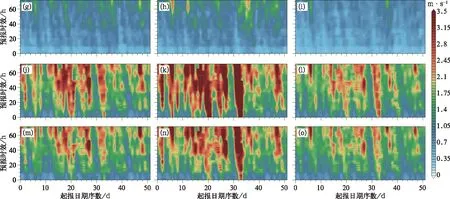
續圖9Continued

4 結論與討論

本文利用簡單集合平均、滑動訓練期消除偏差集合平均、多模式超級集合預報和復卡爾曼濾波幾種方法對EC、GFS、CMA-MESO和CMA-GFS共4個模式預報的0～72 h地面、高空風預報進行多模式集成，得到以下幾點結論：

(1)ACEKF能夠進一步減小風場預報的誤差，提高預報技巧，在緯向風、經向風、全風速預報上均有體現。

(2)從風場預報結果來看，無論是對地面10 m風預報還是高空風預報，ACEKF對經向風預報的改進效果都要優于緯向風預報，在預報RMSE和ACC上都有反映。

(3)ACEKF對高空風場預報的改進效果要優于地面風場，對高空風速預報的改進率可達53%左右，而對地面風速預報的改進率只有約20%。

(4)隨著預報時效延長，風場預報誤差增大，但ACEKF方法對風場預報改進效果更為明顯。

致謝：本文的結果是在南京信息工程大學高性能計算中心計算獲得的，在此表示由衷感謝！