瑞利-伯納德熱湍流中的多湍流態現象

陳 鑫，郗恒東

(1. 上海大學 力學與工程科學學院，上海市應用數學和力學研究所，上海 200072；2. 西北工業大學 航空學院，西安 710072；3. 西北工業大學 極端力學研究院，西安 710072)

0 引 言

由溫度梯度引發的湍流稱為熱湍流。熱湍流在自然界和生產生活中普遍存在并起著至關重要的作用：在自然界中引起天氣、氣候變化的大氣環流、海洋環流，引起大陸板塊漂移的地幔對流，決定地磁場產生和變化的外地核對流等；在日常生活中的燒開水以及室內供暖；在工業生產中影響單晶晶體生長和金屬制備過程中的對流、核反應堆內部及其乏燃料池中的對流等。人們針對這一類流動現象提出了一種模型系統，稱之為瑞利-伯納德（Rayleigh-Bénard，RB）熱湍流系統[1-3]。

圖1為矩形瑞利-伯納德熱湍流系統的示意圖。瑞利-伯納德熱湍流系統是一個高度為H的封閉湍流系統，加熱其下壁，保持溫度T+ΔT，冷卻其上壁，保持溫度T，側壁為絕熱壁。整個熱湍流系統中充滿了流體介質，流體介質在上、下壁間溫差ΔT的作用下，下（上）壁附近的流體受熱膨脹（遇冷收縮），密度減小（變大），受到浮力的作用，從下（上）壁附近熱（冷）的熱邊界層中脫落，形成高（低）于湍流背景溫度的蘑菇狀羽流結構。當系統的控制參數Rayleigh數（Ra）、Prandtl數（Pr）、寬高比（Γ=L/H）進入一定的參數空間時，羽流由于羽流之間的相互作用最終自組織形成大尺度的相干結構，即大尺度環流（Large-Scale Circulation，LSC）[4-5]。理解熱湍流系統中相干結構的動力學特征有助于理解湍流熱輸運、邊界層結構以及湍流脈動等重要問題。

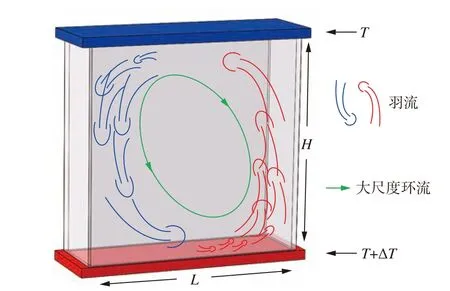
圖1 矩形瑞利-伯納德熱湍流系統和流動示意圖(紅色代表高溫流體，藍色代表低溫流體，綠色箭頭指明了大尺度環流的流動方向)Fig. 1 (Color online) Sketch of a rectangular turbulent RB convection(The red-arrows and blue arrows indicate the hot and cold plumes respectively. The green arrow represents the direction of the large-scale circulation)

2008年，郗恒東與夏克青首次在圓柱形瑞利-伯納德熱湍流系統中通過實驗發現了熱湍流系統中的多湍流態現象[6]，即在相同的控制參數下，系統的大尺度流動存在不同的湍流狀態（結構），而且不同的湍流狀態可以自發地切換。對于流動在某一確定的控制參數下所處的流動狀態， Kolmogorov在1941年提出的湍流理論[7]認為，對于充分發展的湍流，其脈動足夠大以至于流動會遍歷所有的相空間，因而這種充分發展湍流的小尺度統計特性應只存在一種統計穩定的狀態。經典的湍流理論假設湍流是各態遍歷的，也就是說即使某些中間狀態可能會受到例如初始條件等因素的影響，但是其統計平均量是不依賴于初始流場的。各態遍歷假設是湍流理論的一個重要基礎。大尺度流動的多湍流態的發現及其進一步的研究，勢必會為經典的湍流理論提供一個強有力的補充。近年來這種多湍流態現象陸續在不同的湍流系統中被發現并且被廣泛且細致的研究，除了本文所描述的熱湍流系統[6,8-20]，還包括泰勒-庫埃特湍流系統[21-22]、雙擴散對流湍流系統[23]、馮·卡門湍流系統[24]、旋轉球殼庫埃特流動系統[25]、展向旋轉平板庫埃特湍流系統[26]、二維強迫剪切流動[27]、二維槽道流動[28]、風洞中流經作鐘擺運動的圓盤后的流動[29]以及T型混合器中的流動[30]等。在上述的研究中，一個普遍的發現是當系統處于不同的湍流狀態時，系統中的大尺度相干結構存在顯著的差異，同時系統的某些輸出參數，例如系統整體的能量輸運效率、動量輸運效率或者流動的摻混效率等，也有顯著的不同。早先對于湍流相干結構的研究告訴我們，湍流結構是湍流基本物理過程的流場時空分布表征，湍流結構的時空演化直接主導了流體的動量、能量和物質的輸運特性，因而對湍流中力、熱的產生及其非定常輸運起著決定性的作用。因此，知曉在某一控制參數下，系統處于何種流動狀態對理解、進而調控此時系統的動量、能量以及物質的輸運特性是十分關鍵的。

此外，多湍流態現象在自然界的流動中也有展現。在海洋環流中，一個典型的例子是日本東海岸的“黑潮”，這是與北大西洋灣流齊名的一支強大的暖性海流。“黑潮”時不時會改變其沿著日本東海岸自南向北的流動方向，轉頭回流，出現所謂的“大蛇行”現象[31]，進而引發西太平洋地區一系列的海洋生態問題，最近一次“大蛇行”發生在2017年8月。再者，例如在地球的大氣環流中，中緯度地區的大氣以西風為主且幾乎是帶狀流動，然而，這種西風流動會被突然出現并可以持續很長時間的反氣旋流動阻擋，從而向極地明顯偏移[32]。此外，外地核中的液態金屬的對流[33]也存在著流動反向的現象。多湍流態現象不僅在地球上的大氣、海洋和外地核的流動中出現，在木星大氣中也有出現，其對流層中的條帶狀的射流流動在1939年至1940年間失去了其中一股，取而代之的是三個呈現白色的反氣旋流動，這一事件被稱為木星氣候突變事件[34]，這也可以認為是一種新的湍流狀態。

本文將就瑞利-伯納德熱湍流系統中多湍流態現象的研究成果進行綜述。通過近些年的研究發現，多湍流態現象大致可以分為兩類：一類是在相同的初始條件下，隨著流動的發展，流動在不同的湍流狀態下自發地、隨機地切換，上一段中提到的自然界中的多湍流態現象目前來看也均屬于這一類；另一類則是由于在流動初始時刻給定了不同的初始條件進而導致系統演化為不同的流動狀態，并且該流動狀態十分的穩定，可以保持很長的一段時間。下文中，我們將就瑞利-伯納德熱湍流系統中這兩類多湍流態現象分別展開介紹。在本文的最后，我們將給出總結與展望。

1 相同參數條件下自發產生的多湍流態現象

我們首先討論相同參數條件下自發產生的多湍流態現象。郗恒東與夏克青[6]最早在圓柱形熱湍流系統中通過實驗發現了該類型的多湍流態現象。他們通過實驗分別研究了寬高比為1、1/2和1/3的熱湍流系統中的流動結構隨時間的演化規律，發現在這三個寬高比的熱湍流系統中，單環的大尺度環流模態（single-roll state, SRS，可見圖2（c）、圖3 （a））和上下堆疊排列的雙環模態（double-roll state，DRS，可見圖2（c）、圖3 （b））均可以穩定存在，且這兩種流動狀態可以自發地、隨機地相互轉換。

圖2展示了在對流腔體的上（3H/4）、中（H/2）、下（H/4）三個不同高度上通過多點溫度測量方法測得的流動在單環模態與雙環模態之間的一次轉變。多點溫度測量方法是由Cioni等[35]提出并在之后相關的研究中被廣泛使用[36-38]。眾所周知，大尺度環流實際上是冷、熱羽流的自組織運動[39]，基于此，對于圓柱形熱湍流系統，我們可以在某一橫截面周向均勻地布置若干（此處使用8個）溫度探頭，通過使用函數Tn=T0+Acos(nΠ/4?φ)，n= 0，···，7，擬合某一瞬時時刻測得的8個周向溫度值，可以獲得大尺度環流的瞬時方位角φ以及大尺度環流的瞬時強度A。從圖2可以看到，在150 s之前，我們可以觀察到上、中、下三層測得的大尺度環流平面的方位角幾乎重合，說明此時系統內的流動呈現一個尺寸與系統尺寸相若的單環結構，如圖2（c）中的左側示意圖所示。在150 s左右，Atop的值降低至0附近，緊接著，φtop的值突變了180°，即當地大尺度環流的方位角發生了反向。結合Atop、φtop的變化，說明原先的大尺度環流在系統的上部出現了分裂，形成了一個新的相反流動的渦結構。我們還注意到φmid、φbot的值從始至終都較為接近，這說明分裂之后的上、下兩個渦并非是對稱的，下方的渦結構尺寸要大于上方的渦結構，如圖2（c）中的中間示意圖所示。流動在雙環模態下保持了一段時間之后再次回到了原先方向的單環模態。當然，這里新形成的單環模態也不總是保持原先的流動方向，有時也會形成相反方向的單環流動。

圖3是利用粒子圖像測速技術（PIV）測得的速度場，展示了一次單環模態-雙環模態-單環模態的轉變過程。從圖中可以清晰地看到在t= 0s時，流動呈現一個傾斜的大尺度環流，即單環結構；隨后，在t= 72 s時，流動自單環模態破裂為上、下堆疊的兩個渦，并且下方的渦結構尺寸更大；在t= 184 s時，流動又恢復到單環結構。這樣的轉變過程與通過多點溫度測量方法測得的結果一致。

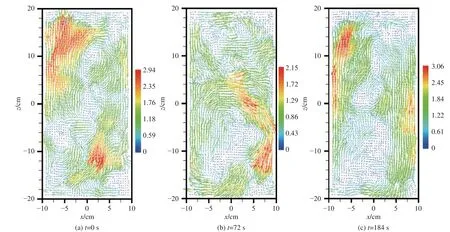
圖3 Ra = 5.3×1010, Γ = 1/2，利用粒子圖像測速技術（PIV）測得的流動狀態隨時間演化的瞬時速度場[6]：(a) 單環模態(SRS)；(b) 雙環模態(DRS)；(c) 再次回到單環模態Fig. 3 (Color online) PIV-measured instantaneous velocity vector fields showing a flow mode transition in Γ = 1/2 cell at Ra = 5.3×1010[6]:(a) single-roll mode (SRM); (b) double-roll mode (DRM); and (c) single-roll mode again

此外，該工作還研究了寬高比對多湍流態的影響，發現寬高比影響不同湍流態（結構）持續存在的時間。Γ= 1時，約87.1%的時間系統流動處于單環模態，僅有0.8%的時間流動處于雙環模態；而當Γ=1/2時，單環模態所占的時間降低至69.5%，雙環模態則上升至7.9%；當Γ= 1/3時，單環模態所占的時間進一步下降，至26.7%，雙環模態則進一步上升，并超越單環模態，達到了34.1%。此外，通過細致地測量系統的傳熱效率，他們發現當流動在不同的流動狀態之間切換時，系統的傳熱效率也相應地變化。通過直接比較系統處于不同流動狀態時的傳熱效率（無量綱的熱輸運效率Nusselt數（Nu）），他們發現，單環模態相較于雙環模態更有利于傳熱。

隨后，Weiss和Ahlers[10]延續了郗恒東和夏克青的工作，單獨針對Γ= 1/2的熱湍流系統進行了更為細致且系統的研究。首先，他們在實驗中同樣觀測到了郗恒東和夏克青[6]發現的多湍流態現象。之后，他們研究了不同湍流態存在的時間與Ra數之間的依賴關系，他們發現單環模態所占的時間隨著Ra數的增長逐漸從12%（Ra= 2×108）提升至80%（Ra= 1011），雙環模態則相應的由40%降低至6%。此外，他們也證實了郗恒東等[6]提出的單環模態相較于雙環模態更有利于熱量輸運的結論。圖4（a）展示了系統傳熱效率Nu(t)與流動所處湍流態之間的互相關，從圖中可以發現單環模態的強度與傳熱效率呈現正相關，證明單環模態更有利于傳熱，而雙環模態的強度則與傳熱效率呈現負相關，證明其不利于傳熱。圖4（b）則進一步定量地給出了單環模態相較于雙環模態傳熱效率增加的幅度，在Ra= 1010（1011）時，單環模態的傳熱效率比雙環模態的傳熱效率高1.6%（0.9%）。

圖4 (a) Ra = 9.0×1010，Γ = 1/2，系統傳熱效率Nu(t)與流動狀態參數S(t)之間的互相關，紅色實線代表單環結構(SRS)，藍色虛線代表雙環結構(DRS)；(b) 歸一化后的單環結構傳熱效率與雙環結構傳熱效率的差別，圖中實線為對數據的冪律擬合，得到的冪指數為-0.25±0.07. 圖取自參考文獻[10]Fig. 4 (Color online) (a) Time cross-correlation functions between Nu(t) and the state function S(t) for the SRS (solid red line) and the DRS (dashed blue line), These results are for Ra =9.0×1010，Γ = 1/2; (b) Normalized differences in Nu between the SRS and the DRS on logarithmic scales. The solid line is a powerlaw fit which yielded the exponent -0.25±0.07. The figure is adapted from Ref.[10]

Zwirner等[18]在更小寬高比（Γ= 1/5）的圓柱形熱湍流系統中利用直接數值模擬同樣發現，在相同的控制參數下，存在單環模態以及雙環模態兩種可以穩定存在的流動狀態，并且他們指出雙環模態的傳熱效率僅為單環模態的80%，這個數值比實驗中測量得到的數值（約1%～2%）要大很多。最近，Zwirner等[19]進一步利用直接數值模擬探索了在Γ= 1/5的圓柱形熱湍流系統中的多湍流態現象及其產生的原因。他們發現在Ra= 5×106，Pr= 0.1，Γ= 1/5時，不僅存在單環模態、雙環模態，還會存在上下堆疊排列的三環、四環模態（可見圖5（a～d））。同時，他們發現流動中渦環的數量越多，傳熱效率也相應的越低，在Ra=5×106時，單環模態的傳熱效率是四環模態傳熱效率的2.5倍。此外，他們還發現此時的流動更傾向于處在雙環模態，其存在的時間占比達到了40.6%。在該參數下，單環、雙環、三環以及四環模態平均存活時間（以系統特征時間歸一化）、各種流動模態平均存在時間占比以及傳熱效率可見表1。

表1 Ra = 5×106，Pr = 0.1，Γ = 1/5，單環、雙環、三環以及四環模態平均存活時間(使用系統特征時間歸一化)、平均存在時間占比以及傳熱效率Nu [19]Table 1 Mean lifetime, probabilities, and mean heat transport efficiency Nu of n-roll flow modes (n = 1, 2, 3, 4), for Ra = 5×106,Pr = 0.1, Γ = 1/5

關于多湍流態發生的原因，Zwirner等認為是由于單環結構大尺度環流的橢圓不穩定性，定量的分析也支持他們這一結論。橢圓不穩定性是指由具有橢圓形流線的二維平面流動破裂產生三維流動的失穩機理（可見綜述論文[40]）。在Γ= 1/5的熱湍流系統中，當流動處于單環模態時（如圖5（a）所示），可以被認為是一個具有橢圓形流線的二維平面流動，當其受到一定的擾動時，橢圓不穩定性將會引起其破裂，從而產生多環模態。圖5（e）展示了一個單環流動破裂過程中的瞬時場，從該流場中可以看到很強烈的周向運動，正是這樣的周向運動破壞了單環結構的大尺度環流。針對這樣的模態間轉變機制，Zwirner等認為只有當橢圓不穩定性的增長率遠大于系統中黏性耗散引起的阻尼（可簡單認為是維持當前流動狀態的穩定項）時才能發生。事實上也正是如此，Zwirner等發現在該參數下，橢圓不穩定性的增長率要遠遠大于其他的穩定性項。

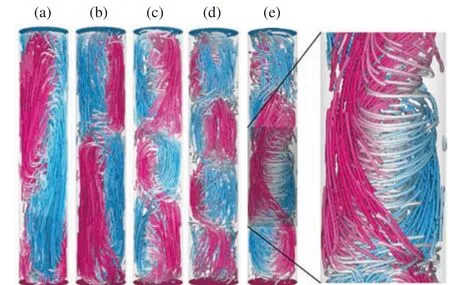
圖5 Ra = 5×106，Pr = 0.1，Γ = 1/5，大尺度環流的瞬時流線圖[19]：(a) 單環結構；(b) 雙環結構；(c) 三環結構；(d) 四環結構；(e) 由于橢圓不穩定性而產生的強烈的周向流動Fig. 5 (Color online) Instantaneous flow fields, for a LSC composed of a different number n of rolls[19]: (a) n = 1; (b) n = 2;(c) n = 3; (d) n = 4; (e) a snapshot illustrating a strong azimuthal motion, due to the elliptical instability. Parameters are Ra =5×106, Pr = 0.1, Γ = 1/5

最近，謝毅超等[12]設計了一種兩個同軸空心圓筒形成的圓環型的熱湍流系統（見圖6（a）），并在這種熱湍流系統中同樣發現了多湍流態現象。通過長時間的流場結構與傳熱效率的同步測量，發現系統的傳熱效率會在兩種穩定狀態下自發且隨機地轉換，見圖6（d），而且這種傳熱效率的轉換與流場結構的轉換一一對應。這種一一對應的關系表明，對稱性更高的四極子流動狀態（見圖6（c））有著更高的傳熱效率，而對稱性相對較低的偶極子流動狀態（見圖6（b））的傳熱效率也相對較低。通過這個實驗，他們認為在熱湍流系統中存在通過全局分叉實現的流動狀態自發且隨機地轉換，并且整個系統中的流動狀態由于自發的對稱破缺使得系統整體流動變得更加混亂。

圖6 (a) 謝毅超等設計的一種圓環型熱湍流系統的示意圖；(b) 偶極子流動狀態示意圖；(c) 四極子流動狀態示意圖；(d) Ra = 9.84×108時，系統傳熱效率Nu的時間序列.圖取自參考文獻[12]，圖中箭頭代表一一對應關系Fig. 6 (Color online) (a) Schematic of the annular convection cell. Sketches of (b) dipole state and (c) quadrupole state. (d) Time series of Nu at Ra = 9.84×108. The figure is adapted from Ref.[12].The arrows represent the one-to-one correspondences between the flow states and Nu

此外，徐翱和陳鑫等[20]最近在圓盤形熱湍流系統中也發現多湍流態的存在。我們發現在該種熱湍流系統中，除了已知的呈現為大尺度環流的流動狀態之外，還存在著一種混亂無序的流動狀態，此時，羽流不會沿著邊壁上升（下降），而會隨機地發射，大量的羽流選擇經過系統的中心區域抵達對面邊界，無法自組織形成大尺度環流。通過定量地分析系統處于不同流動狀態時的傳熱效率，我們同樣發現這兩種流動狀態的傳熱效率有著明顯的區別，如圖7所示，處于混亂無序的流動狀態時，根據Pr的不同，系統的傳熱效率相較于處于大尺度環流狀態時最高可提升8%。

圖7 在不同的Pr下Nuchao/Nucir - 1隨Ra數的變化[20]，這里的Nuchao和Nucir分別為流動處于混亂無序的流動狀態以及處于大尺度環流時熱輸運效率Nu的條件平均Fig. 7 (Color online) Values of Nuchao/Nucir - 1 as function of Ra for various Pr[20]. Here, Nuchao, Nucir are the conditional average Nu when the flow is in the chaotic state and the circulation states respectively. The figure is adapted from Ref.[20]

實際上，還有一類特殊的多湍流態現象，即熱湍流系統中大尺度環流的流向反轉現象[38,41]。在熱湍流系統中，正如我們在前文中一直提到的，一個重要的湍流結構是與系統尺寸相若的大尺度環流。大尺度環流的流動方向可以沿著順時針方向，也可以沿著逆時針方向。在流動過程中，順時針、逆時針方向運動的大尺度環流可以自發且隨機地切換，經過長時間的統計測量，這兩種流動狀態出現的概率幾乎相同。流向反轉一向是流體力學中極為重要的一類問題，同時也是一類小概率（極端）流動事件，一直吸引著眾多研究者的目光。但需要指出的是，對于大尺度環流流動方向的反轉是否也會帶來某些系統輸出參數例如熱輸運效率Nu顯著的變化，在目前的研究中并沒有發現這樣的特征。因此，我們將不把流動的反轉列入本文的討論范圍，不在這里進行過多的描述，感興趣的讀者可以參考筆者相關的論文[42]。

2 不同初始條件引發的多湍流態現象

我們接著討論不同初始條件引發的多湍流態現象。王啟等[13]在這個方面做了最為系統的探索。他們利用二維直接數值模擬，在1≤Pr≤100，107≤Ra≤1010的參數空間內，研究了在較大寬高比Γ（最高到32）二維矩形熱湍流系統中流動對于不同初始條件的響應。對于不同初始條件的給定，他們使用傅里葉模態基函數

來產生不同數量的對流渦結構，這里的n(i)表示在系統水平方向上排列的處于湍流狀態的對流渦的數量。此外，系統的初始溫度為具有隨機擾動的線性剖面，系統的初始速度則是根據當前控制參數下的雷諾數確定。

圖8給出了在Ra= 1010、Pr= 10、Γ= 8時，給定不同的初始條件（初始對流渦數量n(i)= 4～14，對應圖2中Γr(i)=Γ/n(i)= 2～4/7）系統中的流動狀態隨時間的演化。我們可以看出，對于六個不同的初始條件，經過長時間演化（數千個流動特征時間）后，系統最終演化出三種截然不同的湍流狀態，并表現出不同的系統熱輸運效率，如圖8（c）所示。對多湍流態形成的機理，王啟等利用橢圓形平面渦結構維持的條件即應變-渦量平衡關系并借助橢圓不穩定性理論中應變-渦量-渦的長寬比之間的定量關系[40]成功地預測了不同的湍流態在控制參數空間上的分布規律。

圖8 在Ra = 1010，Pr = 10，Γ = 8時，不同初始條件（對流渦的數目不同）下流動隨時間的演化[13]：(a) 雷諾數比值Rez/Rex隨時間的演化，這里R ez=H/v ，R ex=H/v，w、u分別為系統中沿z方向、x方向的速度；(b) Nu隨時間的演化；(c) 該控制參數下最終可以穩定存在的三種湍流狀態所對應的瞬時溫度場以及其對應的NuFig. 8 (Color online) Time evolution of (a) Rez/Rex and (b) Nu for different initial roll states, Ra = 1010, Pr = 10, Γ = 8[13]. Here,Rez=H/v, R ex=H/v, and w, u are the vertical and horizontal velocity respectively, (c) snapshots of the temperature fields for the three statistically stable turbulent states for different Nu numbers. The figure is adapted from Ref.[13]

王啟等[11]還利用二維直接數值模擬研究了寬高比以及熱湍流系統的傾角（溫度梯度的方向與重力方向之間的夾角）對于多湍流態存在與否的影響。他們發現，在寬高比為2的矩形熱湍流系統中，當系統保持水平時，系統中的流動是在水平方向上排列的雙環模態。當系統存在傾斜，傾角為9°時，由于浮力的作用，系統內的流動為單環模態。如果以此時的單環模態作為初值，連續地減小系統的傾角至系統水平，他們發現單環模態在系統水平時仍然可以穩定存在。另外，他們還指出在系統保持水平且在相同的控制參數下，雙環模態下的Nu比單環模態下的Nu大13%。進一步的研究發現，這種多湍流態現象在更大的寬高比下也同樣存在，并且不同的湍流態表現出不同的熱輸運效率。這個現象與Huisman等[21]在泰勒-庫埃特湍流系統中發現的多湍流態一致。

3 結論與展望

以上我們詳細討論了關于瑞利-伯納德熱湍流系統中的多湍流態現象研究的最新進展。多湍流態在熱湍流系統中以兩種形式呈現，一類則是流動在發展過程中自發產生并且自由切換的多湍流態，另一類是由于流動初始條件不同而產生的多湍流態現象。兩類多湍流態的研究中均發現當系統處于不同湍流態時，系統整體的熱輸運效率也相應改變，這也為之后探索相應的湍流調控方法提供了理論支持。下面，筆者就多湍流態的相關問題進行討論并給出展望。

在實驗室中進行湍流的研究是為了更好地理解自然界中、工程實際中的湍流問題，然而這些真實的湍流問題往往伴隨著極高的系統控制參數，如Re、Ra等。因此能否將實驗室中研究的成果順利地推廣至這些實際問題中要求我們對于流動處于何種流動狀態、是否還存在不同的流動狀態等等這些問題有清晰的認知。經典的湍流理論中認為，對于湍流流動，流動中大量的自由度被激發且湍流脈動足夠大，以至于所有的高維空間都被遍歷，此時流動的小尺度統計特性不再受到流動邊界或者外界的影響，然而這是否意味著大尺度流動狀態（結構）同樣只能存在唯一的一種流動狀態呢？對于這個問題，從本文綜述的內容角度來看，應該不是唯一的。

此外，20世紀中期，Kolmogorov及其學派[43]開始將湍流狀態下的流動視作類似于統計學角度的隨機場。換句話說，每一個真實的流場都被考慮成是“所有可能的場的統計集合”中抽取的一個“樣本”。時至今日，這種對于湍流場的處理已被大家廣為接受。任何變量的平均化都可以理解為相對于相應統計集合的概率平均化，這樣的處理一個最根本的前提在于各態遍歷假設。各態遍歷假設是統計研究的基石，其保證了我們在有限時間、有限空間、有限實現下得到的統計結果可以無限接近于理論的、真實的、期望的數值。在湍流理論中，認為當平均的范圍（時間、空間或者事件）足夠大時，對于該范圍上的均值將會趨同于統計概率的均值。正是因為這樣的一個假設存在，經典的湍流理論普遍認為湍流流動在給定某個初始條件以及邊界條件下應該僅僅存在一種流動狀態，與之對應的也僅僅存在一種系統輸出參數。此時，我們來回顧上文中綜述的兩類多湍流態現象，對于第二類多湍流態現象，部分觀點認為其與上述的統計學概念是自洽的，即在某一初始條件或者邊界條件下是一種確定的流動，有著確定的系統輸出參數；但是，也有部分學者認為各態遍歷假設已然要求湍流系統遍歷相空間中的任意狀態點，從某種意義上來講，系統應很快忘記初始狀態的信息，系統最終所處的狀態也應該與初始狀態無關。對于這一方面的討論，本文作者更傾向于認為第二類多湍流態現象是與各態遍歷假設是相符的。然而對于第一類多湍流態現象，筆者則認為其與Kolmogorov的理論不一致。在該類多湍流態現象中，一個明顯的特征是不同的湍流態對應著不同的系統輸出參數，這便會帶來一個問題，如何來定義上文中所說的足夠大的平均范圍呢？如果平均范圍（時間段）內流動未發生轉變，此時得到的系統的平均輸出參數會是該湍流態對應的系統輸出參數；而如果在平均范圍（時間段）內流動發生了轉變，此時的系統的平均輸出參數會受到不同湍流態所對應的不同系統輸出參數的影響。那么我們如何通過有限時間、有限空間、有限實現的實驗、數值模擬得到趨同于真值的結果呢? 因此，需要我們進一步的探索如何解釋這類自發的、隨機的湍流態之間的轉換。

另外，從N-S方程的角度出發，其作為一類極其復雜的非線性系統，多解現象以及多解之間的相互轉換又是普遍且可預期的。關于多湍流態的真實存在與否以及其產生的機理還有待進一步深入的研究，然而這并不妨礙筆者對多湍流態現象進行展望。

1） 目前眾多的關于多湍流態的研究大都集中于封閉的湍流系統。封閉湍流系統具有幾個突出的優點：第一，作為一個封閉系統，其整體響應參數和湍流內部能量耗散率有著精確的對應關系；第二，作為一個統計上的穩態系統，可以進行長時間測量來提高被測量參數的統計特性，例如可以精確地測量系統的整體熱傳輸效率、系統的外加阻力等。然而，封閉湍流系統也存在著尺度效應的問題。因此，使用封閉湍流系統來研究多湍流態問題也極大地限制了對這個問題的理解。那么，在非封閉的湍流系統如壁湍流中是否同樣存在類似的多湍流態現象？

2） 對于熱湍流系統中多湍流態現象的產生，Zwirner等[19]和王啟等[13]將目光鎖定在了橢圓不穩定性；郗恒東等[44]則認為高階的流動狀態參與其中。第一類多湍流態現象中不同的湍流態為什么會自發形成？什么因素促使不同的湍流態自發的轉換？如果可以解答這一問題將極大地提升對于湍流問題的理解。

3） 另一個疑問是通過給定不同的初始條件引起的第二類多湍流態現象是否會在長時間演化后同樣出現自發地、向不同的湍流狀態切換，兩類多湍流態現象是否從根源上來說是一致的，這也需要將來進一步的研究。

4） 湍流是否存在對大尺度湍流結構的選擇性？如何主動選擇流動的狀態進而調控湍流系統的輸運特性?

5） 針對第二類多湍流態現象，現有少量的研究結果主要集中于直接數值模擬的研究，缺乏相關實驗的證實。當然，不同初始條件的給定在實驗中存在一定的挑戰，這也需要進一步的探索。

實際上還有大量的問題值得進一步的探索，筆者希望通過本篇文章向更多的湍流研究工作者介紹相關的最新研究進展，一同推進理解相關的湍流問題。