側壁效應對Rayleigh-Bénard對流影響的數值模擬研究

劉苗苗，王 啟，萬振華，孫德軍

(中國科學技術大學 近代力學系，合肥 230027)

0 引 言

由溫差導致的熱對流現象廣泛存在于自然界和各種工程應用中，比如熱對流在海洋對流、大氣環流、地幔對流、太陽對流等自然現象以及在電子設備的冷卻和凝固過程、核反應堆設計、晶體生長等工程應用中扮演著重要角色。Rayleigh-Bénard（RB）對流模型是研究熱對流問題的經典物理模型之一，RB對流指流體層中下壁面加熱、上壁面冷卻導致的流動現象。該系統的控制參數主要是瑞利數Ra和普朗特數Pr，響應參數為努塞爾數Nu和雷諾數Re。當Ra較小時，流動由羽流主導，大尺度環流并不明顯[1]；隨著Ra的增加，系統逐漸進入湍流狀態，此時上下壁面存在很薄的溫度邊界層，冷熱羽流在溫度邊界層內生成并在浮力的作用下運動并自組織形成大尺度環流。隨著流動復雜性的增加，對RB對流研究的重心也轉為對湍流狀態下系統各物理量統計特性的研究[2-4]。

在RB對流的研究中通常使用側壁絕熱的溫度邊界條件，在側壁絕熱的充分發展的RB湍流中，體區的溫度近似均勻，因此側壁的溫度在大部分區域近似為上下壁面溫度的平均值。實際的對流換熱裝置中，側壁的導熱性往往不能忽略[5-9]。極端條件下，當側壁導熱系數相比流體很大時，可以認為側壁是理想導熱壁面，此時側壁的溫度為線性分布[10-22]。

前 人 在 寬 度∶深 度∶高 度 之 比 為6∶2∶1[23]和6∶4∶1[24]的三維方腔內研究了低Ra下不同側壁溫度對系統流動結構的影響。Corcione[25]在二維腔體研究了側壁溫度等于底壁溫度對流動和傳熱的影響。Stevens等[6]研究了圓筒中不同側壁溫度對Nu的影響。Moon等[26]研究了側壁溫度等于上壁面溫度的立方腔體內的流動。Vasu等[27]研究了三維方腔中側壁等溫條件或等熱流條件對流動模態的影響。也有研究討論了壁面厚度、導熱率對RB對流的影響，提出了側壁修正模型并進行了分析[6-8,25,28-36]。工程應用中熱對流的溫度邊界條件各種各樣，Pandey等[37]對方腔溫度邊界條件方面的研究進行了詳細的總結，指出側壁溫度邊界條件主要分為絕熱、加熱、冷卻、溫度線性分布四種。目前，對側壁等溫且溫度為上下壁面溫度平均值的對流問題研究仍然不多。

本文使用直接數值模擬（DNS）研究了Pr=5.3，寬高比 Γ=1的二維方腔和三維方腔內的RB對流。主要研究側壁等溫且溫度為上下壁面平均溫度的系統（ISO算例），并與側壁絕熱的經典RB流動（RB算例）進行對比。在二維方腔中，研究發現，Ra比較小時上下壁面Nu不相等，這與系統中出現的大尺度羽流在中心區域擺動的流動結構有關；而在三維方腔中，也發現了上下壁面Nu不相等的現象。文中也討論了側壁等溫條件對系統的熱量輸運（Nu）和動量輸運（Re）的影響。

1 控制方程和數值方法

腔體的高度為， 寬度為，寬高比固定為1，三維腔體深度為， 且寬高比同樣固定為1。上壁面溫度為、 下壁面溫度為。在Oberbeck-Boussinesq近似下，對流介質的物性參數認為是常數，僅在浮力項中考慮密度變化且其中為下的密度和熱膨脹系數。笛卡爾坐標系中無量綱化的不可壓縮Navier-Stokes方程為：

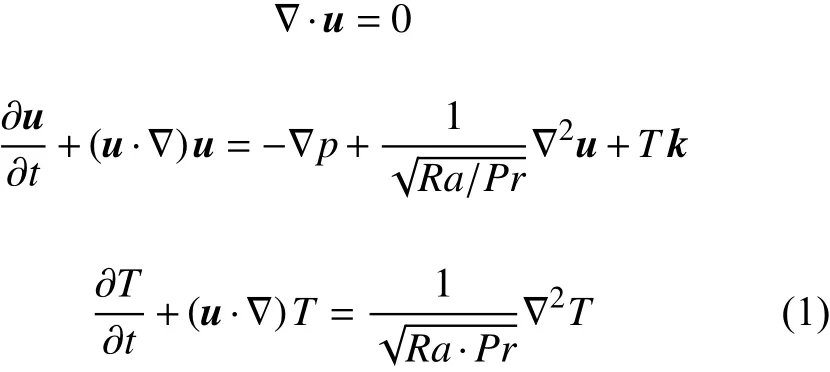
其中，u為 無量綱速度矢量；t為 時間；p為 壓力，T為無量綱溫度；k為豎直方向單位矢量；Pr=為普朗特數，表征了流體的動量擴散速度與熱擴散速度間的比值；無量綱參數為瑞利數，刻畫了溫差驅動湍流流動的強度，其中為重力加速度，為上下壁面的溫度差值，為運動學黏性系數，為熱擴散系數。無量綱化選取自由落體速度作為參考速度，腔體高度作為參考長度，參考時間為，溫度通過進行無量綱化。在各個固壁施加無滑移和無穿透的速度邊界條件。

數值求解使用課題組自主開發的lMn2d和lMn3d程序。該程序采用交錯網格，將矢量放置在網格界面上，將標量放在網格中心處，避免了速度和壓力解耦。空間離散使用二階精度的中心差分，對非線性項采用Adams-Bashforth格式，對黏性項和擴散項采用Crank-Nicolson格式。壁面附近采用拉伸網格以更好地分辨邊界層。在二維方腔和三維方腔內分別在1×106≤Ra≤1×1010、1×105≤Ra≤1×108范圍內計算了34個、20個算例。表1和表2給出了二維和三維計算采用的網格數。

表1 不同Ra下二維數值模擬的網格數Table 1 Grid resolutions for two-dimensional simulations with different Ra

表2 不同Ra下三維數值模擬的網格數Table 2 Grid resolutions for three-dimensional simulations with different Ra

2 結果與討論

2.1 方腔中側壁等溫對Nu數的影響

熱量輸運規律是熱對流系統中關注的重要問題。無量綱數Nu表征了對流傳熱的效率，其計算公式為：

其中，是單位面積的平板傳遞給對流介質的實際熱量，是熱傳導狀態下的熱通量，為熱傳導系數。為 對流導致的熱通量和傳導導致的熱通量之和，即：

則公式（2）可寫為：

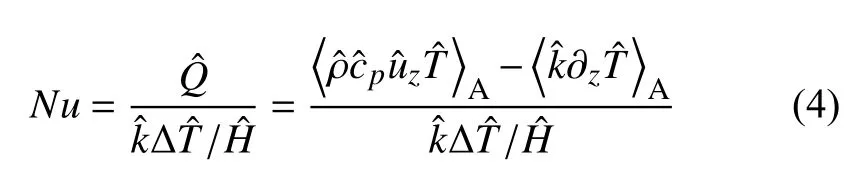
圖1給出了二維和三維方腔各個壁面Nu、|Nub/Nut?1|以 及各個側壁Nu與Nut的比值隨Ra的變化情況。從圖1（a、e）中發現Nub>NuRB而且Nut>NuRB，說明在二維和三維方腔中側壁等溫邊界條件增強了系統的傳熱效率。而且發現隨著Ra的增加，Nub、Nut和NuRB之間的差別逐漸減小。這是因為當側壁溫度為上下壁面平均溫度時，一部分熱量可以直接通過側壁來傳遞，從而繞開溫度邊界層，這個過程增強了系統的傳熱效率。而隨著Ra的增加，溫度邊界層的厚度急劇減小，導致側壁與溫度邊界層之間的傳熱減弱，這使得兩個系統的Nu逐漸相等。

當側壁溫度固定為上下壁面溫度的平均值時，由于系統存在的上下對稱性，直覺告訴我們上下壁面的Nu應該相等，然而有意思的是，從圖1（a、e）可以看出二維和三維方腔中上下壁面的Nu在某些比較低的Ra區間都出現了明顯的偏差，即Nub≠Nut，這說明系統的上下對稱性被打破，系統的流動結構可能發生了變化。

圖1（b、f）分別給出了二維方腔和三維方腔中Nub和Nut之間相對誤差隨Ra的變化。在二維方腔中發 現 |Nub/Nut?1|在Ra=1×106時 最 大，并 且 隨著Ra的增加不斷減小，當Ra≥1×107時|Nub/Nut?1|<0.5%，誤差可以忽略不計。在三維方腔中，上下壁面Nu不相等情形發生在有限的Ra區間內。從圖1（c、d）可以看出，在二維方腔中，當上下Nu發生較大偏差時，左右側壁Nu絕對值、側壁Nu與Nut比值的絕對值較大，而且側壁Nu正負相同。從圖1（g、h）可知在三維方腔中，當Ra很小，比如Ra=1×105時 ，側壁Nu絕對值、側壁Nu與Nut比值的絕對值較大，而且存在兩對側壁Nu互為相反數，導致側壁Nu之和為0，最終Nub=Nut；隨著Ra的增加，當Ra=7×105和Ra=1×106時，側壁Nu絕對值仍然較大，但是不再互為相反數，側壁Nu之和不為0，而且側壁Nu與Nut比值的絕對值較大，從而導致Nub≠Nut；隨著Ra進一步增加，側壁Nu絕對值迅速減小，與Nut的比值的絕對值也迅速減小，使得上下壁面Nu恢復相等。

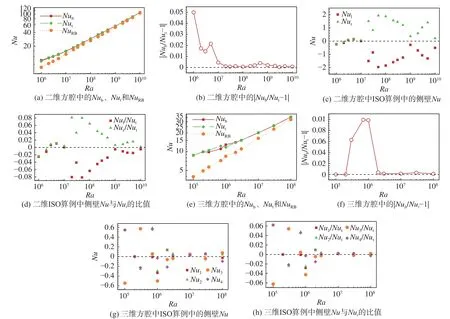
圖1 二維和三維方腔中各Nu隨Ra的變化以及Nu之間關系隨Ra的變化Fig. 1 Nu numbers and the relationships between them as functions of Ra in two- and three-dimensional square cavities

2.2 方腔中側壁等溫邊界條件對時均流場的影響

時間平均的流場可以反映系統的整體流動特性。為了探究圖1中上下壁面時均Nu不相等的原因，在二維方腔中選取Ra=1×106和Ra=2×107兩個典型算例討論了時均溫度場以及側壁Nu局部分布，在三維方腔中選取Ra=1×105、Ra=3×105和Ra=1×106三個典型算例研究了水平截面上的豎直速度分布。

Ra=1×106

圖2給出了二維方腔中 時ISO系統和RB系統的時均溫度場和速度場，以及ISO系統時均流場左右側壁的局部Nu分布。通過圖2可以觀察到，ISO系統和RB系統的時均場的共同特點是，它們均呈現出四渦模態。然而ISO系統流場上下出現不對稱，而經典RB系統的時均流場則呈現出完美的對稱四渦結構。由圖2（c）可知，ISO系統時均流場左側壁局部Nu(NuLl) 和右側壁局部Nu(NuLr)分布完全重合，但是NuLl和NuLr上下不對稱，進行積分后在左右側壁處得到Nul<0且Nur<0。系統存在能量的守恒，即Nub?Nut+Nul+Nur=0 ，最終導致Nub≠Nut。

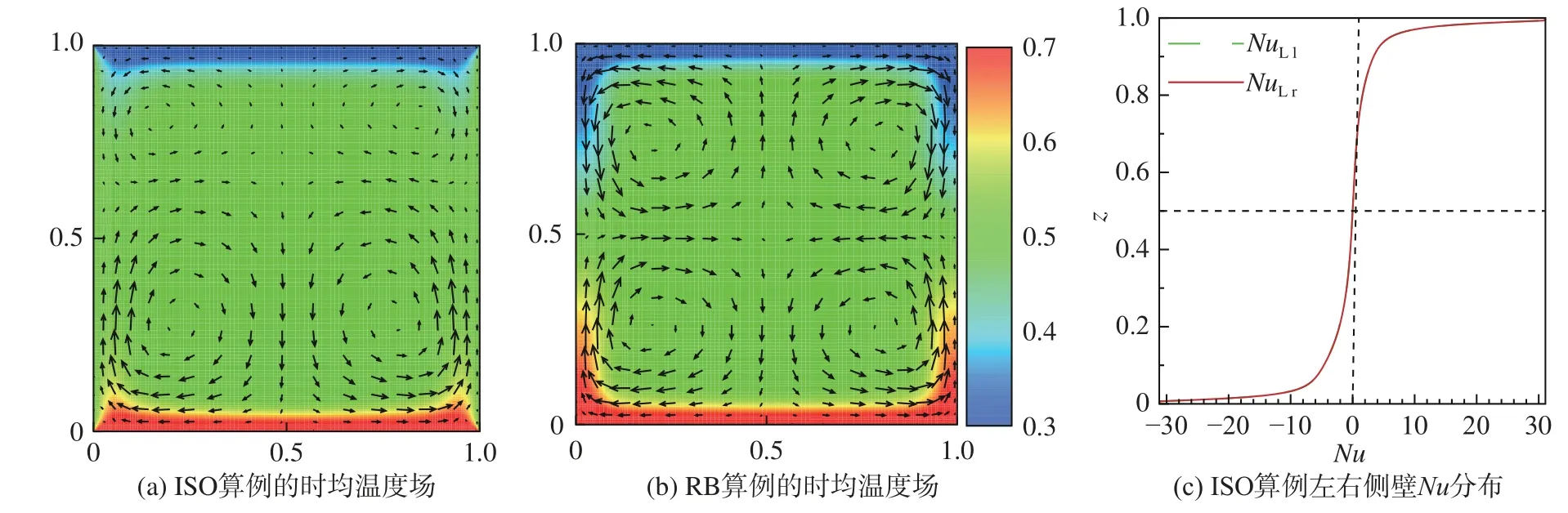
圖2 二維數值模擬中R a=1×106時的時均溫度場分析（圖中黑色箭頭代表速度矢量）Fig. 2 Analysis of time-averaged temperature field when R a=1×106 in two-dimensional simulation(Black arrows represent velocity vectors)

圖3展示了Ra=2×107時ISO系統和經典RB系統的時均流場以及ISO系統時均流場的左右側壁Nu分布。在計算過程中，兩類系統都沒有發生大尺度結構的流動反轉。通過圖3（a、b）可以發現兩個系統均存在一個大的環流結構，且在對角線上存在一對角渦。圖3（c）中左右側壁局部Nu呈現出反對稱分布，即NuLl(z)=?NuLr(1?z)， 最終積分得到Nul=?Nur，側壁整體傳熱為0。由于系統能量平衡，所以上、下壁面的Nu必然相等。

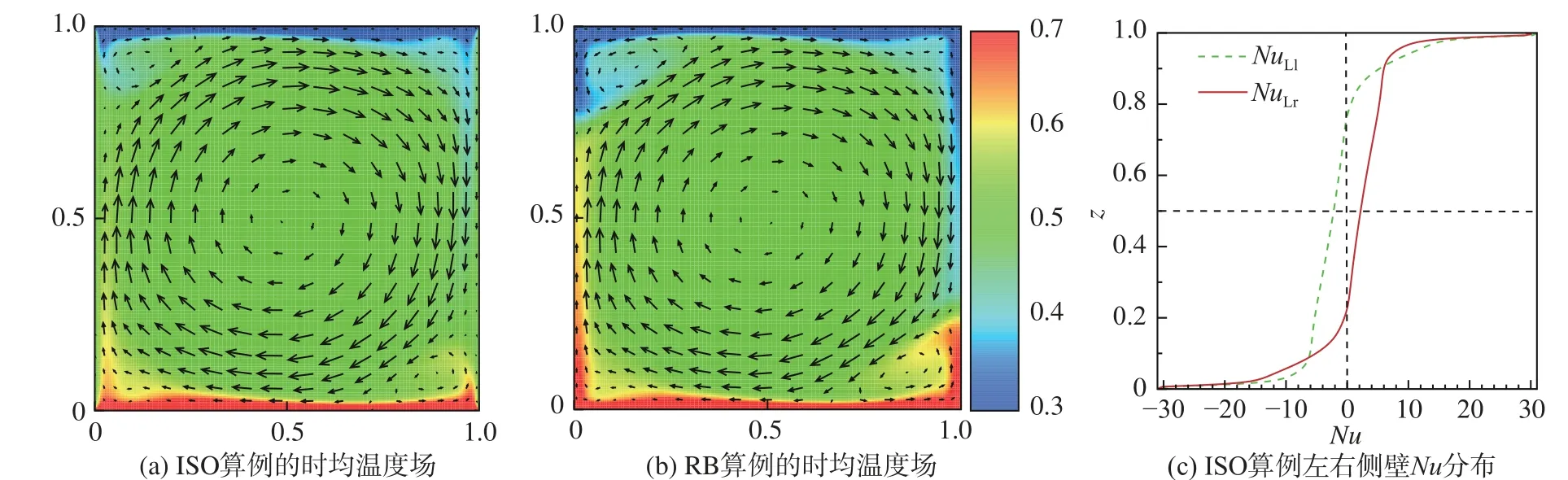
圖3 二維數值模擬中R a=2×107 時的時均溫度場分析Fig. 3 Analysis of time-averaged temperature field when R a=2×107 in two-dimensional simulation

圖4展示了三維RB算例和ISO算例在計算的Ra區間內定常、非定常的流動狀態相圖。可以發現上下壁面Nu的不相等情形主要發生在側壁等溫系統剛剛由定常轉為非定常流動的區間內。

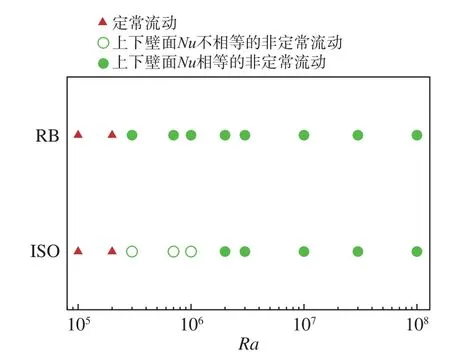
圖4 三維方腔內RB對流的流動狀態相圖Fig. 4 Phase diagram of flow states in three-dimensional RB convection

Pallares等[14]指出可以根據水平截面上豎直速度分布判斷系統內的流動結構。圖5是Ra=1×105、Ra=3×105、Ra=1×106時三維ISO算例的時均流場在z= 0.15、0.5、0.85處的豎直速度分布，可看出系統始終存在單渦模態。觀察圖5（a）中z= 0.5平面內的豎直速度分布，可以發現系統的定常上升流動和下降流動關于對角面對稱。隨著Ra增加，系統進入非定常流動狀態，圖5（b、c）中z= 0.5面上的豎直速度分布表明上升流和下降流之間失去了對稱性，該非對稱結構導致側壁整體的Nu之和不為0，從而上下壁面的Nu不再相等，這與前面提到的二維情形比較類似。隨著Ra進一步增加，側壁Nu迅速減小，相對于上下Nu可以忽略不計，此時上下壁面的Nu再次相等。

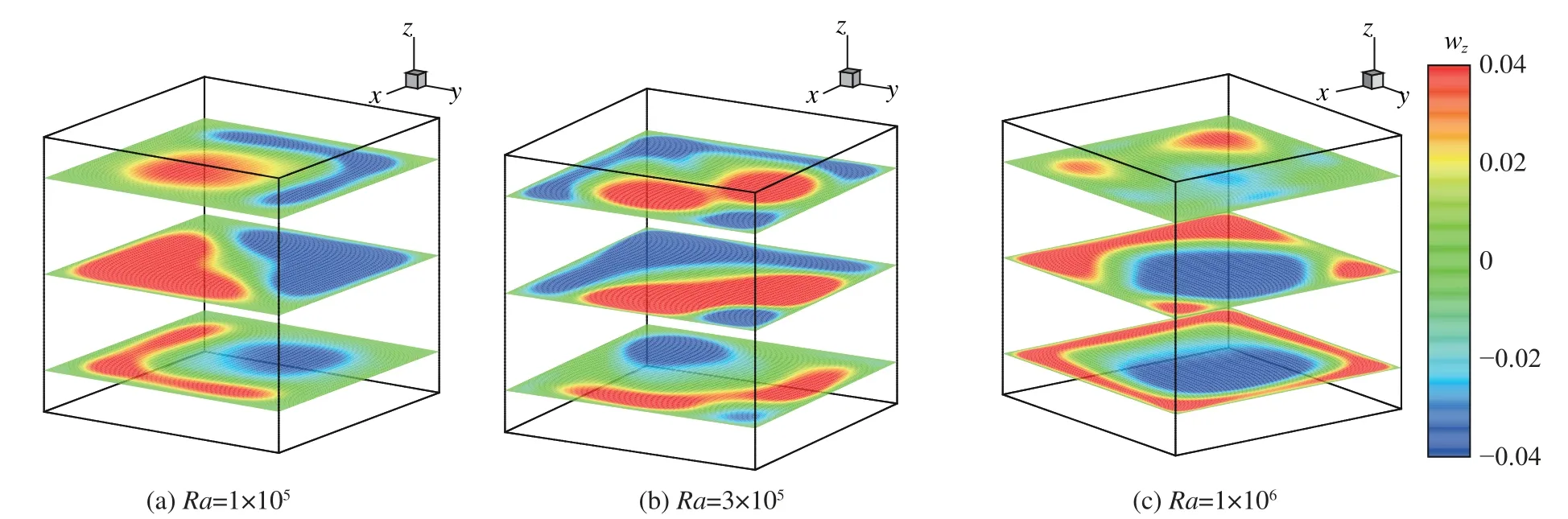
圖5 側壁等溫邊界條件的三維RB對流時均豎直方向速度場在水平截面高度為z = 0.15，z = 0.5和z = 0.85處的分布Fig. 5 Time-avraged vertical velocity for the three-dimensional RB convection with isothermal sidewalls at z = 0.15, 0.5, 0.85

2.3 腔側壁等溫對Re的影響

雷諾數是熱對流系統另一個重要的響應參數，可以用于刻畫湍流的強度，其計算公式為：

我們分別使用ReISO和ReRB分別表示ISO系統和經典RB系統的Re，探究側壁等溫邊界條件對Re的影響。圖6給出了二維和三維方腔流動中ReISO、ReRB和ReISO/ReRB隨Ra的變化。通過圖6（b、d）可以發現ReISO/ReRB<1幾乎在所有計算Ra值區間下成立，只在二維方腔中Ra=3×107時大于1，而且與1僅相差0.90%，說明側壁等溫一般會減小系統Re。

圖6 Re和R eISO/ReRB隨著Ra的變化Fig. 6 Re and R eISO/ReRB as functions of Ra

2.4 二維方腔中側壁等溫對瞬時流場結構的影響

本小節進一步討論上下壁面Nu出現不相等時對應的瞬時流動狀態。角動量的符號可以表征大尺度環流的瞬時流動方向，其計算公式為：

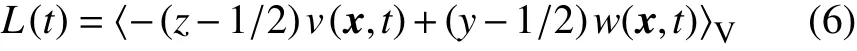
其中 (v,w)是 速度矢量的分量，表示對整個計算區域進行平均。

Ra=1×106

圖7展示了 時二維ISO系統和RB系統的角動量變化以及典型的瞬時溫度場。如圖7（a）所示，可以看到經典RB對流系統的角動量隨時間發生頻繁的正負變化，說明系統在連續不斷的發生流動反轉。圖7（b、c、d）展示了經典RB對流系統發生反轉的連續過程，可以觀察到此時流動由羽流主導，瞬時流場中存在大渦結構，隨著角渦的增長并發生融合，大尺度環流發生反轉。圖7（e）給出了這個反轉過程中角動量的變化。圖7（f）展示了ISO系統的角動量變化，發現角動量同樣頻繁發生正負變化，但是在瞬時溫度場中沒有發現大尺度環流結構以及流動反轉，此時流動也由羽流主導，沒有形成明顯的大尺度環流，而是出現如圖7（g～i）所示的三種典型的瞬時溫度場，分別為大尺度熱羽流占據中心區域并進行擺動的流場、大尺度冷羽流占據腔體中心區域并進行擺動的流場和冷熱羽流無序發射的流場。

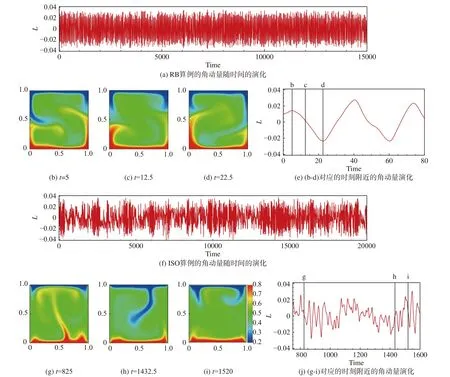
圖7 二維計算中R a=1×106時RB算例和ISO算例的角動量隨時間的演化以及典型瞬時溫度場，其中（b～d）為RB算例發生反轉時不同時刻的瞬時流場，（g～i）為ISO算例三個不同時刻的典型瞬時溫度場Fig. 7 Evolution of the angular momentum and typical instantaneous temperature fields for the adiabatic-sidewall case and the isothermal-sidewall case with R a=1×106 in 2D simulations. Figs. (b～d) instantaneous temperature fields during a flow reversal process for the adiabatic-sidewall case. Figs. (g～i) three typical instantaneous temperature fields for the isothermal-sidewall case

當系統處于大尺度熱羽流占據中心區域并進行擺動的流動結構時，下壁面Nu小于上壁面Nu；當系統處于大尺度冷羽流占據中心區域并進行擺動的流動結構時，上壁面Nu小于下壁面Nu；當系統處于冷熱羽流無序發射的流場結構時，上下壁面Nu幾乎相等。由于三種流動結構持續的時間不同，導致了時均Nu和時均流場的不對稱。而隨著Ra的逐漸增加，系統流動加強，瞬時流場呈現出穩定的大渦結構，上述三種結構消失，此時上下壁面的Nu相等。

3 結 論

本文結合二維和三維直接數值模擬方法研究了側壁恒溫且溫度為上下壁面平均值的邊界條件對RB對流的影響，并與傳統的側壁絕熱條件下的RB對流進行了比較。寬高比 Γ固定為1，普朗特數固定為Pr= 5.3，二維和三維研究的Ra區間分別為1×106≤Ra≤1×1010、1 ×105≤Ra≤1×108。主要結論歸結如下：

1）Ra較小時，在特定Ra區間內存在上下壁面Nu不相等的現象。該現象出現時，流場結構存在明顯的上下不對稱，導致側壁的Nu之和并不為0，從而上下壁面的Nu不相等。隨著Ra的增加，側壁的Nu減小且可以忽略，此時上下壁面的Nu恢復成相等。

2）側壁恒溫時系統的傳熱效率要高于側壁絕熱情況，這是由于側壁恒溫條件下，一部分熱量可以直接通過側壁來傳遞，從而繞開溫度邊界層。

3）當采用恒溫邊界條件時，系統的Re要小于側壁絕熱條件下對應的Re，從而表明側壁恒溫邊界條件會降低系統的流動強度。