基于改進層次分析法的企業金融風險分析模型*

謝亞妮

（榆林學院管理學院 榆林 719000）

1 引言

企業在從事各類金融活動時，所發生的利率、匯率以及商品價格等方面的損失均稱為金融風險，但是不同原因導致的損失結果存在差異，其風險程度則存在差異。企業在運營管理過程中，準確分析風險類型，對于降低金融損失具備重要意義［1～2］。層次分析法作為一種決策方法，以要實現的總目標為依據，將其實行分解處理形成數個目標后，依據各個因素之間的關聯［3］，構成多層次的分析結構模型，依據相應的定量和定性方法，獲取以最高層為參照的權值結果以及總目標的綜合權重，確定最佳方法，實現多目標的綜合分析和評價。當下，如何準確分析企業金融風險，已經成為學術界眾多學者關注研究的問題。陳振龍［4］等和張冰潔［5］等針對金融風險的分析，分別以藤Copula分組模型、CoES模型為基礎，度量金融風險水平，展開相關分析，分別依據企業資產之間的關聯性和損失均值的度量結果，分析企業風險水平。上述方法在度量分析過程中，對于權重指標的分析和確定存在一定欠缺，風險指標之間的關聯性無法清晰、準確體現。存在分析結果的片面性［6］。基于此，本文以層次分析法的風險指標權值確定為基礎，采用灰色關聯對其實行改進，確定指標間的關聯性，避免層次分析法的局限性，保證風險指標權重的客觀性，實現企業金融風險的可靠分析。

2 改進層次分析法的企業金融風險分析模型

2.1 企業金融風險指標體系構建

企業金融風險分析時，需量化分析對企業金融風險造成影響的因素，即風險指標體系的構建。本文采用層次分析法建立企業金融風險分析指標體系，指標體系包含一級指標、二級指標，將上述指標用于企業金融風險分析。指標詳情見表1。

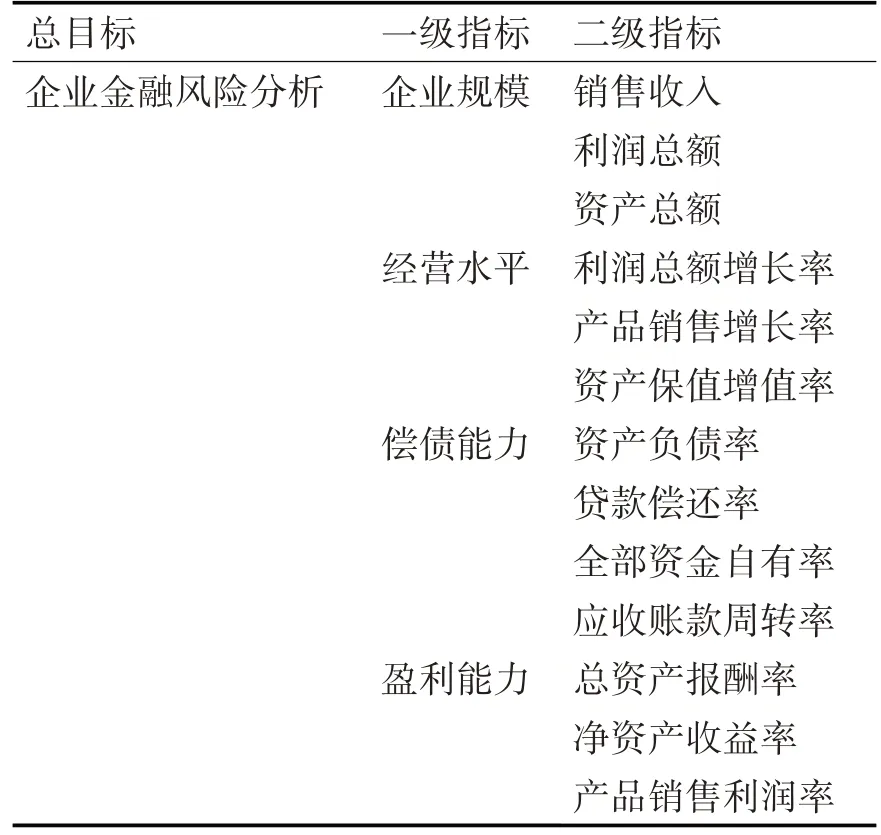
表1 企業金融風險指標體系

2.2 風險指標的模糊化處理

X=｛x1，x2，x3，x4｝表示企業風險分析論域，其中x1、x2、x3、x4分別表示四個一級風險指標，以分析對象來說，每一個風險指標對分析結果的貢獻均存在差異［7～8］，為實現指標的定量分析，需對其實行模糊化處理，處理采用隸屬度函數完成，保證樣本數據處于［0，1］范圍內。設置企業的信用等級用j表示，且j=1，2，3，4，分為4個等級，分別表示不信任、較低信任、一般信任和完全信任，見表2。

表2 等級詳情

信用等級集合為：Y=｛y1，y2，y3，y4｝，其中包含的元素分別對應4個等級；x1、x2、x3、x4的6個界限值為：ki=（i=1，2，3，4，5，6），則隸屬度函數的定義為

以上三個公式分別是j=1、j=2，3、以及j=4的條件下的隸屬度函數。

2.3 基于改進的層次分析法的指標權重確定

風險指標確定后，需確定指標的權重，為保證權重結果的客觀性［9］，本文將灰色關聯模型和層次分析法相結合，改進層次分析法，以此完成所有風險因素的整體對比機制［10］，并且通過灰色關聯系數矩陣確定各個專家對于風險總貢獻度的認知結果，結合灰色關聯和層次分析法的優勢，完成企業金融風險分析［11］。其詳細步驟如下所述：

1）m表示數量，包含專家和待分析序列，分析因素數量用n表示，對風險因素實行打分和處理，分別為層次和總體，處理標度為（0，1），該值大小決定風險程度；前者越大后者風險越小［12］。X0（k）表示標準參考序列，其為總體風險因素，為獲取待分析矩陣Xi（k），以列的方式將待分析風險實行排列得出，且i=1，2，…，m，k=1，2，…，n。

2）對排列后的Xi（k）和X0（k）進行處理，得到：

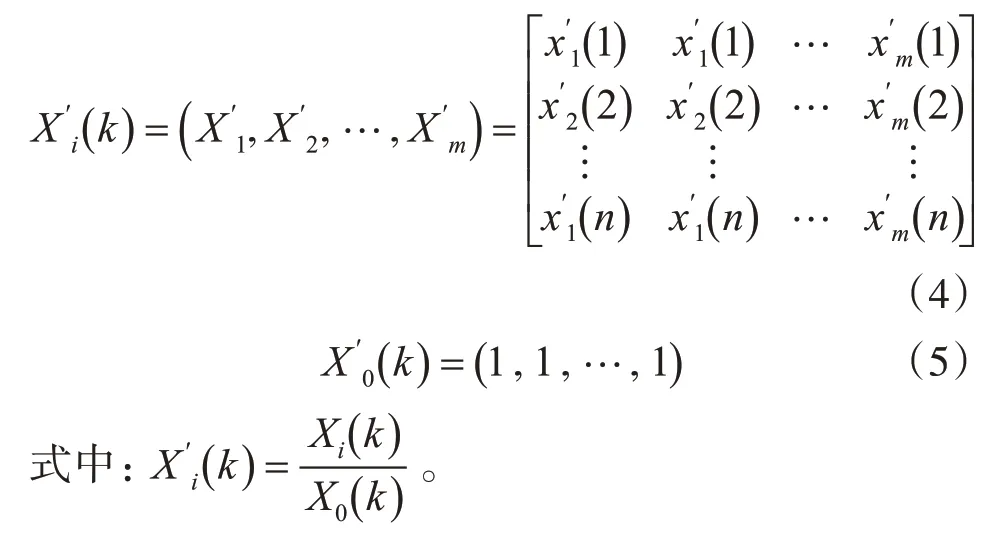
3）為獲取絕對差矩陣，采用絕對差，對初值化后的矩陣實行運算［13］，則得出：

式中：分辨系數用ζ表示，其取值最佳時，可控制分析結果的準確性，同時提高區分能力，僅為ri（k）；M、m表示最大、最小元素，屬于Δi(k)。對式（7）實行關聯運算后，獲取ri（k）矩陣。

5）為獲取互反判斷矩陣，對ri（k）實行拆分處理，將其內各個元素實行倍數增加，均為10倍，取整數結果，形成新矩陣以列的順序提取矩陣中的專家評分結果，使其形成縱橫對比形式，僅為風險因素；分別以行、列各自為參照元素［14］，相互對比獲取兩者差值，如果比較元素小于參照，差值結果加1。按照該處理方式，依據獲取順序，將獲取的結果組成互反矩陣，即為灰色關聯判斷矩陣Ai。

6）對Ai分別實行方根運算，并以上級風險為參照，獲取風險因素對其的影響權重［15］：

7）一致性檢驗：計算Ai特征值［16］，具體為

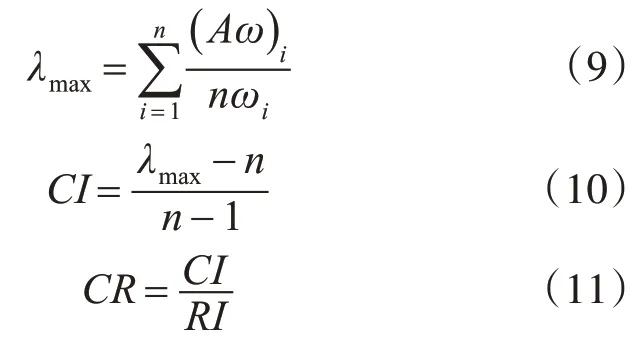
式中：C I、RI均表示一致性指標，后者為隨機；λmax表示特征值；C R表示一致性比率，依據該值結果判斷Ai是否符合一致性，其值小于0.1，表示符合，反之不符合。當其不符合時，為不影響風險分析結果，將其刪除；最后依據專家分析結果，確定每一個風險因素的權重，且以上級總風險為參照。

2.4 模糊綜合評價模型

依據Y=｛y1，y2，y3，y4｝等級完成各個風險指標的評價，對其實行量化后，建立模糊關系矩陣R：

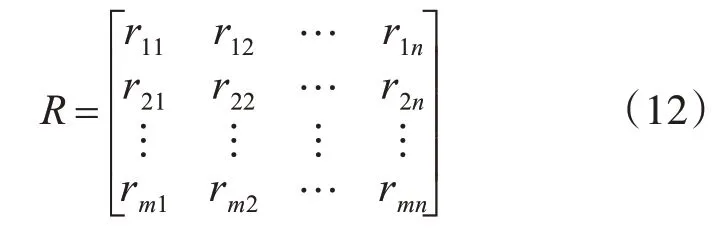
式中：rij表示隸屬度，屬于模糊子集，且在以xi為參照的情況下，yi的分析結果。

將獲取的權重向量集合和R權重向量集合ω={ω1，ω2，…，ωm}組合，得出：

3 實驗結果與分析

為驗證本文方法對于企業金融風險分析的應用效果，選取國內某知名生產企業連續5年內的實際財務數據作為測試使用數據。本文方法分析指標結果見表3，償債能力是對流動比率和速動比率實行擬合后獲取的數據。

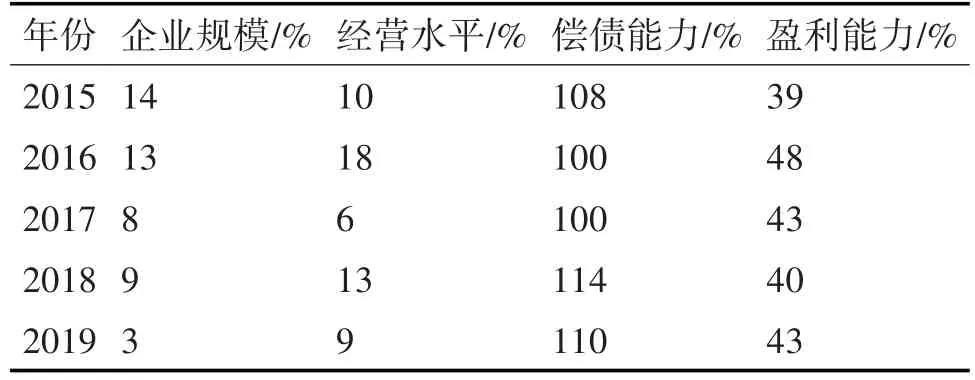
表3 指標數據結果

分析本文方法指標選取的準確性，對于分析結果存在直接影響，本文采用差異度作為衡量本指標，測試本文選取指標和基準指標間的差異度，結果見圖1。依據圖1測試結果可知：本文選取指標與基準指標吻合程度較高，因此，采用文本方法確定的指標可用于準確完成企業金融風險分析。

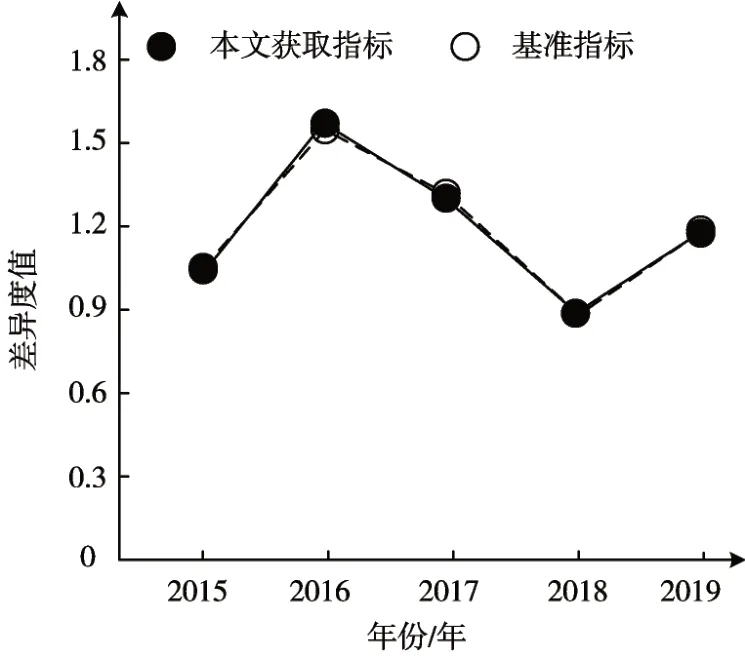
圖1 指標的差異度測試結果

由于每一個風險指標對分析結果的貢獻均存在差異，即不平衡現象，為實現指標的定量分析，需對其實行模糊化處理。因此，測試本文方法對指標的模糊化處理效果，采用F1-measure（加權調和平均值，為查準率和召回率）、G-mean（幾何平均值，為召回率和特異度）兩種指標作為衡量標準，分析本文方法的處理結果，見圖2。兩者值越接近1表示模糊化效果越好。依據圖2測試結果可知：本文方法在對不同年份中的風險指標實行模糊化處理的F1-measure和G-mean結果均在0.8以上，表明本文方法可有效處理風險指標對分析結果的貢獻均存在差異，即不平衡現象。

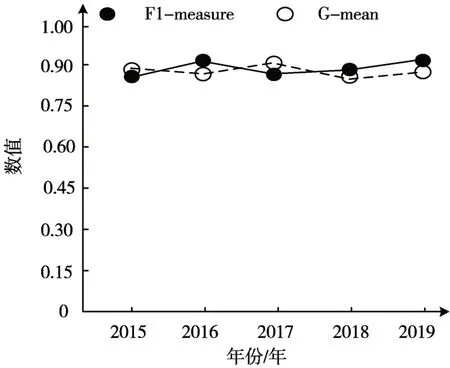
圖2 模糊化效果測試

分辨系數ζ值對于準確率和關聯系數的區分結果存在直接影響，因此，測試在其不同取值下的分析結果的準確率以及有效區分結果，見圖3。從圖3可知：ζ取值不同，其隨著指標間關聯系數的關聯程度增加，呈現不同變化，ζ=0.4時，本文方法分析結果的準確性呈現下降趨勢；取值為0.6時，本文方法分析準確率呈現上升趨勢；取值為0.5。時，則分析準確率平穩在0.90上下；除此之外，關聯程度高于50%以后，關聯系數的有效區分結果中，取值為0.5時，最高區分比例高于0.95，雖然在關聯程度低于50%以內時，區分比例在0.5左右，但是，結合實際運算過程中，指標間的關聯程度在模糊化處理后，關聯程度高于50%，因此，本文方法ζ=0.5。

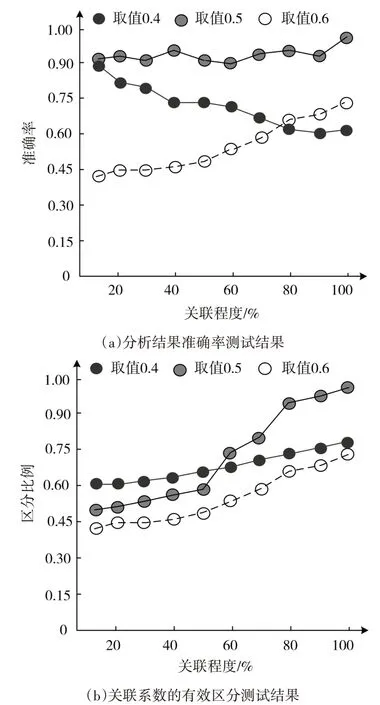
圖3 分辨系數測試結果

依據文中創建的指標體系，采用本文方法獲取判斷矩陣后，計算一級指標的權重結果，并獲取模糊關系矩陣，兩者結合后，計算實驗某知名生產企業金融風險評估結果為B=（0，0.39，0.52，0.40），依據最大隸屬度原則，確定B的最大分量為0.52，即為企業的風險對應等級為Y4，表示該企業的信用等級為完全信賴。依據該信用結果，對該企業5年內的交易分布結果實行統計，結果為5年的平均結果，見圖4。依據圖4測試結果可知：該企業83.5%的交易均分布在完全信賴的信用等級中，一般信賴的交易比例為12.6%，信賴較低的交易比例為3.2%，不信賴的交易分布僅占0.7%。該結果體現本文方法可有效完成企業的金融風險分析，并且可為企業交易分布的風險統計提供可靠依據，保證企業掌握自身交易分布情況，針對交易風險采取應對措施。

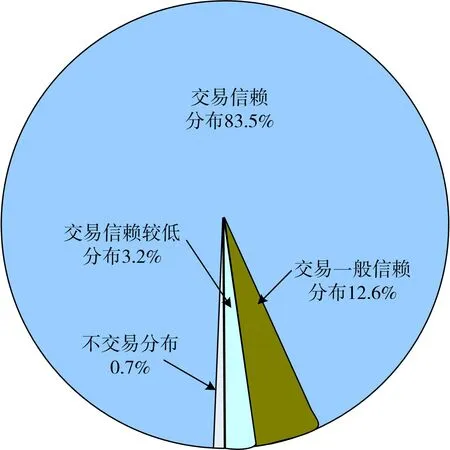
圖4 企業交易分布情況

4 結語

企業的金融狀態，決定企業的發展和正常運營，因此，為保證企業的良性運轉，需及時掌握企業的金融風險狀況。本文研究基于改進層次分析法的企業金融風險分析模型，對企業運行中的金融風險實行定量以及定性分析，判斷企業的信用等級。并通過相關測試表明：本文方法選取的風險指標的準確率較高，可用于表示企業的金融風險；可良好地處理金融風險指標中不平衡數據，保證企業的金融風險結果可靠性，并可依據分析結果統計企業的交易分布情況，有助于企業的金融管理。