基于改進型相似度的協同過濾算法的研究

吳錦昆，單劍鋒

(南京郵電大學 電子與光學工程學院、微電子學院，江蘇 南京 210023)

0 引 言

在大數據時代，每個個體在日常生活上網產生的一些行為，都會生成大量的數據。這些數據對于互聯網平臺來說是描述用戶的重要信息來源，再利用這些數據結合利用協同過濾算法，能夠促進互聯網平臺的高效運行。當人們處在面對大量的信息與平臺推送各種各樣的短信時，要從海量的信息中獲取有用的信息是困難的，面對海量的信息更是一個令人頭疼至極的問題。所以大數據被運用的場合越開越普遍，抖音、拼多多、淘寶等這些互聯網平臺都會根據用戶的歷史行為以及對產品的偏好，來對用戶進行個性化、精準化推薦，給用戶帶來更加良好的體驗。

不論是基于用戶還是基于物品的協同過濾算法，數據總是存在稀疏性的問題。文獻[1]中利用隨機性對原有的用戶-商品評分矩陣進行填充再進行矩陣變換，文獻[2]提出挖掘用戶的相關信息，文獻[3]提出利用BP神經網絡來預測用戶的評分，從而改進數據集稀疏性的問題。文獻[4]中考慮用戶的偏好以及物品的內在屬性從而改進相似度計算，改進了協同過濾算法相似計算。文獻[5]提出了一種融合型余弦相似度計算方法，其中包含了相似度修正參數和基于用戶屬性的特征向量，解決了用戶之間不同評價體系和用戶的不同屬性的問題。文獻[6]提出了一種全新的相似度計算方法，利用兩個用戶對相同物品的評價的比值作為相似度計算的依據，使提出的協同具有更高的精確度和較低的平均絕對誤差。文獻[7]利用項目的標簽及評級信息，引入了時間加權因子來解決數據的稀疏性的問題。文獻[8]根據不同用戶的評分范圍，將用戶分為正常、嚴格、寬裕和中間四種，提出了基于標準差比例的改進和統一的基線改進模型，以便消減經典基線估計模型的局限性。文獻[9]根據Translation-based模型在稀疏的數據集上的良好表現，將這種模型與遞歸神經網絡模型進行融合，提出了Recurrent Translation-based Network模型。文獻[10]采取隨機梯度下降法優化了矩陣分解，結合譜聚類方法填充方法，有效降低了數據的稀疏性對于準確性的影響。文獻[11]采用主成分分析法，對用戶-項目評分矩陣進行降維，再對K-means算法進行改進，提高了聚類的速度，有效提高了準確率和召回率。

1 協同過濾算法

現今，協同過濾算法大致分為三類：一類是基于用戶的協同過濾算法，一類是基于物品的協同過濾算法,還有一類是基于模型的協同過濾算法。

協同過濾算法被廣泛應用于人們日常生活的方方面面。例如音樂、電影、網購等。為了使用戶能夠更加迅速地瀏覽與自己偏好相關的音樂、視頻、商品，各個平臺都在尋找更加適合平臺的推薦算法，給用戶帶來極致的體驗。

協同過濾算法，主要功能是找出與某一用戶相似的用戶，將相似用戶的所評級或消費的商品推薦給這個用戶；或者根據用戶歷史消費過的商品，推薦給用戶相似的商品[12]。分別是基于用戶的協同過濾算法和基于物品的協同過濾算法。

1.1 相似度計算

在傳統的協同推薦算法中，計算相似度的方法主要有兩種：皮爾遜相似度、余弦相似度。該文主要針對協同過濾算法中的皮爾遜相似度計算進行改進。皮爾遜相似度計算公式如下：

(1)

余弦相似度類似于求兩個向量形成夾角的余弦值，根據用戶對電影的評分形成空間向量[13]，計算空間向量形成夾角的余弦值，確定不同用戶之間的相似度。

余弦相似度計算公式如下：

(2)

(3)

式中，I,U分別表示u1,u2評價過的項目的交集，對i1,i2評價過用戶的交集。相較于皮爾遜相似度，余弦相似度中沒有考慮到用戶評價的平均分，忽略了用戶自身帶有的評價體系。

1.2 協同過濾算法準確度的評價準則

準確度的評價指標，是衡量協同過濾算法準確度的一個重要方面。選取合適的評價指標能夠很好地衡量算法改進前后的效果。文獻[14]中，詳細闡述了推薦系統中的各種評價指標，從預測評分的準確度上有平均絕對誤差、均方根誤差，根據最終的平均絕對誤差值的大小，從而確定算法的優劣，得到的平均絕對值較小的協同過濾算法推薦的準確度較高。從分類的準確度上有準確率、召回率，還有一些其他評價指標，深入分析與比較各個指標之間的差異。該文采用平均絕對誤差(MAE)來衡量改進相似度計算后的推薦算法的性能。

1.2.1 平均絕對誤差

平均絕對誤差是最經典的計算真實評分與預測評分的差異。表達式如下:

(4)

1.2.2 均方根絕對誤差

均方根絕對誤差，是將絕對誤差求平方之后，再求平方根。表達式如下：

(5)

2 改進的相似度計算方法

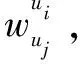
sim(u1,u2)=

(6)

(7)

皮爾遜相似度改進前與改進后的相似度計算結果比較：

在表1中，存在4個用戶，分別對四個物品都進行了評分，依據式(1)可以計算出用戶之間的皮爾遜相似度，計算結果如式(8)～式(11)所示。

(8)

(9)

(10)

(11)

用戶u1,u2，用戶u1,u3以及用戶u1,u4的相似度都為1，可以判斷出用戶u1,u2,u3,u4之間具有相同的相似度，但是從用戶u1,u2,u3,u4對電影的評分的不同可以看出他們之間的相似度應該有一定的差異，可以從表中的數據判斷出用戶u1,u2之間的相似度應該高于用戶u1,u3之間的相似度，用戶u1,u4之間的相似度應該高于用戶u1,u2和用戶u1,u3之間的相似度，而不是四者之間具有相同的相似度。

為了解決上述計算結果中用戶之間存在差異不明顯的問題，引進用戶差異因子來區分用戶，改進后的皮爾遜相似度計算過程如式(12)～式(15)所示。

(12)

(13)

(14)

(15)

用戶u1,u2之間的相似度為0.5，用戶u1,u3之間的相似度為0.4,用戶u1,u4之間的相似度大約為0.67,用戶u2,u3之間的相似度為0.8，可以看出改進后的相似度計算方式得出用戶u1,u2,u3,u4之間具有不同的相似度。經過改進后的皮爾遜相似度得到的計算結果表明，引入用戶差異因子改進的皮爾遜相似度計算方式，更加能夠體現出不同用戶之間的差異，能夠對之前相似性較高的用戶進行更加精細的區分。

表1 不同用戶對已購商品的評分

3 實驗步驟及結果分析

3.1 實驗步驟

仿真過程建立在Spyder平臺上基于Python3.8版本進行，主要建模仿真步驟如下：

(1)導入相關實驗相關的Movielens 1m相關數據集。每一次都將數據集按照7∶3的比例劃分為訓練集和測試集，經過三次得到不同的測試集與訓練集，部分數據集如表2 所示。

(2)構建用戶-項目評分矩陣，分別采用皮爾遜相似度與改進后的皮爾遜相似度計算公式，來計算用戶之間的相似度。

(3)根據計算得到的相似度，選擇鄰居個數，預測用戶對測試項目的評分。

(4)根據預測得到的評分計算MAE值。

表2 Movielen 1m部分數據集

在表2中UesrID代表用戶編號，MovieID代表電影編號，部分電影編號對應的電影如表3所示，ratings代表對應的用戶給對應電影的評分，timestamp代表時間戳，即用戶對電影評分的時間。

表3 部分電影編號與對應電影

續表3

3.2 實驗數據集介紹及數據集處理

該文采用的數據集來自Movielens數據集中的ml-1m數據集。目前主要的協同過濾算法基本上都采用Movielens類數據集。在ml-1m數據集中包含了3 952部電影，6 040個用戶，評分在1～5之間。將數據集劃分為訓練集和測試集，訓練集用來計算用戶之間的相似度,測試集用來根據訓練集計算出的相似度進行預測評分[13]。

3.3 實驗結果及分析

對于最近鄰數分別選取k=25、50、75、100，根據劃分不同的訓練集與測試集分別進行3次仿真實驗，對同一次劃分的訓練集和測試集，先用改進前的協同過濾算法進行仿真，然后用改進后的協同過濾算法對劃分好的數據集進行仿真，仿真后得到MAE值，然后再對三次得到的MAE值求平均值，以消除仿真得到的MAE值存在一定的偶然性誤差。經過仿真實驗得到不同的最近鄰數的結果分別如表4、表5所示。

表4 算法改進前MAE值

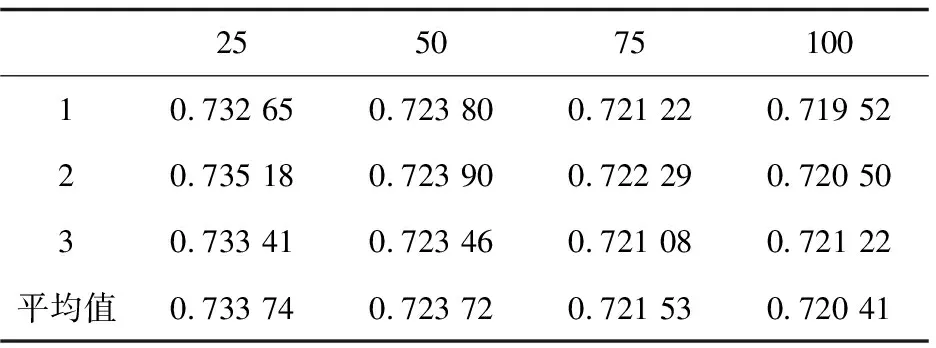
表5 算法改進后MAE值

根據表4、表5中的第四行中的平均值，得到的MAE平均誤差曲線如圖1所示。

從圖1中可以看出，改進后協同過濾算法的平均MAE值基本上都低于改進前的平均MAE值，在近鄰k值選取較小的值時，MAE值下降比較明顯，特別是在最近鄰數k選取50時，MAE值有較大的下降。在近鄰k取較大值，由于選取的近鄰k值較大，會降低協同過濾算法相似度計算的作用，導致MAE值并沒有明顯的下降。改進后的算法在最近鄰數k選取較大時，效果不夠明顯，也是未來算法改進的一個方向。

圖1 改進前后MAE值曲線

4 結束語

因為傳統的協同過濾推薦算法在皮爾遜相似度計算中只考慮用戶之間的線性關系和用戶的平均分，沒有考慮到每個用戶更加深層次的評價體系，用戶本身的評價體系會對用戶對商品的評分產生一定的影響，所以在利用皮爾遜相似度計算用戶之間的相似度時會出現一定的誤差。

該文考慮到用戶的評分最大值可能一定程度上構成了用戶評價體系的一部分，提出了一種改進型相似度的協同過濾算法，即引入了用戶差異因子，改進了原有的相似度計算方式，在相似度計算中，能夠起到一定的區分用戶的作用，因此能夠得到較為準確的相似度，從而提升推薦的準確度。

根據在Spyder平臺基于python3.8仿真后得到的數據表明，引入用戶差異因子后的改進型皮爾遜相似度計算方式能夠降低平均絕對誤差(MAE)，可以說該改進型協同過濾算法在準確度方面的性能有一定的提升。但是當鄰居個數(k)選取較大時，MAE值沒有較大的改善，未來值得進一步探討。

盡管經過改進后的協同過濾算法改善了傳統的協同過濾推薦算法忽略每個用戶擁有各自的評分差異，但是依然存在一些問題。首先，該算法增加了一定的計算量，提升了計算的復雜度；其次，沒有解決協同過濾算法存在的冷啟動問題；最后，將數據集劃分為測試集與訓練集并沒有解決ml-1m數據集中存在稀疏性的問題。因此，改進的協同過濾算法仍然需要進一步的完善。