擬靜力試驗中摩擦力的影響及去除方法

王志宇，唐貞云，胡云強

（1.北京工業大學城市與工程安全減災教育部重點實驗室，北京 100124；2.首創經中（天津）投資有限公司，北京 100026；3.中國建筑土木建設有限公司，北京 100079）

引言

抗震試驗是土木工程領域的重要試驗方法，隨著理論與設備的進步，目前主要的抗震試驗方法主要有［1-2］：擬靜力試驗、擬動力試驗、振動臺試驗和混合動力試驗。在試驗過程中，會存在一些試驗誤差的影響，如：加載控制誤差、測量誤差、加載系統中的摩擦力誤差、反力裝置變形多帶來的誤差以及其耦合誤差等。試驗誤差會導致在抗震試驗中，荷載加載不準確，得到的試驗數據不準確等。擬靜力試驗作為抗震試驗中常見的試驗方法，在擬靜力試驗中豎向作動器需要對試件提供恒定的豎向力，水平作動器提供水平方向的往復荷載，這時在豎向作動器與上部反力裝置之間就會產生摩擦力，摩擦力會影響試件的水平恢復力即水平方向同時存在恢復力與摩擦力，會使得傳感器測得的恢復力不準確，對試驗結果產生不利影響。

在擬動力試驗中，計算誤差和系統誤差是主要影響因素［3－4］，李暄等［5］提出在擬動力試驗中，對于大剛度結構或構件，位移控制容許值很小，位移控制誤差累計會對試驗結果產生不利影響；李玉順等［6］對擬動力試驗中的位移控制過程中產生的誤差進行分析，說明了下沖誤差減少了系統阻尼，增加系統能量，使結構地震反應增大，而過沖誤差則相反；陳再現等［7］研究了在子結構擬動力試驗中即使梁柱線剛度比很大剪切模型的時候仍然存在較大的誤差。對于擬動力試驗中的誤差，可以選用合適的數值積分方法、高精度實驗設備和合理的加載控制方法等［3－4］；杜芳［8］對于擬動力試驗中的設備誤差累計采用人工精神網絡修正的方法，并通過縮尺1：2的框架試驗實例來說明方法的效果；王貞等［9］對試件出力大，連接件和支座滑移與彈性變形，導致試件實際位移與期望位移存在偏差的問題，采用PI位移外環控制。在擬動力試驗中，摩擦力的存在導致水平恢復力不準確，使得計算出的下一步位移荷載不準確，繼續加載會使得誤差累積，對試驗結果產生較大影響。

在混合試驗中，誤差主要來源于信號傳遞過程中產生的誤差［10－11］。黃亮等［12］對于混合模擬試驗中幅值比率誤差和時滯對試驗結果的影響進行分析，說明了誤差會導致作用在試驗子結構上的外力失真，并影響了數值子結構的位移峰值和穩態振幅；陳再現等［13］將正態分布隨機數引入測量誤差，證明了縮尺比為1/2，1/4縮尺模型的測量誤差與足尺模型相應測量誤差基本相當；楊澄宇等［14］分析了相對誤差與時滯的影響，以及分析步長與執行步長產生誤差誤差的影響；吳聯俊［15］從試驗設備和結構模型對混合模擬試驗的試驗結果的誤差進行分析，并提出控制誤差的方法。在混合試驗中，對試驗子結構加載時，由于摩擦力使得輸入到計算子結構的恢復力不準確，與擬動力試驗相似也會產生誤差累積。

但是，對于擬靜力試驗中摩擦力對試驗結果的具體影響研究較少，而且新型測剪力裝置承載力有限，不能適用于所有的擬靜力試驗。因此，本文以擬靜力試驗中豎向作動器與上部反力裝置之間的摩擦力為研究對象，討論其對抗震試驗結果的誤差影響，并發展了摩擦力去除方法，減小摩擦力對試驗結果的誤差影響。

1 摩擦力對擬靜力試驗的影響

1.1 摩擦力產生原因

如圖1所示，為擬靜力試驗的加載過程力學示意圖，豎向作動器施加恒定荷載N，水平作動器施加力F，試件恢復力Fh，摩擦力為f，水平方向力的關系如式（1）所示。摩擦力如式（2）所示，由兩部分組成，分別為靜摩擦力和動摩擦力：其中：fs表示靜摩擦力，其方向始終與作動器施加力F相反，且僅在加載速度為0時，即靜止時產生；μN表示動摩擦力，方向始終與加載速度方向相反，且僅在加載速度不為0 時，及滑動時產生。

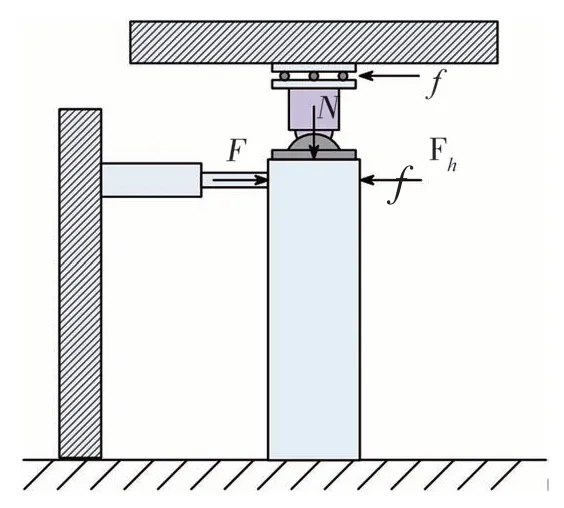
圖1 擬靜力加載示意圖Fig.1 Schematic diagram of quasi-statictesting

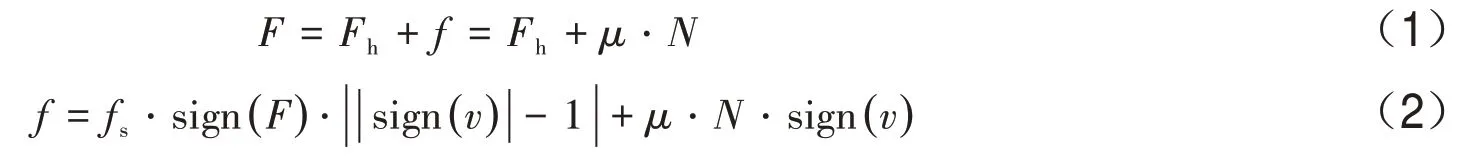
1.2 摩擦力的影響程度

將在文獻［16］中四組試驗數據中的摩擦力根據式（2）計算得出摩擦系數，見表1，摩擦系數在0.02～0.03之間，在初始加載循環由于加載荷載較小，摩擦力在水平方向占比較大，最大可達56.5%。摩擦力的存在會對恢復力產生不可忽略的誤差影響。

表1 文獻中四組案例摩擦系數及摩擦力占比Table 1 Friction coefficient and the proportion of the frictional force in the four groups of cases in the literature［16］

為了研究摩擦力對抗震試驗的影響，對大量的抗震試驗與有限元數值模擬進行文獻調查，調查一些抗震試驗與相關的有限元模擬中，有關試件軸壓比的取值范圍，如圖2所示。圖中橫坐標數據點代表所調查文獻的序號，縱坐標表示其對應的軸壓比取值，按由小到大排列。抗震試驗與有限元模擬的常見軸壓比取值范圍，普遍的軸壓比范圍在0～0.6 之間，最常見的軸壓比為0.2，0.4，0.6，其對應的軸壓力在常見的軸壓比條件下一般在500 kN到3 000 kN之間，高軸壓比條件下軸壓力會達到5 000 kN乃至13 000 kN。

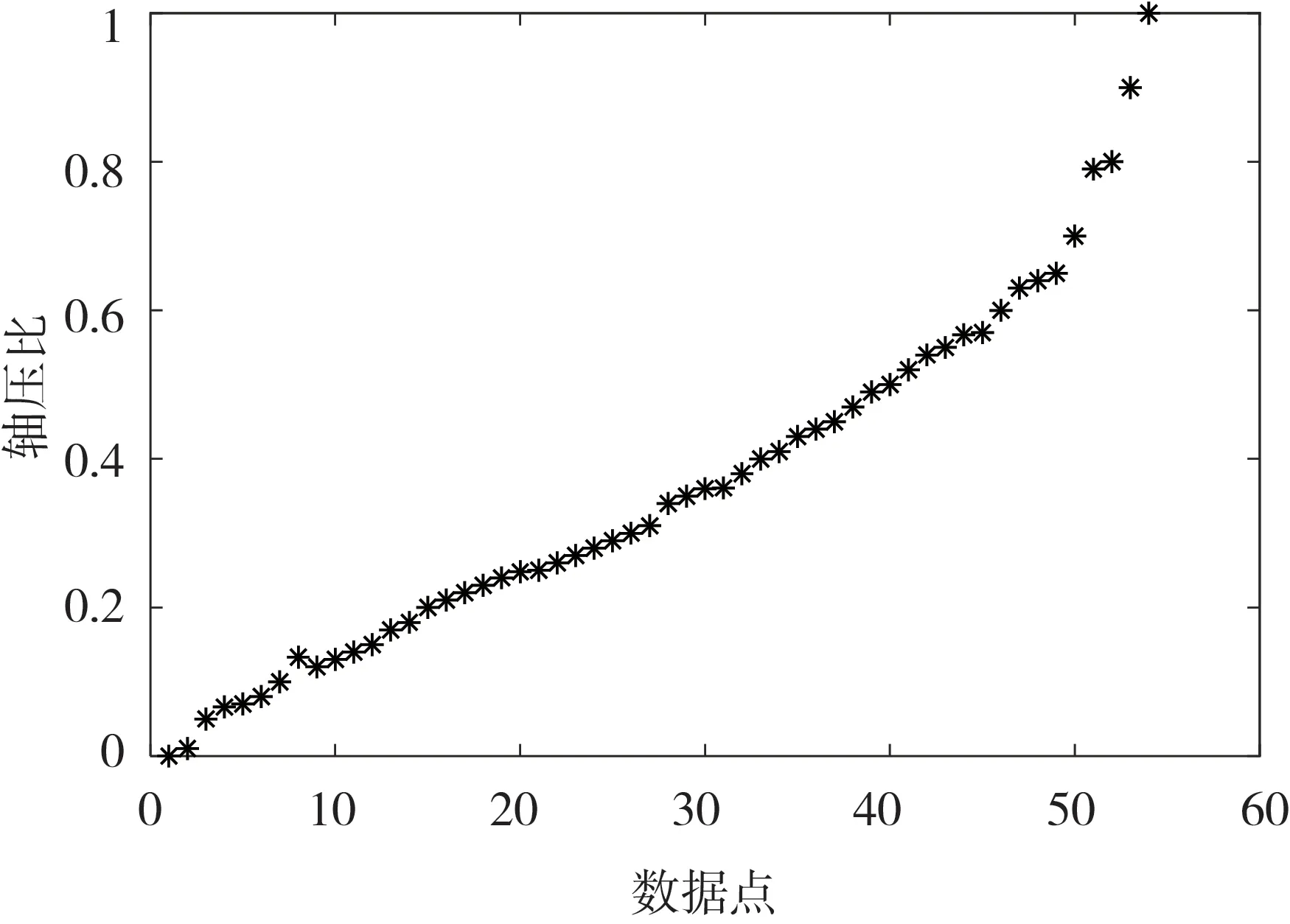
圖2 軸壓比取值范圍Fig.2 Parametric range of axial pressure ratio

圖3 中橫坐標含義與圖2 相同，現假設存在μ=0.005、0.02 與0.03 三種動摩擦系數，且作動器施加的軸力達到極值荷載，計算了動摩擦力占總水平力的比值。由圖可以看到：隨軸壓比增大，摩擦力占比增加，大部分在5%到20%之間，最大值可以達到42.11%，摩擦力較小時在10%左右。

圖3 摩擦力在水平荷載中的占比Fig.3 Proportion of friction in horizontal load

實際的加載過程中摩擦力量級基本保持不變，故對小幅值加載階段的影響更大。另一方面，試件剛度會下降，此時摩擦力在水平荷載的占比也會進一步增大，誤差更高。故在擬靜力試驗中摩擦力對試驗初始階段以及恢復力下降階段影響更大。

1.3 對抗震性能評價的影響

以一k1=30 kN/mm，α=0.13，fy=240 kN，uc=20 mm 三折線模型為結構的滯回模型，根據式（2）填加μ=0.02～0.03，N=2 000 kN 的摩擦力，如圖4（a）所示為填加μ=0.02～0.03 時的滯回曲線對比，可以看出摩擦力存在時滯回曲線會向外擴展，如圖4（b）所示為μ=0.02時的摩擦力。

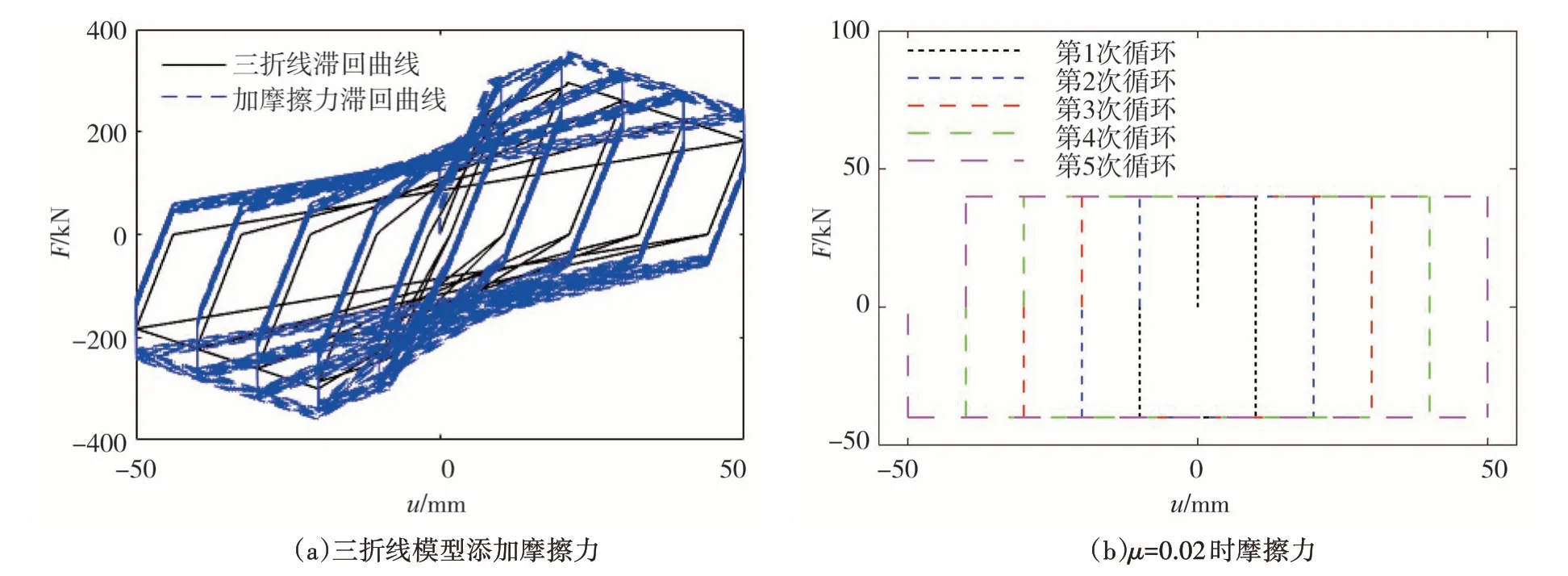
圖4 三折線模型數值模擬結果Fig.4 Numericalresultsbasedontrilinearmodel

如圖5所示為填加μ=0.02～0.03時，不同摩擦力條件下，其抗震性能參數誤差值變化曲線。隨著摩擦系數的增大，三折線模型的剛度誤差會增大，如圖5（a）所示為末尾循環的剛度誤差曲線，由于加載過程中試件剛度下降，試件恢復力降低，所以隨著加載的進行，摩擦力的影響也逐漸增大，最大誤差可達22%～33%。如圖5（b）所示為延性系數誤差值隨摩擦系數即摩擦力的變形曲線，可見摩擦力引起的延性系數誤差隨著摩擦系數的增大而增大，但是摩擦力對延性系數的影響不大，誤差主要體現在極限變形位置，最大誤差達7%左右。

如圖5（c）所示為等效粘滯阻尼系數誤差值隨摩擦系數變化曲線，與剛度和延性系數相同，等效粘滯阻尼系數誤差也隨著摩擦系數的增大而增大，第一條曲線為初始加載循環的等效粘滯阻尼系數誤差曲線，可見在初始階段，其等效粘滯阻尼系數誤差高達400%，后續的加載循環也達到了50%～150%。

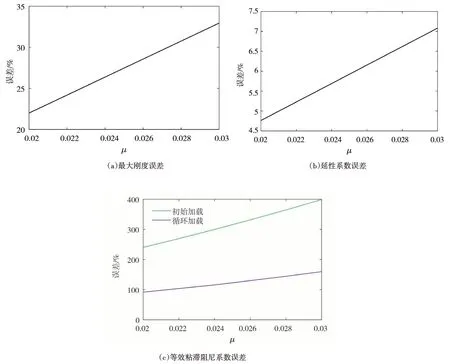
圖5 摩擦力對基于三折線模型的抗震性能參數影響Fig.5 Influence of friction on seismic performance parameters based on trilinear model

對三折線模型填加μ=0.005的較小摩擦力，剛度誤差最大為5.46%，延性系數誤差為1.41%，等效粘滯阻尼系數誤差在12.08%至52.49%，可見摩擦力較小時剛度誤差與延性系數誤差較小，但是等效粘滯阻尼系數誤差較大。

2 摩擦力去除方法

2.1 基本原理

如式（2）所示，擬靜力試驗中的摩擦力在正向與負向時，大致保持恒定大小，此時的摩擦力就可以簡化為一定值，在加載變向時會出現最大靜摩擦力的影響，根據這一特點可以將試驗結果中的摩擦力進行去除。如圖6所示，在滯回曲線的兩端由于靜摩擦力的影響，曲線兩端點會產生尖點，及靜摩擦力fs。將其去除后剩余的豎線段h，其大小即為動摩擦力的二倍，加載方向改變時，摩擦力方向改變。

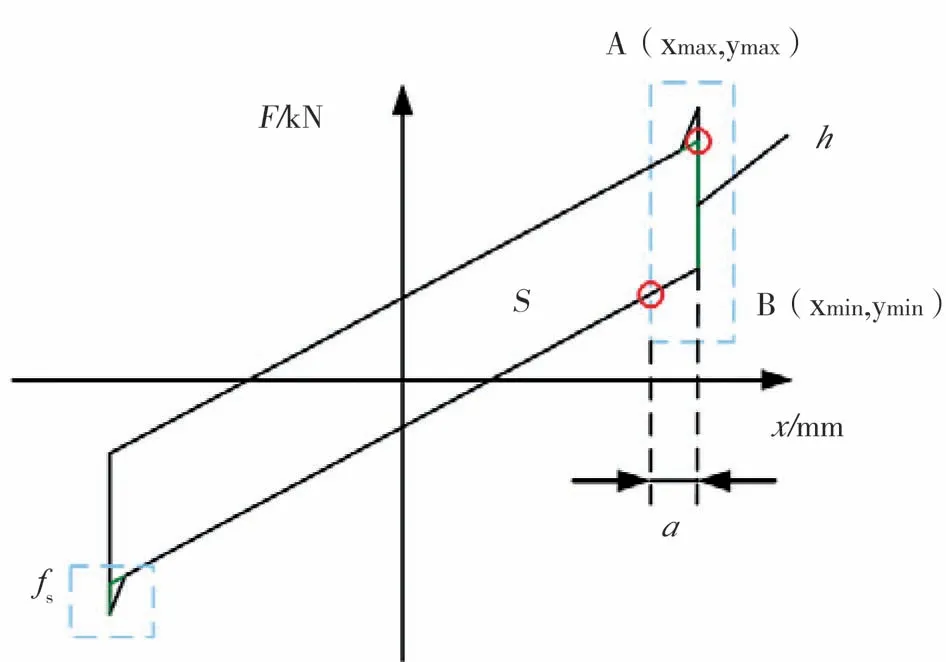
圖6 帶摩擦力滯回曲線示意圖Fig.6 Schematic diagram of hysteresis curve with friction

滯回曲線端部會存在A 點與B 點，為了識別動摩擦力的大小，需要在滯回曲線中知曉h的大小，因此首先需要去除靜摩擦力的影響。如圖7所示，由于靜摩擦力的絕對值大于動摩擦力，因此可提取滯回曲線每一個x對應的y值，依次去除y值差距最大的點，僅保留y值相差不大的點，即可得到沒有靜摩擦力影響的數據。

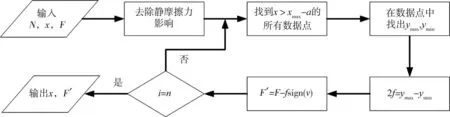
圖7 去除方法程序框圖Fig.7 Block diagram for frictionremoval method

而去除動摩擦力的方法就是在去除靜摩擦的數據兩側取一較小的區間a，在此區間中，假設y值最大的點為A點，y值最小的點為B點，將其縱坐標做差即為動摩擦力大小的二倍。由于B點相對A點偏左，因此獲取的h為近似值。如圖7所示，在程序中找出每個循環的端點值，通過計算得到h的近似值，a的取值根據試驗數據的滯回曲線而定，為避免誤差過大一般取小值，可以識別到摩擦力數值即可。

2.2 數值驗證

為了驗證固定值去摩擦力的方法，對一k1=30 kN/mm，α=0.13，fy=240 kN，uc=20 mm的三折線模型填加μ=0.02，N=2 000 kN的摩擦力，利用去摩擦的處理方法對三折線模型去摩擦力。

如圖8 所示，為對三折線模型進行去除摩擦力模擬結果，去摩擦力方法可以準確識別摩擦力的數值，三折線模擬結果相對有摩擦力誤差的三折線模型減小了摩擦力的誤差影響，下面以真實的試驗數據來驗證去摩擦力方法。

圖8 三折線模擬結果Fig.8 Trilinear model simulation results

3 摩擦力去除方法試驗驗證

在三折線模擬前提下，對文獻［16］中的試驗案例一的數據進行固定值去摩擦處理。如圖9所示，案例一為嵌入阻尼器剪力墻擬靜力試驗，豎向恒定荷載為1 622 kN，水平方向受水平荷載往復運動，最大水平位移75.6 mm，水平極限承載力為376.9 kN，利用去摩擦力方法對試驗數據進行去摩擦處理。

圖9 開縫剪力墻試驗Fig.9 Slit shear wall test

如圖10（a）所示，為對試驗數據去摩擦處理后的滯回曲線與測剪力裝置去除摩擦力后的滯回曲線準確值的對比，通過圖10（a）可以看出：利用程序去除摩擦力后，大幅度減小摩擦力的數值大小，尤其是在滯回曲線的端部即最大靜摩擦力得到良好的處理。

圖10 滯回曲線對比Fig.10 Comparisonofhysteresiscurveafterremovingfriction

如圖10（b）所示，為滯回曲線中一滯回環對比，可以更清楚地看到去摩擦處理后的滯回曲線更加接近準確值，在加載的過程中，摩擦力近似于一固定值，加載變向處存在的最大靜摩擦力也得到了較好的處理。通過對試驗數據的處理，從滯回曲線上看，整體上達到了去除摩擦力的處理效果。

為了更好地判斷摩擦力去除效果，對試驗數據的力時程曲線進行處理比較，如圖11所示，力時程曲線無論是在加載過程中還是峰值點，與準確值對比去摩擦力后的曲線基本與之吻合。去摩擦力方法是在滯回曲線的端部識別摩擦力的數值大小，識別的摩擦力數值較為準確，但是由于端部的取值范圍的增大，其誤差值也會增大。

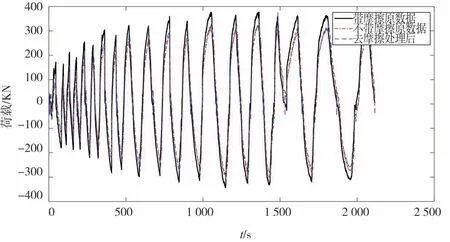
圖11 水平力時程曲線對比Fig.11 Comparisonoftime history of horizontal force

與案例一相同，對文獻［16］中的四組試驗案例都進行了去除摩擦力的處理，求得四組試驗結果通過去摩擦方法得到的恢復力絕對值之和與恢復力準確值絕對值之和的比值，以比值作為判定去摩擦力效果好壞的指標，結果見表2。

表2 摩擦力去除效果Table 2 Performance of testing resultsafter removing friction

各個案例去摩擦力誤差值相差不大，若試驗數據的摩擦力越大，波動越大，其去除摩擦力的效果越不好，案例四的摩擦力在試驗過程中數值偏大且波動較大，導致去除效果沒有相對穩定的其他三組案例的效果好，但相對與帶有摩擦力的原數據已有較好的去除效果。

對文獻［16］中的四組試驗數據進行去摩擦處理，由2.2 節可知摩擦力對壓剪試驗的剛度以及等效粘滯阻尼系數的影響較大。在試件加載的初始階段水平荷載較小，摩擦力在水平方向占比較大，故對初始剛度的影響較大，由圖5（c）可知：在加載的初始階段其等效粘滯阻尼系數誤差較大。故對初始剛度以及初始階段的等效粘滯阻尼系數誤差進行對比，見表3，程序去除摩擦力對數據結果誤差值有較好的效果，由于案例四的摩擦力數值較大且分布較為紊亂，故初始剛度誤差去除效果較差。

表3 文獻中四組案例摩擦力引起的誤差值Table 3 Error values caused by friction in four cases in the literature［16］

4 結論

本文通過分析與模擬就摩擦力對擬靜力試驗的影響與去除方法進行研究，得到如下結論：

（1）在擬靜力試驗中，豎向加載裝置與反力架之間存在的摩擦力導致得到的恢復力不準確，摩擦力通常占總水平力的10%～20%，最大可達到約42%。因此導致得到的抗震性能參數不準確，對μ=0.005的小摩擦力剛度誤差可達5.46%，等效粘滯阻尼系數誤差可達52.49%。

（2）對于摩擦力對抗震試驗產生的影響，發展了對試驗數據中摩擦力進行離線去除方法，進行去摩擦力處理后減小了試驗誤差，使得試驗數據更加準確。對于波動較小的數據，去除摩擦力后，摩檫力占總水平力的大小可從約10%減少至4.33%以下。對于波動較大的數據，也可將摩擦力占比從37.33%減少至13.56%以下。