非線性多智能體系統的固定時間包含控制

余 湛，唐朝君，謝 挺

（重慶理工大學 理學院，重慶 400054）

0 引言

近年來，多智能體系統的協調控制一直是控制領域研究的熱點。一致性問題作為協調控制研究的一個基本問題，受到了特別關注。如果系統中有多個領導者，相應的問題則被稱為包含控制問題，它研究如何通過設計分布式協議驅使跟隨者收斂到由領導者形成的凸包內。包含控制問題在軍事和民用領域都具有廣泛應用，并取得了許多有價值的成果[1-4]。

在一致性問題的研究中，收斂速度被公認為是評價一致性協議的一個重要性能指標。在大多數關于一致性問題的早期文獻中，只有在時間趨于無窮時才能達到一致。為了提高收斂速度，一些研究者設計了有限時間的一致性協議。值得注意的是，有限時間一致性的收斂時間依賴于智能體的初始條件。由于初始條件通常不能預先得到，因此不能保證在規定時間內收斂。幸運的是，近年來，研究人員為了解決初始條件的限制，在一致性問題中引入了固定時間一致性協議。文獻[5]研究了無向網絡拓撲下的多智能體系統在固定時間內實現平均一致性問題，即固定時間平均一致性問題。文獻[6]考慮了一般有向圖下非線性多智能體系統的固定時間一致性。文獻[7]研究了具有不確定性本質非線性動力學的一階多智能體系統的固定時間一致性問題。文獻[8]研究了在有向通信拓撲結構下，具有非線性動力學和不確定干擾的多智能體系統固定時間一致性問題。文獻[9]研究了具有非線性動力學和有界不確定性多智能體系統的固定時間群體一致跟蹤問題。文獻[10]研究了非線性異構多智能體系統的固定時間領導跟隨一致性問題。文獻[11]針對有向網絡拓撲結構，研究了具有切換拓撲和非線性動力學下的多智能體系統的固定時間包含控制問題。然而，以前的工作很少關注有向通信拓撲下具有未知干擾的非線性多智能體系統的固定時間包含控制問題。

基于上述原因，本文研究了有向拓撲下具有未知干擾的非線性多智能體系統的固定時間包含控制。結果表明，在存在未知干擾和有向通信拓撲的情況下，可以解決包含控制問題。此外，還得到了收斂時間的上界。

1 預備知識及問題描述

1.1 符號說明與圖論

設R為實數集，λmin(A)和λmax(A)分別為對稱實矩陣A的最小特征值和最大特征值。對于一個給定的向量x∈Rn，表示p-范數。表示集合X={x1,x2,…,xn}的凸包。若矩陣A的每個元素都是非負的，則矩陣A是非負的。若矩陣A的所有特征值都具有負實部，則矩陣A是穩定的。如果矩陣A是非負的，并且每一行都有單位和，則稱矩陣A是隨機的。

有向圖G(A)={V,E,A}，由頂點集V={1, 2, …,n}、有向邊和鄰接矩陣A組成，用于描述系統中智能體之間的通信拓撲。G(A)的一條邊用(j,i)表示，這表示智能體i可以直接接收智能體j的信息。令鄰接矩陣A=[aij]∈Rn×n；若(j,i)∈E，則aij＞0；否則aij=0，其中aij表示權重。令度矩陣。拉普拉斯矩陣L=[lij]∈Rn×n，可以用L=D-A來表示。

1.2 問題描述

設多智能體系統是由m個跟隨者和n-m個領導者組成的。跟隨者與領導者的集合分別用VF={1, 2, …,m}和VL={m+1,m+2, …,n}表示。在文獻[11]的基礎上，設計智能體i的動力學為

式中：xi(t)、ui(t)、f(xi(t),t)、di(t)∈R分別為智能體i的狀態、控制輸入、本質非線性動力學和未知干擾。

定義1通過設計合適的協議ui(t),i∈VF，如果滿足，則稱系統（1）能夠實現固定時間包含控制。其中Co(xL)表示由領導者的狀態形成的凸包，而T表示獨立于初始狀態的固定時間。

為了推導出主要結果，給出以下假設。

假設1每個領導者都不能接受信號，對于每個跟隨者，至少有一個領導者有通往它的有向路徑。

注意：當滿足假設1時，顯然，拉普拉斯矩陣L可以寫為

式中：矩陣L1∈Rm×m，矩陣L2∈Rm×(n-m)。

假設2存在一個正常數使得

式中：常數ki≥0，且。

假設3未知干擾di(t)是連續的，并且有上界dmax，即

假設4對于所有的i,j∈VF，存在常量pi＞0滿足pjaij=piaji。其中aij是與有向圖G(A)相關的鄰接矩陣的權重。

注意：如果有向圖G滿足假設4，則稱圖G滿足細致平衡條件。該條件通常用于研究有向網絡拓撲下多智能體系統的有限時間和固定時間一致性問題[12-13]。

引理1[14]對于任何向量z∈Rn，如果存在常數p＞q≥1，則

引理2[15]如果滿足假設1，則矩陣-L1是穩定的，那么矩陣是隨機矩陣。

引理3[16]如果滿足假設4，則矩陣L1P是正定的，且定義矩陣P=diag{p1,p2, …,pn}。

引理4[17]如果存在徑向無界正連續函數，使得

其 中a,b＞0，0＜μ＜1＜v，則 稱 系 統可以實現固定時間穩定性。此外，收斂時間可以通過來估計。

2 主要結果

為實現固定時間包含控制，提出以下控制協議：

式 中：α、β、γ＞0，a＜b，p＜q，且a、b、p、q均 為正奇數。

后面的內容中，為簡單起見，在不引起混淆的情況下有時省略參數t。令，

則有

定理1滿足假設1, 2, 3, 4，且當控制參數滿足以下不等式時：

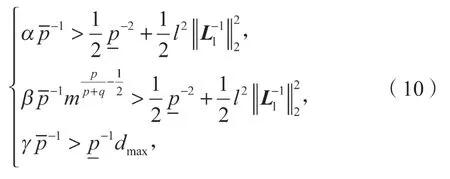
系統（1）可以實現固定時間包含控制。

證考慮如下Lyapunov函數：

根據等式（9）可以得到

根據假設2可以得到

經過簡單計算，再由引理1可以得到

則有：

式中：

定理1給出了多智能體系統包含控制的充分條件，在有未知干擾情形下，系統（1）在固定時間內實現包含控制。對此，考慮一種特殊情形，對于不帶干擾下的系統，智能體i的動力學方程如下：

定理2若滿足假設1、2、4。當控制參數滿足以下不等式時：

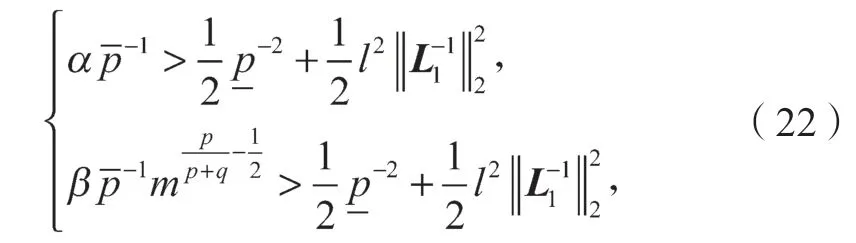
系統（21）在控制協議（7）下仍然可以實現固定時間包含控制。

3 數值模擬

例1 設某多智能體系統由2個領導者和4個跟隨者構成的。跟隨者分別記為1, 2, 3, 4；領導者分別記為5, 6，相應的通信拓撲如圖1所示。很明顯假設1和4成立。

圖1 例1對應的通信拓撲圖Fig.1 Corresponding communication topology with example 1

智能體的動力學由等式（1）描述。令，f=(xi,t)=xisint，d(t)=[sint, 0.5sint, -sint, 1.5sint]T，很明顯，假設2, 3也成立。經過計算，可以取P=diag(2/5,3/10, 1/2, 5/7)，則可以選擇控制參數分別為b=7，a=p=3，q=5，α=30，β=40，γ=20，使得參數滿足不等式（10）；隨機生成初始狀態xF(0)=(7, 4, -8, 3)T，xS(0)=(6, -9)T，則有δ(0)=(9.4, -1.8,-14.7, 14.6)T。跟蹤誤差狀態隨時間變化曲線如圖2所示。很明顯，δ逐漸收斂到0，即固定時間包含控制問題得以解決。

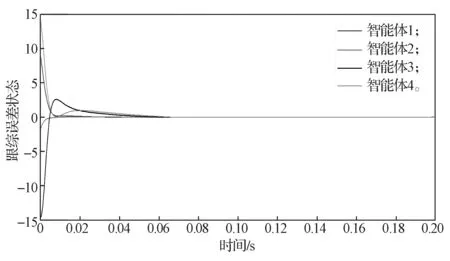
圖2 帶干擾情況下的跟蹤誤差狀態隨時間變化曲線Fig.2 Time-dependent tracking error state curves with disturbances

例2 考慮的多智能體系統由5個跟隨智能體（分別用編號1～5表示）和2個領導智能體（分別用編號6、7表示）構成的。相應的通信拓撲如圖3所示。智能體的動力學由式（21）描述。令f(xi,t)=xicost；經過簡單計算可以選擇控制參數分別為b=7，a=5，p=3，q=11，α=32，β=38，γ=22，使得滿足不等式（22）；隨機生成初始跟蹤誤差狀態為δ(0)=(2, -15,-3, 5, 12)T。跟蹤誤差狀態隨時間的變化曲線如圖4所示。很明顯，δ逐漸收斂到0，即固定時間包含控制問題得以解決。

圖3 例2對應的通信拓撲圖Fig.3 Corresponding communication topology with example 2

圖4 不帶干擾情況下的跟蹤誤差狀態隨時間變化曲線Fig.4 Tracking error state curves with time without disturbances

4 結語

針對有向拓撲情形下的多智能體系統，提出了一種固定時間控制協議，用以解決有向拓撲下非線性多智能體系統的包含控制問題。結果表明，該算法所提出的控制協議對未知干擾具有魯棒性，且收斂時間與智能體的初始條件無關。最后，給出兩個例子，證明了理論結果的有效性。

本研究只對非線性多智能體系統固定時間包含控制問題進行了初步研究。在今后的工作中，還要很多重要問題需要解決，主要有：

1）本文研究的有向網絡拓撲是在滿足細致平衡條件下的，如果對于更具有一般性的有向網絡拓撲，得到的結論也許是相似的，此時的應用范圍將會更加廣泛。

2）在控制工程中，常用的是高階的控制系統，本文研究的是一階多智能體系統，在今后的研究中，考慮利用滑模控制有助于研究解決二階控制系統。