一種面向三元空間相關Poisson過程的控制圖設計

吳蒼, 司書賓

1.西北工業大學 機電學院, 陜西 西安 710072; 2.蘭州理工大學 機電學院, 甘肅 蘭州 730050

生產過程中對異常因素的識別和診斷是維持過程穩定、安全運行的重要環節。過程監控方法目前已從生產制造領域發展到服務、醫療和交通等領域,對過程中的異常防微杜漸,能夠有效避免大的質量和安全問題。近年,隨著傳感技術和計算機技術的發展,對復雜過程安全性、可靠性和高效性能的監控提出了更高的要求。例如,在缺陷檢測方面,具有多種質量特性的工業產品中經常出現不同類型的缺陷,這些缺陷之間有可能相互作用[1];在醫療領域,某一時間段內,相鄰區域感染某種疾病的人數存在相關性[2]。

控制圖是統計過程控制領域的一種重要工具。通過對過程數據的采集、分析、計算和打點,實時監控過程的運行狀況,并對過程異常及時報警,從而達到監控的目的。根據過程數據的維度,其分為單值控制圖和多元控制圖。常見的單值控制圖有適用于監控連續變量的休哈特圖(Shewhart chart)、EWMA (exponentially weighted moving average)圖和CUSUM (cumulative sum)圖;監控一元離散變量的有c圖、u圖等。這些控制圖應用范圍很廣,但是其假設觀測值是獨立同分布的,直接將其運用到多元情形會忽略數據間的關聯性。為此，多元控制圖應運而生,主要包括用于監控離散變量的np圖、D圖[3]，用于監控連續變量的多元Shewhart圖(T2圖)、多元EWMA圖[4]和多元CUSUM圖。其中,np圖和D圖將多元離散數據轉化成一元數據,忽視了多元數據的相關性;多元Shewhart圖(T2圖)、多元EWMA圖和多元CUSUM圖不但研究了多個變量,并且同時考慮了變量之間的相關性,但這些控制圖假設變量服從正態分布。綜上所述,這些控制圖在多元離散過程監控中有局限性。

因此有必要建立一種針對多元離散型過程數據的控制圖。最初,Niaki和Abbasi[5]考慮把多元Poisson分布轉化為近似的多元正態分布進而采用T2控制圖監控。但當數據的均值較小或者存在很多零值時,這種近似會產生較大誤差。Chen等[6]假設Poisson過程的參數服從多元對數正態分布,并構建多元EWMA控制圖監控多元Poisson過程,但這一模型忽視了不同維度數據間的空間關聯性,在應用中有一定的局限性。He和龍威等[7-8]分別在等方差和異方差多元Poisson模型基礎上,構建了CUSUM控制圖。這類模型的相關性度量不夠靈活,不適應如非線性或對稱性的關聯結構。

由于copula模型在處理非線性、非正態等結構上的優勢,在金融和經濟領域得到廣泛應用。與此同時,這一方法也被引入到多元數據建模和監控領域。Dokouhaki等[9]基于copula函數構建面向二元自相關二項型數據的CUSUM控制圖。Sasiwan-napong等[10]假設觀測值服從指數分布,應用多種copula構建T2和多元EWMA控制圖。Sukparungsee等[11]采用5種copula(Normal,Clayton,Frank,Gum-bel,Joe copula)構建T2控制圖用于監控指數型特征值。Kuvattana等[12]針對二元指數型數據構建了多元EWMA和多元CUSUM控制圖,仿真結果顯示多元EWMA控制圖的監控效果最好,并且基于Normal copula構建的多元EWMA圖可以用于監控正負相關及各種強度相關性下的漂移。針對多零值離散數據,Fatahi等[13]應用零膨脹Poisson分布(zero inflated Poisson distributions)構建基于copula的聯合概率分布監控二元稀少事件(rare event)。考慮到非正態變量,Krupskii等[14]構建了對密度函數形狀變化敏感的多元過程監測方案。Chen[15]采用Normal copula描述時間序列的自相關和多元數據的互相關,并實施了多元EWMA控制圖。近期,Song等[16]提出基于copula的非參數方案,監控二元未知分布的位置和規模信息。綜上所述,多數研究聚焦于二元或連續型數據建模及監控。這主要有兩方面原因：①把二元copula函數推廣到多元情形會產生較復雜的結構,也給參數估計帶來困難；②離散邊緣分布往往會產生不唯一的copula函數。因此,有必要探索針對三元離散數據的建模和控制圖研究。

本文以三元Poisson過程數據為對象,考慮各時刻不同維度數據的空間相關性,引入三元Clayton copula描述各維度數據的相關性,根據對數似然比檢驗理論,設計出與模型匹配的控制圖。采用馬爾科夫鏈法近似求解出多種參數變化下的平均運行鏈長,最終驗證控制圖的監控性能。

1 Clayton copula簡介

1.1 copula函數簡介

copula模型廣泛應用于描述和度量變量間的非線性的相關結構[17]。以常見的二元copula函數為例,二元變量(y1,y2)的邊緣分布函數和聯合分布函數為F1,F2和F。簡便起見,記v1=F1(y1),v2=F2(y2)，且v1∈[0,1],v2∈[0,1],copula函數記做C(v1,v2),存在如(1)式所示關系

F(y1,y2)=C(F1(y1),F2(y2))=C(v1,v2)

(1)

式中，C(v1,v2)∈[0,1],且滿足以下性質:

1) 對于所有的v1,v2∈[0,1],存在

如果邊緣分布函數F1,F2均連續,那么copula函數是唯一的,反之,copula函數往往不唯一。限于此,copula函數目前在連續型過程得到充分應用,而在離散和混合過程應用較少。

根據構造原則常常把copula分為阿基米德族和橢圓族。阿基米德函數族copula結構類似,根據生成函數的不同將其分為Clayton,Frank和Gumbel函數等。而橢圓族copula是由橢圓族函數推導而來,常見的有Gaussian和Student-t等。又根據參數的數量分為單一參數copula和多參數copula。各種類型的copula在描述相關性時有所差別[18]。Gaussian copula可以靈活地描述同等程度的正相關和負相關,并在其允許范圍內包含Fréchet邊界[18]。Clayton copula不適用于解釋負相關關系,但適用于高強度的正向相關。Frank copula在實踐中得到廣泛應用,因為Fréchet邊界包含在其允許范圍內。

1.2 Clayton copula模型

Clayton copula是阿基米德函數族中常見的單一參數模型[17],廣泛應用于金融和經濟領域。二元Clayton copula定義為

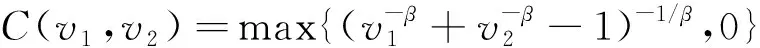
(2)

式中，β∈(-1,+∞){0}。Clayton copula是常見的單變量copula模型,生成函數為

滿足φ(C(v1,v2))=φ(v1)+φ(v2)性質。

三元Clayton copula[19]定義為

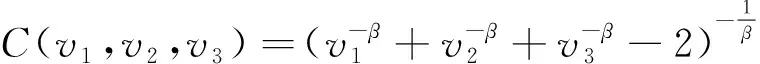
(3)

式中,β>0是唯一參數,表示任意2種變量(v1和v2;v1和v3;v2和v3)的相關性。該模型有很強的對稱性并且結構簡單,適用于三元數據建模。

2 基于copula的三元Poisson模型

實際生產過程中,多種質量特性在同一時刻的采樣值往往存在相關信息。某一時刻t采集到M個離散的觀測值,記做Yt=(Yt,1,…,Yt,M)。假設Yt服從多元Poisson過程,不同時刻采集的數據間相互獨立(如Yt,Yt-1),且每個時刻的觀測值存在空間相關性(如Yt,1,Yt,2)。考慮Yt的空間相關性,用copula來構建其聯合概率質量函數。假設對所有t=1,…,T,向量Yt=(Yt,1,…,Yt,M)的聯合分布為

F(Yt;Θ)=C(F1(Yt,1),F2(Yt,2),…,FM(Yt,M);β)

(4)

式中：β代表copula參數；Fi代表邊緣累積分布函數,i=1,…,M。

對于二元Poisson過程,在時刻t獲得的2個觀測值可以表達為向量Yt=(Yt,1,Yt,2),其聯合分布和概率質量函數分別表示為

(5)

同理,三元Poisson過程中變量Yt=(Yt,1,Yt,2,Yt,3)的聯合分布和概率質量函數分別表示為

(6)

三元Poisson過程的協方差矩陣表示為

(7)

式中，apq=aqp且apq=cov(Y*,p,Y*,q),p,q=1,2,3。根據協方差的定義結合copula理論可以計算

式中，E(Y*,p)是Y*,p邊緣分布的均值,(Y*,p,Y*,q)的二元聯合概率質量函數為

hpq(Y*,p,Y*,q;β,λp,λq)=

顯然,對于Poisson分布每個維度變量的取值范圍是非負整數集。由于各變量的協方差不恒定,本模型也屬于異方差模型。

實踐中,分布參數λ及copula參數β往往是未知的,需要根據一系列穩態觀測值估計這些參數。兩階段最大似然估計法,也稱作IFM(inference functions for margins)方法[20],是一種常用的多元copula模型的參數估計方法,表述如下:

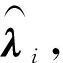
(8)

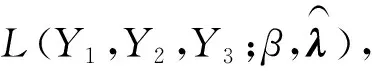
(9)

兩階段估計法在連續情形效果顯著,并得到了廣泛應用。而在離散情形下,估計參數在小維度情形很有效,對于大維度數據的效果次之[20]。

3 三元CUSUM控制圖設計

針對多變量監控問題,聯合監控多個變量比單獨監控一個變量更加容易發現過程異常[19]。考慮到空間相關性建模并獲得適用的受控模型及參數后,需要結合數據特點及控制圖原理設計出適用的控制圖。本文結合第2節的三元相關Poisson數據模型,設計多元CUSUM控制圖。假設同一時刻的三元Poisson數據存在空間相關,而不同時刻的數據間相互獨立。記t時刻的三元Poisson數據為Yt=(Yt,1,Yt,2,Yt,3),t=1,…,T,各個維度的參數記做λ=(λ1,λ2,λ3)。假設受控狀態的Poisson參數為λ0，偏移發生后變化為λc，變點模型可表示為

根據似然比檢驗的思想,對變點存在和不存在2種情形的聯合密度函數做似然比,構造統計量

(10)

式中,f(Ym,…,Yn;λ0)和f(Ym,…,Yn;λc)是(Ym,…,Yn)分別在λ=λ0和λ=λc時的聯合密度函數。記

(11)

式中，f(Yi)是概率質量函數。對于本文所討論的二元Poisson過程,f(Yi)=hB(yi,1,yi,2);同理,三元過程中,f(Yi)=hT(yi,1,yi,2,yi,3)。基于此,似然比統計量可以進一步寫做

(12)

等價的遞歸形式可表示為

Sn=max{0,Sn-1+ln(rn)}

(13)

式中，S0=0。一旦Sn超出給定的控制限h則會報警,意味著存在變點m,即Poisson參數λ發生了改變;否則,認為過程參數λ沒有顯著改變,即過程處于受控狀態。

4 仿真實驗與分析

4.1 多元相關Poisson數據的生成

基于copula模型生成多元數據是建立在條件分布基礎上的。由于copula模型的多樣性,數據生成存在一定差異。本節以三元Poisson過程為例,生成基于Clayton copula的隨機數據。記變量v1和(v1,v2)的條件概率密度函數分別為C1(v1)和C1(v1,v2),存在

另記Ck(vk;v1,…,vk-1)為條件分布,即給定(v1,…,vk-1)條件下vk的條件分布。對三元變量問題,k=1,2,3。若分子分母同時存在且分母不為零時

Ck(vk;v1,…,vk-1)=

(14)

當k=1時顯然存在C1(v1)=v1,當k=2,3時可以推算出

生成一組三元Poisson數據的過程如下所示：

1) 從均勻分布U(0,1)中隨機生成v1;

2) 從均勻分布U(0,1)生成隨機數作為C2(v2;v1)的實際值,結合v1求解方程得v2;

3) 從均勻分布U(0,1)生成隨機數作為C3(v3;v1,v2)的實際值,結合v1和v2求解方程得v3;

4) 應用Poisson分布的反函數得到一組數據(y1,y2,y3),其中,y1=F-1(vi),i=1,2,3。

4.2 參數估計

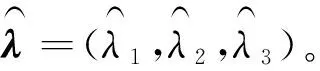
4.3 馬爾科夫鏈近似求解平均運行鏈長

目前,主流的用于評價控制圖監控效果的指標是平均運行鏈長(average run length,ARL),即運行鏈長(RL)的期望值。而運行鏈長RL是指從開始到第一次失控報警的樣本點數目。本文采用馬爾科夫鏈(Markov chain)近似計算多元CUSUM控制圖平均運行鏈長。控制限記做h,受控的多元Poisson參數為λ0=(λ1,λ2,λ3),目標參數記做λc=θλ0,失控參數λd=(δ1λ1,δ2λ2,δ3λ3)。首先將受控區間分為ne等分,每一段的長度Δ=h/ne,每部分區間可表示為[(k-1)Δ,kΔ),k=1,2,…,ne。一旦統計量落入區間k,認為統計量近似取區間中點值,即(k-0.5)Δ。假定轉移矩陣P中的每一個元素pjk代表統計量從區間j轉移到區間k的概率,記做

pjk=P{Sn∈[(k-1)Δ,kΔ)|Sn-1=(j-0.5)Δ}

(17)

式中，j,k=1,2,…,ne。轉移概率的計算首先需要列舉出所有可能的三元Poisson數據組合,并分別計算其聯合概率。需要注意的是,計算受控ARL(L0)時,采用hT(Yt;λ0,β);反之,計算失控ARL(L1)時,采用hT(Yt;λd,β)計算。對轉移矩陣做一些變換即可得到表示ARL的向量L

L=(I-P)-11

(18)

式中,I是單位矩陣,1是全為1的列向量。由于初始值S0=0,因此向量L的第一個元素即為ARL的近似值。值得注意的是,該方法近似計算ARL的精確程度受到間隔的等分數ne影響。ne越大,計算的ARL越接近真實值,但是計算時間會相應增加。

4.4 三元CUSUM控制圖的監控效果

在缺陷監測和疾病預防的背景下,本文關注多元Poisson數據的異常增長,采用單側向上的控制圖考察監控效果。同理,單側向下或雙側控制圖可以根據實際情況選擇。鑒于多元Poisson數據的特點,控制圖的控制下限不做要求,控制上限記做h。在階段一,給定適當的受控ARL, 采用馬爾科夫鏈的方法搜索控制限h。

對三元Poisson過程的每個維度分別考慮3種異常參數,則會有33=27種組合。顯然,實現每一種組合的異常參數集合是不現實的。因此,考慮了9種組合方式。每一種組合方式中,參數變化幅度可記為δ=(δ1,δ2,δ3),又因為受控參數λ0=(λ1,λ2,λ3),則異常參數λd=(δ1λ1,δ2λ2,δ3λ3)。此外,控制圖設計中的目標參數λc=(θλ1,θλ2,θλ3)。考慮到設計過程的便利性,設定為1.1,1.5和2.0。

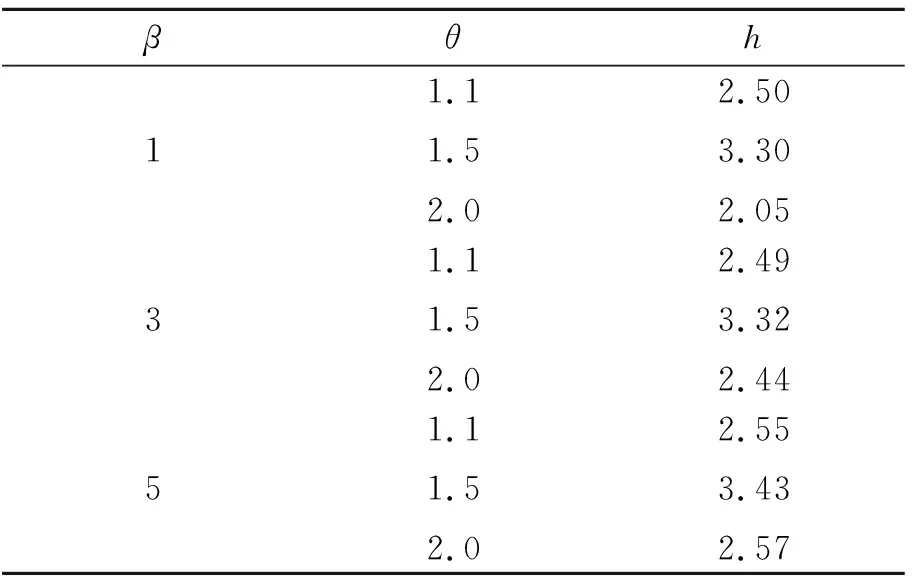
表1 L0=200時多元CUSUM控制圖在3種copula參數和3種目標參數下的控制限

設定λ0=(10,10,10)且L0=200,表1和表2分別展示了3種copula參數和3種目標參數條件下的控制限和失控平均運行鏈長。其中,序號1～3僅有1個維度的參數發生向上階躍,4～6有2個維度發生變化,7～9表示3個維度均發生變化的情形。文獻[4,7]采用一種表征馬氏距離的變化尺度(shift size)量,或稱為非中心性參數(non-centrality para-meter)

Ss=[(λc-λ0)Σ-1(λc-λ0)′]1/2

式中,λ0和λc分別是受控和失控的參數向量。如公式(7)所示,Σ是協方差矩陣。非中心性參數能夠度量過程參數的整體變化。對于2組異常參數,如果其非中心性參數相等,則L1也相當。例如,表2中序號1代表的異常參數的變化幅度為δ=(1.1,1,1),其性能與δ=(1,1.1,1)及δ=(1,1,1.1)情形相當。 同理,序號6代表的異常參數的變化幅度為δ=(2,1,2),其性能與δ=(2,2,1)及δ=(1,2,2)情形相當。因此,表2所列出的9種組合方式足夠代表全部27種異常情形的ARL性能。從表2中可以看出,當參數有變化時,L1值均小于L0值,即L0=200,說明本文方法可以檢測多元Poisson過程均值向上偏移。并且,隨著參數變化的幅度值不斷增大,L1越來越小。對于一種特定的失控狀態,隨著copula參數的增加,平均運行鏈長普遍增大。也就是說,多元過程的空間相關性越來越強時,監控異常變化的難度也越來越大。對比3種目標幅度值來看,θ=1.1的控制圖對δ1=δ2=δ3=1.1(序號7)的異常情況效果好;θ=1.5的控制圖對δ1=δ2=δ3=1.5(序號8)效果好;θ=2的控制圖對δ1=δ2=δ3=2(序號9)效果好。因此,設計多元Poisson控制圖時,對較小的變化幅度需要選擇較小的θ, 反之,對于可能存在的較大變化,選擇較大的θ可獲得更理想的效果。

表2 多元CUSUM控制圖在3種copula參數和3種目標參數下的失控平均運行鏈長

圖1展示了Poisson數據及其在多元CUSUM控制圖的應用。設定異常參數的變化幅度δ=(1.1,1.1,1.1),則目標參數的變化幅度選為θ=δ。三元Poisson數據由4.1節方法生成。圖1a)～1c)分別代表β=1,3,5時對應的多元Poisson數據,而對應的CUSUM統計量繪制在圖1d)～1f)中。每組Poisson數據包括3個維度,每個維度有20個受控數據和20個失控數據,圖中用藍色虛線分隔。紅色水平線代表在L0=200水平下的控制限。從表1中可得出在β分別取1,3,5時對應的控制限為2.5, 2.49和2.55。從圖1中可以看出,對于所列出的3種β取值,提出的方法對失控數據都有較好的檢出力。

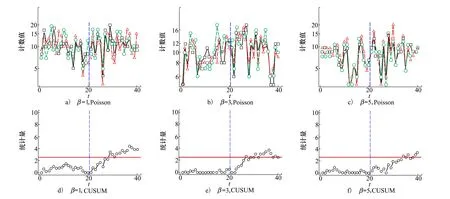
圖1 Poisson過程數據及其在CUSUM控制圖的應用(L0=200)

圖2對比了本文所提方法與文獻[3]中D圖的性能。為了便于對比,實驗假定δ=δ1=δ2=δ3,其中δ=1代表受控狀態,δ=1.1,1.2,…,2代表失控狀態。圖2a)～2c)分別展示在β=1,3,5條件下D圖和本文所提多元CUSUM控制圖在θ=1.1,1.5的ARL對比。從圖中可以看出,D圖在β=1條件下監控較大偏移量(θ≥1.2)性能優于本文所提CUSUM控制圖。當β=3,5時,本文提出的CUSUM控制圖對所有偏移量均取得更小的L1。其中θ=1.1的CUSUM控制圖對較小的偏移量監測效果最好,θ=1.5的CUSUM控制圖對較大的偏移量監測效果最好。這一點與表2的結論一致。

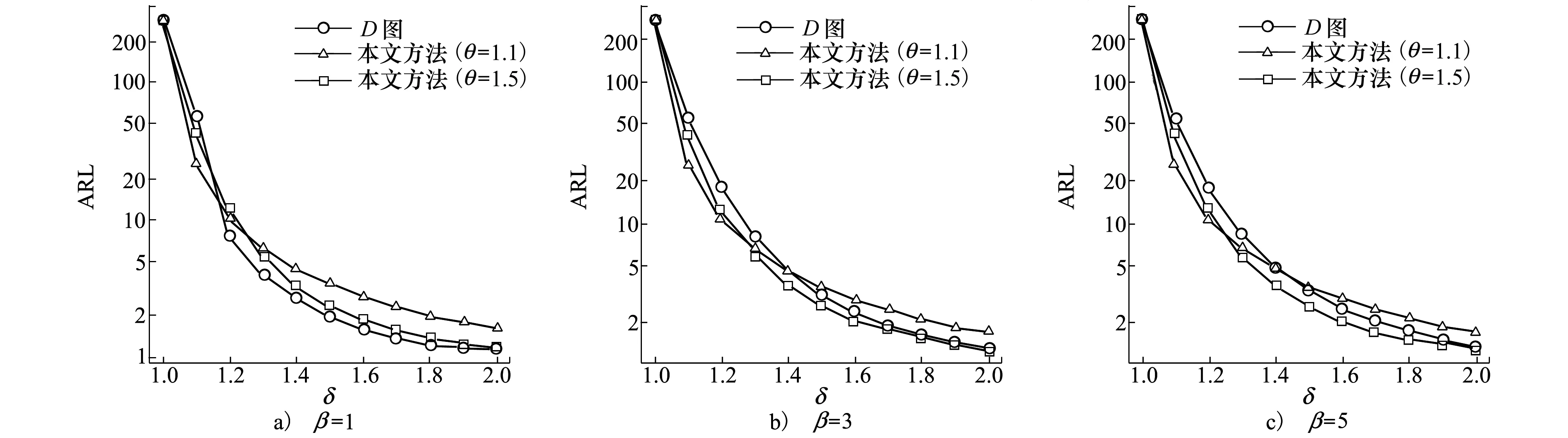
圖2 D圖與本文提出CUSUM控制圖的性能對比

5 結 論

針對具有空間對稱相關結構的三元Poisson過程監控問題,首先采用三元Clayton copula函數描述其相關性,并構建聯合分布;在假設copula參數不變的前提下,基于對數似然比檢驗方法結合聯合分布信息,推導出多元CUSUM控制圖的監控統計量;在給定初始值的前提下,利用馬爾科夫鏈方法近似求解ARL,驗證其有效性,并與D圖做對比。仿真結果表明,提出的方法能夠有效監測過程均值的向上漂移,并且目標偏移量與實際偏移量相等時可以獲得更好的監控性能。與D圖相比,當數據間的相關性較強時,提出的方法對于所有的偏移量能取得更好監控效果。在未來工作中,將進一步研究時間和空間關聯同時存在的多元數據建模及監控問題。