對數線性插值土工顆粒分析方法
沈捍明
(中鐵十二局集團第七工程有限公司 湖南長沙 410004)
1 前言
土工試驗評定級配特性時,需要知道質量百分比P小于某一特定值m的特征粒徑d(P<m)來計算曲率系數、不均勻系數等參數。但是在試驗過程中,篩網孔徑固定且不連續,不可能直接測定d(P<m)。工程中一般采用間接測定di(P<mi)及di+1(P<mi+1),其中di和di+1分別對應標準篩徑,并合理選擇mi及mi+1,使m∈(mi,mi+1),將m線性內插入[(mi,di(P<mi)]與[mi+1,di+1(P<mi+1)]點間,從而求得d(P<m)。該方法是基于m與d(P<m)的線性坐標系,但篩徑尺寸從102mm變化至10-3mm,數量級跨度較大,在此坐標系下,相鄰已知坐標點間距分布極不均勻,數據呈現非線性關系。工程中的篩分曲線展繪已考慮該問題,并采用了半對數坐標來顯著體現曲線變化趨勢,因此在特征粒徑推定時若仍采用線性插值,其估計值將產生較大偏差[1-3]。
2 插值原理
如圖1所示,設數據x經過對數運算后,位于對數坐標軸lgx上。A、B、C三點為實際測得的三個數據點,其坐標分別為(lgxA,yA)、(lgxB,yB)、(lgxC,yC)。在該坐標系下連接A、C點,過B點做水平線,與直線AC交于點B′,則B′點為y=yB對應的對數線性內插點。根據線性內插關系:
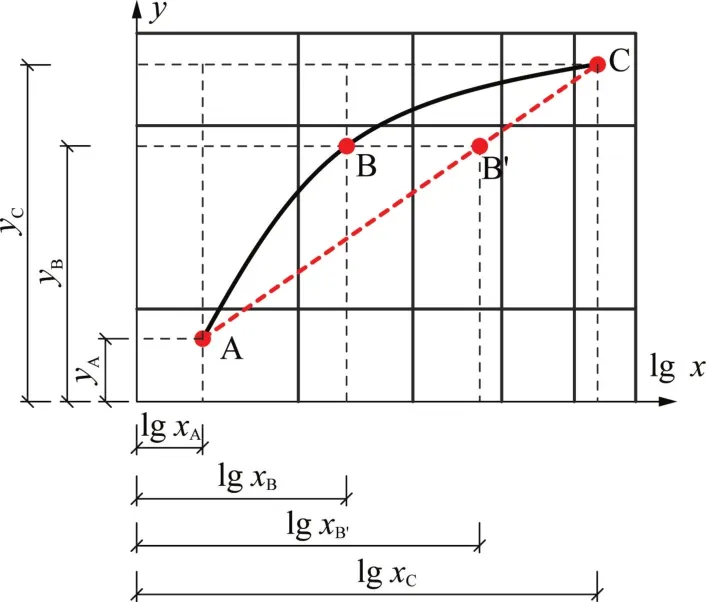
圖1 對數坐標線性插值示意

式(2)即為按對數坐標線性插值的計算公式,按指數規律變化,其與式(1)的線性內插方法不同。在已知A(xA,yA)、C(xC,yC)及B點縱坐標yC后,即可通過該式推算B點橫坐標xB′。
3 偏差分析
3.1 “跳點法”計算插值偏差
采用插值方式對數據進行預測需給定對其偏差測定的方法,以評估插值精度,這是目前大多數數據插值處理所缺失的。土工篩分試驗中,單次試驗測定數據較少,考慮采用原始數據構造“跳點法”校核插值精度:如圖2所示,設A、B、C、D為實測數據點,首先假設B點未知,AC點采用式(2)插值推算出B′點,再比對B與B′點位偏差值ΔB;假設C點未知,采用式(2)推算出C′點,比對C與C′點位偏差ΔC。依此類推,直至遍歷所有點位。該方法可以校核除首末點外的所有點位偏差[4-6]。
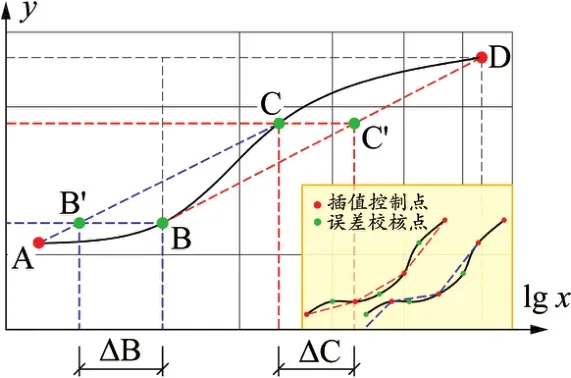
圖2 跳點校核示意
3.2 偏差分析參數選定
由前述可知,采用“跳點法”,可先按式(3)逐個計算各點位的相對偏差δ。

在插值精度理想的情況下,δ應趨于0。樣本整體的平均相對偏差越小,樣本標準差σ越小,其表征插值方法對于源數據的適應性越好,性能越穩定。和σ分別按式(4)、式(5)計算。
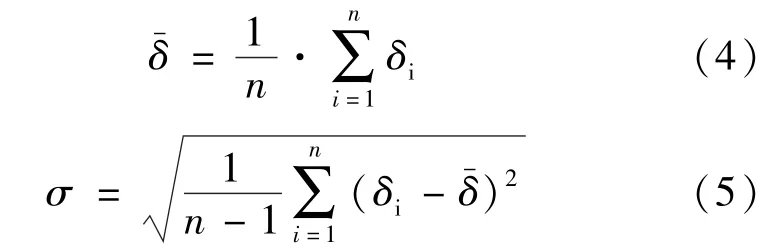
由于標準篩徑從150 mm變化至0.007 5 mm,數據變化跨度較大,雖相對偏差δ為無量綱量,考慮插值精度有限,可能存在相對偏差尺度變動較大情況,故還需采用式(6)計算變異系數輔以評估。

3.3 均值接近零時的變異系數優化
基于此,在當趨于0時,在保證式(6)中cv單調性不變的前提下,降緩其值增長速率,則考慮對其取對數處理。鑒于最小篩徑為10-4數量級,最大篩徑為102數量級,故對數底數采用104變換后cv在10-1至100數量級間浮動,較易辨別其變化特征,則定義:
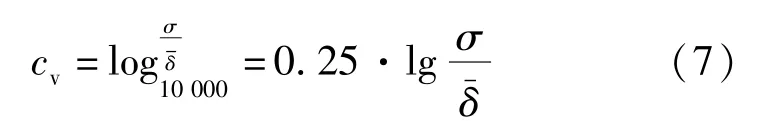
3.4 偏差系數
由前述可知,評估插值方法的偏差時,、σ、cv均越小越好。但由式(7)計算變異系數時,可能出現負數,單純取三者代數和可能存在正負抵消的情況。借鑒樣本標準差定義方法,此處定義偏差系數Ψ有:
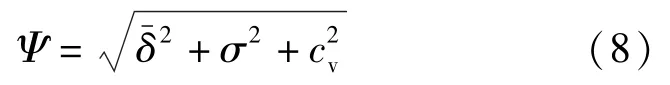
其中,、σ、cv分別由式(4)、式(5)、式(7)求得。在實際工程中,對于同一數據點,利用“跳點法”,分別采用線性插值和對數線性插值計算樣本的偏差系數,取偏差系數較小的插值方法確定的插值參數作為估計值。
4 應用實例
4.1 數據偏差分析
以大張高鐵改DIK184+000~改DIK187+150段路基填料的44組土工篩分試驗數據作為樣本,以實測的小于 40、20、10、5、2、1、0.5、0.25、0.75 mm粒徑質量百分比作為真值,分別采用線性插值法和對數線性插值法反算相應粒徑,并與真值粒徑進行對比,計算過程和比對結果分別見表1~表4[7]。
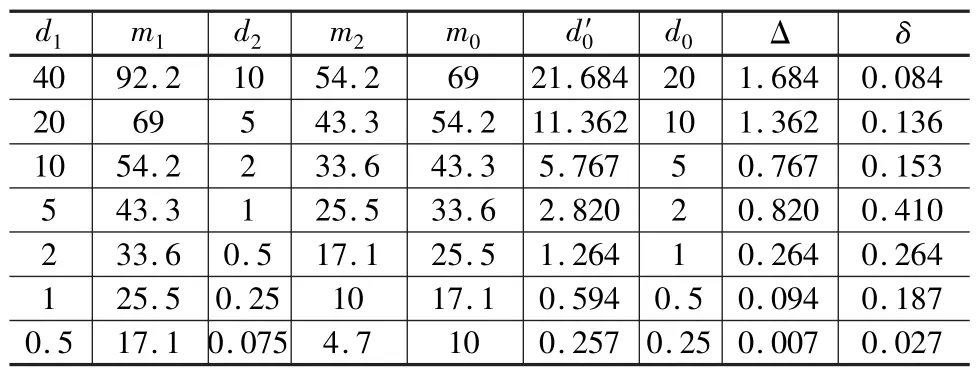
表1 線性插值計算
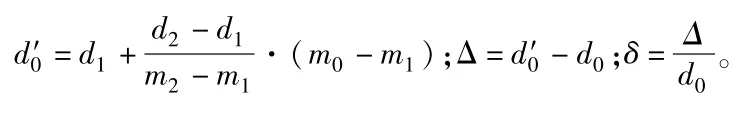

表2 對數線性插值計算
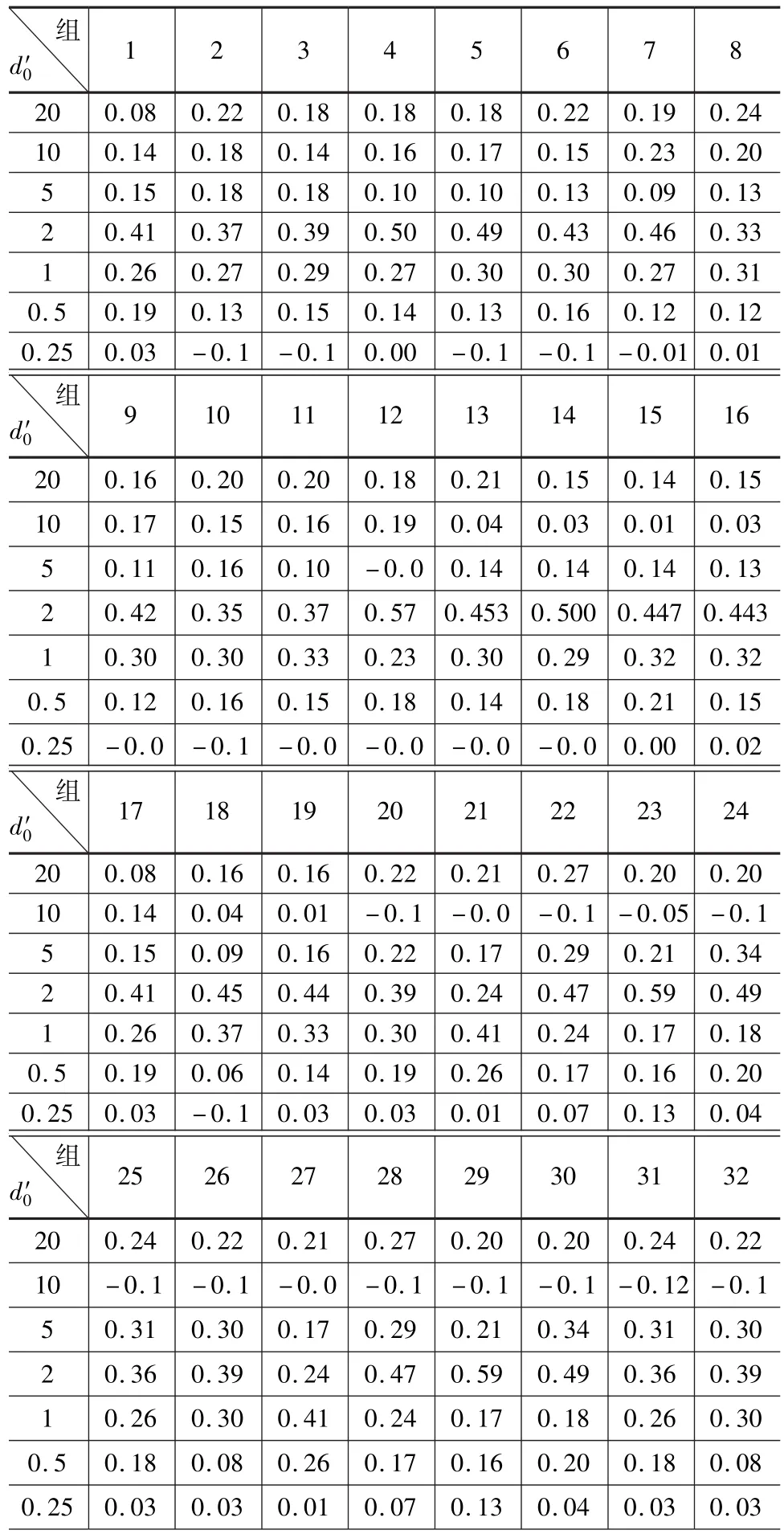
表3 各粒組線性插值數據偏差分析
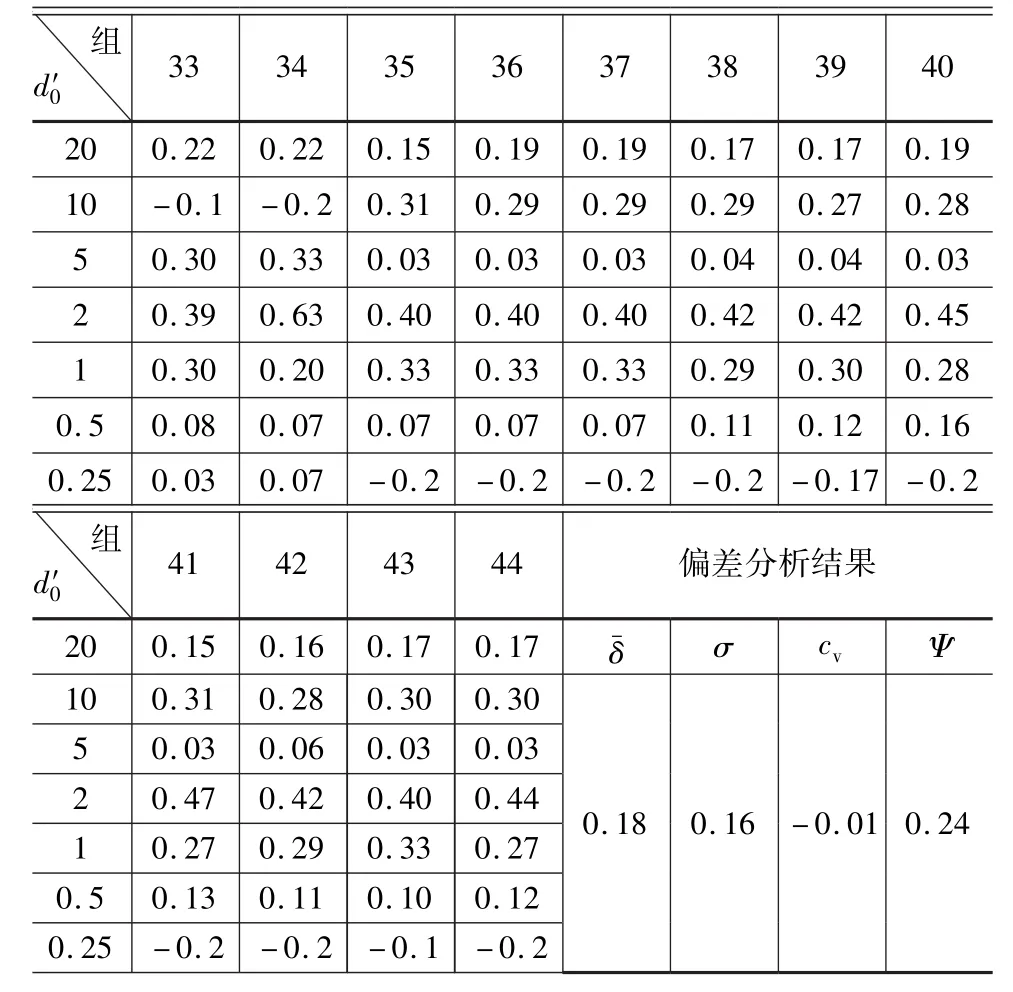
續表3
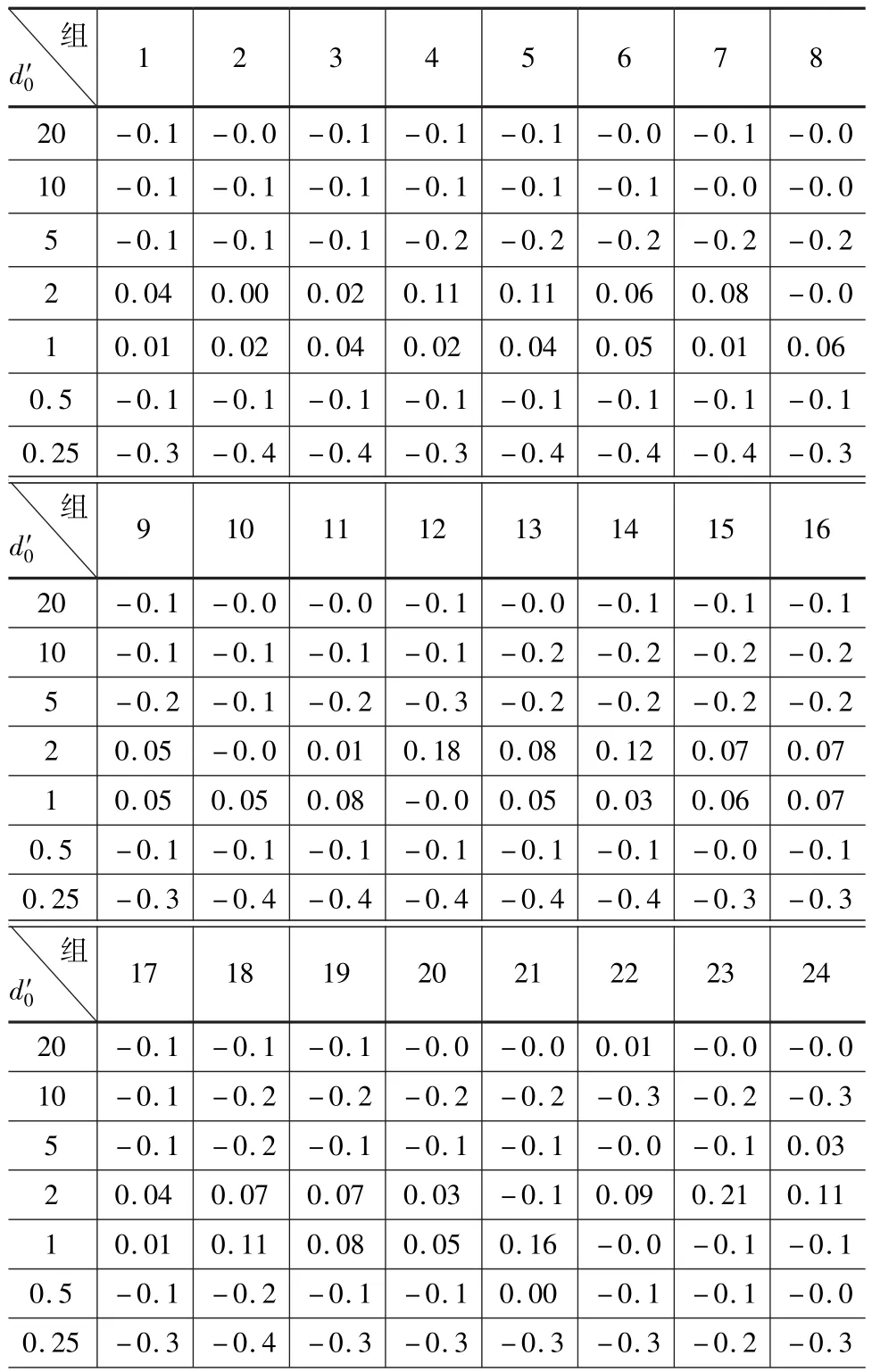
表4 各粒組對數線性插值數據偏差分析
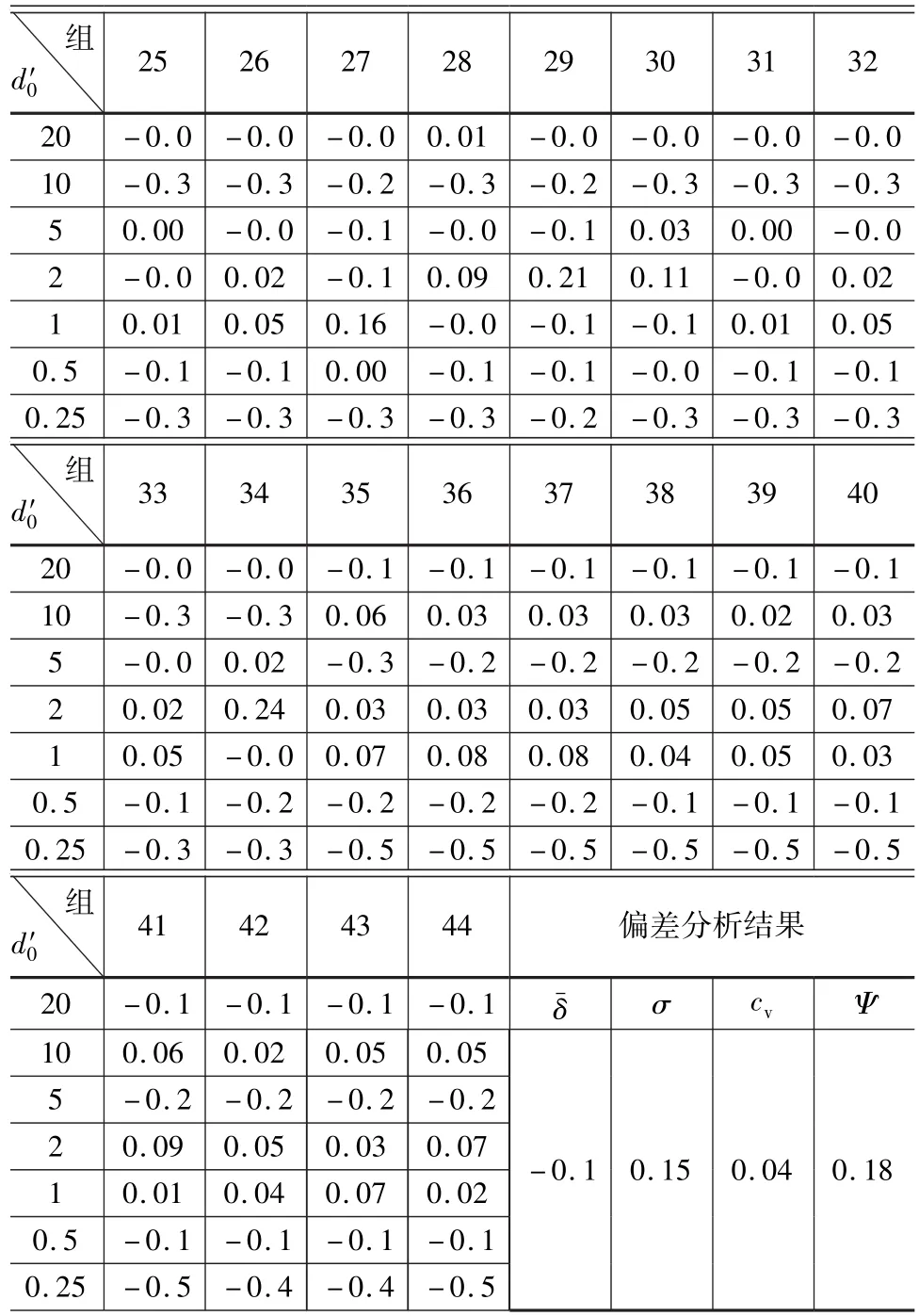
續表4
由表3和表4對照可知,對于同樣的44組試驗數據,除線性插值法的變異系數略大于對數線性插值法外,相對偏差均值、相對偏差標準差、偏差系數均大于線性對數插值法。由于偏差系數反映了插值偏差整體情況,因此對數線性插值精度優于對數插值[8-10]。
4.2 特征粒徑推算
以表2中數據為例,計算d60、d30及曲率系數和不均勻系數。
由表中數據知,60∈(54.2,69),d54.2=10,d69=20;30∈(25.5,33.6),d25.5=1,d33.6=2。 試驗中恰好測得d10=0.25,則由式(2)可知:
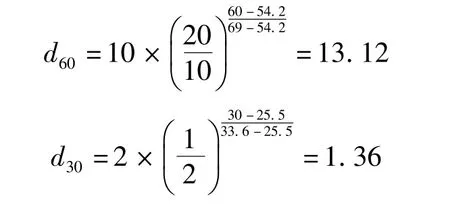
故不均勻系數:Cu=13.12/0.25=52.5;Cc=1.362/(13.12×0.25)=0.56。
5 實用化程序
本方法雖較大程度提高了插值計算的可靠性,但計算過程偏繁瑣。為適應工程中快速準確計算,為此利用CASIOfx-5800P可編程函數計算器編制通用計算程序,以滿足現場數據記錄和計算要求,程序源代碼如下:

上述代碼執行過程可實現如下功能:
(1)程序提供了“線性插值”和“對數線性插值”兩種計算模式。
(2)一次性最多支持輸入13組粒組數據。
(3)在任意指定質量百分比時,程序可根據輸入的粒組數據自動搜索相鄰的質量百分比及對應的特征粒徑。
(4)只需一次性輸入單次試驗粒組數據后,可重復計算任意質量百分比的特征粒徑,無需重復錄入粒組數據。
(5)考慮土工篩分試驗和數據記錄的習慣,程序中粒組數據的錄入按從大粒徑向小粒徑的順序輸入,且與計算結果唯一對應。若粒徑錄入順序與之相反,則計算會出錯[11-12]。
計算器程序編輯、運行界面如圖3所示。

圖3 計算器程序編輯及輸出界面
6 結論
本文通過分析線性插值法和對數線性插值法兩種方法的插值偏差,并通過大量樣本數據進行驗證,得到如下結論:
(1)重新定義的變異系數可有效解決數據數量級跨度較大、量綱不統一、均值趨于零一類樣本離散特性難以評估的問題。
(2)構造了基于對數坐標線性插值的方法,提出的“跳點法”可有效評估各類插值方法偏差。
(3)構造的“偏差系數”綜合考慮了均值、標準差、變異系數特性,可定量評估不同插值方法間的偏差大小,為在不同的樣本條件下科學選取插值方法提供了依據。
(4)對數線性插值的偏差要小于線性插值偏差,且因實用化程序的提出,實際工程中建議盡量采用對數線性插值方法。

