考慮損耗的表貼式永磁同步電機極弧系數優化

劉保泉，張洪信,2，魏士文

(1 青島大學 機電工程學院，青島 266071；2 青島大學 電動汽車智能化動力集成技術國家地方聯合工程研究中心，青島 266071)

0 引 言

表貼式永磁同步電機具有結構簡單、功率密度大、噪聲低、運行效率高等優勢，成為新能源汽車驅動電機的熱門選擇。對車用永磁同步電機而言，研究電機的損耗不僅可以保證電機安全穩定運行，而且有助于從整體上考慮永磁同步電機的設計。

為了提高永磁同步電機的整體性能，國內外學者對電機各方面性能進行了大量的優化研究。文獻[1]提出了一種內置式永磁同步電機驅動系統效率工程化優化方法，優化后電機系統效率有所提升；文獻[2]提出了一種考慮電機損耗和溫度場分析的矩形導線繞組設計與優化的方法，優化后電機能量密度有顯著提高；文獻[3]通過正交實驗法對表貼式永磁同步電機的永磁體形狀進行優化，從而降低了電機齒槽轉矩；文獻[4]在考慮鐵心飽和的情況下，采用改進的非支配排序遺傳算法的多目標優化方法，對表貼式永磁同步電機進行優化設計；文獻[5]提出了一種新的非均勻形狀永磁材料磁場分布分析模型，并在此基礎上提出了一種諧波注入永磁體形狀優化的方法，該方法可以有效降低表貼式永磁同步電機的磁場諧波和鐵損；文獻[6]針對內置式永磁同步電機，提出了一種改進的多物理和多目標優化方法，優化目標包括功率密度、溫升、價格、轉矩脈動和齒槽轉矩，并通過仿真和實驗驗證了該方法的可行性；文獻[7]提出一種適用于負載頻繁變化工況下的表貼式永磁同步電機最小損耗控制策略，通過仿真驗證了該方法優于傳統控制方法；文獻[8]提出一種采用形狀約束的連續設計靈敏度分析的內置式永磁同步電機優化方法，將該方法應用于永磁同步電機的轉子設計，驗證了其可行性；文獻[9]提出了一種利用田口法削弱永磁同步電機齒槽轉矩的優化方案，該方法優化后齒槽轉矩被大幅削弱；文獻[10]提出一種采用內嵌磁極偏移與非均勻氣隙偏心轉子相結合的優化方法，該方法有效削弱雙層內嵌式永磁同步電機的齒槽轉矩，改善電機的輸出性能；文獻[11]采用田口優化算法對永磁同步電機轉子進行優化設計，優化后齒槽轉矩降低，電機性能顯著提高。

永磁體極弧系數的優化研究方面：文獻[12]設計了具有不同極弧系數組合的分段傾斜磁極來削弱齒槽轉矩，并通過AM和粒子群優化算法總結了極弧系數和相鄰磁極傾角的最佳組合；文獻[13]提出了一種通過選擇合適的極弧系數來降低分數槽永磁同步電機固有軸電壓的方法，通過解析法和有限元法確定最佳極弧系數；文獻[14]將改進的區域消除法(DEA)、有限元法(FEM)和解析法相結合，對表貼式永磁同步電機的極弧系數進行優化，該方法優化后齒槽轉矩大大減小，計算時間顯著縮短。

綜上所述，永磁同步電機優化方面的研究成果較為豐碩，但以鐵心損耗為主，兼顧輸出轉矩峰峰值和永磁體體積的永磁體極弧系數進行優化的研究還不多見。

1 電樞繞組銅損耗模型

車用永磁同步電機繞組中通入的三相交流電由逆變器調制形成，繞組大多采用截面積較小的圓形銅導線，且電流交變頻率較低，電流在導線中分布較為均勻，幾乎不存在趨膚效應。若忽略繞組諧波電流及趨膚效應的影響，電樞繞組損耗計算公式：

pcu=mI2R

(1)

式中：pcu為電樞繞組損耗；m為電機相數；I為電樞繞組相電流有效值；R為電樞繞組相電阻。

永磁同步電機電樞繞組相電阻：

(2)

式中：K′F為考慮趨膚效應時的電阻增加系數，若忽略趨膚效應，此系數等于1；ρw為基準工作溫度時導體的電導率；N為電樞繞組每相串聯匝數；lo為繞組線圈平均半匝長度;Ao1為繞組導線橫截面積；a1為每相繞組的并聯支路數。

在溫度15 ℃時銅的電阻率ρ15=1.75×10-8Ω·m。導體電阻率與溫度有關，在電機的正常運行范圍內，溫度為t時的電阻率ρt可按下式換算：

ρt=ρ15[1+α(t-t15)]

(3)

式中：α為導體電阻的溫度系數，對于銅，α≈0.004 ℃-1；t15=15 ℃。

2 定子鐵心損耗計算模型與分析

2.1 定子鐵心損耗計算模型

作為永磁體極弧系數優化的目標函數之一，分析定子鐵心損耗是非常有必要的。

目前采用公式對鐵心損耗計算得到的結果與損耗實際值之間依然存在誤差。意大利學者Bertotti提出的鐵耗分離計算模型依然是當下應用最為廣泛的鐵耗模型。鐵心受正弦交變磁場磁化時，采用此模型能夠較為準確地計算鐵心損耗。單位體積的鐵心損耗：

pFe=ph+pcl+pex

(4)

式中：pFe為鐵心總損耗；ph為磁滯損耗；pc為經典渦流損耗；pex為異常渦流損耗。式(4)可以寫成:

(5)

式中：Bm為磁通密度幅值；f為頻率；Kh為磁滯損耗系數；Kc為經典渦流損耗系數；Kex為異常損耗系數；α為磁滯損耗系數。其中，異常損耗是由于磁疇壁不連續運動產生的巴克豪森躍變產生的損耗。

采用式(5)計算定子鐵心損耗，并未考慮磁密諧波對鐵耗計算的影響，顯然計算誤差較大。為了更準確地計算鐵心損耗，對定子各點處的磁密波形進行正交分解，將旋轉磁化視為徑向和切向兩個交變磁場；由傅里葉分解理論可知，任意周期函數都可以分解為有限個不同幅值、頻率的簡諧函數的疊加。將徑向磁密基波、切向磁密基波和諧波分解后產生的鐵心損耗疊加得到定子鐵心損耗，正交分解和諧波分解法同時應用時得到的鐵心損耗計算誤差較小。基于Bertotti模型本文采用如下公式：

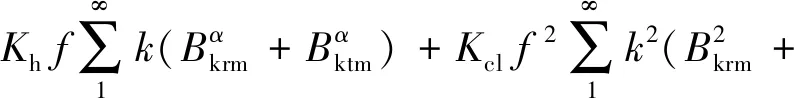
(6)

2.2 定子鐵心損耗分析

電機模型如圖1所示，各種參數如表1所示。電機控制方式為最大轉矩電流比控制，通過二維有限元仿真計算得到額定工況下電機的定子鐵心損耗如圖2所示，定子區域損耗云圖如圖3所示,額定電流轉矩仿真結果如圖4所示，電流變化如圖5所示。

圖1 永磁同步電機二維模型

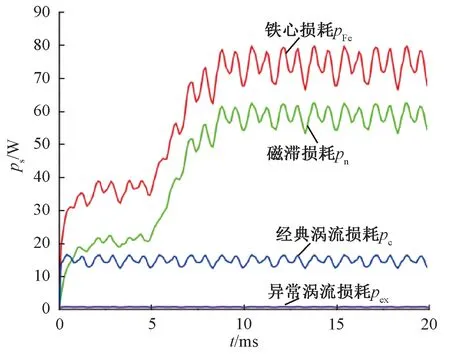
圖2 額定工況下定子鐵心損耗曲線

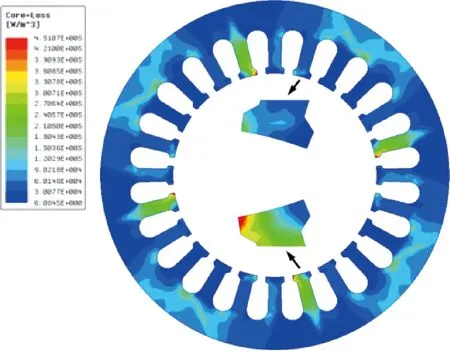
圖3 定子區域損耗云圖

圖4 額定電流下轉矩仿真結果

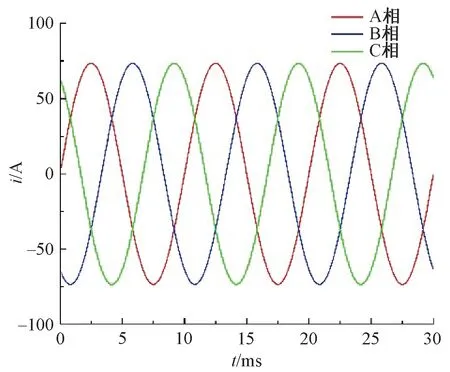
圖5 電流變化曲線

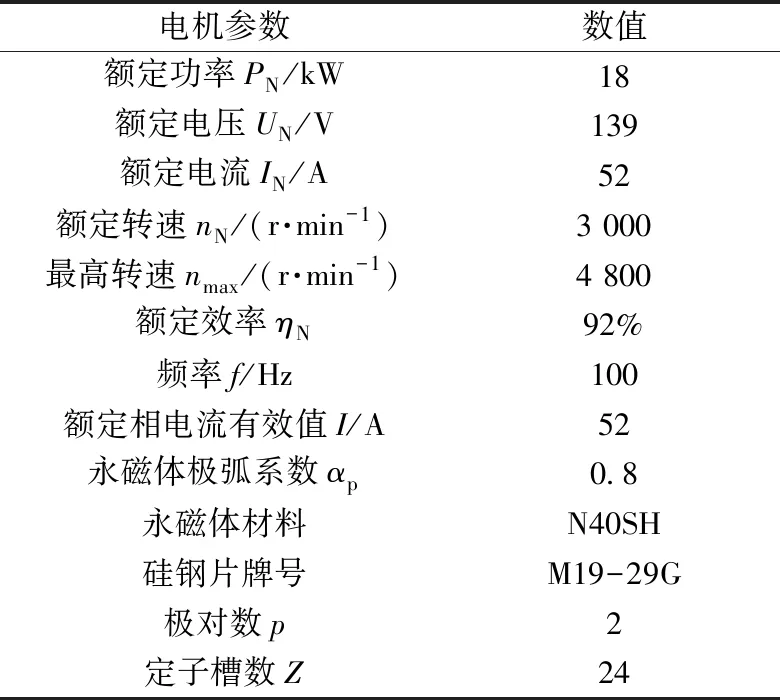
表1 電機參數

在計算定子鐵心損耗時，對于鐵心區域的不同位置，磁通密度的變化規律和幅值大小都不相同。根據有限元理論，需要將定子鐵心區域劃分為多個小區域進行計算，然后將每一個小區域的損耗相加得到定子鐵心總損耗。這種計算方法結果雖然精確，但是計算量非常龐大。為了簡化計算且得到較為精確的結果，將磁通密度幅值和變化規律相近的點整合為一個典型區域，用一點處的參數量對整個區域進行求解。

本文研究的表貼式永磁同步電機，將定子鐵心依據齒、軛部的不同位置分為齒頂、齒中、齒根以及定子軛部四部分。如圖6所示。

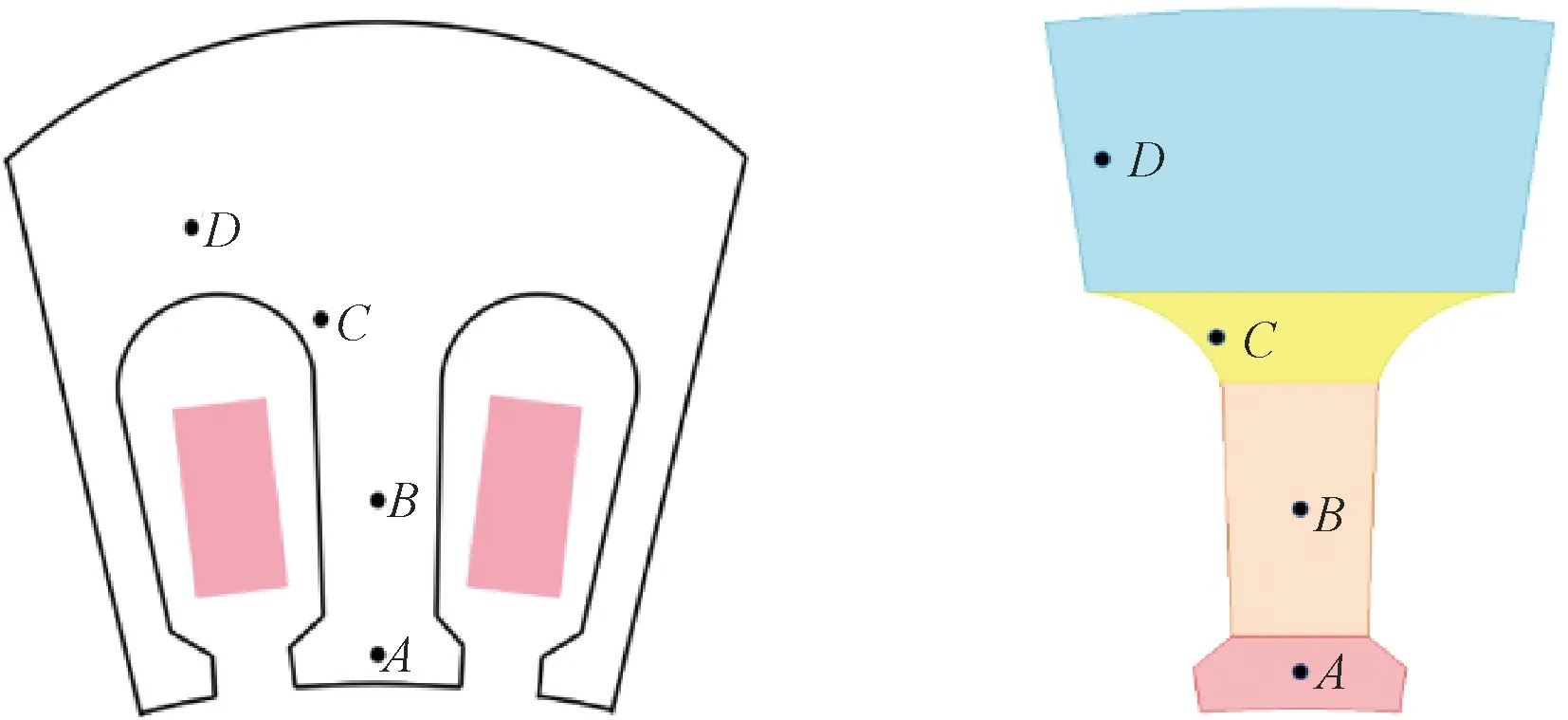
圖6 定子四個區域劃分

取A、B、C、D四點處的磁通密度為基值，利用三種不同的計算模型對定子鐵心損耗進行求解。第一種模型利用四點處的磁通密度幅值通過式(5)求解；第二種模型對四點處磁通密度進行正交分解后通過式(5)求解；第三種模型對四點處磁通密度進行正交分解并進行頻域分解后通過式(6)求解。三種模型的計算結果如表2所示。

表2 鐵心損耗計算結果對比

從表2中可以看出，直接利用四點處的磁通密度幅值求解鐵心損耗時，誤差較大；而采用四點處磁通密度正交分解并進行頻域分解后的數據進行求解時，誤差很小。

3 永磁體極弧系數優化分析

3.1 優化模型

永磁同步電機的許多結構參數變化時均會對電機電磁特性產生影響。提升電機的性能，需要選擇對電磁性能影響較大的結構參數進行優化。本文選取永磁體極弧系數作為優化變量，表貼式永磁同步電機的永磁體基本幾何尺寸如圖7所示。

圖7 永磁體基本幾何尺寸

永磁體極弧系數αp定義為極弧寬度與極距的比值，即：

(7)

式中：p為電機極對數；β為每極永磁體所跨弧度值。在優化設計時，設計變量、目標函數和約束條件三項缺一不可。

將定子鐵心損耗、永磁體體積與輸出轉矩峰峰值的權重函數作為目標函數；約束條件選擇感應電動勢小于0.9倍的額定相電壓，輸出轉矩與極弧系數為0.8時的額定轉矩相等。可以得到優化設計模型如下：

(8)

式中：a1、a2、a3分別為定子總損耗、永磁體體積與轉矩波動的權重系數；pcu為銅損；pFe為鐵心損耗；pFe+pcu為定子總損耗；VPM為永磁體體積；Tpk2pk為轉矩峰峰值；roc為定子總損耗、永磁體體積與輸出轉矩峰峰值的變化率；E0為感應電動勢；UN為額定相電壓有效值；Tαpi為極弧系數αpi時的輸出轉矩；T0.8為極弧系數取0.8時的輸出轉矩。

3.2 優化分析

本文對永磁體極弧系數αp進行參數化仿真，αp在0.6到0.86之間每隔0.02取值，共建立14個電機模型。通過二維有限元仿真計算得到電樞繞組銅耗隨永磁體極弧系數αp的變化曲線，如圖8所示；定子鐵心損耗隨永磁體極弧系數αp的變化曲線如圖9所示；定子部分總損耗隨永磁體極弧系數αp的變化曲線如圖10所示；輸出轉矩峰峰值隨永磁體極弧系數αp的變化曲線如圖11所示。

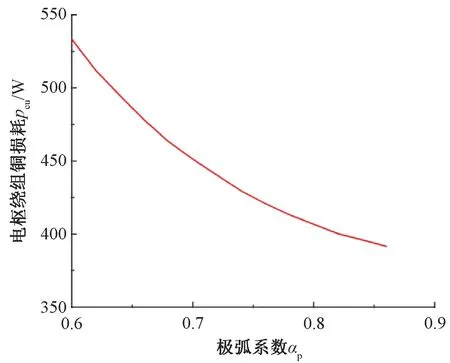
圖8 繞組銅耗隨極弧系數變化曲線

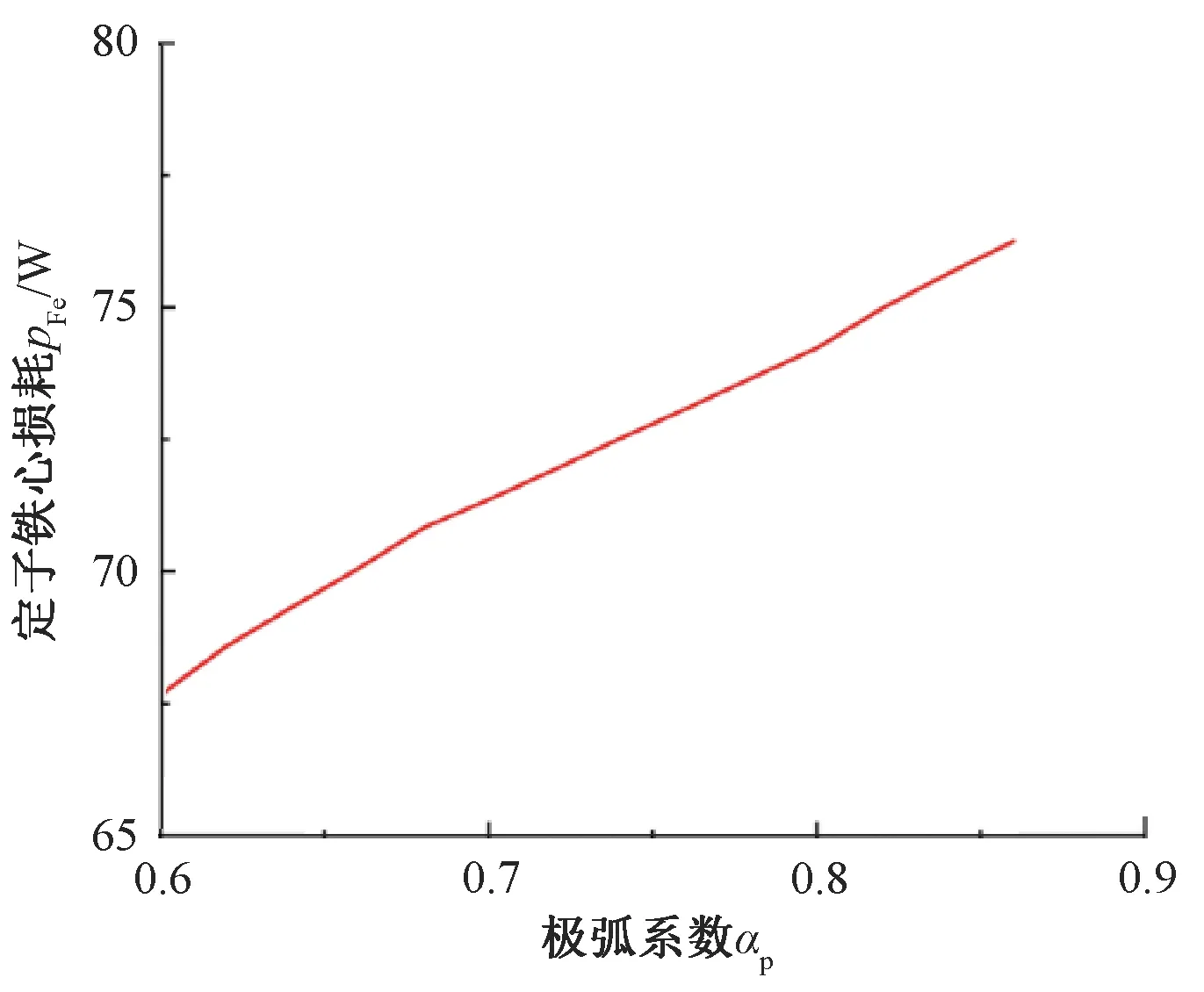
圖9 定子鐵損隨極弧系數變化曲線

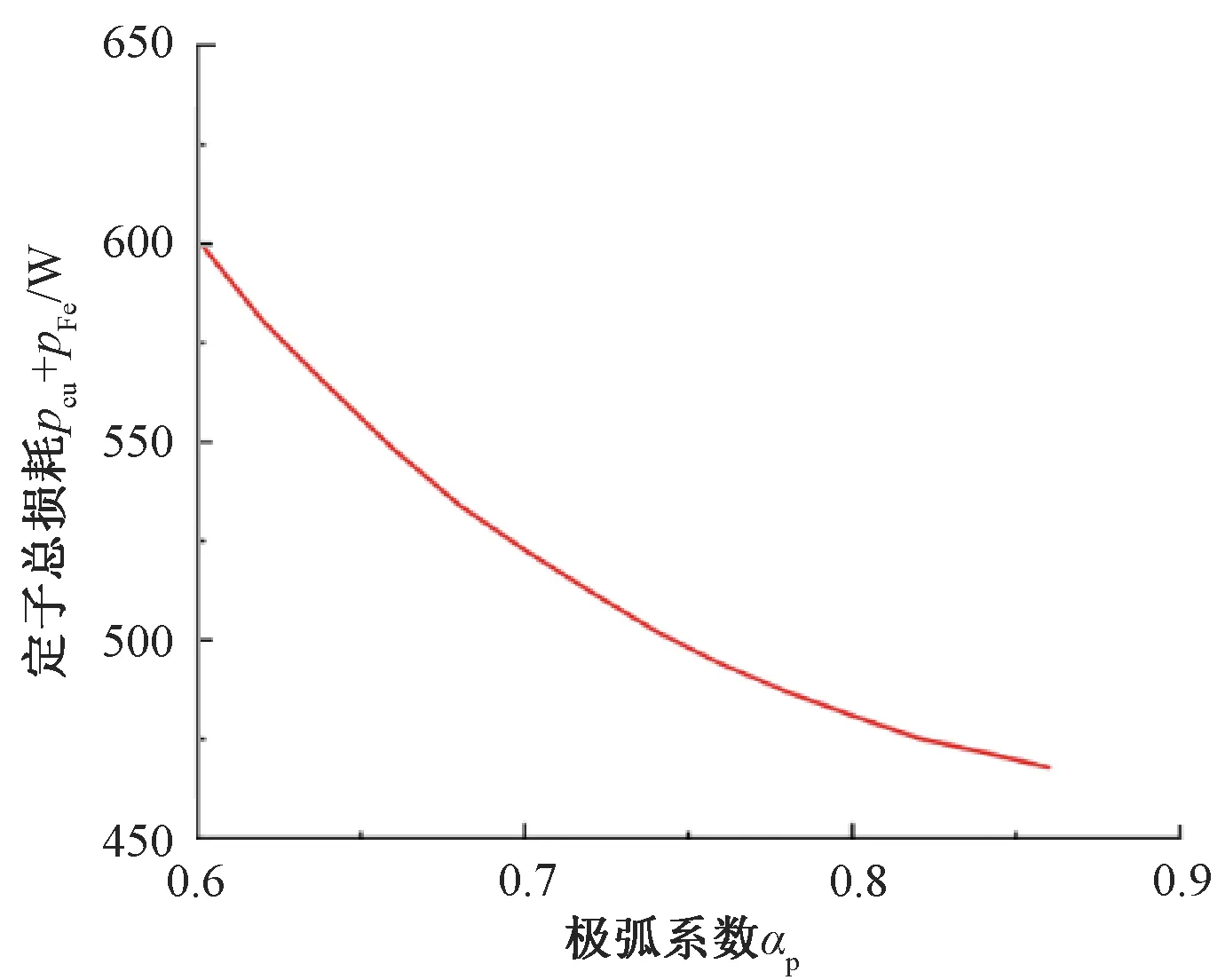
圖10 定子總損耗隨極弧系數變化曲線

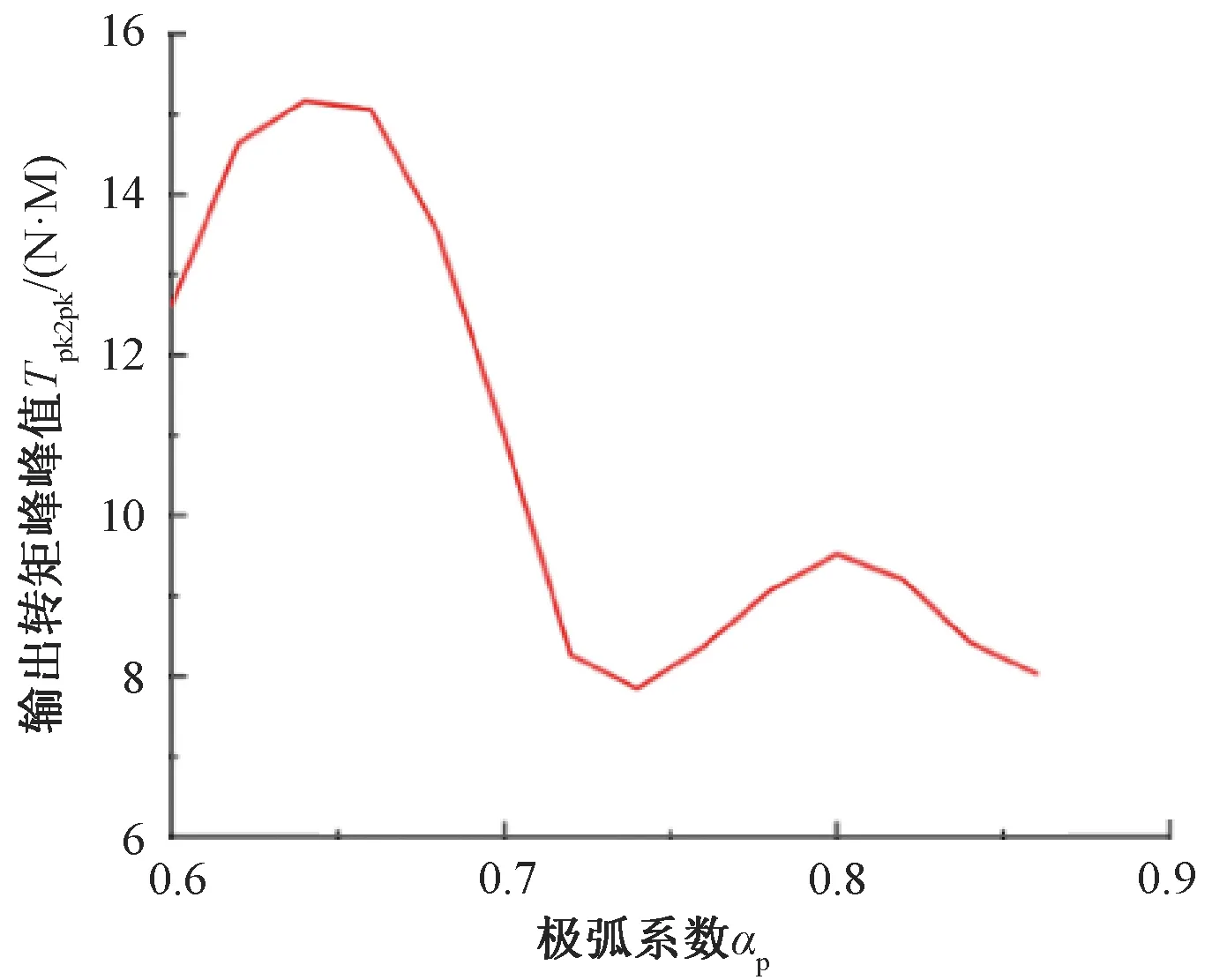
圖11 轉矩峰峰值隨極弧系數變化曲線

參數變化率計算公式：

(9)

式中：roc(Y)為參數Y的變化率；YRV為參數Y的基準值，基準值選取優化前的參數值，即極弧系數為0.8；Yi為極弧系數取αpi時的參數值。

各參數變化率隨永磁體極弧系數的變化曲線如圖12所示。

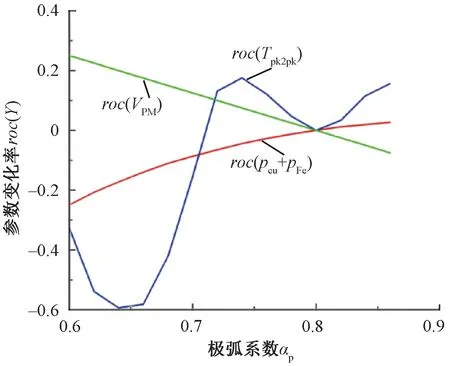
圖12 各參數變化率隨極弧系數變化曲線

權重系數矩陣A如下：

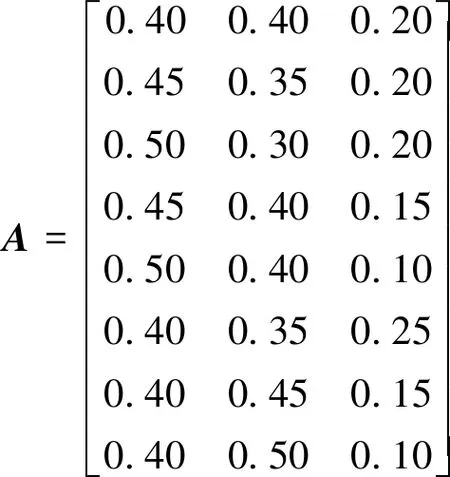
(10)

權重系數取不同值時，對應目標函數曲線如圖13所示。

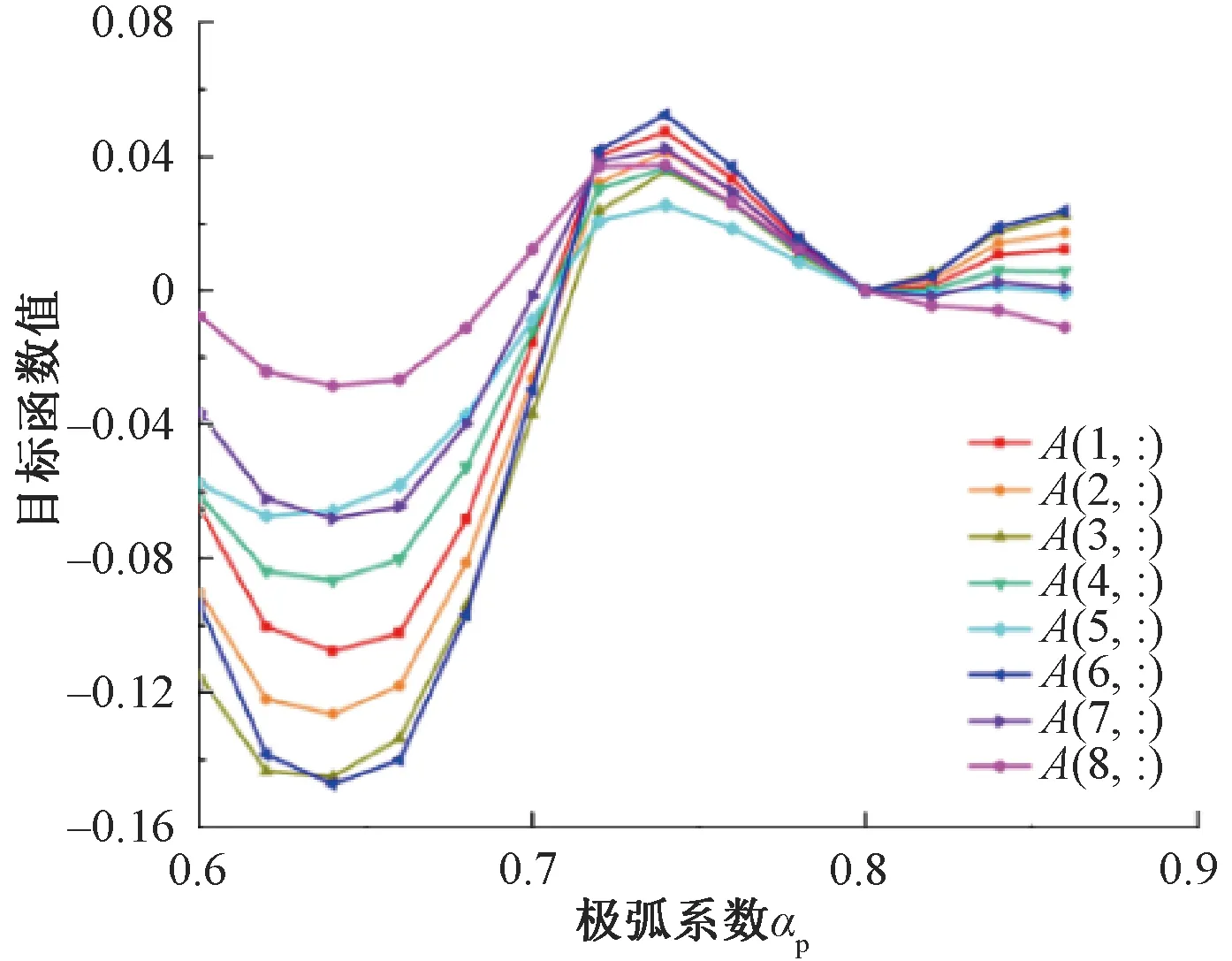
圖13 不同權重系數時目標函數曲線

從圖13可以看出，權重系數取不同值時，目標函數值變化比較大。權重系數取值A(1，：)～A(7，：)，極弧系數取值0.6～0.7時，目標函數值小于零，即優化后較優化前電機性能下降，極弧系數取值0.72～0.86時，目標函數值大于零，即優化后較優化前電機性能提高；權重系數取值為A(8，：)時，極弧系數取值0.6～0.68與0.82～0.86時，目標函數值小于零，即優化后較優化前電機性能下降；極弧系數取值0.7～0.78時，目標函數值大于零，即優化后較優化前電機性能提高；權重系數取不同值時，極弧系數為0.74時，目標函數均取最大值，即永磁體極弧系數取0.74時優化后電機性能最優。使用ANSYS EM電磁仿真軟件Toolkit模塊仿真計算得到電機全工作區域下的穩態效率圖，如圖14所示。在電機轉速3 000 r/min，相電流有效值52 A額定工況下的有限元仿真計算效率為94.81%。

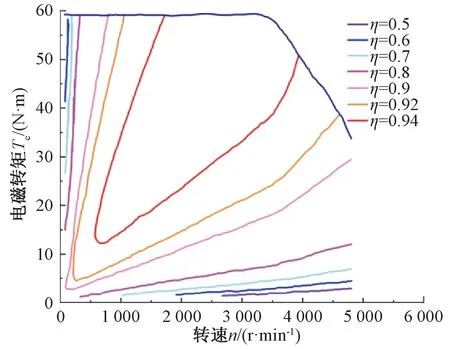
圖14 電機效率仿真

4 結 語

本文在考慮定子鐵心損耗的情況下，以輸出轉矩不變作為約束條件，以定子損耗、永磁體體積與輸出轉矩峰峰值綜合最優為目標函數，建立了永磁體極弧系數優化模型。

通過分析表貼式永磁同步電機的定子鐵心損耗，可以看到，采用考慮旋轉磁化和諧波的鐵心損耗計算模型相較于鐵耗分離模型，對定子鐵心損耗計算更加合理。

優化后永磁體極弧系數為0.74時，電機綜合性能最優。雖然定子部分總損耗較優化前有所增加，但優化后永磁體體積減小，輸出轉矩峰峰值也有所減小，電機綜合性能有所提高。

本文的研究可為今后永磁同步電機設計時永磁體極弧系數的選取提供參考。