基于機器人逆運動學(xué)的磨削姿態(tài)優(yōu)化方法＊

徐 源 尹緒偉 吳超群②

（①武漢理工大學(xué)機電工程學(xué)院，湖北 武漢 430070；②武漢理工大學(xué)硅酸鹽建筑材料國家重點實驗室，湖北 武漢 430070）

隨著機器人技術(shù)的發(fā)展，越來越多的機器人被用于鉆孔、切割和拋光等機械加工中。雖然在某些情況下，機器人加工可以以相對較低的成本執(zhí)行各種任務(wù)。然而由于機器人的剛度低于傳統(tǒng)CNC機床（傳統(tǒng)CNC機床剛度高于50 N/μm，而工業(yè)機器人剛度小于1 N/μm）[1]，機器人在加工過程中容易發(fā)生顫振，影響加工質(zhì)量。在假設(shè)機器人連桿剛性的情況下，機器人末端的加工剛度主要與機器人的關(guān)節(jié)剛度和姿態(tài)有關(guān)[2]。對于已經(jīng)具有成熟技術(shù)的工業(yè)機器人來說，改變它的關(guān)節(jié)剛度非常困難，但是，可以針對工業(yè)機器人的加工姿態(tài)進行優(yōu)化，提高機器人的加工剛度，得到更好的加工性能[3]。

針對機器人姿態(tài)優(yōu)化的問題，國內(nèi)外學(xué)者做了許多研究。Guo Y J[4]等通過研究機器人末端執(zhí)行器的位移與其受力的關(guān)系，得到一種評定給定姿態(tài)下機器人剛度的性能指標(biāo)。并根據(jù)這一性能指標(biāo)建立機器人姿態(tài)優(yōu)化模型，得到機器人在指定加工條件下的最優(yōu)姿態(tài)。Lin Y[5]等提出一種變形評估指標(biāo)來直接說明6R工業(yè)機器人末端執(zhí)行器在受力時的變形，并運用這一變形評估指標(biāo)獲得機器人加工變形圖確定末端執(zhí)行器的方向，獲得加工性能最佳的6R機器人姿態(tài)。但是，針對加工位置固定的工件，機器人末端的位置和方向是固定的，不能用上述方法優(yōu)化機器人的姿態(tài)，需要運用機器人逆運動學(xué)進行求解。針對這類問題，高威[6]等推導(dǎo)出一種基于正運動學(xué)的雅可比矩陣迭代數(shù)值求解法，并與傳統(tǒng)封閉求解法作比較，得到數(shù)值求解法更具有通用性，但其迭代過程復(fù)雜，運算時間較長。王見[7]等提出一種根據(jù)物體位置信息的6軸機器人姿態(tài)求解算法，并提出了一種服務(wù)球模型，得到機器人的姿態(tài)集合。上述求解算法存在多組逆解，多組逆解對應(yīng)的機器人姿態(tài)不同從而導(dǎo)致加工剛度的不同，需要對多組逆解進行分析，以選取加工剛度最優(yōu)的加工姿態(tài)。針對逆解的選取，肖志鍵[8]等根據(jù)解析表達式的數(shù)學(xué)特性和機器人運動的連續(xù)性得到一種逆解選取優(yōu)化算法，并用軟件仿真證明了算法的有效性。

通過對國內(nèi)外學(xué)者對工業(yè)機器人逆運動學(xué)求解方法的分析發(fā)現(xiàn)，針對末端位置固定的加工場景，運用逆運動學(xué)求解可更直觀地得到機器人的加工姿態(tài)，為求取操作剛度最優(yōu)的機器人加工姿態(tài)提供理論基礎(chǔ)。

本文提出了一種基于機器人逆運動學(xué)的磨削姿態(tài)優(yōu)化方法，首先根據(jù)機器人末端位置與方向，運用機器人逆運動學(xué)求解機器人加工姿態(tài)，通過給定的機器人剛度性能指標(biāo)評價求得的各種姿態(tài)，并從中選取最優(yōu)加工姿態(tài)配置，進一步考慮機器人末端加工冗余性，求解機器人的逆姿態(tài)，建立了考慮機器人末端加工冗余性的姿態(tài)優(yōu)化模型并得到了在給定加工條件下的優(yōu)化結(jié)果。最后采用有限元仿真驗證了該模型的正確性。

1 機器人磨削系統(tǒng)組成及運動學(xué)求解

1.1 機器人磨削系統(tǒng)

本文以鈦合金磨削為例，介紹了機器人加工系統(tǒng)的組成。如圖1所示，機器人磨削系統(tǒng)由工業(yè)機器人、底座、工件、旋轉(zhuǎn)工作臺與排屑機5部分組成。在本機器人加工系統(tǒng)中，機器人抓取安裝有磨頭或砂輪的電主軸對工件進行打磨。

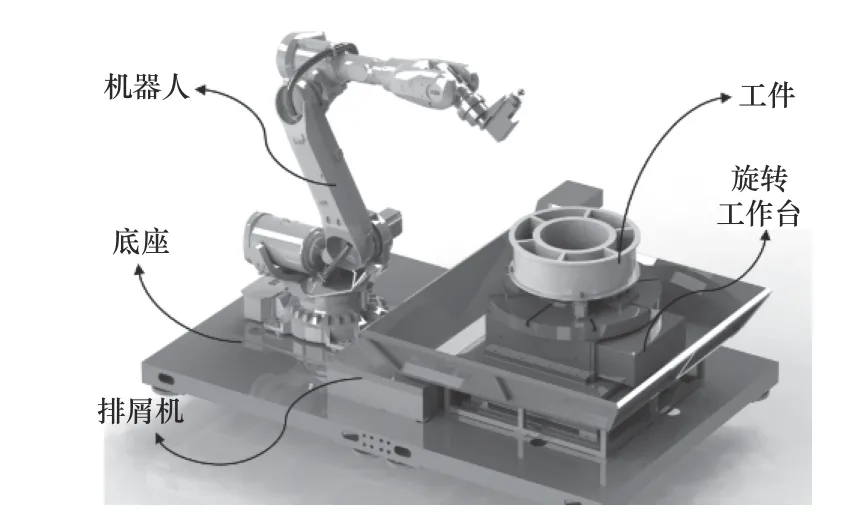
圖1 機器人磨削系統(tǒng)

1.2 IRB6700機器人的剛度模型

根據(jù)制造商的數(shù)據(jù)，本文將采用D-H方法建立IRB6700機器人連桿坐標(biāo)系[9]，如圖2所示。

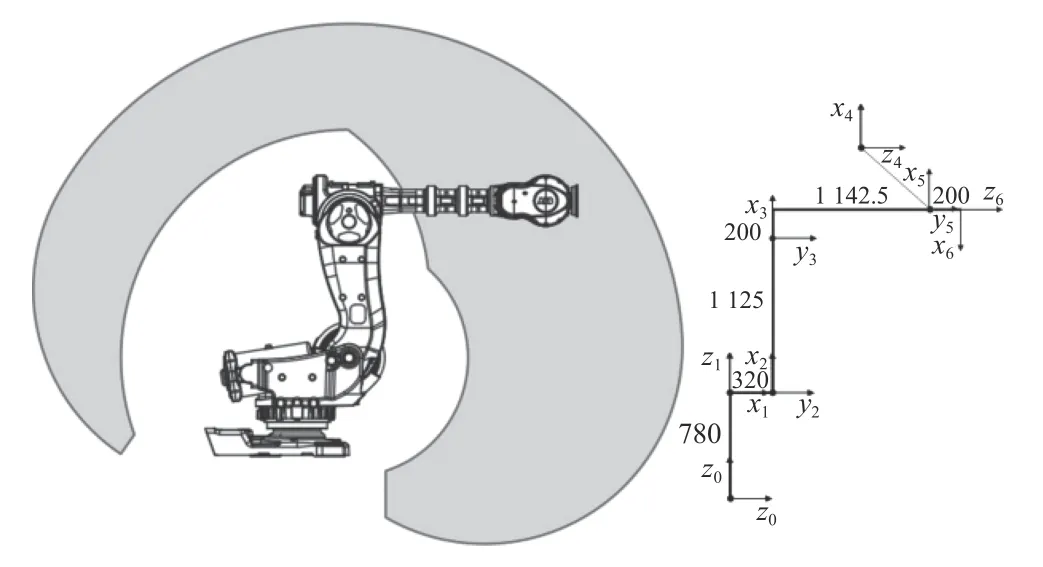
圖2 IRB6700機器人連桿坐標(biāo)系

根據(jù)機器人連桿參數(shù)（見表1）建立連桿坐標(biāo)系，并利用坐標(biāo)預(yù)位法得到機器人從坐標(biāo)系{i-1}到坐標(biāo)系{i}的變換矩陣[10]。得到連桿坐標(biāo)系之間的變換矩陣，如式（1）所示。

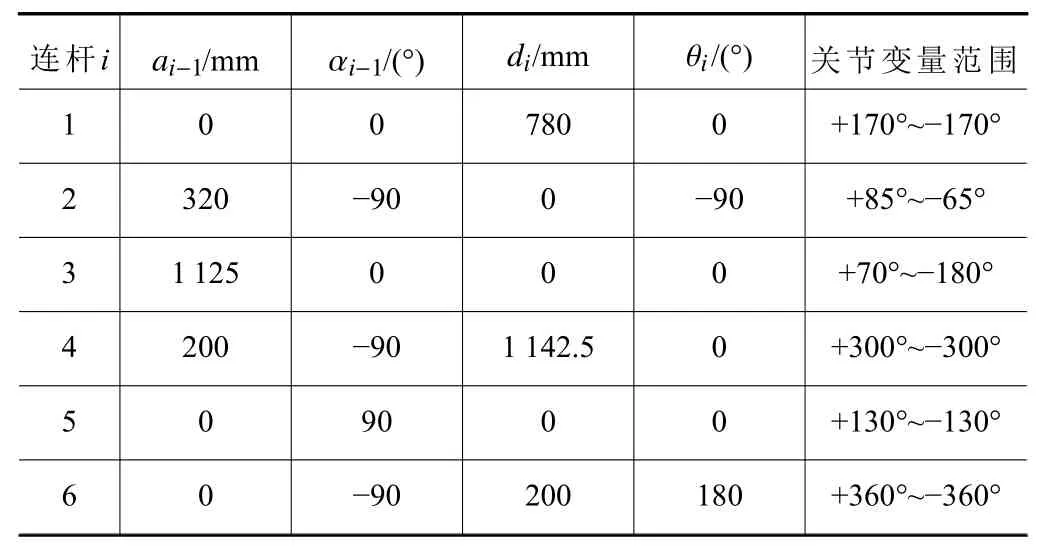
表1 IRB6700機器人連桿參數(shù)

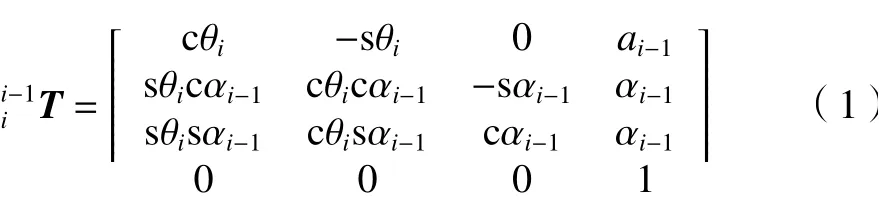
其中： s=sin ， c =cos。

將機器人各關(guān)節(jié)的變換矩陣相乘，得到第六軸坐標(biāo)系相對于基坐標(biāo)系的位姿矩陣

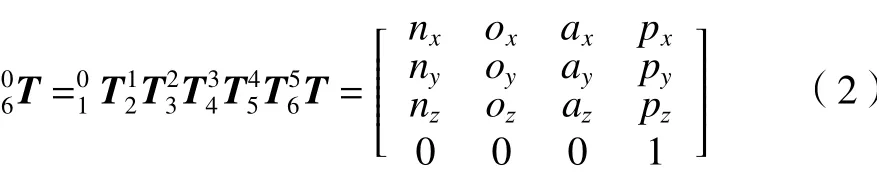
對于本文提出的工業(yè)機器人，機器人連桿的剛度遠(yuǎn)大于關(guān)節(jié)的剛度。由關(guān)節(jié)柔性引起的機器人末端變形遠(yuǎn)大于由連桿柔性引起的機器人末端變形[11]。因此，在忽略機器人連桿撓度的前提下，考慮機器人的關(guān)節(jié)撓度，建立機器人的靜態(tài)剛度模型。

式中：F是機器人末端受到的力；X是機器人末端受力以后產(chǎn)生的變形；Kq是機器人關(guān)節(jié)剛度矩陣J是機器人雅可比矩陣，用來描述機器人笛卡爾關(guān)節(jié)速度與笛卡爾空間速度之間的關(guān)系，可通過微分；變換法得到。

式（3）變換得式（4）。

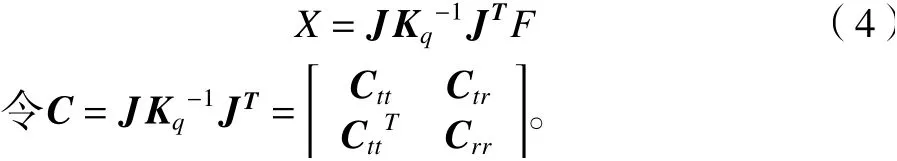
式中：C是6×6的柔度矩陣。Ctt為3×3階平移柔度子矩陣，Crr為3×3階旋轉(zhuǎn)柔度子矩陣。Ctr為3×3階耦合柔度子矩陣。

在實際加工應(yīng)用中，由力矩產(chǎn)生的旋轉(zhuǎn)變形很小，可以忽略不計，主要考慮的是由力引起的平移變形。故為了簡化問題，本文主要討論機器人末端執(zhí)行器受力與位移之間的關(guān)系。方程式可表示為

由于機器人末端剛度具有各向異性，為評價機器人的操作剛度增加了難度。故本文參考的文獻[4]提出的機器人剛度性能指標(biāo)，如式 （5） 所示。對于任意機器人姿態(tài)，ks越大，機器人整體剛度性能越好。本文利用該指標(biāo)來評價機器人在不同姿態(tài)下的剛度。

1.3 IRB6700機器人的逆運動學(xué)

對于工業(yè)機器人，當(dāng)關(guān)節(jié)角配置已知時，其第六軸坐標(biāo)系的位置和姿態(tài)是確定的。當(dāng)機器人第六軸坐標(biāo)系的位置和姿態(tài)已知時，求解機器人關(guān)節(jié)角配置是一個逆運動學(xué)問題。

本文中機器人的逆運動學(xué)采用分離變量法求解。已知條件是06T，解是機器人每個關(guān)節(jié)的角度。式（7）是通過將式（2）左乘和 右乘得到的。

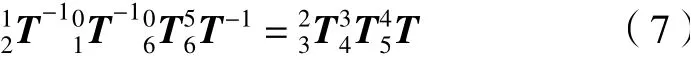
分離變量θ1， 通過式（8）得到 θ1的值。

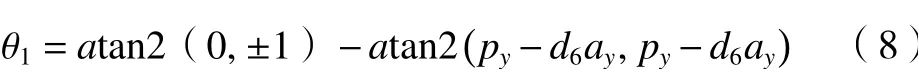
以同樣的方式，在等式（2）兩邊同時乘以對應(yīng)的矩陣，并分離解變量得到 θ2, ···, θ6的結(jié)果。

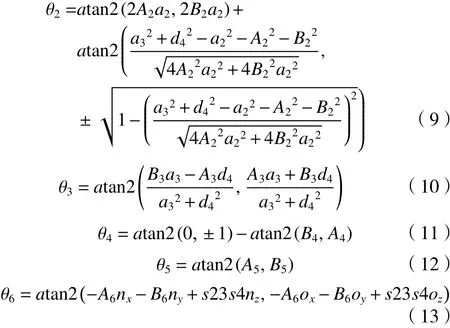
觀察機器人6個關(guān)節(jié)的解方程，發(fā)現(xiàn)關(guān)節(jié)1、2、4最多存在兩個逆解，分別對應(yīng)于機器人8組不同的逆解。

對于任意給定的末端姿態(tài)矩陣，由于機器人結(jié)構(gòu)和關(guān)節(jié)角度的限制，逆解不一定存在，因此需要判斷機器人姿態(tài)可達性。觀察機器人的逆運動學(xué)方程，發(fā)現(xiàn)求解關(guān)節(jié)2時可能沒有解。當(dāng)關(guān)節(jié)2的逆解不存在時，機器人不可達。當(dāng)機器人關(guān)節(jié)2的逆解存在，并且關(guān)節(jié)1到關(guān)節(jié)6的求解值在機器人關(guān)節(jié)的變量范圍內(nèi)時，姿態(tài)是可達的。以上篩選原理如圖3所示。

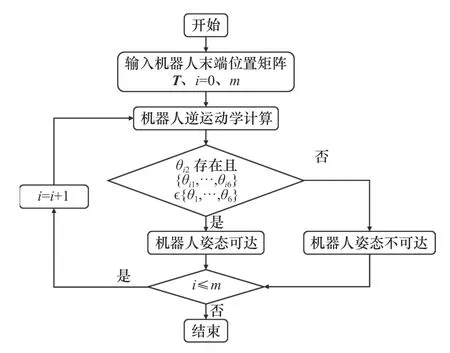
圖3 機器人姿態(tài)可達性判斷流程圖

2 機器人姿態(tài)優(yōu)化模型的建立及求解

2.1 磨削機器人的加工姿態(tài)

圖4是機器人加工的示意圖。在確定刀具位置和姿態(tài)的同時，也確定了機器人第六軸坐標(biāo)系的位置和姿態(tài)。通過逆運動學(xué)，可以得到這類機器人的不同逆解。圖5展示出了機器人的某個加工點的4個逆姿態(tài)，表2給出了對應(yīng)于機器人的4組不同的關(guān)節(jié)角度配置。

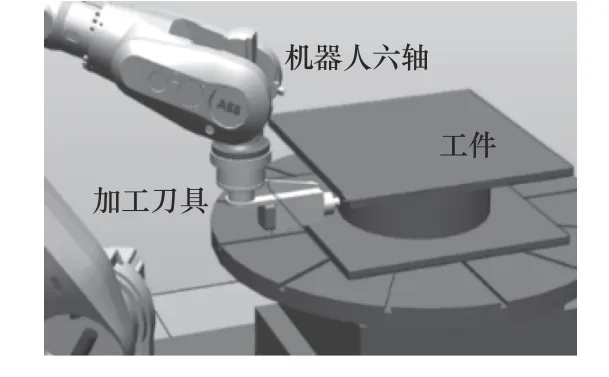
圖4 機器人磨削示意圖

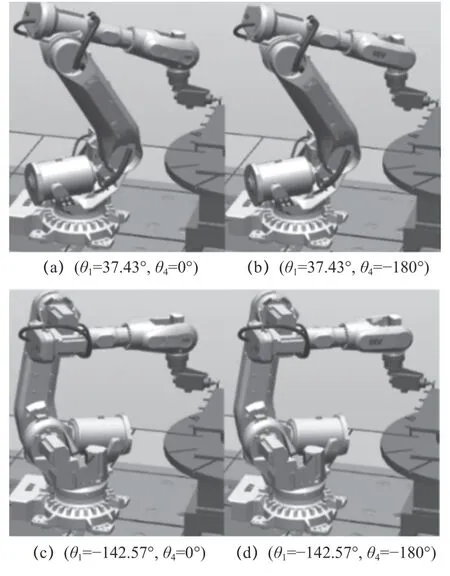
圖5 機器人磨削的4種逆姿態(tài)

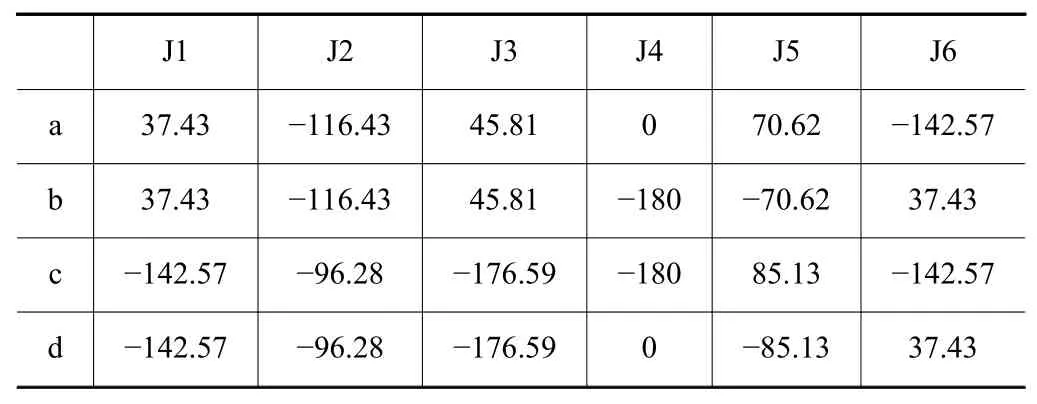
表2 機器人的4個逆姿態(tài)參數(shù)

計算對應(yīng)于上述4個逆姿態(tài)下的機器人末端加工剛度。對應(yīng)于姿態(tài)a和b的剛度性能指數(shù)ks為7.226 3，對應(yīng)于姿態(tài)c和d的剛度性能指數(shù)ks為4.322 7。對前兩個姿勢和后兩個姿勢分別進行了分析。姿態(tài)a和b對應(yīng)的剛度性能優(yōu)于姿態(tài)c和d，剛度性能指標(biāo)相差67%。發(fā)現(xiàn)機器人不同逆姿態(tài)對應(yīng)的加工剛度差異較大。在實際加工過程中，我們可以選擇一個最優(yōu)的逆解姿態(tài)。上述機器人姿態(tài)逆運動學(xué)優(yōu)化模型如下：

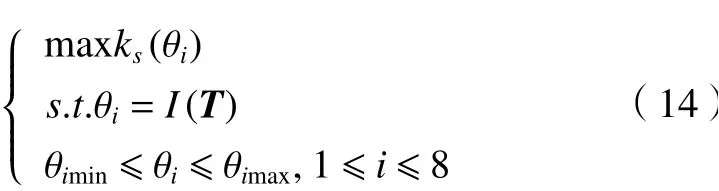
式中： θi是 由機器人末端位置矩陣T通過逆運動學(xué)求解得到的機器人關(guān)節(jié)配置。機器人姿態(tài)逆運動學(xué)優(yōu)化流程圖如圖6所示。

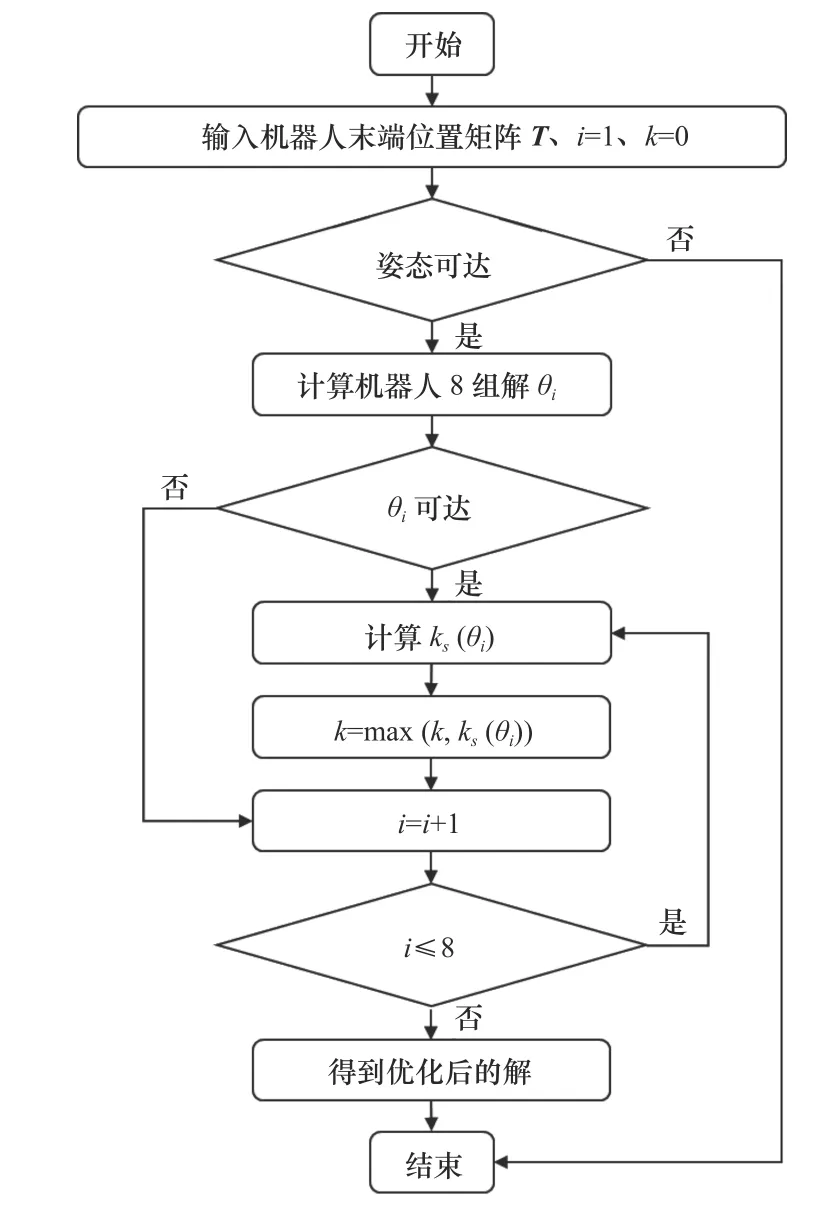
圖6 機器人姿態(tài)逆運動學(xué)優(yōu)化流程圖

2.2 考慮加工冗余的機器人姿態(tài)優(yōu)化模型的建立

機器人抓取刀具加工工件時，旋轉(zhuǎn)刀具相當(dāng)于一個自由度，6自由度機器人出現(xiàn)加工冗余。該冗余自由度是機器人圍繞工具軸向的旋轉(zhuǎn)。基于冗余自由度，機器人的姿態(tài)可以進一步優(yōu)化，使剛度性能指標(biāo)最大化。首先，選擇機器人的初始加工姿態(tài)，利用機器人姿態(tài)逆運動學(xué)優(yōu)化模型獲得最優(yōu)逆姿態(tài)，并計算該姿態(tài)下機器人操縱剛度的性能指標(biāo)。其次，機器人圍繞刀具軸以給定的角度旋轉(zhuǎn)。如果機器人的姿態(tài)是可達的，則利用機器人的逆姿態(tài)優(yōu)化模型得到旋轉(zhuǎn)后的最優(yōu)逆姿態(tài)。計算機器人在該姿態(tài)下的剛度性能指標(biāo)，并與之前的最優(yōu)逆姿態(tài)進行比較，更新最優(yōu)姿態(tài)。如果機器人旋轉(zhuǎn)后姿態(tài)不可達，則跳過旋轉(zhuǎn)角度，在下一個角度計算，直到機器人旋轉(zhuǎn)到初始姿態(tài)。通過以上步驟，最終得到機器人的最優(yōu)加工姿態(tài)，優(yōu)化模型為

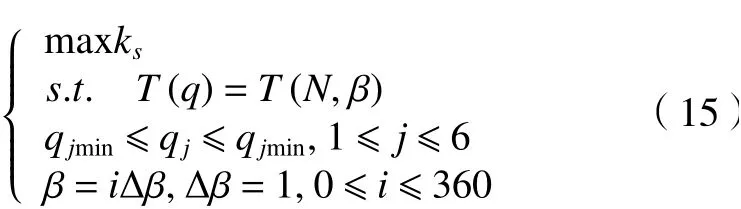
式中：ks為 機器人剛度性能指標(biāo)，T(q)是由機器人初始姿態(tài)N與工具軸旋轉(zhuǎn)角度 β推導(dǎo)出的機器人末端姿態(tài)。推導(dǎo)出的機器人末端姿態(tài)。考慮加工冗余的機器人姿態(tài)優(yōu)化流程圖如圖7所示。

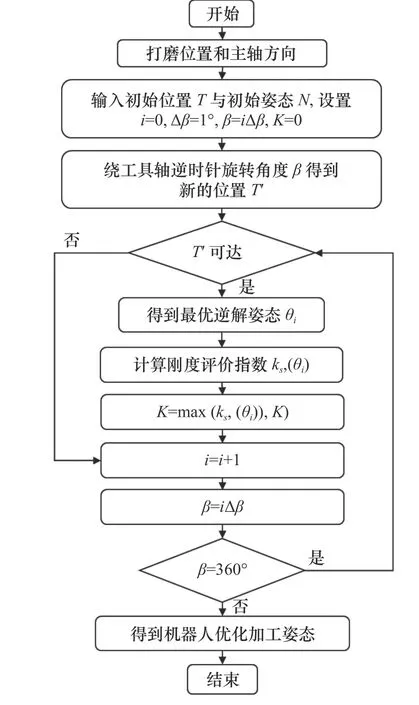
圖7 考慮加工冗余的機器人姿態(tài)優(yōu)化流程圖

2.3 優(yōu)化結(jié)果的仿真分析

選擇加工點，基于建立的姿態(tài)優(yōu)化模型，在Matlab軟件中編程得到最佳加工姿態(tài)，機器人姿態(tài)優(yōu)化結(jié)果如圖8所示。

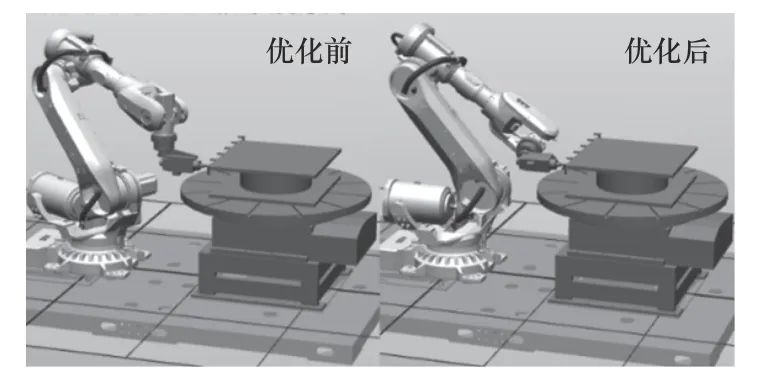
圖8 機器人優(yōu)化前后加工姿態(tài)

圖8左側(cè)是機器人的初始加工姿態(tài)，右側(cè)是優(yōu)化后的加工姿態(tài)。將上述兩種機器人姿態(tài)導(dǎo)入有限元分析軟件中仿真分析機器人的受力變形。

在仿真軟件中對機器人模型進行如下處理：

（1）為防止網(wǎng)格劃分復(fù)雜，減少仿真分析任務(wù)量，對模型上影響不大的連接孔、倒角、圓角等結(jié)構(gòu)進行簡化處理，對氣缸等物件進行等配重簡化處理。

（2）機器人材料設(shè)置為結(jié)構(gòu)鋼。

（3）選用bonded約束定義機器人關(guān)節(jié)之間的連接。

（4）將機器人底座設(shè)置為固定支撐。

（5）選擇四面體網(wǎng)格劃分。

（6）在機器人法蘭盤末端分別施加豎直向下及水平的載荷力以模仿機器人在打磨過程中的實際工況，載荷力的大小為 1000N。受力示意圖如圖9～11所示。分析結(jié)果如圖12所示。

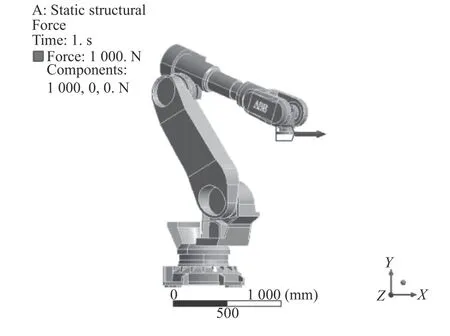
圖9 姿態(tài)優(yōu)化前機器人在X方向上受力與仿真

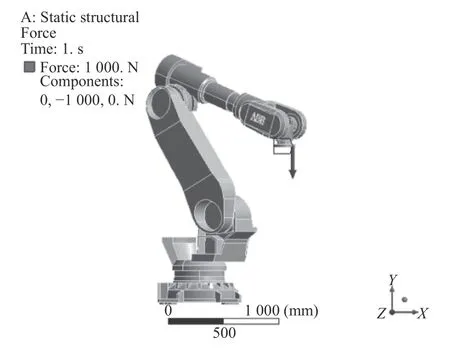
圖10 姿態(tài)優(yōu)化前機器人在Y方向上受力與仿真

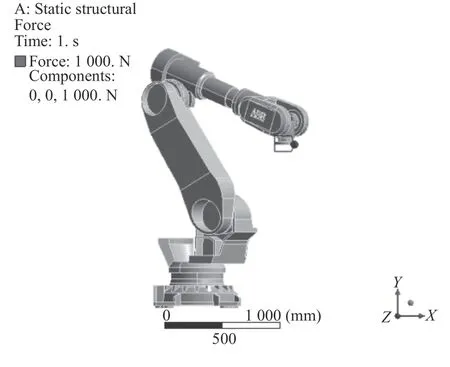
圖11 姿態(tài)優(yōu)化前機器人在Z方向上受力與仿真

圖12 機器人在3個方向上優(yōu)化前后仿真分析結(jié)果

從圖12中可以發(fā)現(xiàn)，在機器人末端X、Y、Z這3個方向分別施加 1000N的負(fù)載，得到機器人末端變形量。其中，優(yōu)化前機器人在3個方向上的末端最大變形量分別為0.119 88 mm、0.151 57 mm和0.290 83 mm，優(yōu)化后機器人在3個方向的末端最大變形量分別為0.109 76 mm、0.109 48 mm和0.236 49 mm，3個方向的最大變形量分別降低了8.44%、27.77%和18.68%，說明優(yōu)化后的機器人末端加工剛度有所提高，且在3個方向上的優(yōu)化效果各不相同，其中在Y方向上的提升效果最為明顯，為27.77%。采用上述方法可以提高機器人的加工剛度。

3 結(jié)語

本文針對工業(yè)機器人加工剛度弱的問題，選用了基于機器人逆運動學(xué)的機器人加工姿態(tài)求解方法，得到機器人最優(yōu)加工姿態(tài)。根據(jù)以上研究，本文主要得到以下結(jié)論：

（1）通過逆運動學(xué)求得機器人姿態(tài)隨著關(guān)節(jié)角度配置的不同，加工剛度存在差異，不同姿態(tài)下機器人剛度性能指標(biāo)相差可達67%。

（2）考慮到加工冗余度，可進一步優(yōu)化機器人的加工剛度，優(yōu)化前后機器人在3個方向的最大變形量均有所降低，其中在Y方向效果最為顯著，最大變形量降低了27.77%。