基于改進A＊算法的AGV轉運機器人路徑規劃研究

石英托 陳 華 張連新 孫鵬飛 裴 培 李代楊

（中國工程物理研究院機械制造工藝研究所，四川 綿陽 621900）

隨著科學技術的發展，智能存儲等手段層出不窮，如AGV全向車等實現我國舟山港的無人化，南京晨光集團裝配過程中各工位間智能轉運等。機器人正逐步替代人工，成為自動化生產與運輸領域的生力軍。在執行某些轉運任務時，需要操作人員完成某些特定工序，與機器人共享工作空間。由于人的誤操作、機器人故障等意外，機器人可能會與人發生碰撞，對人員的安全產生威脅。因此如何保證人與機器人的安全交互是AGV機器人廣泛應用于自動化運輸需首要關注的問題。

機器人路徑規劃提供了一種解決方案。路徑規劃包含兩個層次，一是避障，控制機器人能自主避開障礙物；二是最優，按照需求規劃出路徑最短或耗費最少的路徑。國內外常用的路徑規劃算法包括Dijkstra算法[1]、A*算法[2]、動態規劃算法[3]、遺傳算法[4-5]和人工勢場法[6]等。Geetha S等[7]將蟻群算法與遺傳算法相結合，在多目標路徑規劃中得到了很好的效果；王志中等[8]提出了基于改進粒子群算法的機器人路徑規劃方法，改進算法規劃的路徑在長度、平滑度和規劃時間上均具有優勢。相比其他算法，A*算法簡單，易實現，便于機器人避碰路徑規劃，但在障礙較多、環境復雜的情況下計算迭代次數較多，影響其計算的實時性。

本文的研究基于筆者單位在研的某產品高效裝配生產線項目，旨在提出一種改進的A*路徑規劃算法，應用于AGV轉運機器人運動控制中，當檢測到運動路線上出現障礙物后，能夠實時規劃運動路徑，實現AGV機器人主動避碰，從而在不影響轉運效率的前提下，提高AGV機器人應用的安全性。其主體架構為：首先對AGV機器人和運動障礙進行分析，建立機器人運動交互環境模型；隨后對傳統A*算法進行分析，提出一種改進的A*路徑規劃算法；接著對改進后的算法進行Matlab仿真驗證；最后對文章進行總結。

1 環境建模

圖1為某產品高效裝配生產線分配了裝配、倉儲等區域。為節省人力，提高轉運效率，不同區域間產品及工裝的轉運就依靠AGV轉運機器人實現。

圖1 高效裝配生產線示意圖

AGV轉運機器人上裝有導航模塊，能夠對運動環境進行實時掃描，通過控制器計算與處理，將環境信息轉化為計算機可識別的數據，進而建立AGV運動交互環境模型。

基于環境信息的建模方法有很多，常用的有拓撲圖法、柵格法和導航網絡[9]等。本文采用柵格法進行環境建模，其優勢在于：

（1）利用規則長方形包絡障礙物來近似建模，雖然擴大了障礙域，所規劃的路徑并非最短無碰撞路徑，但實則增大了安全距離，提高了安全性。

（2）柵格法對隨機障礙域的表述準確，不易產生失真等情況，適用于現場復雜環境描述。

（3）柵格法對障礙域的描述相對簡化，從而提高路徑規劃的效率。

AGV機器人在廠區內工作環境相對復雜，運動路徑上可能出現雜物、操作人員等。AGV導航模塊對這些障礙進行實時掃描與識別，將其外形、位置等信息反饋給主控模塊用于構建環境模型。

基于上述分析，得到AGV機器人運動交互環境建模如圖2所示。其中1（左）為起點，2（右）為終點，黑色部分包含環境障礙和邊界，同視為障礙。

圖2 AGV機器人運動交互環境建模

2 路徑規劃算法研究

2.1 A＊算法原理

A*算法是廣泛用于尋路和圖遍歷的計算機算法，由于其具有較好的性能和準確性，經常被使用在最短路徑求解中，是一種啟發式搜索算法。其成本估計函數為

式中：f(n)代表從起始節點經由當前節點n到目標節點的成本估計，g(n)代表從初始節點到當前節點n的實際成本，h(n)代表從當前節點n到目標節點的最佳路徑的估計成本。

A*算法步驟為：

（1）將起點S加到OPEN表中。

（2）判斷OPEN表是否為空，若為空，則算法結束，無法找到路徑，否則進入下一步。

（3）從OPEN表中找到f(n)最小的節點N，添加到CLOSE表中，并判斷該節點是否為目標節點E，若為目標節點E，算法結束，否則進入下一步。

（4）找到節點N的所有相鄰節點Xi（i≤k，k為與節點N相鄰的全部節點個數）。若Xi不在OPEN表中也不在CLOSE表中，計算f(Xi)并加入OPEN表中；若Xi在OPEN表中，但是f(Xi)比OPEN表中估計值小，更新OPEN表中的估計值，并按從小到大排序；若Xi在CLOSE表中，則忽略該點。

（5）重復步驟2到步驟4，直到目標點E在CLOSE表中，表明已找到最優路徑，或OPEN表為空，算法結束。

在運行此算法之后，目標節點將指向其前導節點，依此類推，直到某個節點的前導是開始節點，就可以得到最短路徑序列。

區別于Dijkstra算法，A*算法用了一個啟發函數h(n)，使算法利用啟發信息朝著某個確定的方向搜索，所以其訪問的節點比Dijkstra算法少得多，能快速地導向目標結點，訪問到目標節點后算法停止。

2.2 A＊算法不足

A*算法原理簡單，使用靈活，因此在現代路徑規劃領域應用廣泛。但通過對其計算過程的分析，可知其存在一定的不足：朝著某個確定的方向搜索，能快速地導向目標結點。h(n)越小，A*算法需要擴展的點越多，運行速度越

（1）啟發函數的選取對算法的影響。啟發函數可以影響A*算法的運行，使算法利用啟發信息慢，此時算法運行效率較低；h(n)選取過大時，算法不一定能找到最佳路徑，運行質量較差。

（2）OPEN表對存儲空間的占用。當地圖較大、路徑較為發展時，OPEN表中會保存大量待考察的點，對存儲空間大量占用，使算法在表中插入、排序等操作變慢，影響運算效率。

（3）OPEN表中對成本估計f(n)的排序運算。隨著算法深入，OPEN表中節點數持續增加，每次迭代運算都要對表中各節點f(n)進行計算和排序，導致運算效率下降。

2.3 A＊算法改進

結合2.2小節對A*算法不足的分析，提出對A*算法進行改進。

2.3.1 啟發函數h(n)的選取

在A*算法的估價函數中，節點的g(n)值是實際值，而其h(n)值 是估值，h(n)選擇得越合理，那么f(n)的值就越接近真實值，A*算法的效率就會越高。實際計算時常采用曼哈頓距離、對角線距離和歐幾里得距離等[10-11]作為啟發函數。曼哈頓距離代表標準坐標系上絕對軸距總和；對角線距離相比曼哈頓距離，考慮了沿對角線移動的情況；歐幾里得距離特點是“兩點一線”，為兩點之間的最短距離。圖3可以對3種距離進行清晰地表述：

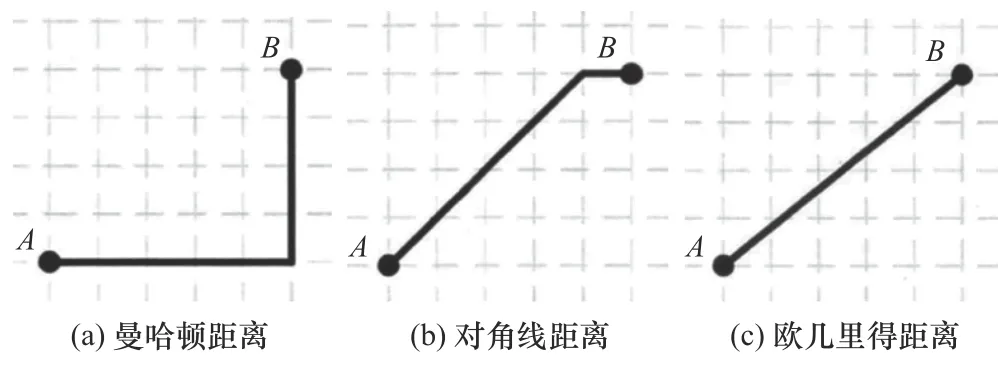
圖3 3種距離示意圖

圖中A為起點，B為終點，黑色實線為各自距離。對比3種距離，曼哈頓距離運算簡單，尋徑的效率高，但尋徑的質量較低；歐幾里德距離最短，易求得最短路徑，但計算涉及平方和開方運算，求解效率低；對角線距離作為啟發函數，在進行估值運算時與最優路徑的估值誤差不大，同時計算相對簡化，因此本文采用對角線距離啟發函數。具體計算過程如下：

式中：c表示在地圖中水平或豎直移動一步的代價，按對角線移動的代價則為由式（2）～（4）即可計算得到對角線距離的代價估值 。

2.3.2 OPEN表中節點數目優化管理

在A*算法進行路徑搜索過程中，每向目標方向擴展一次節點，就要對相鄰點f(n)進行計算，并在OPEN表中進行排序，導致算法擴展速度越來越慢。而實際上一些早期加入的和估值很大的節點就因不再需要而成為計算負擔。基于此，本文提出對OPEN表中節點數量進行管理與優化。當OPEN表中的節點數達到一定值時，刪除最早加入的估值較大的節點，使算法在后續運行過程中，OPEN表中節點數量維持恒定，這樣就提高了算法運行后期的計算效率。

對OPEN表中節點數量進行優化管理后，在同樣的條件下進行對比發現，運算效率得到了提高，同時擴展的節點并沒有減少，因此仍能夠得到與原算法相同的路徑搜索結果。

3 仿真驗證

改進A*算法在路徑搜索中的效果需要通過試驗進行驗證。本文中擬在Matlab環境中進行驗證。

仿真試驗的軟硬件環境如下：

軟件：Windows 7旗艦版 64位，Matlab R2015b（x86）；

硬件：CPU Intel Core i5-7500@ 3.40 GHz，內存8 G。

仿真實驗采用20×20方格，網格間隔0.2 m的區域進行，建立的環境模型如圖2所示。隨后分別對無障礙和不同障礙情況下算法的路徑規劃效果進行仿真驗證。仿真結果如圖4所示：

圖4 不同環境路徑規劃結果

路徑規劃結果中，網格變淺灰表示每次迭代運算過程中，該點被加入了OPEN表中，網格變深灰表示該點為淺灰點的相鄰待考察點；最終形成的黑色細線路線即為路徑搜索結果。

下面對路徑搜索效率進行比較，結果如表1所示。通過對仿真試驗結果進行分析，可以得出：

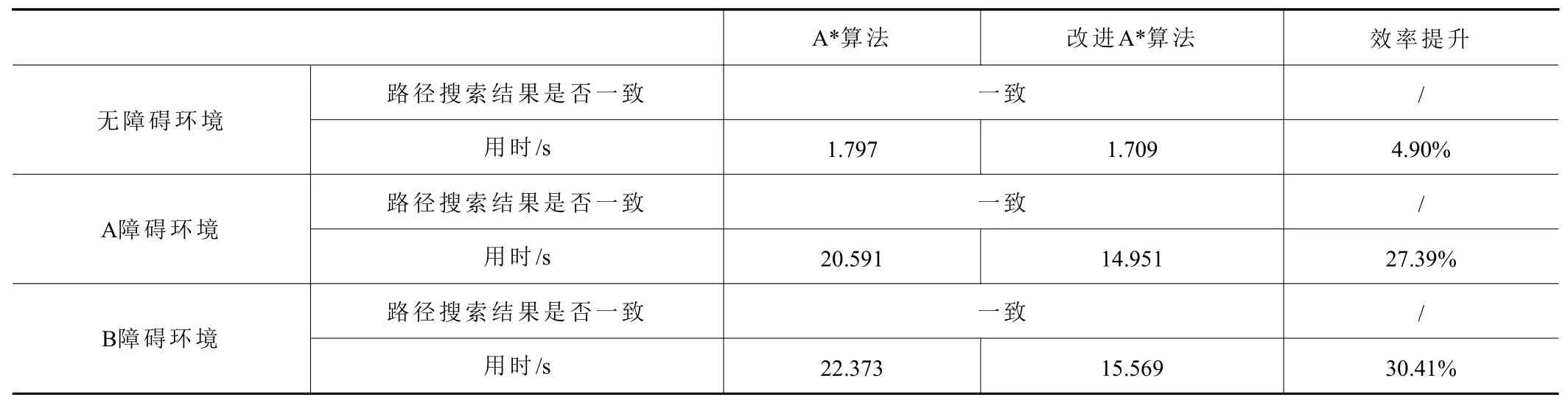
表1 路徑規劃效率比較

（1）改進A*算法與A*算法路徑規劃結果一致，都能利用啟發信息，朝著目標節點方向進行路徑搜索，從而快速導向至目標節點，同時都能夠規避障礙，規劃出合理路線。

（2）在路徑規劃效率方面。當環境較為簡單，運動路線上沒有障礙時，所規劃的運動路徑較為簡單，OPEN表中數量較少，算法改進后效率提升不明顯；當環境較為復雜，運動路線上出現障礙時，在路徑規劃迭代運算過程中，OPEN表中數量逐漸增加，算法改進后效率提升較為明顯；且當運動路線上障礙越復雜時，算法改進后效率提升更加明顯。

4 結語

本文針對提高AGV轉運機器人在高效裝配生產線項目應用中的安全性，提出了一種改進A*路徑規劃算法，應用于機器人運動控制中，能夠在不影響轉運效率的前提下，實現機器人主動避碰。通過仿真試驗，得出改進A*算法與A*算法路徑規劃一致，都能利用啟發信息，快速導向至目標節點；算法改進后，路徑規劃效率得到提升，且當運動路線上障礙越復雜，效率提升越明顯。因此，可認為改進A*算法能夠規劃路線，實現AGV機器人主動避障。