基于改進FMECA的洗衣機滾筒裝配線可靠性研究＊

白 穎 姚 琪

（①常州機電職業技術學院，江蘇 常州213164；②河海大學機電工程學院，江蘇 常州 213022）

隨著工業自動化的水平逐步加深，非標自動化行業逐漸興起，各種非標定制的生產裝配設備被廣泛應用于工廠當中[1]。但非標自動化設備往往設計周期短，缺少已有的設備使用信息，無法準確判斷設備的可靠性，多數情況下僅僅依靠設計師的經驗來保證。部分企業會采用故障模式、影響及危害性分 析（failure mode, effects and criticality analysis，FMECA）方法對已投產的設備的進行可靠性分析，但傳統FMECA方法在進行設計階段的可靠性分析時，對專家權重的分配不合理，不同情境下可靠性評估因素間的相對重要性也不一樣，因此得出的分析結果準備性較差[2-3]。程攀[4]根據專家的職稱以及工作年限等，賦予專家不同的權重，然后采用加權平均數的方法來進行危害性分析。劉澤銳[5]對傳統風險系數法進行改進，用故障發生概率與故障造成的停機時間的乘積來表示危害性大小。夏軍[6]與陳玉忠[7]等人為風險優先數法的3個因素之間賦予相對權重，確定權重的方法有專家評分法、層次分析法和熵值法等，其中使用層次分析法的較多。

本文以某家電企業研發的洗衣機滾筒自動裝配線為研究對象，對傳統的FMECA方法進行改進后，利用改進后的FMECA方法對洗衣機滾筒裝配線進行了可靠性分析，并將改進前后的分析結果進行對比，驗證了改進FMECA方法的準確性。

1 改進FMECA方法

首先對專家的賦權方式進行改進，采用依賴不確定性有序加權平均算法[8]（depended uncertain ordered weighted averaging, DUOWA）對不同專家給出的故障發生概率等級（O）、故障嚴酷度等級（S）以及故障檢測難度等級（D）進行賦權，計算其加權平均值。相較于以往在分析前賦予專家固定權重，改為根據不同專家給出的結果不同，賦予其動態權重，這樣更具合理性。對于不同的設備，S、O、D的相對重要程度是不一樣的，傳統FMECA方法是將3個因素給與相同的權重，本文使用層次分析法對專家賦權后的3個因素S、O、D再次賦予權重；最后將兩次賦權后的S、O、D值相乘得到風險影響指數Qi。改進后的FMECA方法既對專家賦權方式進行改進，又考慮了影響因素間的相對權重，使得分析結果更加準確。

1.1 依賴不確定性有序加權平均算法

設有n個專家組成的專家小組對某故障模式進行評估，第k個專家評估的風險優先數表示為集合

下面通過運用依賴不確定性有序加權平均算法來綜合專家們的評估。

（1）計算這n個S、O、D的算術平均值為Ra={Sa,Oa,Da}，其中

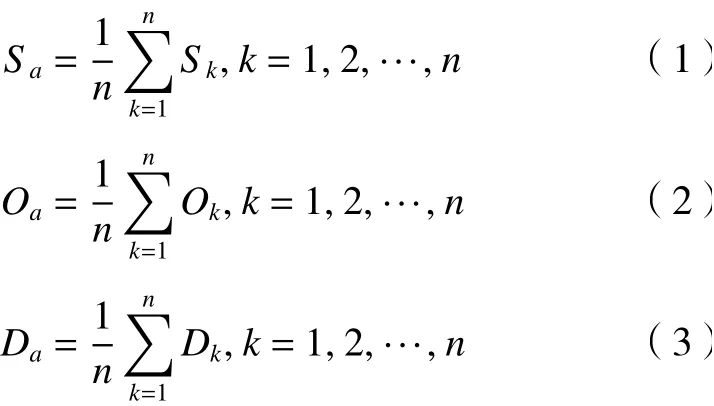
（2）計算Rk與Ra之間的測量距離為

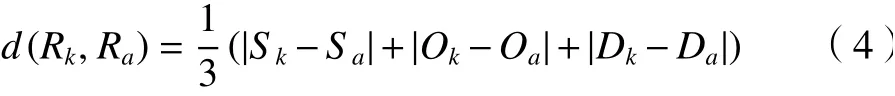
（3）計算Rk與Ra之間的相似度。對于n個風險優先數集合Rk={Sk,Ok,Dk}，下面給出其中每個風險優先數集合Rk與 這n個Ra的相似度的概念。

對于n個風險優先數集合Rk={Sk,Ok,Dk},k=1,2,···,n， 若Ra={Sa,Oa,Da}為它們的均值，則稱：

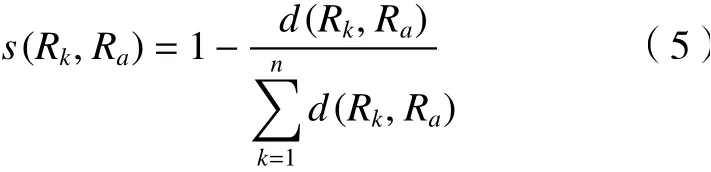
為風險優先數集合Rk={Sk,Ok,Dk}和其算術平均值Ra={Sa,Oa,Da}的相似度。

（4）集結。利用DUOWA算子的集結方式得到最終的集結公式

式（7）中：wk即為各專家的權重，R={S,O,D}為利用DUOWA算子加權后的風險優先數集合。

1.2 層次分析法確定各因素權重

（1）建立因素集。將影響評價指標的所有因素夠成一個集合R。

其中：ri表示評估對象的第i個因素。

（2）建立權重集。進行各故障模式危害性分析時，因各影響因素對危害性結果的影響程度不同，因而需對各影響因素進行加權優化，設影響因素權重集為

其中：ai是各影響因素對應的權重大小，即表明因素集R中元素ri在故障模式危害性分析時影響程度的相對權重值。本文采用層次分析法來確定風險優先數3個因素的相對權重值。對于兩個影響因素m與n，其層次分析法的標度表如表1所示。

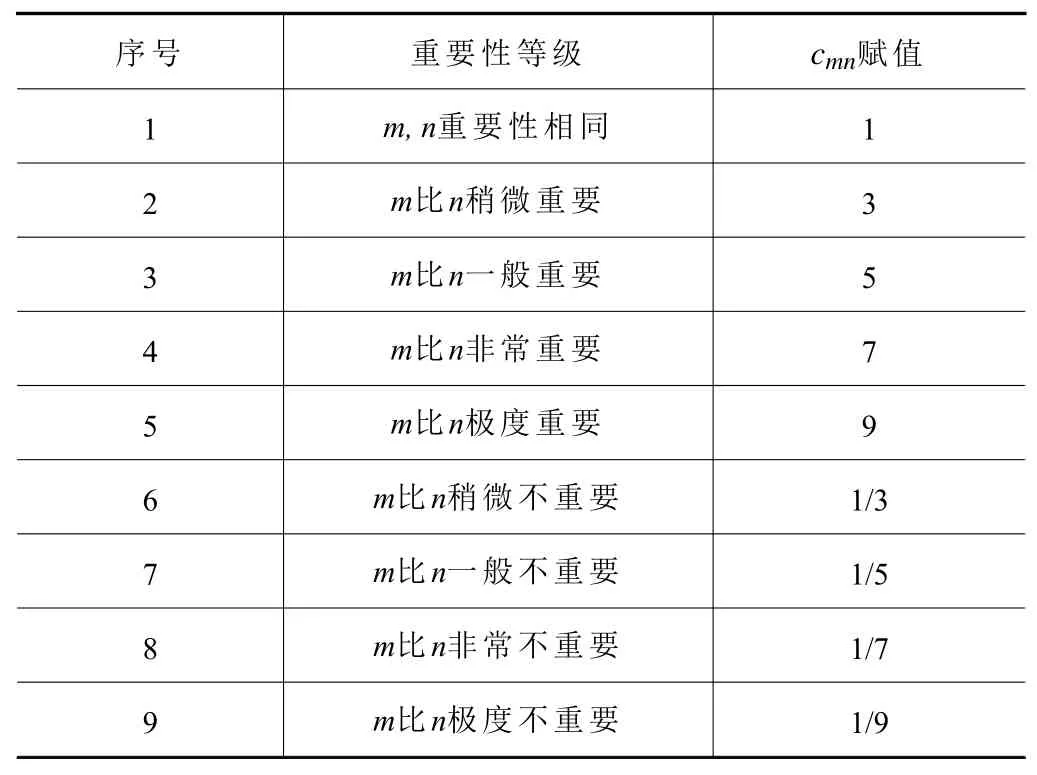
表1 層次分析法標度表

根據標度表對3個因素S、O、D進行評價，由實際情況和專家評價來確定兩兩之間的相對重要程度。然后根據標度表進行賦值，構成判定矩陣如下。

判定矩陣構造完成后，下一步計算矩陣的特征向量 ξ=[λ1,λ2,···,λn]，對特征向量歸一化處理，得到的向量即為各影響因素的權重集。

（3）一致性驗證。在得到權重集后，需要驗證結果的是否合理，采用的方法是進行矩陣的一致性驗證。首先求判定矩陣的一致一般性Ic，其計算公式如下

式中： λmax為判定矩陣的最大特征值；n為判定矩陣的階數。

得到判定矩陣的一致一般性Ic后，接著計算矩陣的平均隨機一致性Rc，計算公式為

其中：IR是由矩陣的階數所決定的，可通過查表獲得。當計算得到的矩陣平均隨機一致性Rc小于0.1時，說明判定矩陣C滿足一致性要求；反之，則需要改變判定矩陣C中各元素數值的大小，即重新判斷各因素兩兩之間的相對重要性，從而保確保得到的判定矩陣平均隨機一致性小于0.1。

1.3 風險影響指數Qi的計算

（1）計算專家賦權后的3個風險因素值S1、O1、D1

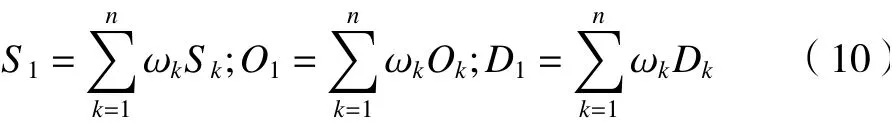
（2）根據層次分析法得到特征向量 ξ=[λ1,λ2,λ3]，歸一化處理后得到權重向量 μ=(μ1,μ2,μ3)，對專家賦權后的風險因素值S1、O1、D1加權計算得到S2、O2、D2。

（3）將考慮專家權重以及因素間相對權重的S2、O2、D2相乘即得到改進后的RPN值。由于經過兩次賦權后的3個因素值與原來相差較大，相乘后得到的RPN值也同樣如此。為了與改進前的風險優先數RPN區分開，將改進后的RPN值定義為風險影響指數Qi，計算公式如下。

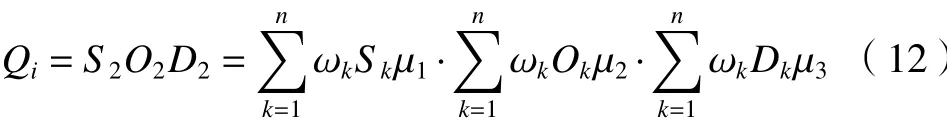
式中：wk即為各專家的權重；Sk、Ok、Dk為不同專家對同一故障模式給出的評價等級；μ1、μ2、μ3為S、O、D間的相對權重大小。

1.4 改進FMECA方法步驟

改進后的FEMCA分析步驟如圖1所示。

圖1 改進FMECA流程圖

2 基于改進FMECA裝配線可靠性分析

將洗衣機滾筒裝配線作為初始約定層次，約定層次為各站的組成模塊，如軸承與油封壓裝站的上料模塊。可靠性分析模型如圖2所示，圖中數字代表裝配線中各模塊的代號。

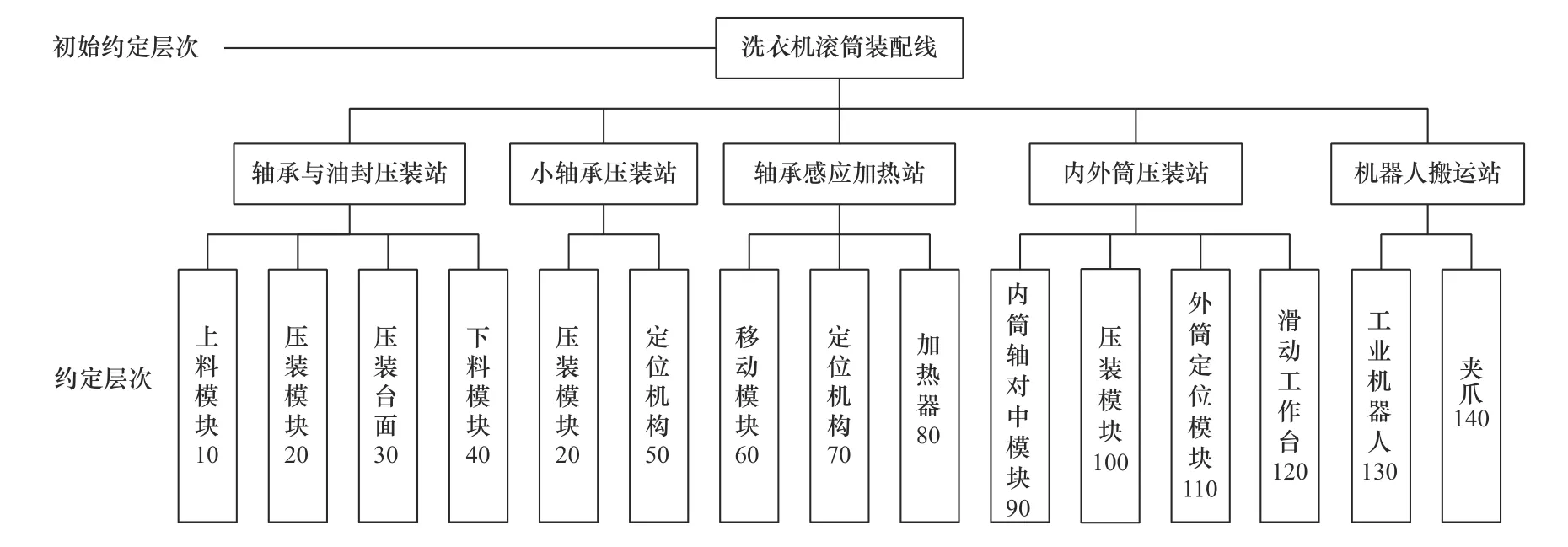
圖2 洗衣機滾筒自動裝配線分析模型

2.1 自動裝配線故障模式分析

對洗衣機滾筒自動裝配線進行FMEA分析，結果如表2所示。

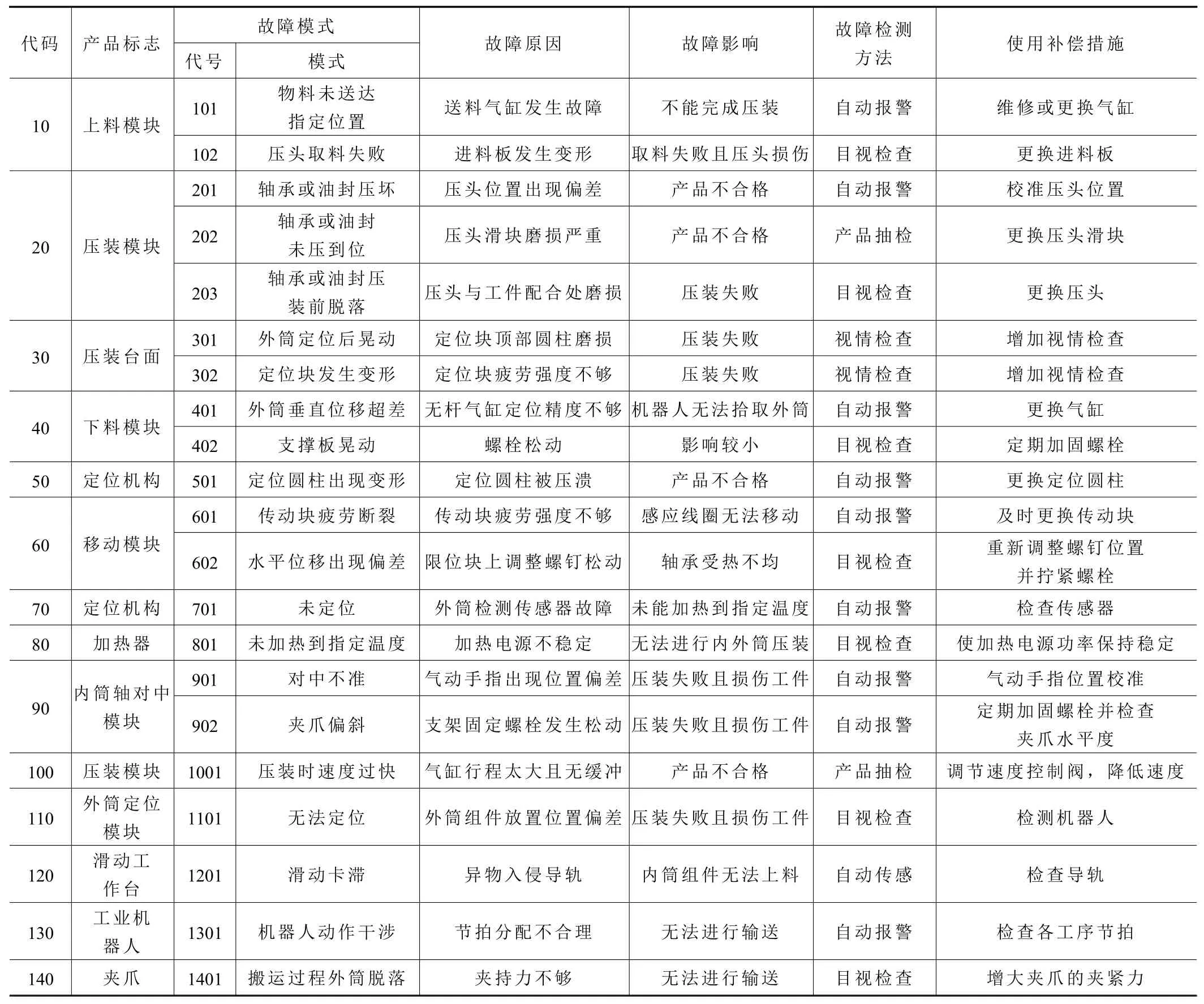
表2 故障模式及影響（FMEA）表

2.2 危害性分析

根據改進FMECA方法，成立一個危害性分析專家小組，該小組由4位熟悉非標自動化設計的專家組成，對每個故障模式進行評價。評價指標共3個：故障嚴酷度等級S、故障發生概率等級O、故障檢測難度等級D。由4位專家對每個故障模式進行評價，評價集合為Rk={Sk,Ok,Dk}。4位專家的評價集合見表3。

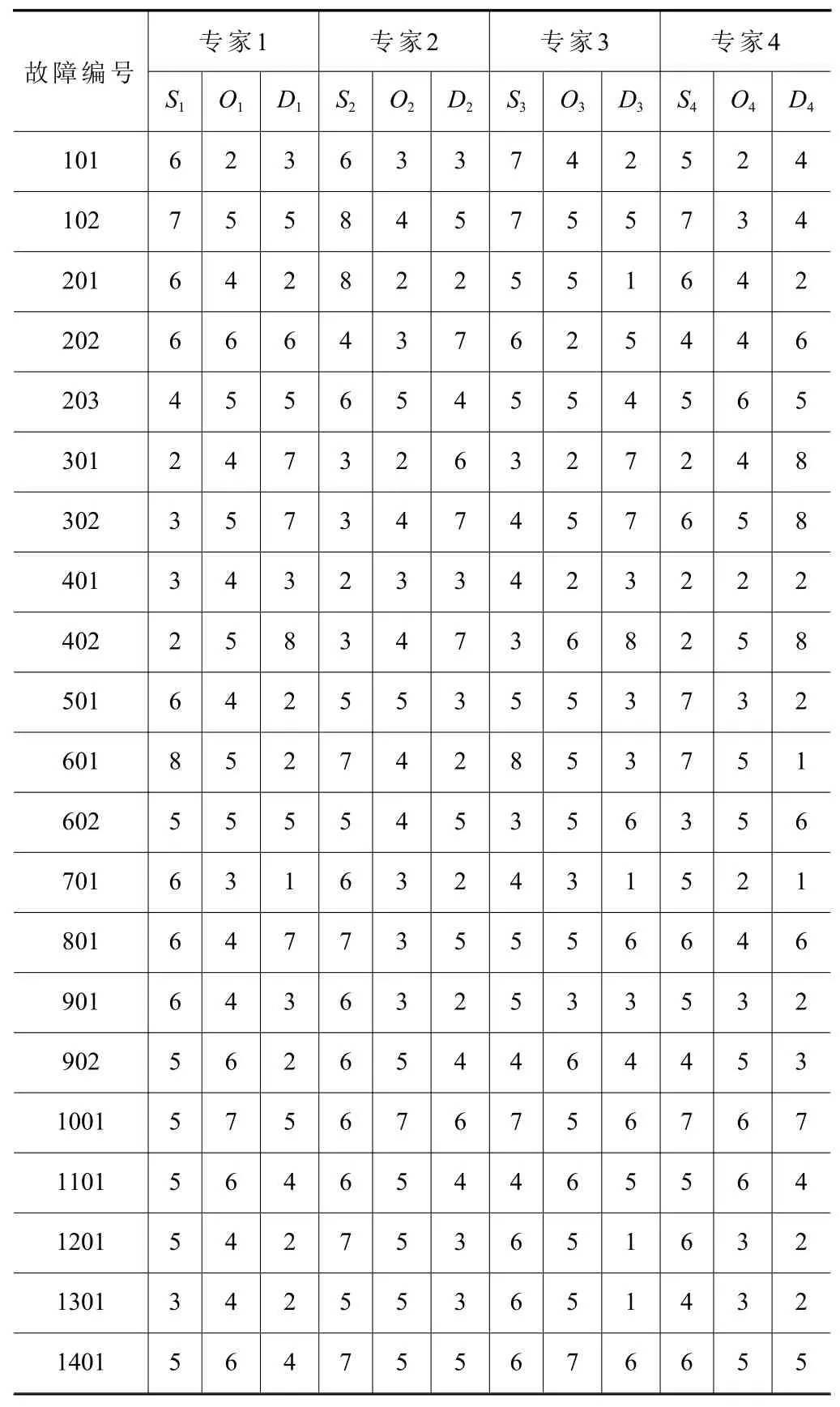
表3 故障模式危害性評分表

采用改進后的FMECA分析方法，計算各故障模式的風險優先數RPN與風險影響指數Qi，并分別進行排序，結果如表4所示。

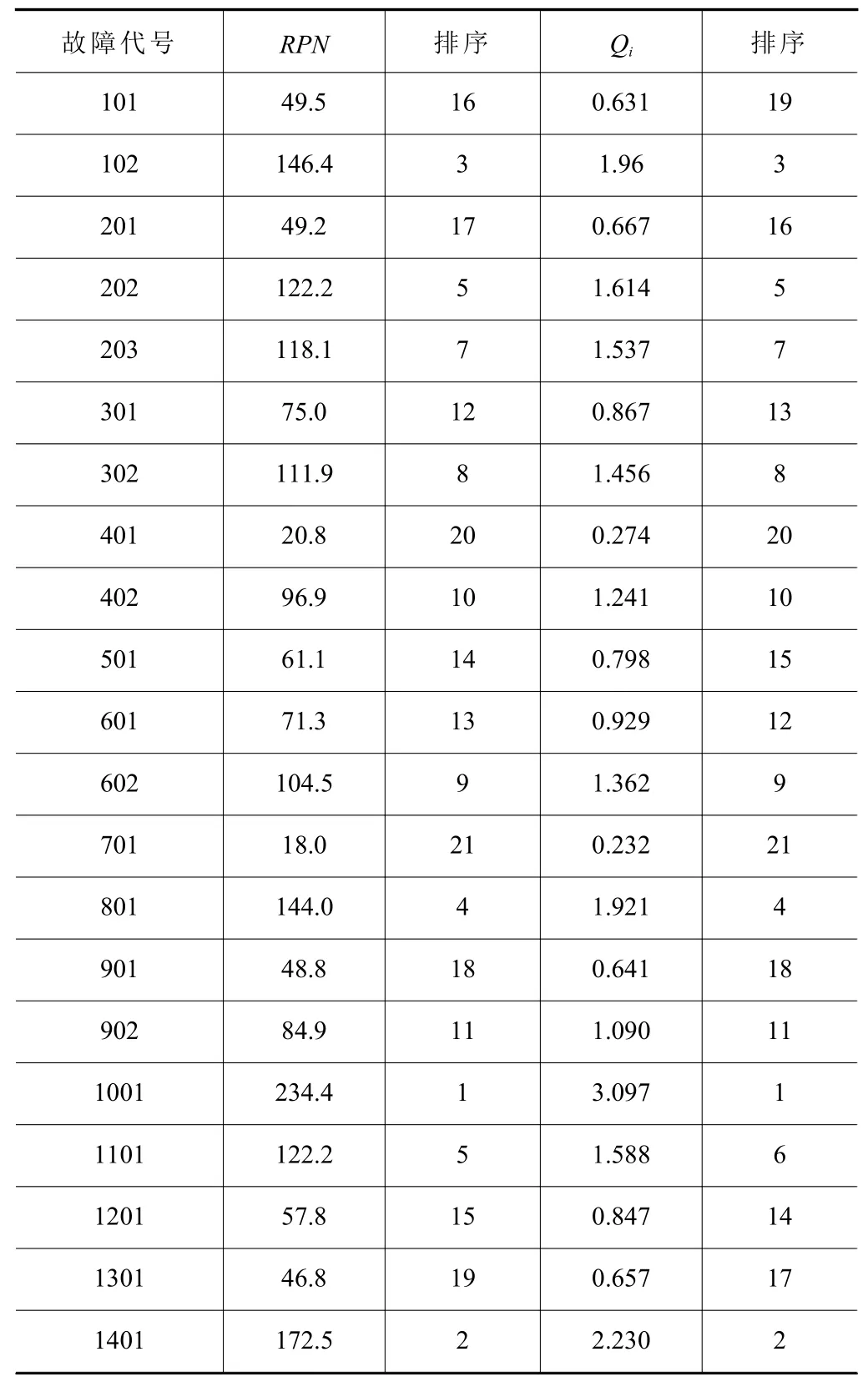
表4 故障模式危害排序

2.3 改進FMECA與傳統RPN排序結果對比

對比改進FMECA方法前后對洗衣機滾筒裝配線故障模式危害性排序，總體結果大致相同，只是某些故障模式的排序上存在細微差別，具體如圖3所示。但改進后的FMECA分析方法能夠削弱部分專家偶爾出現的判斷失誤，并且考慮到三因素的不同權重，使分析結果更符合實際情況。

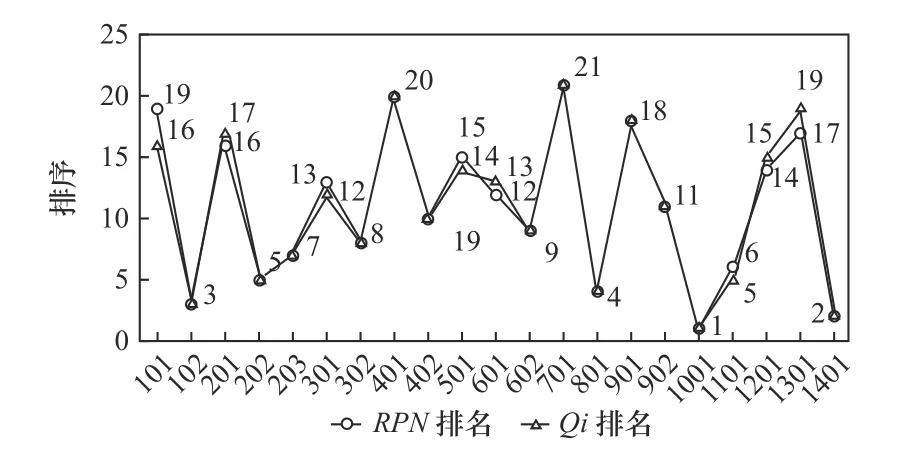
圖3 FMECA改進前后排序對比圖

3 結語

本文主要對傳統FMECA方法進行了改進，將依賴不確定性有序加權平均算法與層次分析法結合到一起，把風險優先數RPN改進為風險影響指數Qi，提高了非標自動化設備可靠性分析的準確性。并根據改進FMECA方法對洗衣機滾筒裝配線進行了可靠性分析，將改進前后分析結果進行對比，驗證了改進FMECA方法的合理性以及一定程度上提高了準確性。