無人機電力電纜安全巡檢關鍵技術開發與應用

田志平

（沈陽煤業（集團）機械制造有限公司， 遼寧 沈陽 110123）

引言

利用無人機對電力線路進行檢測的研究已經在人工智能領域展開。James 提出了一種遺傳算法（GA） 來獲得支持最短長度的有效巡檢路徑[1]。Prostejovsky 提出了一種基于四元數代數的無人機視覺檢測高度控制系統，為了解決電力線檢測的實時感知問題，提出了一種名為pline 的電力線檢測算法[2]。采用遺傳算法和粒子群優化相結合的方法，以最小化執行時間為目標，設計了一種復雜三維環境下的無人機軌跡調度方法。這些工作主要集中在如何利用無人機實現電力線檢測系統，而沒有考慮無人機的能量消耗和通信資源分配問題[3]。

無人機的能量效率問題在相關文獻中進行了研究。無人機作為地面節點的通信中繼，通過對其速度和負載進行聯合優化，使網絡能量效率最大化。多架無人機的部署在考慮能量約束的情況下，以飛行時間最小為目標進行優化。通過無人機軌跡優化，綜合考慮通信吞吐量和無人機能耗，研究了無人機與地面終端之間的節能通信問題。Strasser 提出了一種無人機作為空中基站服務于地面設備的節能資源分配方案。Maharjan 提出了一種名為“平均模型”的參考小無人機模型，同時解決了飛機的穩定性和功耗問題。Golshani 提出了一種太陽能無人機的能量優化方法，即通過控制飛行姿態來優化飛行軌跡。

1 原理和方法

1.1 系統模型

1.1.1 電力線檢測模型

基于無人機的電力線檢測模型如圖1 所示。電網拓撲可以看作是一個圖。

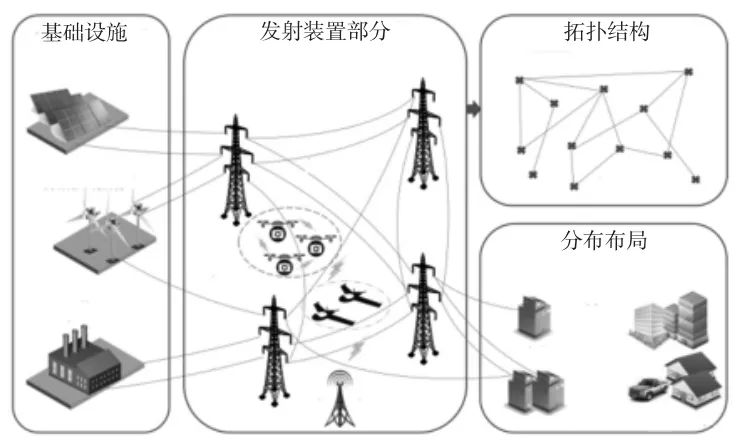
圖1 基于無人機的電力線檢測模型示意圖

在檢測過程中，無人機在電力線周圍形成一個簇，并以相同的速度向前飛行，以便在同一時間內提供同一位置的多角度檢測。安裝在每個IUAV 上的通信設備有兩個功能，分別是避免碰撞和圖像數據傳輸。一方面，每個IUAV 每秒廣播若干預定義信標，用于接收信號強度（RSS）為基礎的距離測量。采用store-carry-forward-based 數據傳輸方法，所收集的IUAVs 數據暫時存儲在本地存儲設備，然后將數據傳輸到電網公司的服務器，對其進行處理和分析，找出潛在的問題，因此，數據傳輸是容忍延遲的。至于優化數據傳遞延遲，會在以后的工作中考慮。值得注意的是，正在執行其他任務的無人機，碰巧出現在無人潛航器附近，并不總是可用的。

1.1.2 推進能耗模型

采用穩態直線水平飛行（SSLF）模型建立推進能量消耗模型。SSLF 模型包含以下兩個方面：一為IUAV 以恒定的速度向固定方向飛行，沒有水平加速度和突然轉彎；二為由于升重平衡，IUAV 在沒有垂直加速度的情況下以恒定高度飛行。

1.1.3 碰撞能耗模型

避碰方案由三個階段組成，分別是距離估計、碰撞警告和控制行動。只考慮距離估計的能量消耗，因為避碰控制規則和動作不在本工作的范圍內。在無人機飛行過程中的標定距離為（k，k0），用來估計IUAV 間的距離，IUAV 需采用連續廣播信標，廣播信標的頻率為（fk，k0）。考慮到噪聲引起的估計不完全，定義了（δk，k0）作為距離的最大估計誤差，可以通過碰撞預警和控制動作來補償，從而實現成功的避碰。最大估計誤差大于（δk，k0）的概率定義為Pr（δk，k0）。

1.2 兩級節能電力線路檢測算法

結合動態規劃、拍賣理論和匹配理論提出節能電力線檢測算法。首先，將聯合優化問題轉化為基于能耗大小和優化時間差異的兩階段優化問題；在此基礎上，提出了一種基于動態規劃的大規模優化方案，第二階段結合拍賣理論和匹配理論求解小時間尺度優化問題。

1.2.1 聯合優化問題轉化

制定聯合優化問題，其中包括兩個軌跡等優化調度、速度控制和頻率調節、固定的值在一段和不同時間尺度的秒，和繼電器等優化選擇和功率分配的值取決于信道衰落和毫秒時間尺度的變化。此外，大時間尺度優化問題的能耗目標值一般比小時間尺度優化問題的能耗目標值高幾個數量級。

因此，為了提供解決方案，利用大時間尺度優化和小時間尺度優化之間的時間尺度差異作為先驗知識來簡化問題。大型時間表問題的解決在第一階段不考慮第二階段優化問題，然后時域問題已經解決了在第二階段基于第一階段的最優結果。因此，所提出的兩階段算法由于沒有同時進行軌跡調度、速度控制、頻率調節和功率分配的聯合優化，會導致性能次優。

1.2.2 基于動態規劃的節能軌跡調度、速度控制和頻率調節

在本工作中，接下來采用DP 算法求解聯合優化問題，該算法基于得到的每個分段的最小能量消耗。其原因在于DP 是一種經典的求最優解的算法，可以作為評價其他啟發式算法的較高性能基準。

在DP 系統狀態的演化的影響下，在離散階段決策是由xτ+1=z（xτ，uτ）來決定的，其中τ=0，1，2，···，ψ-1，其中ψ 是階段的總數，τ 是階段系數，xτ和xτ+1是階段τ 和階段τ+1 的決策，假設uτ是τ 決定階段z 為列舉狀態下的更新機制，將狀態集設為目標點集，如xτ=k，將決策集設為軌跡調度變量集，如則狀態更新形式為：

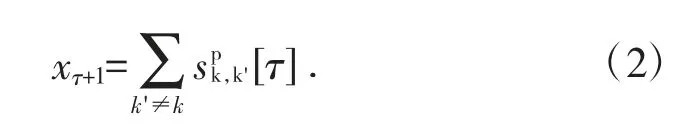
需要從目標點k 移動到目標點k'，IUAV 在初始階段x 時的最小能量消耗為0。

2 試驗驗證

在本節中，基于真實電網拓撲對所提出的兩階段能耗最小化算法進行評估。

圖2 顯示了路段能耗、飛行速度和距離估計信標的廣播頻率。能量消耗隨速度增加先減小后增大，隨廣播頻率單調增加。這是因為當單位速度增量所增加的推進能量消耗小于減少飛行持續時間所節省的能量時，能量消耗會隨著速度的增加而減少。反之，能量消耗隨速度增加而增加。

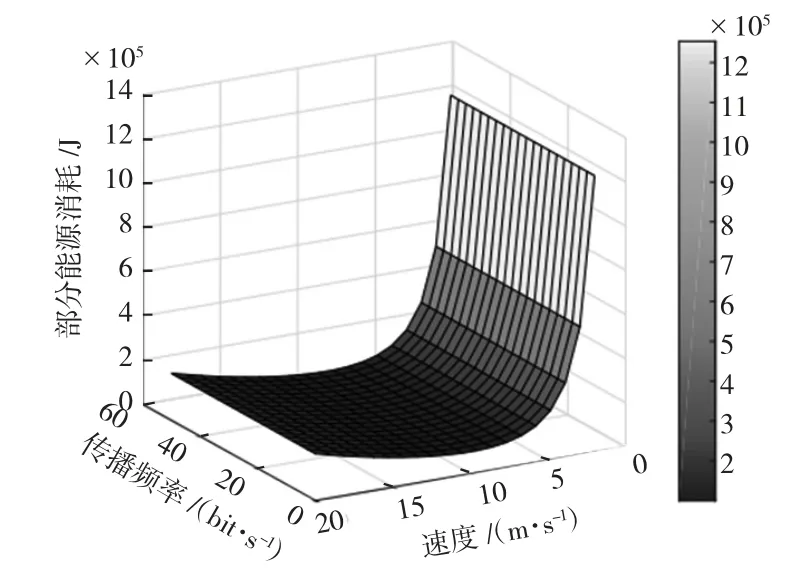
圖2 能量消耗與飛行速度、信標廣播頻率的關系

圖3為目標點數對總能耗的影響。貪婪算法總是選擇點能量消耗最小的分段每個階段，以及隨機決定軌道、速度、廣播頻率、中繼、發射功率的隨機方案進行比較。數值結果表明，三種算法的能耗性能均隨著目標點數的增加而增加。然而，所提算法的能量消耗增長率即曲線斜率，從能源效率角度考慮，由于多變量聯合優化，曲線斜率遠低于兩種啟發式算法。

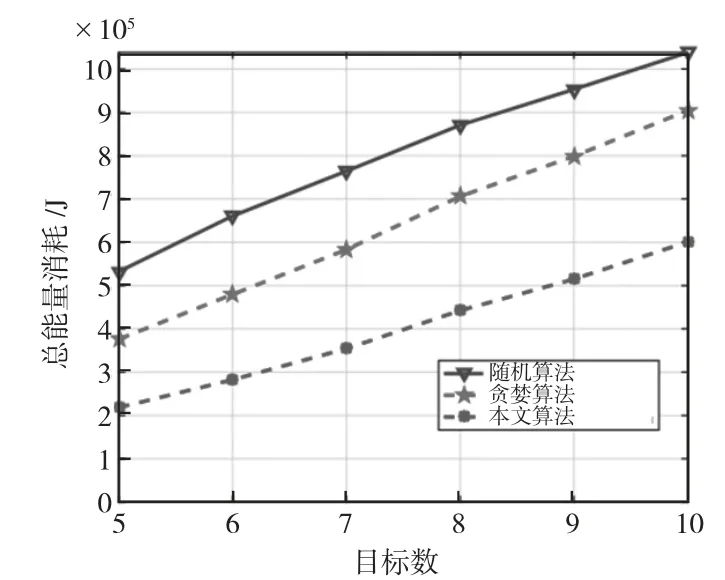
圖3 目標點數對總能耗的影響

下頁圖4 顯示了第二級能量消耗與無人機數量的關系。采用通過檢查每個可能的組合來獲得最優性能的蠻力搜索方案作為性能基準。結果表明，當無人機數量N=5 時，該算法可達到最優性能的87.6%，比隨機分配方案的性能提高了41.8%以上。背后的原因是繼電器的選擇啟發式算法不與功率控制聯合優化。

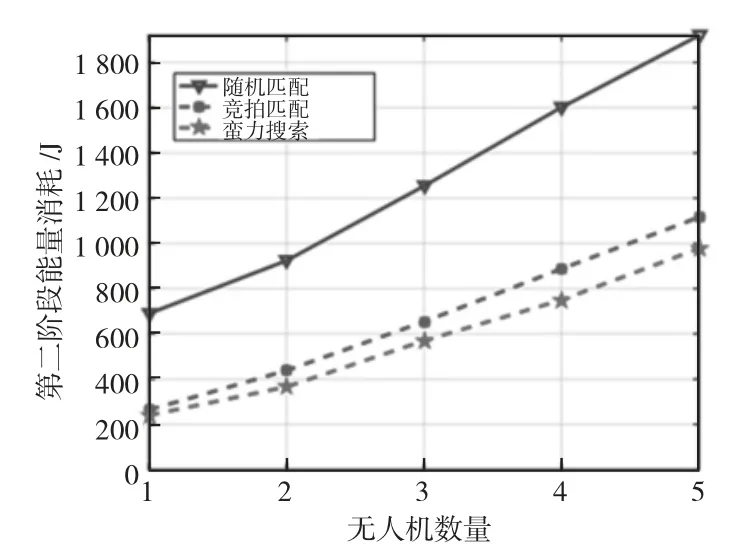
圖4 第二階段的能耗與無人機數量的對比

下頁圖5 顯示了降低能耗和計算復雜度之間的權衡。數值結果表明，聯合優化軌跡調度、速度控制和頻率調節可在增加73.2%計算復雜度的前提下，實現75.1%的節能增益。特別需要指出的是，與總能耗相比，繼電器選擇和功率分配的聯合優化所節省的能量是微不足道的。其原因是推進功率通常比數據傳輸功率高幾個數量級。因此，需要適當考慮節能收益和計算復雜性成本，以實現滿意的能效性能。

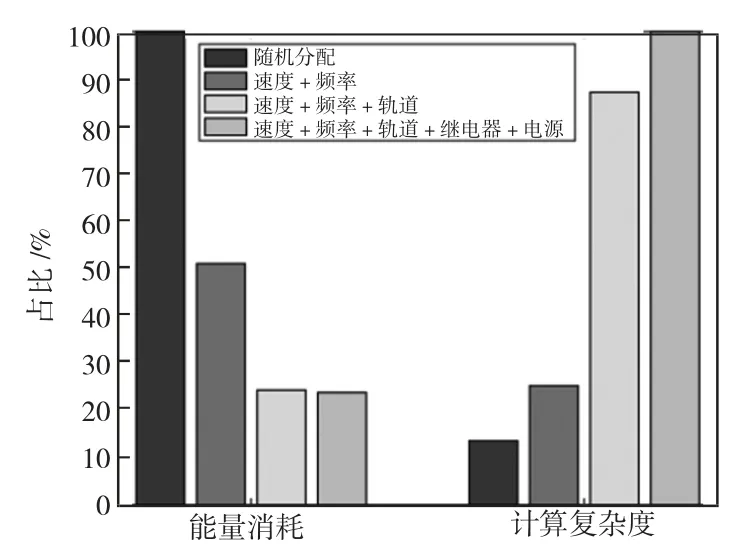
圖5 降低能耗和計算復雜度之間的權衡

3 結論

本文以基于無人機智能電網電力線檢測為研究對象，提出了一種兩級節能型聯合軌跡調度、速度控制、頻率調節和功率分配算法。將該算法與其他基于真實地圖和電網拓撲的啟發式算法進行了比較，并通過數值結果驗證了該算法在節能方面的優越性。