基于證據理論層次分析法的云貝葉斯網絡在預警雷達毀傷效果評估中的應用

鄧力源， 楊萍， 劉衛東， 汪江鵬

(火箭軍工程大學 基礎部 數學室, 陜西 西安 710025)

0 引言

目標毀傷效果評估作為作戰能力分析與火力規劃研究的基礎，一直是作戰問題研究的熱點之一。目標毀傷效果評估方法主要有貝葉斯網絡法、毀傷樹法、故障樹法、作戰環法、神經網絡法、模糊綜合評判法等，這些方法在目標毀傷效果評估中得到了較為廣泛的運用，但在處理具有一定關聯性的定性、定量指標等不確定性與模糊性較強的問題時，評估效果準確性欠佳。

云模型是一種能夠實現定性概念與定量概念之間相互轉化的數學模型，在處理不確定性與模糊性問題上有獨特的優勢，已運用于質量管理、應急決策、風險評估等領域。云模型在軍事領域的應用也十分廣泛，李琳琳等構建了作戰指揮控制系統的效能評估指標體系，引入綜合云模型對體系效能進行了評估。范陽濤等針對軍隊信息化條件下軍事訓練的新特點，提出了基于云模型的軍隊信息化條件下軍事訓練評估方法。劉崇屹等提出一種基于改進層次分析(AHP)法與云模型的質量評估方法，彌補了傳統導彈雷達導引頭質量評估方法的不足。董華清等提出一種結合云理論與模糊模型的綜合評估方法，對遠程預警系統的性能進行了合理評估。王雙川等針對灰色云模型在解決實際問題中的局限性，建立了非對稱灰色云模型，并對裝備維修保障系統的效能進行了評估。

云模型也廣泛運用于目標毀傷效果評估中。張成等根據云重心評判法原理，提出一種基于云重心評判法的目標毀傷效果評估方法，并應用于對空軍基地毀傷效果的評估。杜詩瑞等在裝甲目標的毀傷評估中引入云模型，將裝甲目標的物理毀傷度值轉化為功能毀傷度值與總體毀傷度值。

同時，將云模型理論與貝葉斯網絡推理思想相結合，在求得目標各毀傷等級概率的同時，亦可求得具體毀傷值。曲婉嘉等結合云模型強大的知識表達能力與貝葉斯網絡在推理方面的優勢，構建了基于雷達目標的貝葉斯網絡毀傷模型，使用蒙特卡洛法進行參數學習得到條件概率表，通過推理求得目標各毀傷等級的概率，并利用云模型將概率值轉化為具體毀傷值。李陽等構建了基于圖像目標的貝葉斯網絡毀傷模型，結合試驗數據，使用最大似然估計法進行參數學習得到條件概率表，通過推理求得目標各毀傷等級概率，并利用云模型將概率值轉化為具體毀傷值。

文獻[19]在構建條件概率表時使用的蒙特卡洛法雖然能夠在一定程度上彌補數據樣本缺失的不利影響，但依靠隨機試驗得到的結果依然可能偏離實際。文獻[20]在構建條件概率表時使用的最大似然估計法對實驗數據的要求較高，若實驗數據出現缺漏或記錄錯誤，則所得結果可信度必然受到影響。

除了文獻[19]中使用的蒙特卡洛法與文獻[20]中使用的最大似然估計法，實際問題中，在給定貝葉斯網絡拓撲結構的前提下，還可依據專家經驗，通過引用直覺模糊函數、相對比較推斷等方法得到條件概率。但傳統的依據專家經驗推導條件概率的方法因各專家在研究領域、知識結構、認知水平、思維模式等層面的區別，所得結果往往是不完整或者片面的。

對預警雷達的毀傷方式主要有硬毀傷模式與軟毀傷模式兩種類型。其中，硬毀傷模式即利用各型空、地武器平臺發射導彈對預警雷達目標實施精確打擊；軟毀傷模式即可利用先進的電子干擾平臺對預警雷達實施針對性干擾，以使得預警雷達部分或完全喪失作戰能力。本文主要以針對預警雷達的軟毀傷模式為研究對象，在傳統貝葉斯網絡模型的基礎上引入云模型，建立預警雷達遭受電子干擾平臺干擾的軟毀傷效果評估模型。

針對傳統依靠專家經驗推導條件概率方法的局限性，本文采用結合證據理論(DS)與AHP法的DS/AHP方法確定各節點條件概率值，解決傳統方法在確定條件概率過程中存在的問題。同時結合云模型理論與貝葉斯網絡推理思想，在求得預警雷達各毀傷等級概率的同時，亦可求得各毀傷等級對應的具體毀傷值。最后，通過數學分析軟件MATLAB中的聯合樹法實現預警雷達毀傷效果的評估。

1 基于DS/AHP云貝葉斯網絡的目標毀傷效果評估流程

貝葉斯網絡和云理論在推理能力與知識表達能力方面各有所長。云貝葉斯網絡是一種結合了貝葉斯網絡的推理能力與云模型的知識表達能力，兼具隨機性與模糊性的推理模型，其推理流程如圖1所示。

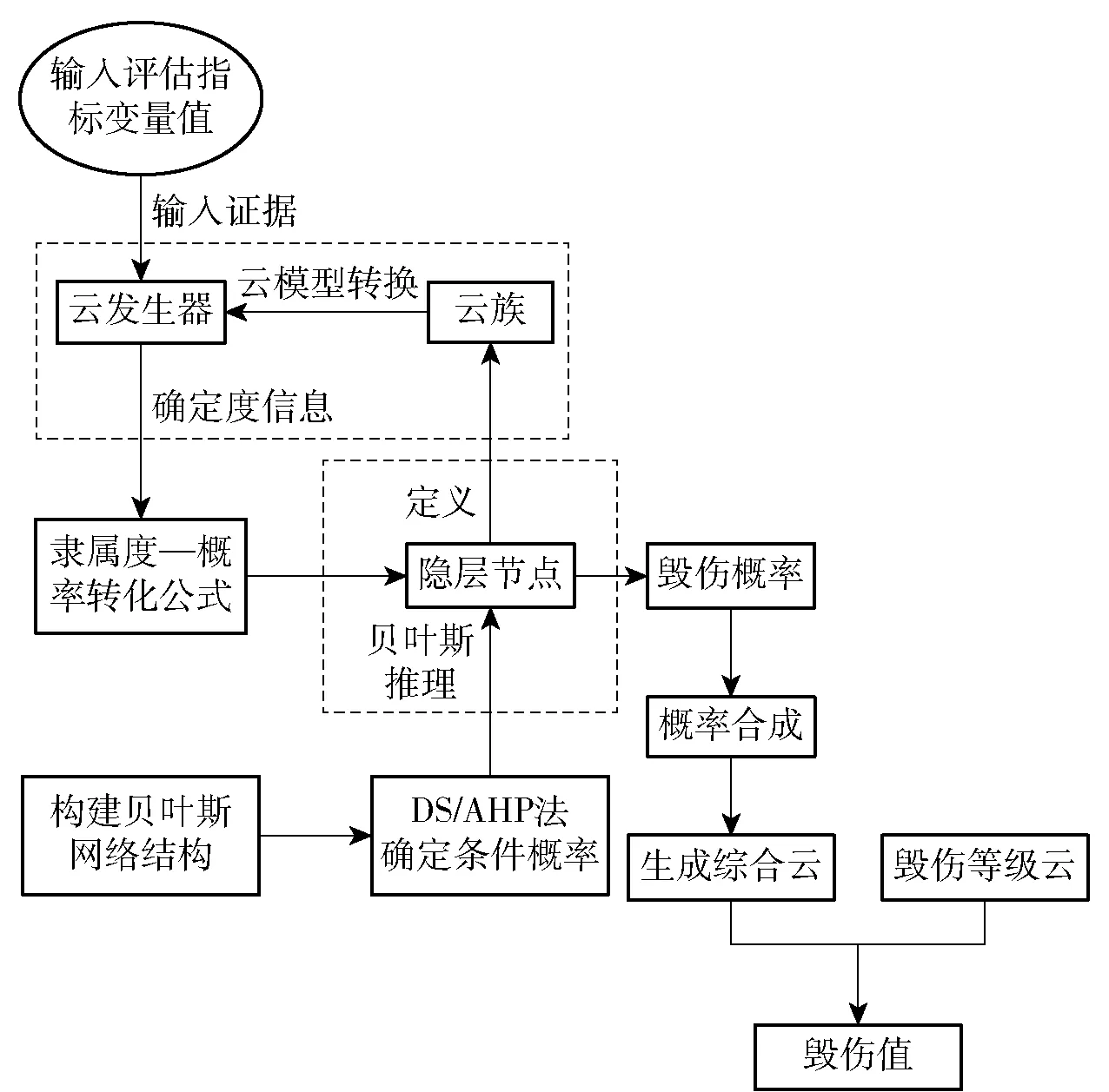
圖1 云貝葉斯網絡推理流程Fig.1 Reasoning process of cloudy Bayesian network

云貝葉斯網絡的推理步驟如下：

1)根據作戰問題背景確定貝葉斯網絡結構；

2)確定評估指標體系，對指標體系內的變量進行歸一化處理，定義節點云族并設計云發生器；

3)對變量進行云模型轉換，得到變量對應的隸屬度，比較變量對論域內不同等級狀態的隸屬度，依據最大判定準則，確定最大隸屬度對應的隸屬云即為指標對應等級狀態；

4)生成目標的毀傷等級云；

5)依據DS/AHP方法確定各節點條件概率分布；

6)通過隸屬度—概率轉換公式將隸屬度轉換為概率，將節點概率代入貝葉斯網絡進行推理，得到節點毀傷概率；

7)重復步驟4～步驟5，綜合考慮計算時間與計算量的影響，重復計算次數不少于50次，記錄各次運算結果，利用概率合成公式得到各毀傷等級概率。

2 毀傷效果評估模型的構建

2.1 構建貝葉斯網絡模型

影響預警雷達毀傷程度的因素主要有干擾平臺屬性(干擾角度、干擾距離)、干擾時間、干擾功率、干擾頻率、干擾樣式、抗干擾措施、工作體制與響應機制。以上因素可歸納為干擾機攻擊能力與雷達抗毀傷能力兩個主要方面，其中：干擾平臺屬性(干擾角度、干擾距離)、干擾時間、干擾功率、干擾頻率、干擾樣式屬于干擾機攻擊能力；抗干擾措施、工作體制、響應機制屬于雷達抗毀傷能力。可建立圖2所示預警雷達毀傷貝葉斯網絡模型。

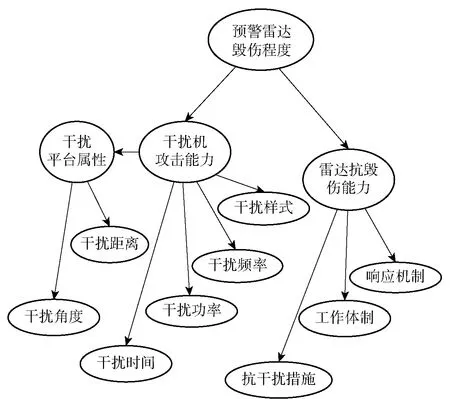
圖2 預警雷達毀傷貝葉斯網絡模型Fig.2 Bayesian network model of early warning radar damage

2.2 確定評估指標體系

根據圖2模型，可確定評估指標體系。定義干擾機攻擊能力與雷達抗毀傷能力為{很強,強,中,弱}4個狀態。

2.2.1 干擾機攻擊能力評估指標體系

2.2.1.1 干擾平臺屬性

影響干擾平臺屬性的因素有干擾機的角度、干擾機與預警雷達的距離。定義干擾平臺屬性為{很強,強,中,弱}4個狀態。

設干擾機與雷達主瓣的方向角為，定義預警雷達天線接收增益- 角度系數：

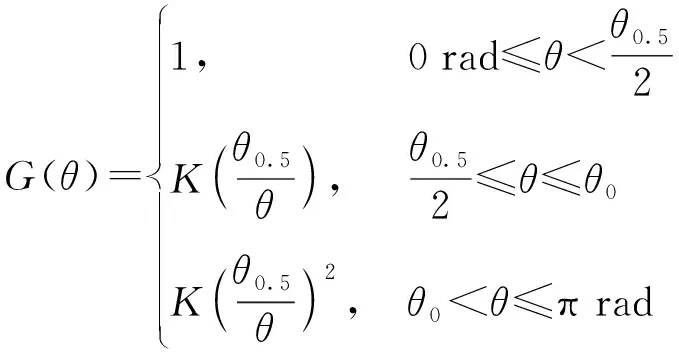
(1)

式中：為預警雷達與干擾機之間的夾角；05為預警雷達天線波瓣寬度；為增益系數，∈[002, 010]。越小，預警雷達天線接收增益就越大，干擾效果越好。定義干擾角度為{大,中,小}3個狀態。

干擾機對預警雷達實施有效干擾的必要條件是二者間的距離必須大于其最小壓制距離，最小壓制距離越小，雷達被壓制的區域越大，定義距離系數為

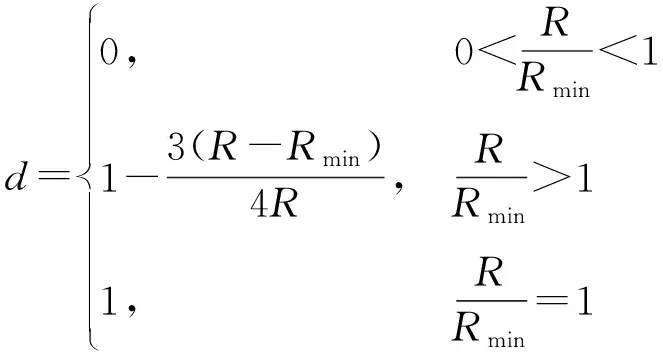
(2)

式中：為干擾平臺與預警雷達之間的距離。越大，干擾效果越好。定義干擾距離為{遠,中,近}3個狀態。

2212 干擾時間

對預警雷達實施干擾要在一定有效的時間段內進行。設Δ表示預警雷達開機后工作時間段，Δ表示干擾機在預警雷達開機后工作時間段內實施有效干擾的時間段。定義雷達干擾時域瞄準系數為

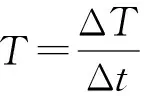
(3)

越大，干擾機在預警雷達開機后工作時間段內實施有效干擾的時間越長，干擾成功的概率越大。定義干擾時間為{長,中,短}3個狀態。

2213 干擾頻率

設干擾機干擾頻率區間為～，預警雷達工作頻率區間為～，干擾頻率區間越接近雷達工作頻率區間，干擾效果越好，定義雷達干擾頻率覆蓋系數為

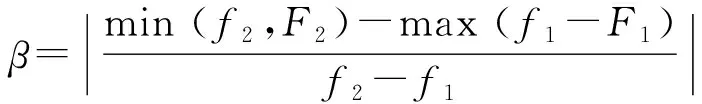
(4)

越大，干擾頻率區間對預警雷達工作頻率區間的覆蓋能力越強，偏離預警雷達工作頻率區間的程度越小，干擾效果越好。定義干擾頻率為{大,中,小}3個狀態。

2214 干擾功率

干擾功率越大，對預警雷達實施有效干擾的可能性越大。定義壓制系數為

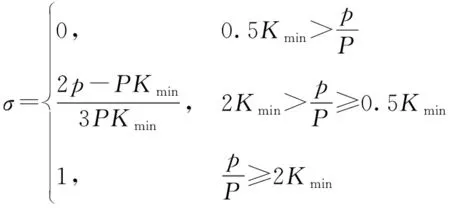
(5)

式中：為網軍對預警雷達實施有效干擾時預警雷達接收機輸入端需要輸入的最小干擾功率；為雷達回波功率；為保證雷達正常工作所需要的最小干信比。越大，干擾效果越好。定義干擾功率為{大,中,小}3個狀態。

2215 干擾樣式

干擾機干擾樣式越多，其與預警雷達工作體制匹配成功率越高，實施有效干擾可能性越大。設共有瞄準式干擾、阻塞式干擾、掃頻式干擾與欺騙式干擾等種干擾樣式，干擾機干擾樣式有(≤)種，定義干擾機干擾樣式系數為

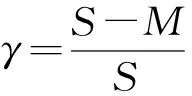
(6)

越小，干擾機對預警雷達實施有效干擾的可能性越大。定義干擾樣式為{多,中,少}3個狀態。

222 雷達抗毀傷能力評估指標體系

2221 工作體制

預警雷達常用工作體制如表1所示。

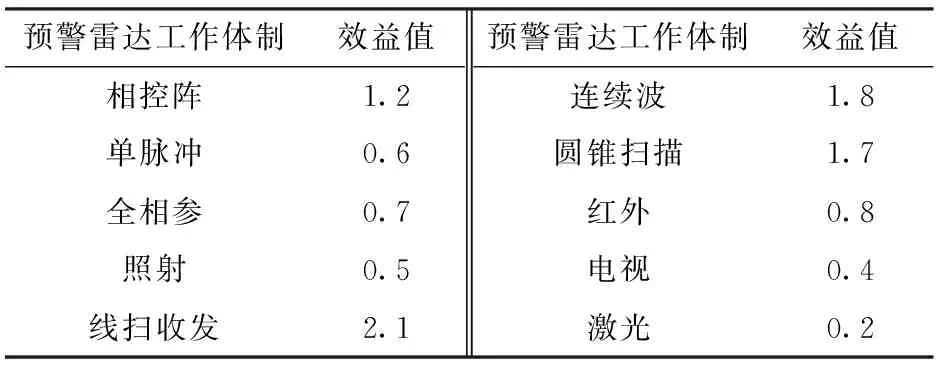
表1 預警雷達常用工作體制及效益值

定義預警雷達工作體制合成系數為

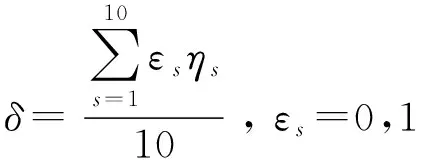
(7)

式中：為預警雷達采用第種工作體制對應的效益值，若預警雷達采用了第種工作體制，則=1，若預警雷達未采用第種工作體制，則=0。越大，預警雷達工作體制越先進，抗干擾能力越強。定義工作體制為{先進,普通,落后}3個狀態。

2222 抗干擾措施

預警雷達采用的抗干擾技術措施越多，干擾機對其實施有效干擾的可能性越小。其常用的抗干擾技術措施如表2所示。

定義預警雷達工作體制合成系數?為

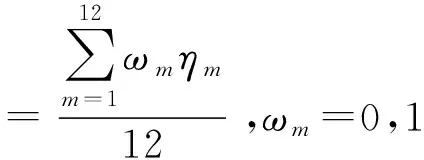
(8)

式中：為預警雷達采用第種抗干擾技術的效

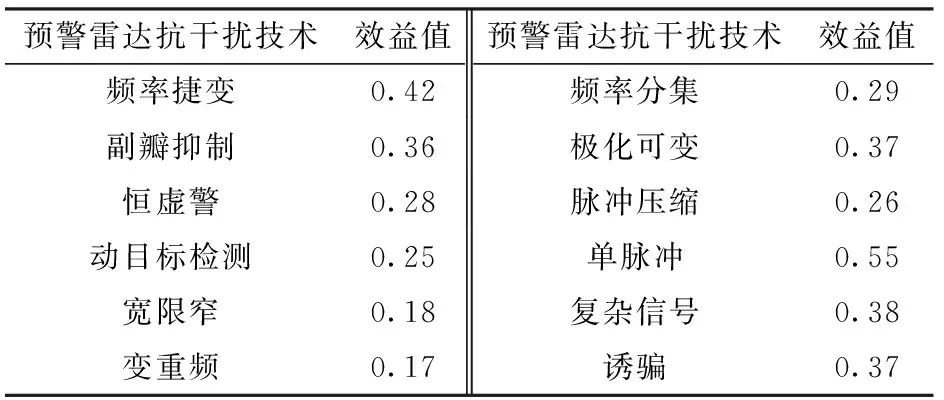
表2 預警雷達常用抗干擾技術及效益值

益值，若預警雷達采用了第種抗干擾技術，則=1，若預警雷達未采用第種抗干擾技術，則=0；為預警雷達采用的第種抗干擾措施對應的效益值。越大，預警雷達抗干擾能力越強。定義抗干擾措施為{多,中,少}3個狀態。

2223 備份(接替)能力

預警雷達在自身受到打擊而喪失作戰能力后，通常會啟動備份(接替)等響應機制，以彌補原雷達毀傷而引發的整體作戰能力的下降。設預警雷達啟動備份(接替)等響應機制的成功率為，定義響應概率密度函數()服從指數分布：

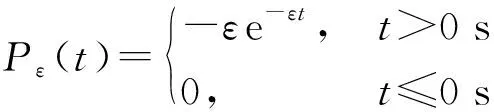
(9)

則預警雷達遭受攻擊后發生故障而處于停機狀態，經過時間啟動備份(接替)響應機制的成功率為

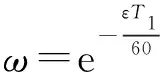
(10)

由(10)式可知，響應機制啟動時間越短，響應機制啟動成功率越大，預警雷達備份(接替)能力越強。定義響應機制為{快,中,慢}3個狀態。

2.3 體系變量歸一化處理

由于21節得到的指標體系變量的量綱與范圍均不相同，為了便于評估，采用如下原則對變量進行歸一化處理：

對于越大越好型指標，有

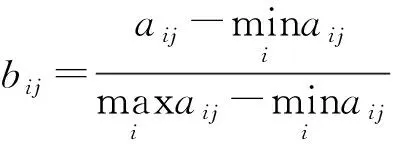
(11)

式中：為指標變量。

對于越小越好型指標，有

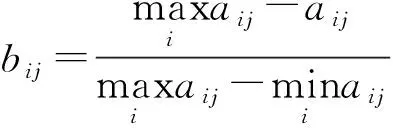
(12)

2.4 云模型轉換

云模型轉換即在歸一化處理后的指標體系變量的論域中定義一個云族，根據云族設計相應的云發生器，將指標體系變量輸入云發生器即可得到變量對應各定性概念的隸屬度。

由于正態云具有很強的普適性，本文選擇正態云定義云族。根據22節對各節點狀態的定義，對于有3個狀態的節點，在論域=[0,1]內設計云族，=(期望，熵，超熵)，分別表示為云族1(1)、云族2(2)、云族3(3)。其中，云族1=(015,005,0005)、云族2=(05,005,0005)、云族3=(05,005,0005)，如圖3所示。

圖3 有3個狀態的云族Fig.3 Cloud family with 3 states

對于有4個狀態的節點，在論域=[0,1]內設計4個云族，分別為1=(015,004,0004)、2=(035,004,0004)、3=(065,004,0004)、4=(09,004,0004)，如圖4所示。

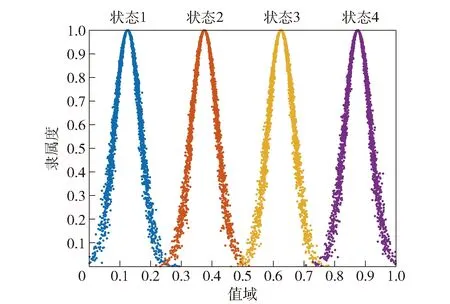
圖4 有4個狀態的云族Fig.4 Cloud family with 4 states

云發生器可實現定性概念與定量數據間的相互轉化。正向云發生器通過輸入云模型數字特征產生云滴，實現定性概念向定量數據轉化，如圖5所示。圖5中，為期望，為熵，為超熵，(,)為云滴，為特定值，為的確定度。

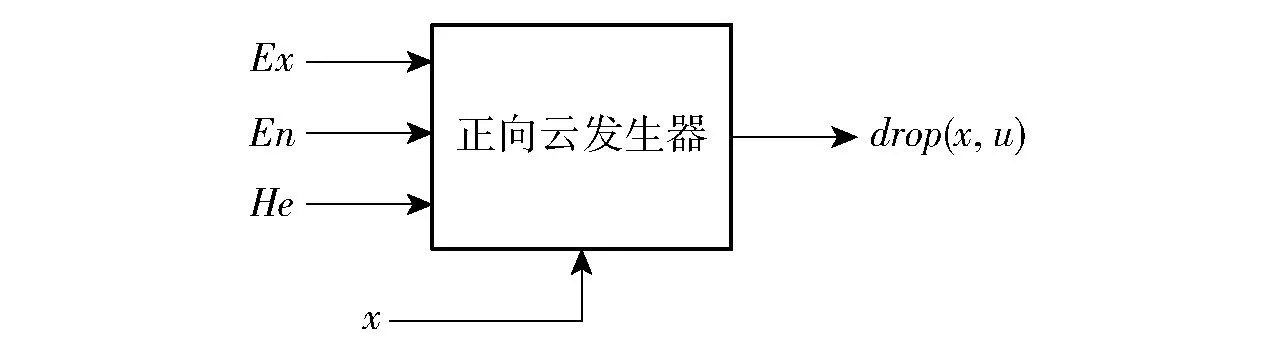
圖5 正向云發生器Fig.5 Forward cloud generator

正向云發生器的算法為：

輸入：定性概念的數字特征(,,)，特定值；

輸出：特定值對應的云滴(,)。

算法步驟為：

1) 生成一個正態隨機數：1=(，)。

2)計算特定值的確定度：

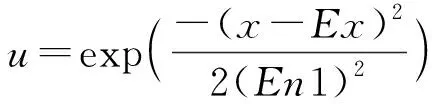
(13)

可利用隸屬度- 概率轉換公式將節點隸屬度轉換為可用于貝葉斯網絡推理的概率。概率- 隸屬度轉換公式為

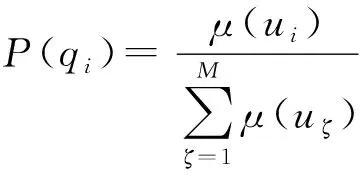
(14)

式中：為變量對論域的隸屬度；為隸屬度對應的值。

為消除云發生器產生云滴的不確定性影響，可經過多次推理并依據概率合成公式得到體系目標最終毀傷等級，具體步驟為：

1) 設體系目標有、、、…、共個毀傷等級，經過次推理后得到推理結果：

=[(),(),(),…,()]

(15)

2)分別合成各次推理結果，得到目標屬于各毀傷等級的概率為

=[(),(),(),…,()]

(16)

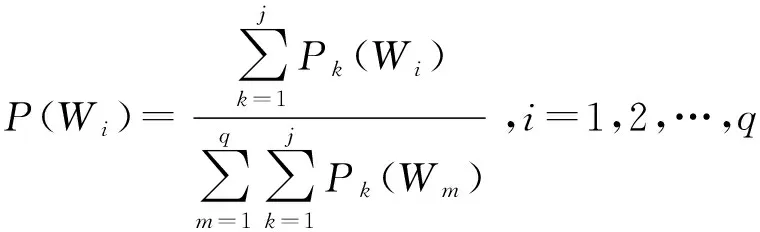
(17)

2.5 生成毀傷等級云

預警雷達毀傷程度可劃分為無毀傷、輕度毀傷、中度毀傷、重度毀傷、失能5個等級，對應毀傷值如表3所示。

表3 預警雷達毀傷等級

根據云模型的定義，利用正向云發生器，將預警雷達各毀傷等級轉化為對應的云模型，設預警雷達毀傷等級論域滿足=[0,1]，各毀傷等級對應的論域區間分別為：無毀傷=[0,01]，輕度毀傷=[01,03]，中度毀傷=[03,05]，重度毀傷=[05,07]，失能=[07,10]。

云模型滿足正態分布，設預警雷達某毀傷區間為[,]，毀傷區間云模型數字特征參數為=(+)2、=(-)6、=10。 因此，預警雷達毀傷區間對應的毀傷云數字特征如表4所示。

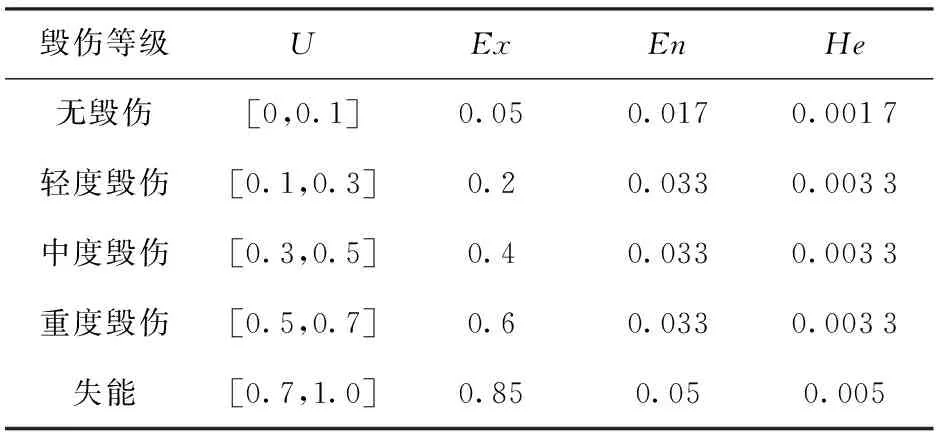
表4 預警雷達毀傷云數字特征

各毀傷等級對應云模型如圖6所示。

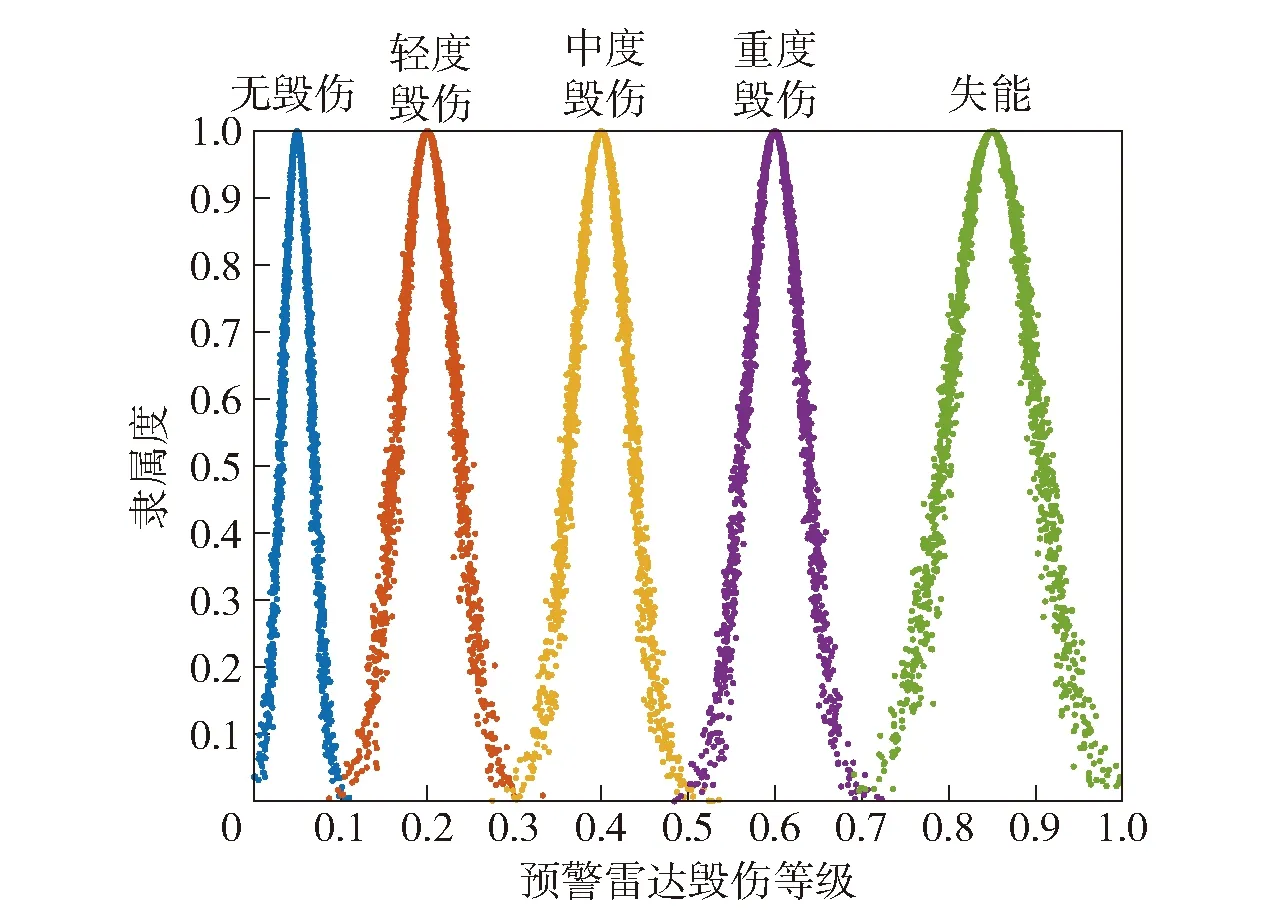
圖6 預警雷達毀傷等級云模型Fig.6 Damage level cloud model of early warning radar

3 確定條件概率

實際問題中，在給定貝葉斯網絡拓撲結構的前提下，確定各節點條件概率的方法主要是通過對已有數據信息進行訓練得到條件概率信息。而在利用統計信息生成條件概率表時，常會出現因統計信息缺失而無法訓練得到完整的條件概率表。 DS/AHP方法結合了DS與AHP法，將不完整的專家經驗信息進行表達、融合，有效地降低了傳統專家經驗法推斷結果的不確定性。專家決策判斷標準如表5所示，與傳統AHP法相比，DS/AHP法避免了選擇方案比較與模型一致性檢驗等工作，專家可就熟悉的方案進行判斷，對不確定的方案則可以選擇放棄。

表5 專家決策判決標準

本文因各節點狀態都在3個以上，因此將節點二元狀態條件概率的確定方法擴展到多元狀態，研究節點多元狀態下條件概率的取值方法。

設表示貝葉斯網絡節點的所有可能取值集合，內節點各種狀態發生的可能性互斥，則為節點的識別框架。若的冪集構成了集合2，??。定義函數：2→[0,1]，若滿足條件：

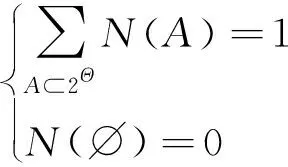
(18)

則()為上的基本信度分配函數(BPA)。根據Dempster規則，可對識別框架上兩個相互獨立的BPA進行合成：

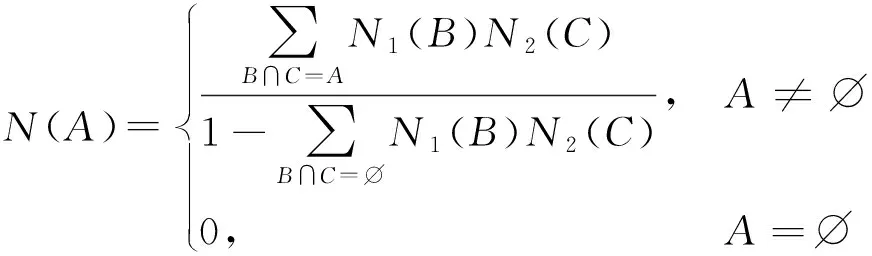
(19)

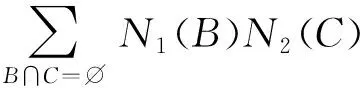
假設邀請專家參與條件概率賦值。位專家分別記為，，，…,，從維屬性(，，，…,)對條件概率組合方案,,…,(∈2，=1,2,3,…,)進行相對于的重要度判斷，構建基于專家評判的屬性知識矩陣，如表6所示。

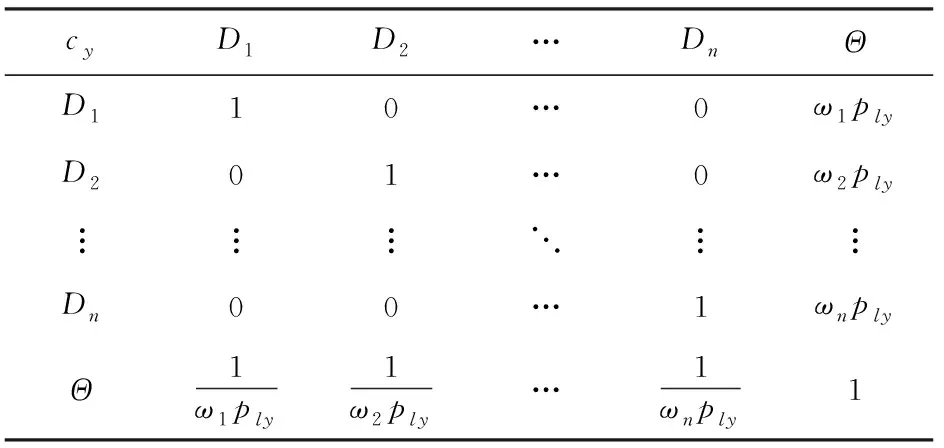
表6 基于專家el評判的屬性cy知識矩陣

表6中：=1時表示方案自身進行比較，=0時表示方案未進行比較；表示屬性條件下專家的權重；表示相對于的對比系數。

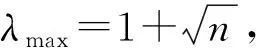
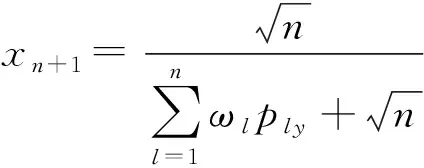
(20)

4 算例分析

我方偵測到敵反導體系的預警探測系統有4部相同型號的預警雷達，工作參數如表7所示。

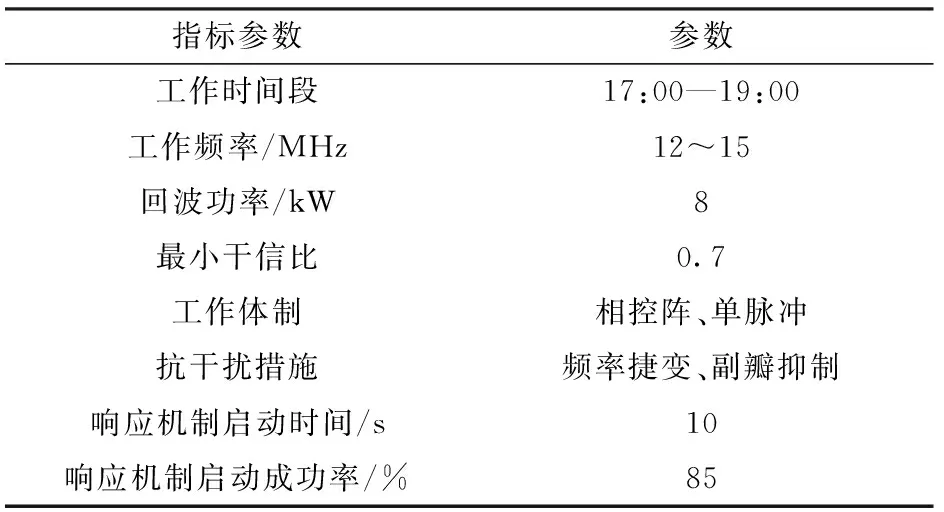
表7 預警雷達工作參數

擬對預警雷達實施干擾毀傷，共有4部干擾機，采用“一對一”模式分別對4部預警雷達實施干擾，干擾機工作參數如表8所示。

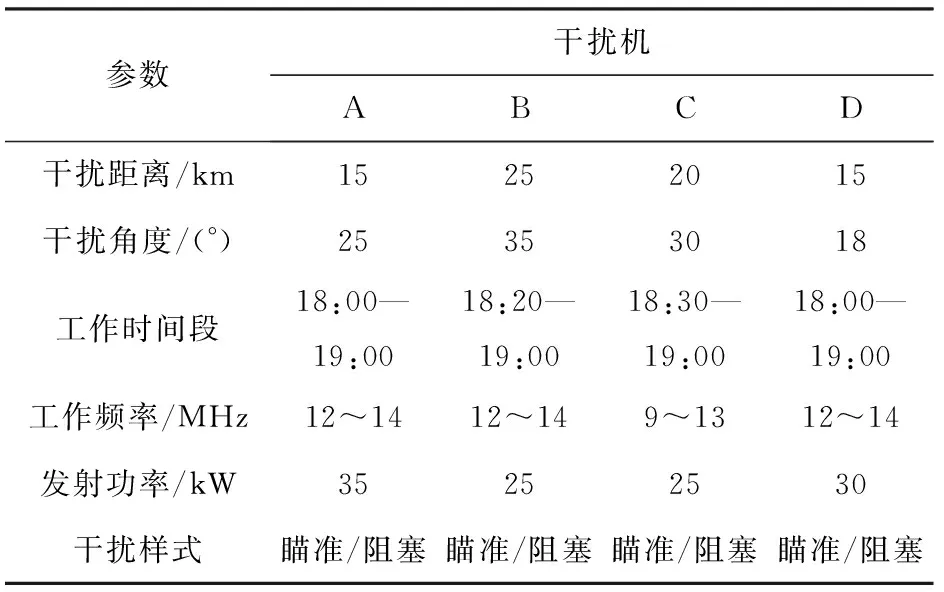
表8 干擾機工作參數

4.1 確定指標變量

結合2.2與2.3節內容，計算各評估指標體系變量并進行歸一化處理，如表9所示。

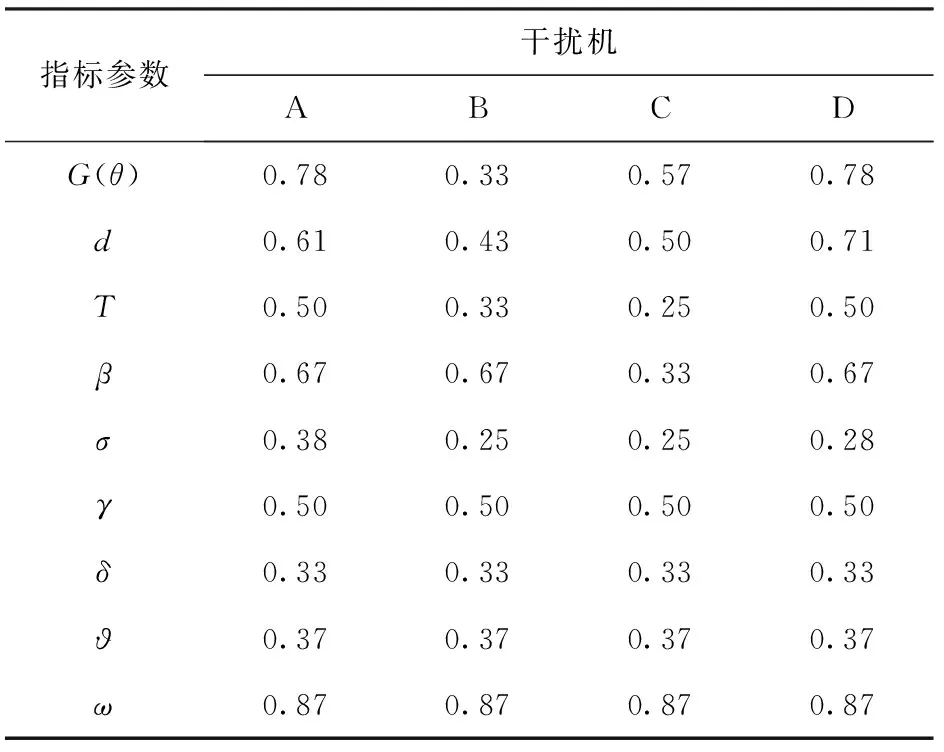
表9 歸一化后的評估指標體系變量

4.2 進行推理運算

咨詢4位技術專家，按照表5提供的專家決策判斷標準分別計算圖2中各個事件相對于子節點所處狀態偏好程度的專家知識矩陣。假設參加評判工作的專家權重分別為=030、=035、=020與=015。 以預警雷達毀傷程度處于重度毀傷狀態為例，建立干擾機攻擊能力的專家知識矩陣，如表10～表13所示。

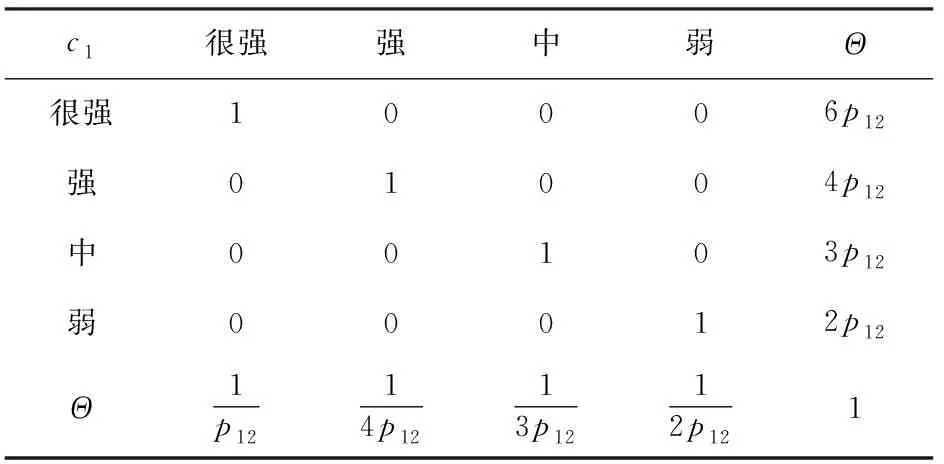
表10 以專家1偏好建立的知識矩陣B1

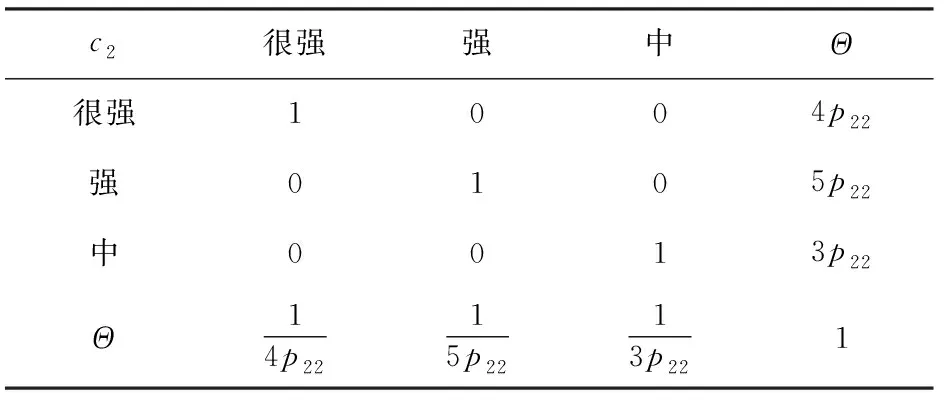
表11 以專家2偏好建立的知識矩陣B2

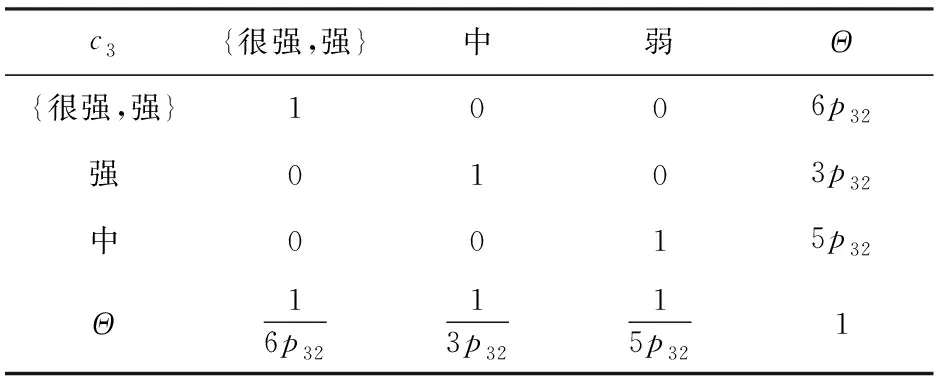
表12 以專家3偏好建立的知識矩陣B3

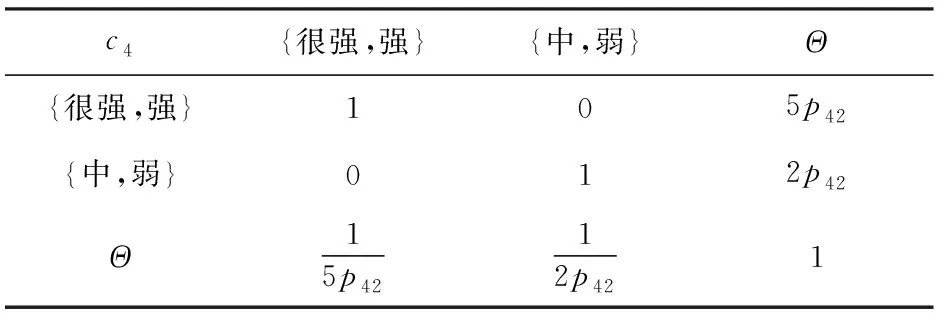
表13 以專家4偏好建立的知識矩陣B4

由(19)式與(20)式求出各證據的基本概率分配：(很強)=028，(強)=018，(中)=014，(弱)=009，()=031；(很強)=023，(強)=030，(中)=018，()=029；({很強，強})=027，(中)=013，(弱)=022，()=038；({很強，強})=({中，弱})=012，()=057。

031，按照(18)式Dempster規則，對信度函數進行合成可得事件的BPA值如表14所示。

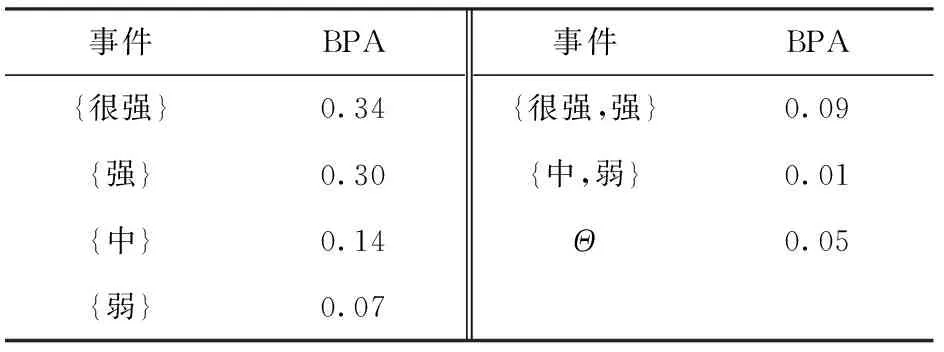
表14 信度函數合成后得到的各事件的BPA值

由表14可知，干擾機攻擊能力為很強的概率為0.34+0.09/2=0.38，為強的概率為0.30+0.09/2=0.35，為中的概率為0.14+0.01/2=0.15，為弱的概率為0.07+0.01/2=0.07，不確定度為0.05。

同理，可得到其余子節點的BPA值，進而得到各子節點的條件概率值。

由于事先沒有特殊說明，可假設預警雷達毀傷程度的先驗概率為{0.2，0.2，0.2，0.2，0.2}。將父節點先驗概率與各子節點條件概率值輸入貝葉斯網絡；將表8中的數據進行云模型轉換后由隸屬度—概率轉換公式將隸屬度轉換為概率，以證據的形式輸入貝葉斯網絡。利用MATLAB軟件的BNT工具箱建立如圖7所示貝葉斯網絡模型。

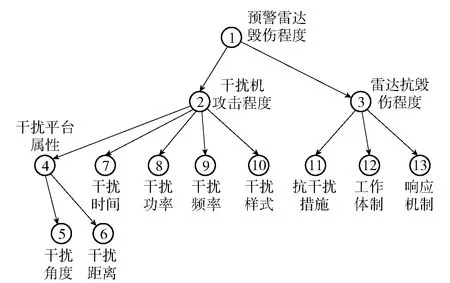
圖7 BNT工具箱建立的貝葉斯網絡模型Fig.7 Bayesian network model based on BNT toolbox

4.3 結果分析

初始化貝葉斯網絡并通過聯結樹法進行貝葉斯網絡推理，得到預警雷達在干擾機作用下處于不同毀傷程度的概率如表15所示，圖8為各毀傷概率對應的分布直方圖。

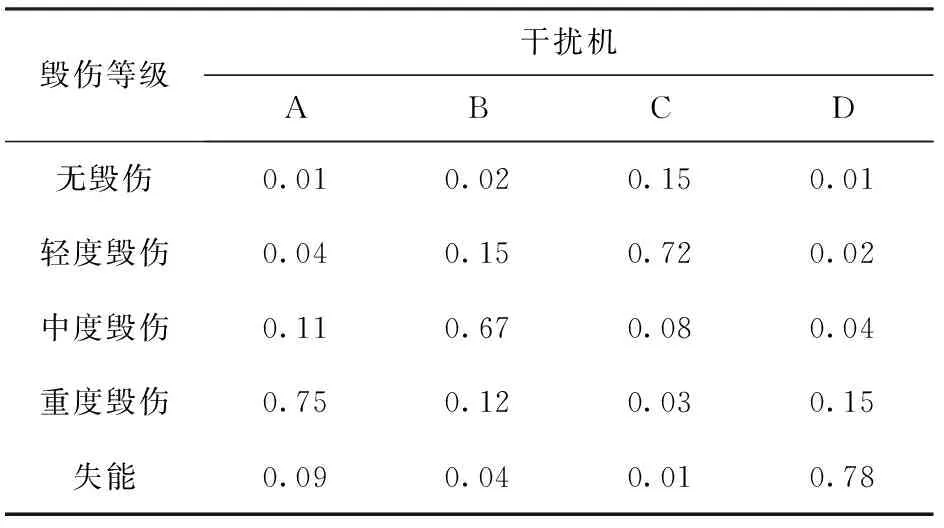
表15 預警雷達不同毀傷等級概率

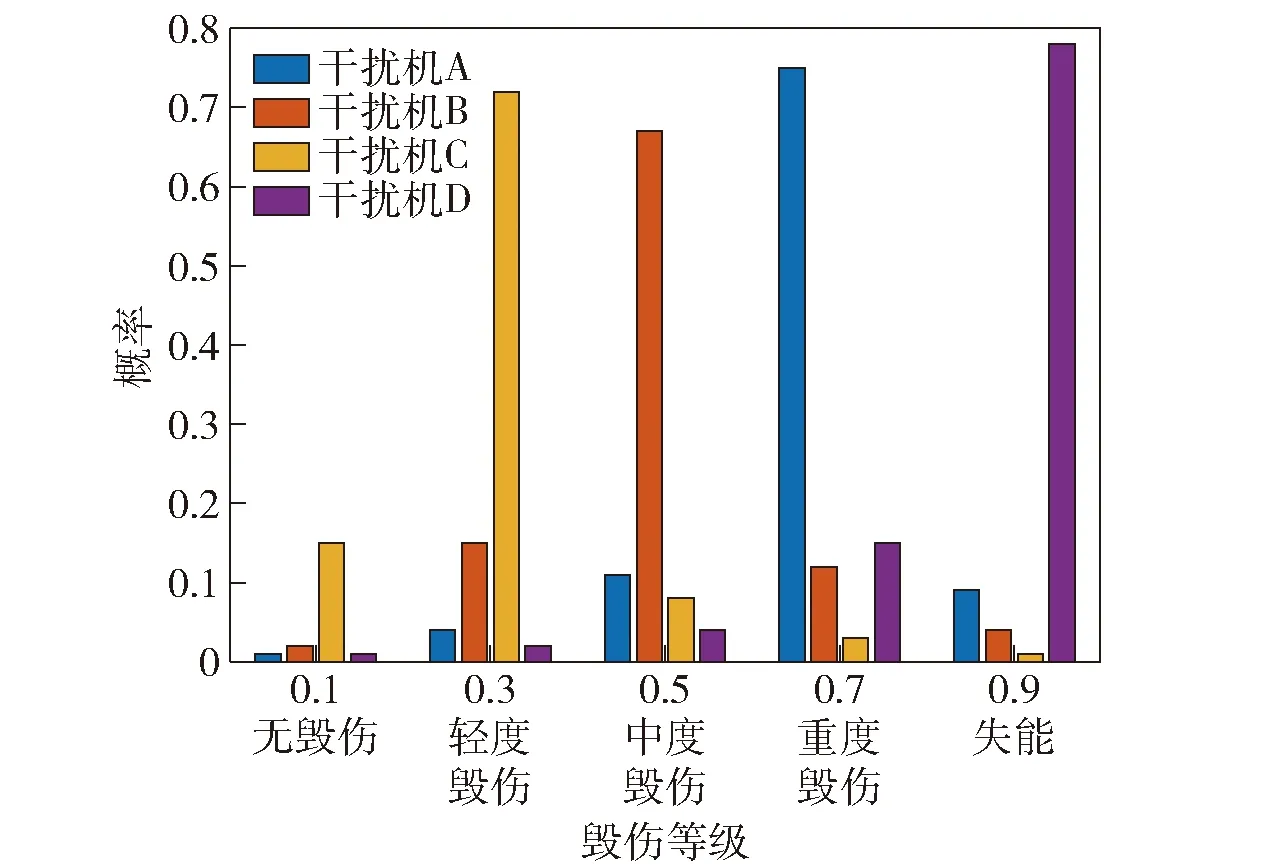
圖8 各毀傷概率對應的分布直方圖Fig.8 Distribution histogram of each damage probability

分析表15可知：在干擾機A攻擊下，預警雷達屬于重度毀傷等級的概率為0.75；在干擾機B攻擊下，預警雷達屬于中度毀傷等級的概率為0.67；在干擾機C攻擊下，預警雷達屬于輕度毀傷等級的概率為0.72；在干擾機D攻擊下，預警雷達屬于失能狀態的毀傷等級分別為0.78。

分析表15的計算結果可知，干擾機A、干擾機D 對預警雷達的毀傷效果優于干擾機B、干擾機C，而由表8可知，干擾機A、干擾機D在干擾距離、發射功率等方面均優于干擾機B、干擾機C，這也說明了本文提出方法的計算結果與所給數據的一致性。干擾機D與干擾機A的攻擊距離更接近于其最小壓制距離，同時二者的干擾功率較之干擾機B與干擾機C更大，在干擾功率上更容易形成壓制。

同時，干擾機A的干擾角度大于干擾機D，干擾機D的發射功率小于干擾機A，若要比較干擾機A與干擾機D對預警雷達的干擾效果，僅僅通過表8中的數據是無法做出判斷的，而通過本文提出的算法可以推理得出干擾機D對預警雷達的干擾效果優于干擾機A。

雖然干擾機A的干擾功率大于干擾機D，但干擾機D的攻擊角度大于干擾機A，干擾機D對預警雷達的毀傷效果更佳，可見干擾機D較之干擾機A在干擾角度方面的優勢更為顯著。

同理，干擾機C較之干擾機B在干擾距離、干擾角度方面有優勢，但干擾機B在工作時間段、工作頻率方面較之干擾機C有優勢，因此，僅僅通過對比表8數據顯然也無法比較干擾機B與干擾機C對預警雷達的干擾效果。

雖然干擾機C較之干擾機B在干擾距離、干擾角度等方面更有優勢，但在工作時間段、工作頻率方面，干擾機B的性能較之干擾機C的優勢更加顯著，所以干擾機B對預警雷達的毀傷程度更高。

根據推理運算，可得到各干擾機對預警雷達的毀傷效果從好到次的排序為干擾機D、干擾機A、干擾機B、干擾機C。 在實際作戰中，可根據干擾機的工作參數估算對預警雷達的工作效果，以為作戰分析提供可行依據。

如圖9所示，可得到干擾機相對于各毀傷等級的綜合毀傷云圖，圖9中藍色部分對應圖6云模型。干擾機A、干擾機B、干擾機C、干擾機D的毀傷值分別為0.67、0.35、0.14與0.83。通過對比相似面積分別確定干擾機A、干擾機B、干擾機C、干擾機D的毀傷等級為重度毀傷、中度毀傷、輕度毀傷與失能，與之前分析能夠匹配。

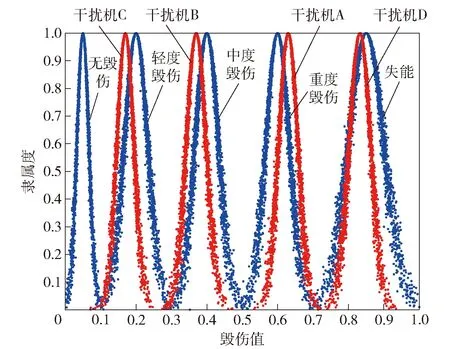
圖9 綜合毀傷云圖Fig.9 Comprehensive damage cloud map

4.4 算法有效性分析

為驗證本文方法的有效性，將貝葉斯網絡法、模糊綜合評判法、云重心評判法、云貝葉斯網絡法用于目標毀傷效果評估，將各類評估方法所得結果與算例結果進行對比分析，結果如表16所示。

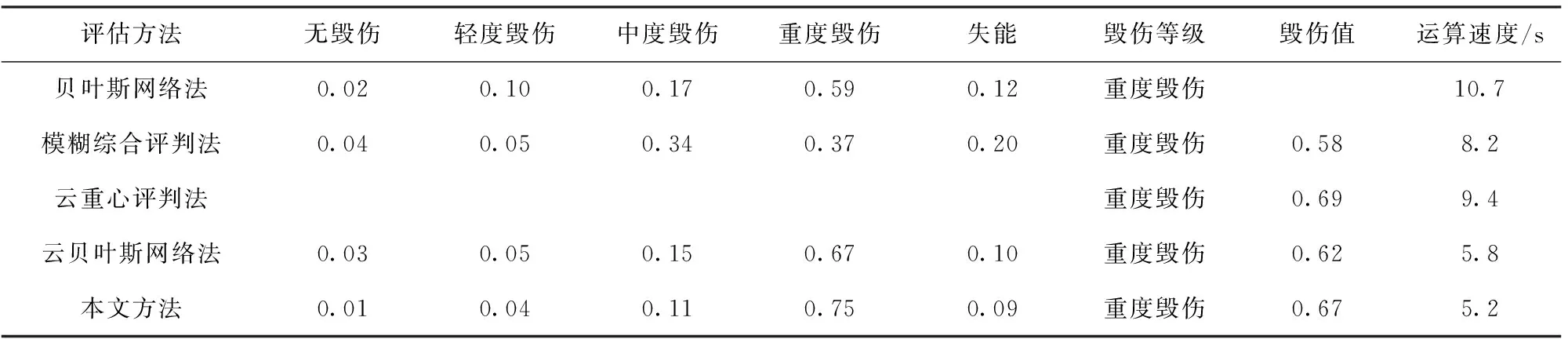
表16 各類評估方法的結果對比

由于篇幅限制，表16只列舉了各類算法在預警雷達受干擾機A攻擊下的運算結果。分析結果可知：

1)5種算法求得的毀傷等級均為重度毀傷，證明了本文算法的合理性。

2)貝葉斯網絡法利用模糊理論實現了貝葉斯網絡中節點隸屬度向貝葉斯推理概率的轉化，雖然得到了預警雷達屬于各個毀傷等級的概率，但無法求出毀傷值。由于概率是不確定性的體現，若無毀傷值做對照，則所求結果可靠性不夠。

3)模糊綜合評判法求得了預警雷達屬于各毀傷等級的概率與毀傷值，但由于中度毀傷與重度毀傷的概率值差別不大，故直接判定預警雷達屬于重度毀傷的準確性還值得商榷。

4)云重心評判法求得的毀傷值與本文所得的毀傷值相近，但無法得到預警雷達屬于各毀傷等級的概率。若不與其他毀傷等級做比較而僅憑毀傷值判斷毀傷等級屬于重度毀傷，則求解過程中信息的單一性將導致判斷誤差的增大。

5)云貝葉斯網絡法求得的預警雷達毀傷等級與毀傷值均與本文算法相近，進一步印證了本文算法的合理性，但其在確定條件概率時僅依靠實驗數據，若實驗數據存在缺失或較大誤差，則所得結果的偶然性必然增加。

6)本文方法的運算速度為5.2 s，與云貝葉斯網絡法的運算速度接近，相對于貝葉斯網絡法、模糊綜合評判法、云重心評判法有較明顯的優勢。

5 結論

本文以貝葉斯網絡模型為基礎，通過引入云模型理論，建立了基于云貝葉斯網絡的預警雷達毀傷效果評估模型，在此基礎上，采用DS/AHP法確定評估模型各節點的條件概率值，推理運算得到各毀傷等級概率。得出以下主要結論：

1)本文方法得到了預警雷達屬于各毀傷等級的概率值，判定了預警雷達的毀傷等級并確定了對應的毀傷值。綜合而言，本文方法在計算合理性與準確度方面均優于文中提到的其他方法。

2)本文方法在運算速度上也較之其他方法具有一定的優勢，運算速度分別較云貝葉斯網絡法、貝葉斯網絡法、模糊綜合評判法、云重心評判法提升了11.5%、105.8%、57.7%、80.8%。

3)本文方法為后續研究工作明確了方向，使用的研究思路可擴展于研究不同工況下干擾機對預警雷達實施“多對一”模式干擾、“一對多”模式干擾時的毀傷效果，還可將本文研究思路推廣到對其他目標毀傷的研究工作中，分析組合攻擊模式下體系目標毀傷效能的變化情況。