多線引入的軌道電路橫向連接位置優化計算方法
孫 哲
(中鐵工程設計咨詢集團有限公司,北京 100055)
1 概述
目前,對于設有軌道電路的電氣化復線鐵路,主要采用橫向連接作為連通牽引回路,平衡上、下行線路牽引回流的主要裝置[1]。橫向連接分為簡單和完全兩種類型。簡單橫向連接由空扼流變壓器或空心線圈、橫向連接線等構成;完全橫向連接由高阻抗扼流變壓器、橫線連接線、中心接地線及吸上線等構成[2]。
在橫向連接的工程設計中,現行規范及相關文件[3-6]從頻率、間隔長度、連接線距離等多個角度對橫向連接的設置進行了規定。其位置設計需考慮大量的約束條件,人工計算的工作量大、準確度不高。為此,楊帆[7]綜合考慮了技術規范條件和投資控制,提出了基于回溯法的軌道電路橫向連接設置方法,實現了橫向連接位置的計算。但此方法未考慮存在并行區段以及某處橫線連接上、下行扼流變壓器不在同一里程的情況,且采用的回溯法主觀性太強,不具備通用性。
現今,我國多個新建鐵路項目存在多條聯絡線或走行線接軌引入正線情況。計算此種情況下的橫向連接位置時,需同時考慮正線、引入線橫向連接的設置,進一步增加了橫向連接位置工程計算復雜度。為此,提出一種考慮多線引入情況的橫向連接位置數學模型,并采用基于多目標粒子群的優化方法,綜合考慮投資成本及回流性能,以實現此種情況下橫向連接位置優化計算。
2 多目標優化問題相關概念
在實際優化問題中,存在著大量具有多個目標函數的情況。解決此類問題,一般可通過線性加權,將其轉化為單一目標函數來求解[8]。然而,各目標函數之間往往相互沖突且屬于不同量綱,直接線性加權的方法魯棒性較差。為此,許多學者對以求解Pareto最優解集為目的的多目標優化方法進行了研究[9-11]。
2.1 多目標優化問題基本概念
對于一個求最小值的多目標優化問題[12],可用如下數學表達式表述
miny=f(x)=[f1(x),f2(x),…,fm(x)]

(1)
式中,x=(x1,x2,…,xn)∈Rn為由n個變量組成的決策向量;y=(y1,y2,…,ym)∈Rm為由m個目標函數構成的向量;gk(x)(k=1,2,…,p)與hl(x)(k=1,2,…,q)分別表示需滿足的p個不等式約束和q個等式約束。
以求解最小值的兩目標優化問題為例,若x1、x2為可行域中的兩個解向量,則當且僅當滿足如下條件時,稱x1支配x2,記做x1x2。
(2)

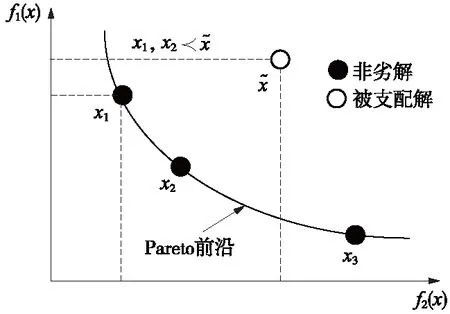
圖1 支配與Pareto前沿
2.2 基于擁擠距離的多目標粒子群
粒子群算法(PSO)是一種基于群體智能的進化式算法,它通過粒子速度和位置更新,迭代出種群歷史最優和全局最優,具有收斂速度快、方便計算機實現等特點[13]。
多目標粒子群算法(MOPSO)將PSO的基本原理應用于多目標問題中,通過構造個體歷史Pareto最優集Gbest和種群全局Pareto最優集Pbest,以期求解出分布均勻、最靠近真Pareto前沿的非劣解集[14-16]。在迭代過程中,通過擁擠度排序[17-18],找出Gbest、Pbest中稀疏度最大的解作為個體最優解gbest和全局最優解pbest,以實現解的不斷優化,算法流程如圖2所示。

圖2 MOPSO算法原理
3 橫線連接位置優化問題數學描述
3.1 橫向連接位置模型
(1)正線橫向連接位置模型
在實際工程應用中,簡單、完全橫向連接的基本構件均為一對扼流變壓器和一條橫向連接線。因此,若某條鐵路正線設置nz個橫向連接,則各個橫向連接里程由小到大依次構成nz維向量Hz,表示為

(3)
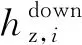

(4)
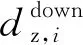
由式(3)、式(4)可得,正線第i對橫向連接的里程可描述為
(5)
(2)引入線橫向連接位置模型
對于工程中存在聯絡線、走行線等引入線的情況,因引入線會通過正線上的接軌點接入正線,則應建立引入線橫向連接位置模型,并與正線橫向連接位置統籌考慮。
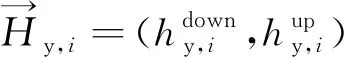
(6)
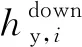


(7)
則引入線上第i對橫向連接的里程均可由同方向之前橫向連接之間的距離描述,即
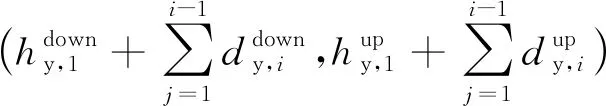
(8)

(9)
(10)
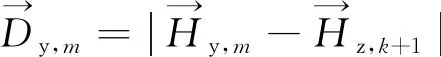
(11)
3.2 約束條件
ZPW-2000A及ZPW-2000R軌道電路工程設計說明中對橫向連接的設計位置進行了規定,將其數學描述如下。
(1)相鄰橫向連接間距約束
根據規范,相鄰兩個橫向連接應至少有一個為完全橫向連接,且橫向連接設置間隔應滿足接觸網回流線的間隔要求,則對于同方向相鄰橫向連接均為完全橫向連接的情況,應滿足

(12)
式中,dF-F為線路連續兩個橫向連接均完全橫向連接時,其同方向的兩個扼流變壓器的間距;minRd為線路最低道床電阻。
對于線路上某一簡單橫向連接,由于兩處相鄰完全橫向連接間最多可設置1處簡單橫向連接,且簡單橫向連接與完全橫向連接間的距離不小于1 000 m,則有
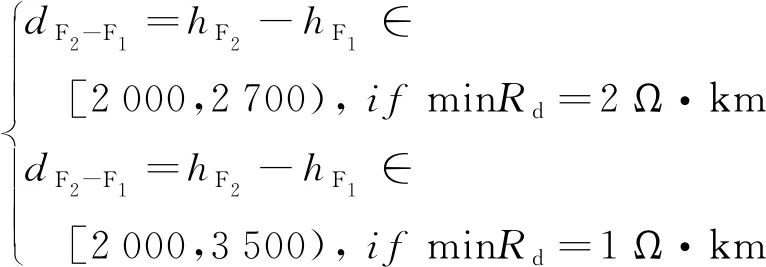
(13)
同時,若minRd=2 Ω·km,滿足
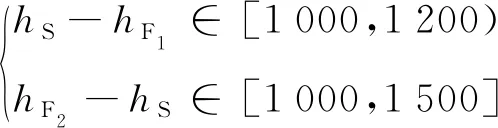
(14)
若minRd=1 Ω·km,滿足


(15)
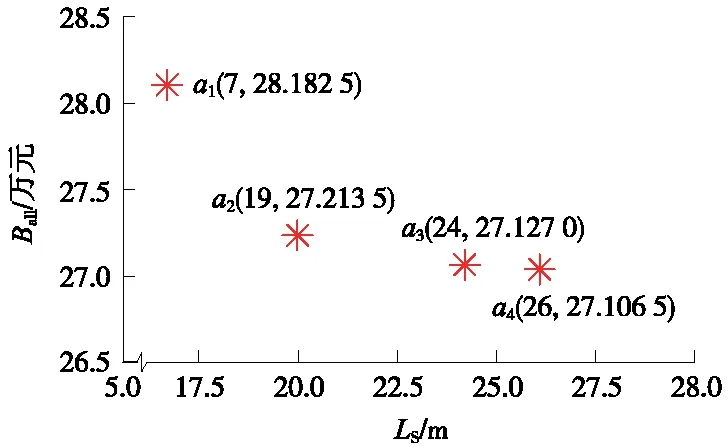
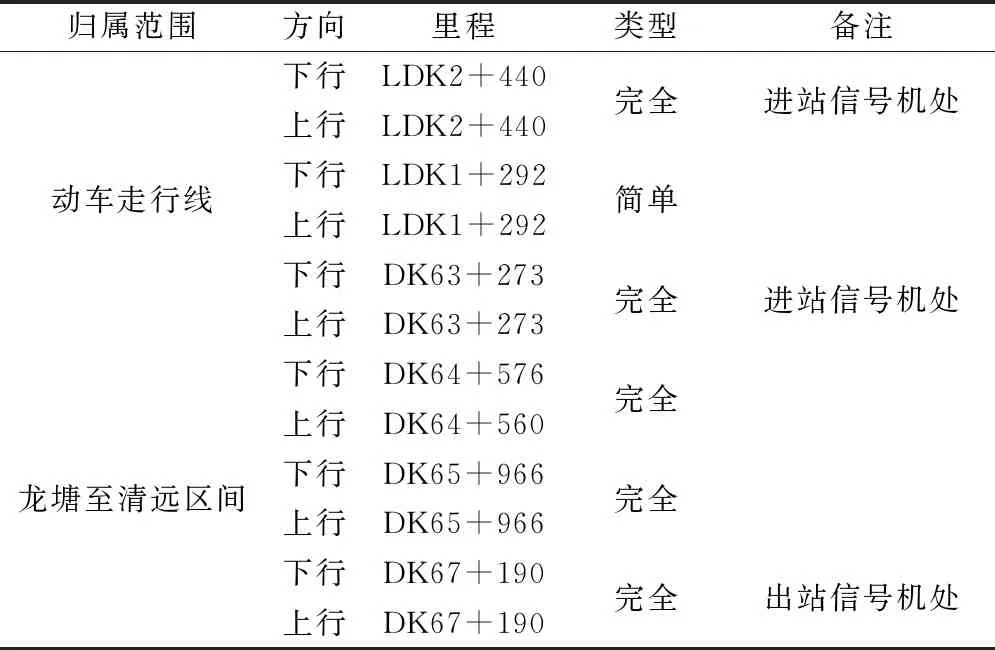
式中,hS、hF1、hF2分別為簡單橫向連接及其相鄰兩個完全橫向連接同方向上扼流變壓器的位置,且hF1 同時,橫向連接線不應超過100 m,則有 (16) 式中,φH為同一處橫向連接線允許最大里程差,可適當縮小取值,一般取φH=50 m。 (2)補償電容、調諧單元距離約束 對于正線或引入線上某一處橫向連接的扼流變壓器,設其所在軌道電路區段有m個補償電容、2個空心線圈,且里程從小到大依次為 K1,C1,C2,…,Cm,K2 (17) 若該扼流變壓器與機械空心線圈處于同一位置,則可利用該空心線圈處的扼流變壓器,無需新設,并滿足:hi=K1或hi=K2,hi為該扼流變壓器的位置。 否則,需新設扼流變壓器,且新設扼流變壓器相對于補償電容的距離不應小于10 m、相對于空心線圈的距離不應小于50 m,滿足 (18) 式中,φC、φK分別為考慮施工誤差而設置的橫向連接扼流變壓器相對于補償電容、空心線圈的余量。 (3)頻率條件約束 相鄰兩個橫向連接不能接入同一軌道電路區段,即滿足 st:hi+1-hi≥lhi (19) 式中,hi、hi+1為相鄰兩處橫向連接同方向線路上扼流變壓器的位置;lhi為hi位置處扼流變壓器所在軌道電路的長度。 (4)牽引所亭回流線約束 對于距離牽引供電專業牽引所亭位置最近的一組完全橫向連接,根據供電專業相應要求,其扼流變壓器應設于牽引變電所亭附近一定范圍內,即滿足 (20) 在滿足上述約束條件下,目標函數應考慮工程的經濟性、可實施性及可靠性,為此,將目標函數可設置成如下幾類。 (1)工程總投資預算應盡可能低 根據式(3)~式(11),則有 (21) 對于正線或引入線上任一處完全橫向連接,若兩端均需增設扼流變壓器和吸上線,則其預算Bi可描述為 (22) 式中,Pe為扼流變壓器的單價;le為兩端空扼流變壓器連接電纜的長度;Pl為連接電纜單位長度預算;Pg為接地預算;δ為線路間距,一般取5 m。 若一端滿足設于機械絕緣節空心線圈處,則其預算Bi可描述為 (23) 若兩端均滿足設于機械絕緣節空心線圈處,則其預算Bi可描述為 (24) 對于處于牽引變電所亭最近的完全橫向連接,還應考慮回流線的預算,此時Bi可描述為 (25) 式中,PS為單位長度回流線預算;lS為此處應設回流線長度,此處僅考慮牽引變電所亭與橫向連接的相對里程差為回流線長度;S為牽引變電所亭的位置。 對于正線或引入線上任一組簡單橫向連接,因無需接地處理,則其預算Bi可以描述為 (26) 特別地,對于單線橋梁地段,上述橫向連接線長度可設置為0。 (2)連接牽引所亭的回流線的線纜長度盡可能短,使線纜電阻盡量小,線路具備良好的回流性能。即滿足 (27) 在工程設計中,正線上第一個和最后一個橫線連接位置是可以提前確定的,若兩者間距為Lz,且正線所有完全、簡單橫向連接的個數分別為nz,F、nz,S(nz,F,nz,S∈N),則Lz、nz,F、nz,S之間滿足 Lz=(nz,F-nz,S-1)·dF-F+nz,S·dF2-F1 (28) 由此可得 (29) 聯合不等式(12)、式(13),進一步可得 (30) 例如:Lz=20 km,minRd=2 Ω·km,若nz,S=0,則nz,F∈(14.1,17.9],即nz,F取值可以為15,16,17;若nz,S=1,則nz,F∈(13.13,17.5],即nz,F取值可以為14,15,16,17。 對于引入線,其橫向連接設置范圍Ly、完全橫向連接個數ny,F和簡單橫向連接個數ny,S同樣滿足上述關系。為方便描述,將nz,F、ny,F能取到的最小值和最大值依次表示為Mz,1、Mz,2、My,1、My,2。 由于完全橫向連接具有更好的回流性,工程中應盡量全部設置為完全橫向連接。因此,在求解橫向連接Pareto最優位置集Gbest的過程中,可以先將nz,S、ny,S設置為0,求解此情況下的Pareto最優位置集Gbest。若此時Gbest=?,則將nz,S的個數依次加1,直到Gbest≠?。 同時,引入線橫向連接的位置依賴于正線接軌點橫向連接的位置,因此,可先對正線橫向連接位置進行優化,以正線橫向連接Pareto最優化位置集Gz,best中每個非劣解的接軌點附近橫向連接位置來確定引入線橫向連接范圍,再依次對引入線橫向連接位置進行優化。 以正線的橫向連接優化過程為例,算法具體步驟如下。 Step1:確定正線橫向連接布置長度Lz及橫向連接范圍內各補償電容、電氣絕緣節空心線圈、進出站信號機處機械絕緣節、正線股道分割點處絕緣節、各牽引變電所亭里程。 Step2:令nz,S=0,根據式(28)確定Mz,1、Mz,2,并令nz,F=Mz,1。 Step3:根據式(1)~式(4)、式(10)~式(18),初始化本次尋優的正線橫向連接位置種群Pz,0。之后根據式(19)~式(24),采用MOPSO求解此條件下正線橫向連接Pareto位置集Gz,best,并將Gz,best非支配更新至正線橫線連接歷史Pareto位置集Hz,best。 Step4:令nz,F=nz,F+1,重復Step3,直至nz,F=Mz,2。 Step5:此時,若Hz,best=?,則令nz,S=nz,S+1,重復Step2~Step3,直至Hz,best≠?。 Step6:輸出正線橫線連接歷史Pareto位置集Hz,best。 對正線、引入線橫向連接位置依次進行MOPSO優化后,可以得到全線Pareto最優位置集Gbest,再對其進行稀疏度排序,得到最終橫向連接位置最優解。 根據本文提出算法,采用Python語言編寫出基于MOPSO的橫向連接位置優化程序,并以新建廣清城際鐵路區間橫線連接設計為例,對所提算法的有效性進行驗證。 廣清城際鐵路共有1條正線和1條走行線,正線全長38.126 km,設廣州北、石陂、獅嶺、銀盞、龍塘、清遠6站,其中,石陂、銀盞為無配線站;動車走行線全長3.716 km,并在龍塘站DK139+45.37處與正線接軌[19]。正線、引入線涉及本算法的部分信號點數據如表1、表2所示。 表1 廣清城際鐵路正線信號點數據 表2 廣清城際鐵路動車走行線信號點數據 該線路區間僅有1處設有回流線的牽引變電所,位于DK64+557處。同時,全線共有8處斷鏈位置,如表3所示。 表3 廣清城際鐵路全線斷鏈位置 將上述數據輸入本算法程序,并令Pl=10,PS=25,Pe=5 000,Pg=500[20]。經0.48 h算法收斂后,求出的全線橫向連接Pareto最優位置集存在4個最優粒子,如圖3所示。 圖3 廣清城際全線橫向連接Pareto最優位置粒子 各粒子正線、引入線中簡單、完全橫向連接個數如圖4所示。 圖4 Pareto最優粒子中橫向連接個數情況 將a1、a2、a3、a4進行稀疏度排序后,可得出粒子a2為最優解。 最優解a2中,正線包含28處完全橫向連接,其中,5處利用站內機械絕緣節處扼流變壓器,其余23處新設;引入線包含2處完全橫向連接、1處簡單橫向連接,完全橫向連接全部利用站內機械絕緣節處扼流變壓器。因篇幅有限,此處僅列出a2中動車走行線及龍塘至清遠正線區間橫向連接位置,如表4所示。 表4 最優解中部分橫向連接位置 將a2中各個橫向連接位置依次進行檢算,結果表明,本算法計算出的橫向連接位置完全滿足工程設計規范要求。同時,本算法運行時間約為0.5 h,依照工程設計經驗,若采用人工計算方式,將至少需要5 h,能夠提升設計效率近10倍。 通過構建多線引入情況下的軌道電路橫向連接位置模型,將橫向連接的工程計算問題轉化為了多目標數學優化問題,并基于MOPSO提出考慮多線引入情況的橫向連接位置優化計算方法。為驗證算法的有效性,采用Python語言編寫了算法程序,并選取廣清城際鐵路正線及走行線數據對本算法進行了驗證,結果表明,本算法的計算結果完全滿足工程設計要求,并將設計效率提升近10倍。因此,本文算法能夠應用于軌道電路橫向連接工程設計。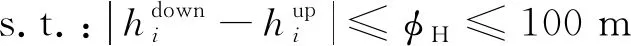
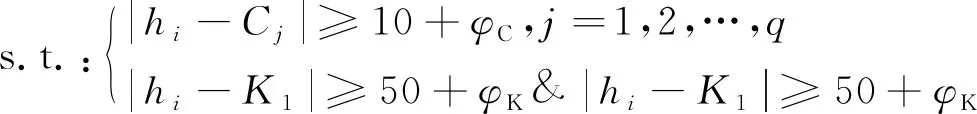
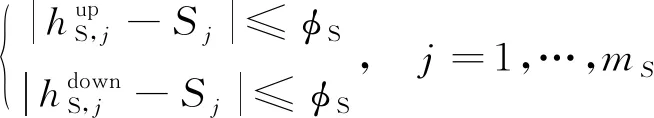

3.3 目標函數
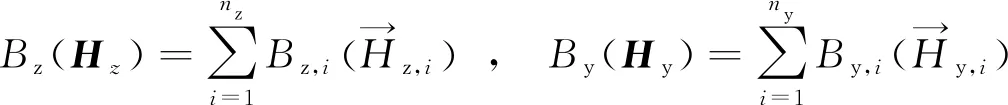



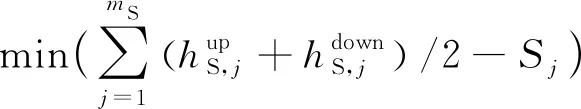

4 橫向連接位置優化算法
4.1 算法總體思路


4.2 算例驗證




5 結論

