不同組合外邊界下多層稠油熱采試井模型研究

瞿朝朝，劉 斌，張 靜，劉玉娟，王立壘

(中海石油(中國)有限公司 天津分公司，天津 300459)

渤海X油田地層原油黏度為50～200 mPa·s，屬于稠油油田，縱向上發育多層儲層，不同層對應外邊界條件不同，層間夾層分布相對穩定，為中高孔、中高滲儲層。國內外學者在研究稠油試井問題時，將稠油處理為冪律流體，并求解其數值解[1-4]。如1980年Ikoku等人研究了考慮井筒儲集和表皮效應的非牛頓冪律流體在多孔介質中的瞬態流動特征,2002年張傳寶等人研究了非牛頓冪律流體試井解釋方法。前人研究表明，稠油黏度受溫度影響顯著，稠油在低溫下黏度大，為非牛頓流體；在高溫下黏度小，為牛頓流體，如張凱等開展的稠油流變特性實驗研究[5-6]。隨后，科研工作者又對稠油油藏復合模型展開了相關研究[7-11]，如2006年劉彬等學者提出的稠油熱采牛頓-非牛頓滲流復合油藏試井解釋模型。但目前不同組合外邊界下多層稠油油藏牛頓-非牛頓雙區復合試井研究較少，海上該類油藏的試井解釋尚無經驗可循。鑒于海上不同組合外邊界條件下多層稠油油藏熱采試井資料解釋困難的問題，本文基于滲流力學理論，建立了不同組合外邊界條件下多層稠油熱采試井模型，運用有限差分算法得到各層井底壓力的瞬時解，并繪制出壓力和壓力導數雙對數理論圖版，旨在為海上該類油藏的試井解釋提供一定理論指導。

1 物理模型建立

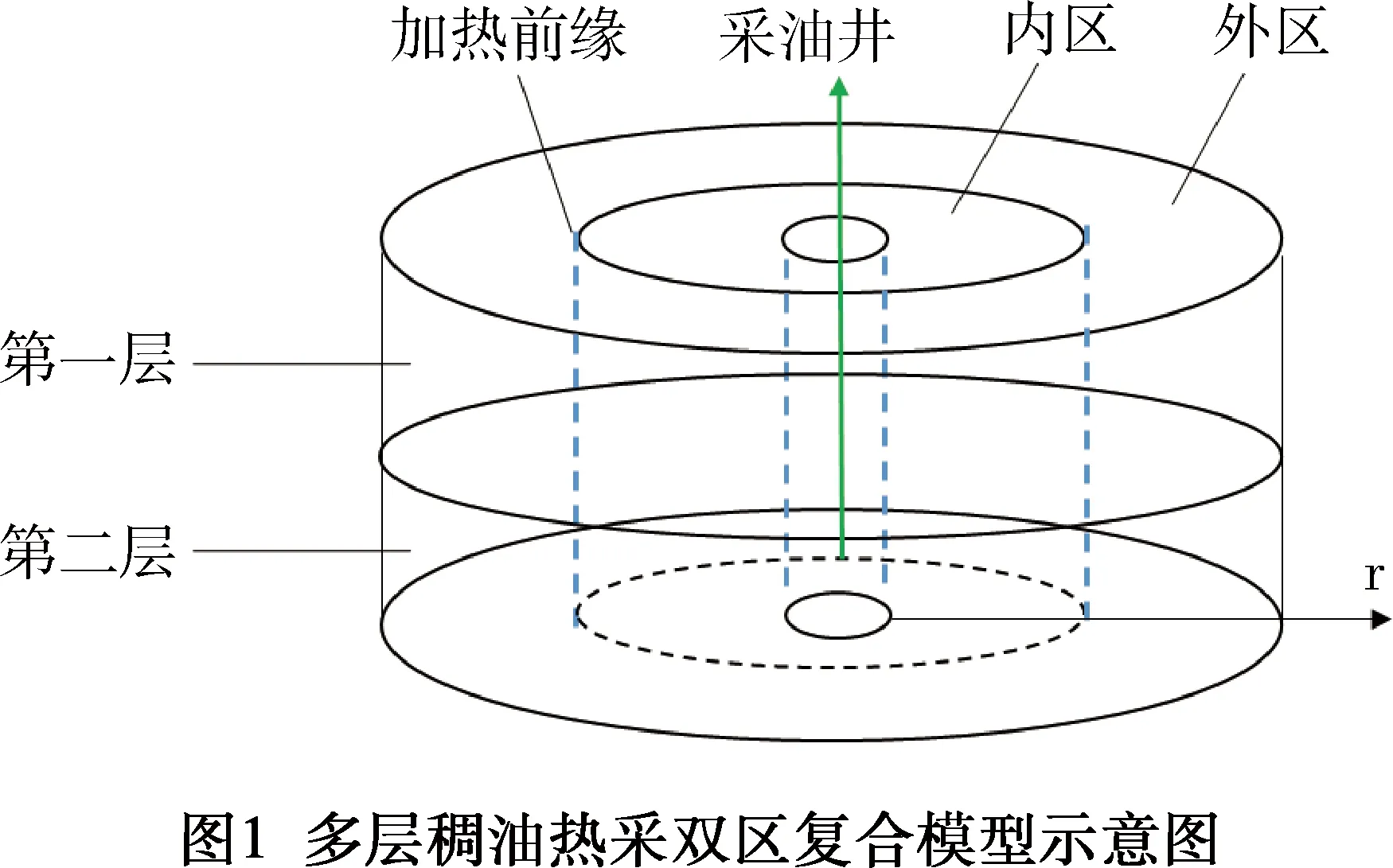
稠油油藏熱采過程中，加熱波及區流體性質不同于未波及區流體，因此將油藏劃分成內外兩區，即加熱波及區和冷油區，雙區復合模型如圖1所示。

假設條件如下:

1)考慮地層中心有1口生產井，縱向鉆遇2層儲層，儲層之間有穩定隔夾層(見圖1)。儲層均質水平等厚，原始條件下地層壓力分布均勻。

2)流體為單相微可壓縮流體，流動滿足達西定律。

3)忽略重力及毛管力影響。

4)考慮井筒儲集和表皮效應影響。

5)兩區滲流界面不存在附加壓力降。

2 試井模型建立及求解

2.1 數學模型

復合模型內區流體為加熱區域，流體可視為牛頓流體，外區流體為稠油溶液，流體可視為非牛頓流體，基于上述物理模型，以滲流力學基本理論為指導，建立不同組合外邊界下多層稠油熱采雙區復合試井解釋數學模型。

滲流方程：

第一層內區：

(1)

式中：r為半徑，m；P11為第一層內區地層壓力，MPa；μ1為內區加熱流體黏度，mPa·s；φ1為第一層孔隙度；Ct11為第一層內區綜合壓縮系數，MPa-1；k11為第一層內區滲透率，10-3μm2；t為時間，s；rm為內區半徑，m。

第一層外區：

(2)

式中：μ2為外區冷油溶液黏度，mPa·s；P12為第一層外區地層壓力，MPa；Ct12為第一層外區綜合壓縮系數，MPa-1；k12為第一層外區滲透率，10-3μm2。

第二層內區：

(3)

式中：P21為第二層內區地層壓力，MPa；Ct21為第二層內區綜合壓縮系數，MPa-1；k21為第二層內區滲透率，10-3μm2；re為邊界半徑，m。

第二層外區：

(4)

式中：P22為第二層外區地層壓力，MPa；Ct22為第二層外區綜合壓縮系數，MPa-1；k22為第二層外區滲透率，10-3μm2。

初始條件：

P11(r,t=0)=P12(r,t=0)=P21(r,t=0)=P22(r,t=0)=Pi

(5)

式中：Pi為原始地層壓力，MPa。

內邊界條件：

(6)

式中：Q為產油量，m3·d-1；B為體積系數；C為井筒儲集系數，m3·MPa-1；Pwf為井底流壓，MPa；h1為第一層地層厚度，m；h2為第二層地層厚度，m；r1為加熱區半徑，m。

(7)

式中：S1為第一層表皮系數；S2為第二層表皮系數。

外邊界條件：

定壓邊界：

P12(r=re,t)=P22(r=re,t)=Pi

(8)

封閉邊界：

(9)

界面壓力、流速相等條件：

P11(r=rm,t)=P12(r=rm,t)

(10)

P21(r=rm,t)=P22(r=rm,t)

(11)

(12)

(13)

2.2 模型求解

基于油藏實際情況，模型考慮了內區流體加熱后的牛頓特性及外區稠油溶液的非牛頓特性，滲流方程變得異常復雜，導致利用常規解析方法求解較困難，本文通過有限差分算法進行時空網格劃分求解方程組，從而得到各層井底壓力的瞬時解。

滲流差分方程：

第一層內區：

(14)

其中：

(15)

式中：i為對空間的離散，i=1，2，…，N；n為對時間的離散,n=1，2，…，K；Δt為離散時間步長，h；Δx為離散空間網格大小，m。

第一層外區：

(16)

其中：

(17)

第二層內區：

(18)

其中：

(19)

第二層外區：

(20)

其中：

(21)

初始條件：

(22)

(23)

內邊界條件：

第一層內邊界：

(24)

第二層內邊界：

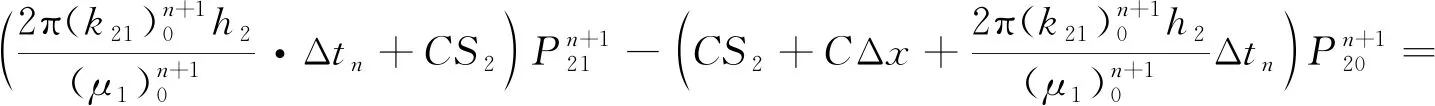
(25)

外邊界條件：

定壓邊界：

(26)

封閉邊界：

(27)

界面壓力、流速相等條件：

第一層：

(28)

第二層：

(29)

其中：I為兩區交界面處位置。

聯立式(14)～式(29)，求解得井底壓力隨時間的變化值：

(30)

3 雙對數曲線特征分析

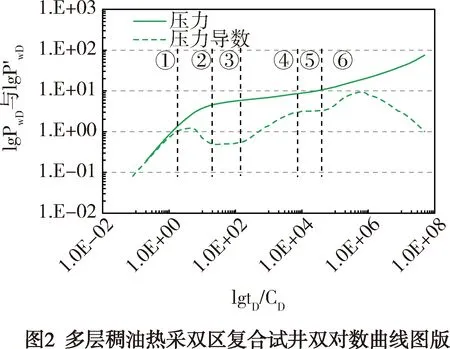
通過對內外邊界條件、初始條件、界面壓力條件及滲流方程組進行差分離散化，并對井底壓力進行量綱歸一化處理，迭代求解得到井底壓力和壓力導數雙對數曲線理論圖版，如圖2所示。

圖2可劃分為6個流動段：①段為井筒儲集段，壓力和壓力導數曲線重合且成45°的直線；②段為井筒向地層過渡段；③段為內區加熱區域擬徑向流段，壓力導數曲線呈現近0.5的水平直線，擬徑向流段結束時刻對應波及距離即為加熱前緣；④段為內區向外區過渡段，壓力波及到外區冷油區，由于外區冷油區的稠油非牛頓特性，壓力導數曲線呈“抬升”狀；⑤段為外區冷油區擬徑向流段，其中內區加熱流體與外區稠油流體滲流達到平衡，表現為近水平直線，導數曲線在縱坐標上的值與冷油區稠油流體黏度相關；⑥段為多層油藏混合外邊界響應流動階段，首先壓力波到達斷層邊界，導數曲線上翹，隨后是定壓邊界的反映，壓力導數曲線呈現平滑下掉趨勢。

采用單一變量法研究加熱半徑、外區稠油黏度、不同混合邊界對雙對數曲線形態的影響。圖3為加熱半徑對雙對數曲線的影響。

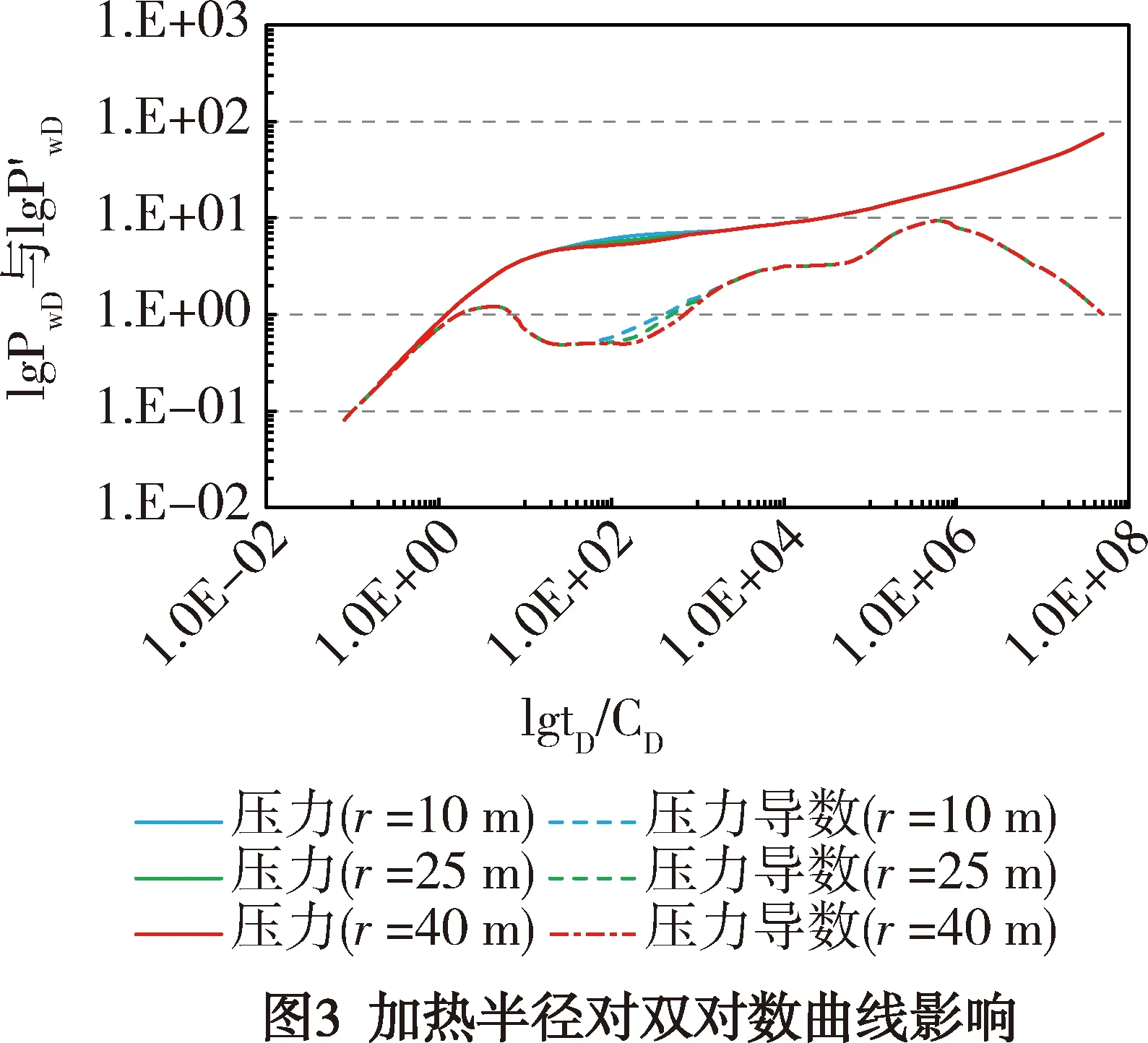
從圖3中可以看出，加熱半徑對內區擬徑向流段的影響較大，加熱半徑越長，內區擬徑向流階段越明顯且持續時間越長。

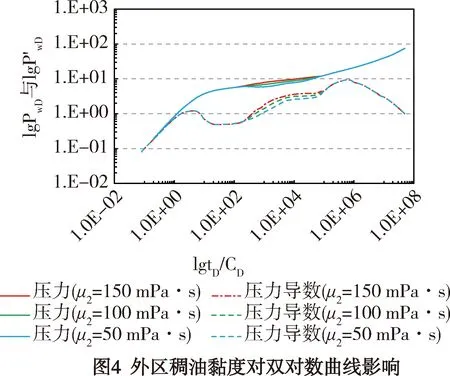
圖4為外區稠油黏度對雙對數曲線的影響。

從圖4中可以看出，外區稠油黏度對內外區過渡段及外區擬徑向流段的影響較大，外區稠油黏度越高，內區向外區過渡段的“抬升”幅度越大，外區擬徑向流階段在縱坐標上對應的值越大。

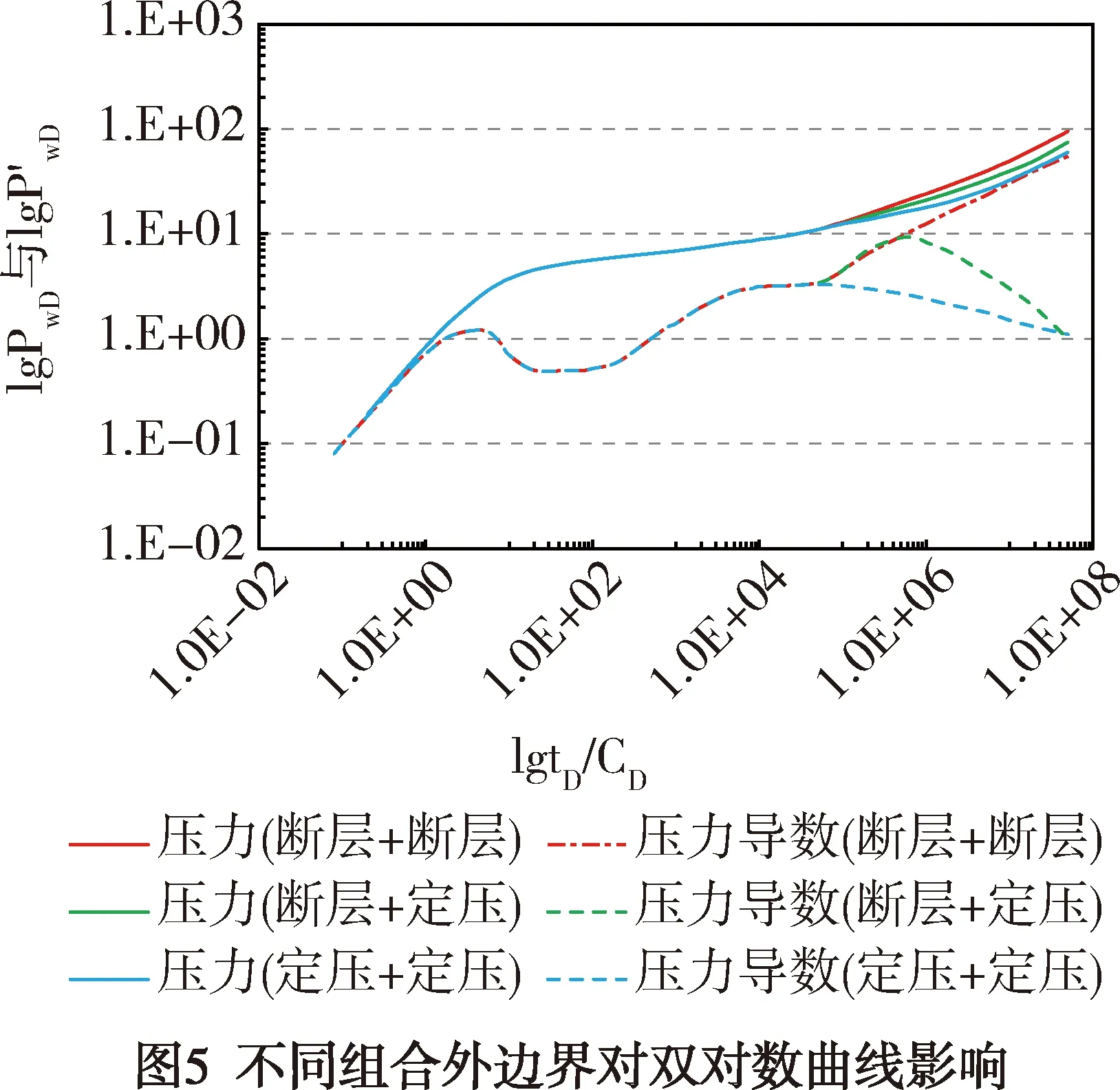
圖5反映不同混合邊界對雙對數曲線的影響。

從圖5中可以看出，當兩層混合邊界條件為斷層+斷層時，導數曲線上翹一直呈上升趨勢；當混合邊界條件為斷層+定壓時，導數曲線先上翹后下掉；當混合邊界條件為定壓+定壓時，導數曲線無上翹段，呈平滑趨勢直接下掉。

4 結論

1)基于滲流力學理論，構建了不同組合外邊界下多層稠油熱采牛頓-非牛頓雙區復合試井數學模型，運用有限差分算法得到各層井底壓力的瞬時解，并繪制出壓力和壓力導數理論圖版。

2)雙對數理論曲線可分為6個不穩定滲流階段，研究了加熱半徑、外區稠油黏度、不同組合外邊界對雙對數曲線的影響。

3)模型可有效指導多層稠油熱采效果及儲層非均質性評價，對海上同類油藏的試井解釋具有一定借鑒意義。