基于深度學(xué)習(xí)的“直線與圓錐曲線位置關(guān)系”復(fù)習(xí)課微設(shè)計(jì)

?山東省臨清市第一中學(xué) 姚繼新

1 引言

直線與圓錐曲線的位置關(guān)系問(wèn)題歷來(lái)是高考的一個(gè)熱點(diǎn)內(nèi)容，更是一個(gè)難點(diǎn)內(nèi)容.為了提高高三復(fù)習(xí)課的效率，筆者選擇2021年4月份山東大聯(lián)考試卷中的第21題作為這節(jié)課的“主打題”.該題是一道典型的直線與圓錐曲線的位置關(guān)系問(wèn)題，特征明顯，思路多樣，于是筆者便“借題發(fā)揮”，在課堂上與學(xué)生就此展開(kāi)了討論.

2 教學(xué)過(guò)程微設(shè)計(jì)片段

(1)求動(dòng)點(diǎn)M的軌跡E的方程；

(2)點(diǎn)P為直線x=3上一動(dòng)點(diǎn)，過(guò)P點(diǎn)作曲線E的切線，切點(diǎn)為Q，線段PQ的中點(diǎn)為N，問(wèn)是否存在定點(diǎn)T，滿足|PQ|=2|NT|？若存在，求出定點(diǎn)T的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由.

感想1：本題是這次聯(lián)考試卷的倒數(shù)第二題，按慣常的思維考慮，應(yīng)屬于“難解”的大題范疇，甚至被有些考生“戰(zhàn)略性放棄”的題目.但就如高考的“解析幾何解答題”一樣，近幾年呈現(xiàn)出“難度下降”的特點(diǎn)，不再那么高不可攀，考生“攻克此題”亦從不可能變?yōu)榭赡?

感想2：本題從出題的角度及形式看，屬于常規(guī)套路.第一問(wèn)是常見(jiàn)的“求軌跡方程”，屬于“白送分”.第二問(wèn)要求考生就定點(diǎn)T的存在性進(jìn)行探索，這種設(shè)計(jì)相較很多題目讓考生直接“求定點(diǎn)T的坐標(biāo)”的設(shè)計(jì)增加了迷惑性，對(duì)考生有明顯的思維上的干擾(畢竟考生還并不是非常確定“定點(diǎn)T”就一定存在)，考查學(xué)生的數(shù)學(xué)探究能力，符合當(dāng)前考查學(xué)生學(xué)科核心素養(yǎng)的命題導(dǎo)向.

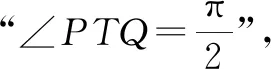
生1：根據(jù)直線與橢圓的位置關(guān)系常用方法，聯(lián)立方程組，根據(jù)相切關(guān)系可以設(shè)點(diǎn)依次求解.

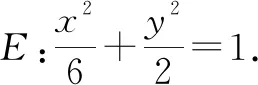
(2)由題意可知直線PQ的斜率一定存在，設(shè)直線PQ的方程為y=kx+m(m≠0)，Q(x0,y0).

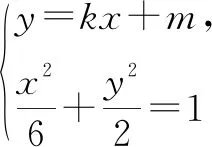
Δ=36k2m2-12(1+3k2)(m2-2)=0，

化簡(jiǎn)得

m2=2(3k2+1).

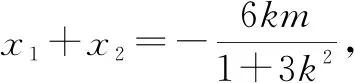
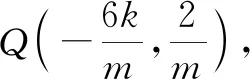
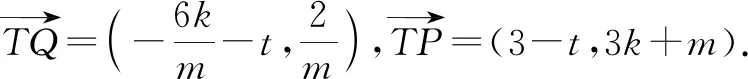
師：生1的解法非常好，是一個(gè)非常典型的解法，也可以算作是通性通法了.該方法的好處在于思路清晰，邏輯嚴(yán)密，便于方法的展開(kāi)，但缺點(diǎn)也很明顯，就是運(yùn)算量偏大，過(guò)程稍顯“繁瑣”.大家再想一想，能否讓過(guò)程變得更簡(jiǎn)捷？

生2：如果我們聚焦于“PQ是橢圓的切線”這個(gè)條件，則可以簡(jiǎn)化第二問(wèn)的解題過(guò)程.

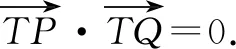
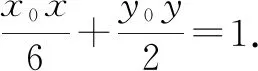
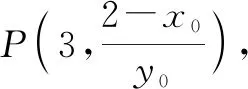
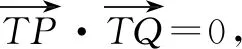
這時(shí)候，老師發(fā)現(xiàn)生3非常著急的樣子，顯然有話要說(shuō)，于是示意生3也說(shuō)一說(shuō).

生3：老師先前講過(guò)“特殊化”的思想，在這里，如果我們先從特殊情況入手獲得定點(diǎn)T，再證明該點(diǎn)對(duì)一般情況也適合，是不是也可以得解.

師：從特殊到一般來(lái)研究問(wèn)題，快速找到突破點(diǎn)，這是很好的想法，大家不妨試一下.

數(shù)分鐘后：

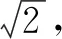
令y=0，可得x=1,或x=2.下面再檢驗(yàn)一下一般情況.

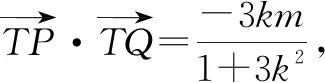
(2)若T(2,0)，此時(shí)……符合題意.

綜上所述，存在定點(diǎn)T(2,0)滿足|PQ|=2|NT|.

以上是筆者微設(shè)計(jì)的全部?jī)?nèi)容，但一路走下來(lái)，心里怪怪的，總有差那么一點(diǎn)的感覺(jué)，就在這時(shí)，生4同學(xué)舉手示意，“老師，我還有一種想法”.

生4：老師，我發(fā)現(xiàn)利用橢圓的切點(diǎn)弦方程，本題還可以這樣解.

師生不由得鼓起掌來(lái)，聽(tīng)到教室里面掌聲響起來(lái)，剛才那種“怪怪的感覺(jué)”也煙消云散了.

3 結(jié)束語(yǔ)

美國(guó)數(shù)學(xué)家波利亞在《怎樣解題》中說(shuō)過(guò),解題的價(jià)值不是答案的本身，而在于弄清“是怎樣想到這個(gè)解法的？”、“是什么促使你這樣想，這樣做的？”這就是深度學(xué)習(xí)的基本特征之一:要“學(xué)透”知識(shí)，不僅知其然也要知其所以然，還要知其可能然.深度學(xué)習(xí)的另一個(gè)基本特征就是要“學(xué)活”知識(shí)，要做到活學(xué)活用，舉一反三，并能夠依據(jù)不同情境創(chuàng)造性的遷移和應(yīng)用知識(shí)，靈活解決同一類型的不同問(wèn)題.以上兩個(gè)特征體現(xiàn)了深度學(xué)習(xí)“要關(guān)注知識(shí)、關(guān)注能力培養(yǎng)”，而深度學(xué)習(xí)的第三個(gè)基本特征則是要“參悟”知識(shí)，深度學(xué)習(xí)不止于文本，而是基于文本內(nèi)容的新的生長(zhǎng)和超越，這種生長(zhǎng)和超越，既可以是對(duì)文本內(nèi)容本身的拓展和深化，也可以是對(duì)文本內(nèi)容新的思考和體悟，這第三個(gè)基本特征則是要“見(jiàn)人”了，在“參悟知識(shí)”過(guò)程中提升核心素養(yǎng)、實(shí)現(xiàn)“立德樹(shù)人”的成長(zhǎng)，這就是“解題教學(xué)”彌足珍貴的價(jià)值.Z