一道全國高中聯賽向量題的探究及拓展
?貴州省湄潭縣湄江高級中學 楊 滔
1 引言
平面向量的最值問題一直是高考中非常常見的題型之一,可以涉及平面向量的模、夾角、數量積、參數值等多個要素,也是各類模擬卷、自主招生、競賽中比較常見的題型.平面向量的最值問題往往切入點多,方法多樣,而且難度一般都不低,是一個數學知識融合,創新意識應用,數學能力提升以及數學核心素養培養等的重要場所.
2賽題呈現
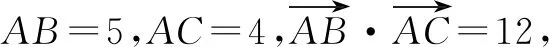
此題以三角形為載體,結合三角形的邊長與兩向量的數量積來確定已知的三角形,利用動點P的“動”態,結合數量積的“數”式,利用平面向量的線性運算與數量積運算來合理轉化,進而形成“形”式,確定“靜”態情況下相應的最值問題,創新性強,讓人眼前一亮.
3 問題破解
方法1:基本不等式法.
解析:取BC的中點D,連接AD.
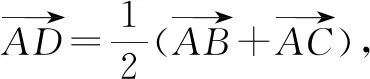


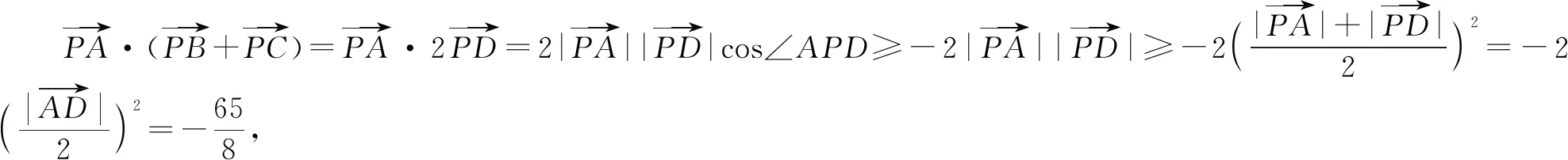
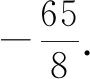

方法2:參數法.
解析:取BC的中點D,連接AD.
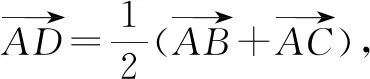


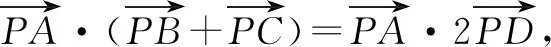

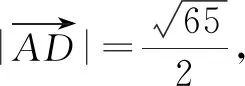
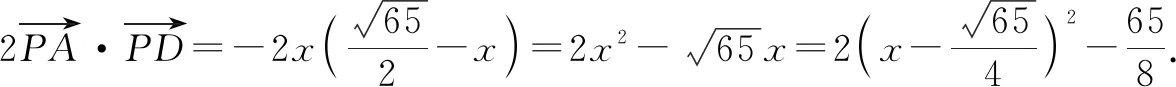
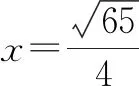
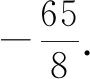

方法3:坐標法.
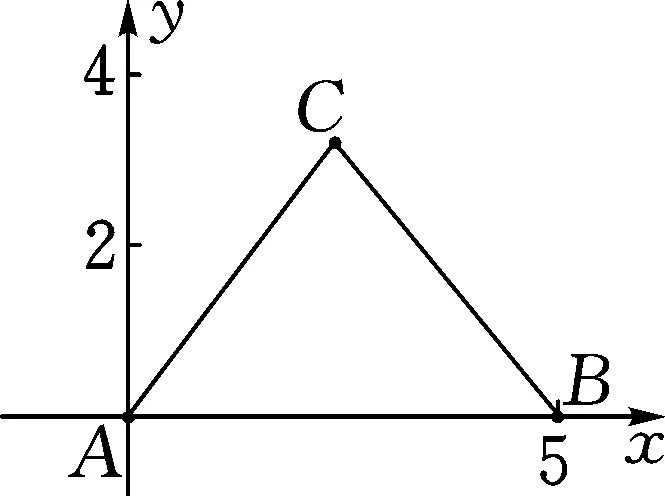
圖1
解析:以點A為坐標原點,AB所在的直線為x軸建立平面直角坐標系,如圖1所示.不失一般性,假定點C位于第一象限.
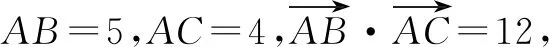
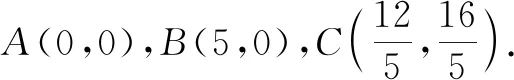
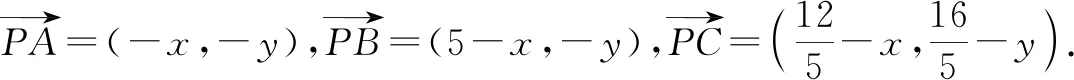
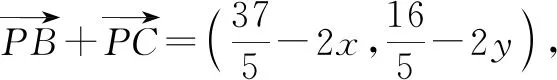
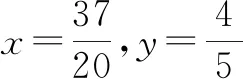
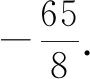
點評:以點A為坐標原點巧妙構造直角坐標系,結合題目條件確定點C的坐標,設出點P的坐標,利用平面向量的坐標運算與數量積公式得到涉及參數x,y的二次關系式,通過合理配方,結合函數思維來確定最值即可.坐標法可以借助平面直角坐標系的建立,以及坐標的代數運算來合理轉化,化“形”為“數”,利用代數運算來達到目的.
方法4:極化恒等式法.
解析:取BC的中點D,連接AD.
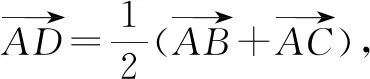


那么結合極化恒等式,可得
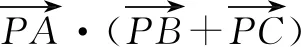

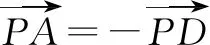
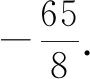

4 問題背景
以上賽題改編于2017年高考數學全國卷Ⅱ理科第12題,是在原來特殊三角形——等邊三角形的基礎上,加以一般化處理.
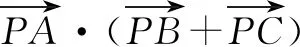
由于涉及特殊三角形——等邊三角形,此高考真題破解起來更為簡單快捷,可以參考以上賽題的破解方法加以分析與處理.(此題答案:B)
5 教學反思
5.1 方法歸納
在解決平面向量的數量積問題中,可以利用基底向量,借助平面向量的線性運算,結合基本不等式、極化恒等式等加以處理;也可以利用平面直角坐標系,借助平面向量的坐標運算,結合函數等加以處理;有時還可以直接利用圖形特殊,結合平面向量的“形”的特征加以處理;等等.這些都是競賽、高考中解決此類問題比較常見的一些技巧方法.
5.2 核心引領
在破解平面向量的最值問題時,問題切入的關鍵是根據題目條件,從平面向量的相關概念、相關運算、相關圖形的本質出發,選取代數與幾何、數與形等方式,以概念法、函數法、三角函數法、數形結合法以及不等式法等行之有效的基本方法來參與,借助平面向量的相關運算等來解決,進而有效達到解決相關最值問題的目的,融合數學知識,提升解題能力,拓展數學思維,培養核心素養.Z

