妙解排列組合里的涂色問題
?江蘇省江安高級(jí)中學(xué) 肖雄偉
1 一分步,二分類
對(duì)于某些不復(fù)雜的涂色問題,使用分步計(jì)數(shù)原理處理會(huì)更加簡(jiǎn)便.如果題目所給的條件比較多的時(shí)候,此時(shí)就應(yīng)該以題目的已知條件為依據(jù),把分步計(jì)數(shù)原理和分類計(jì)數(shù)原理結(jié)合起來進(jìn)行求解.在實(shí)際情況中,要牢記優(yōu)先處理有特殊要求的色塊.解題步驟為首先處理特殊的色塊,再依據(jù)實(shí)際情況,如果附加要求多,那就先使用分步計(jì)數(shù)原理,再使用分類計(jì)數(shù)原理解答;如果是不難的涂色問題,就可以直接運(yùn)用分步計(jì)數(shù)原理解題.
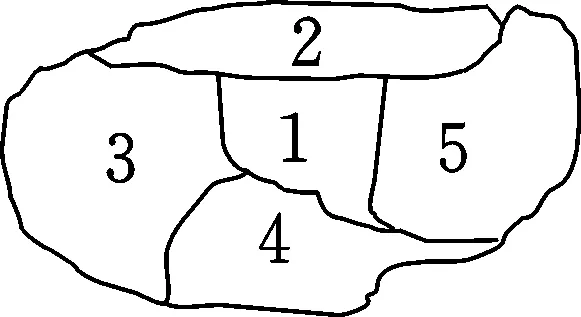
圖1
例題1假設(shè)中國(guó)的某一個(gè)省由5個(gè)市區(qū)組成,這個(gè)省的市區(qū)分布如圖1所示,現(xiàn)給地圖上色,要求相鄰區(qū)域使用的顏色不能相同,現(xiàn)有4種顏色可供選擇,那么不同的上色方法一共有種.
分析:這個(gè)題目與很多題目都有相似的地方,但是圖形是有變化的,因此就需要學(xué)生有較強(qiáng)的觀察能力和分析能力.分析發(fā)現(xiàn),市區(qū)1與其他市區(qū)不一樣,它跟另外的四個(gè)市區(qū)都是相鄰的,被其他四個(gè)市區(qū)包圍著.因此在解答題目的時(shí)候,需要優(yōu)先考慮分步計(jì)數(shù)的方法,即首先將市區(qū)1涂上顏色,那么市區(qū)1就有4種選擇方法,再利用分類計(jì)數(shù)的方法,當(dāng)市區(qū)2和市區(qū)4的顏色一樣的時(shí)候,就有3種上色方法,那么總的上色方法就有4×3×2×2=48種;當(dāng)市區(qū)2和市區(qū)4的顏色不一樣的時(shí)候,優(yōu)先給市區(qū)2上色的方法有3種,此時(shí)市區(qū)4就有兩種上色方法,那么市區(qū)3和市區(qū)5就只有一種上色方法,因此此時(shí)上色的總方法數(shù)為:4×3×2×1×1=24種.所以,一共有24+48=72種上色方法.

圖2
推廣1如圖2,用4種不同顏色給圖中A,B,C,D,E,F(xiàn)六個(gè)點(diǎn)涂色,要求每個(gè)點(diǎn)都要涂一種顏色,且圖中每條線段的兩個(gè)端點(diǎn)涂不同的顏色,則不同的涂色方法有種.
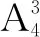
2 一分類,二分步
對(duì)于某些較為復(fù)雜繁瑣的涂色問題,就需要首先以使用顏色的種類為依據(jù)進(jìn)行分類,特別是不同的題目對(duì)于要求使用顏色的種類也不一樣.當(dāng)題目中出現(xiàn)要求三種顏色時(shí)就需要進(jìn)行分類計(jì)數(shù),如果沒有出現(xiàn)最多使用三種顏色的要求,那么問題就更復(fù)雜了,還需要做深入的思考和處理,分類計(jì)數(shù)原理是處理此類復(fù)雜問題的首要方法.即解題步驟為首先分析題目要求的用色的種類,要求有最多使用三種顏色的就可以進(jìn)行分類,如果沒有最多三種顏色這個(gè)條件的要求,那么需要再思索.一般來說,中學(xué)階段出現(xiàn)后面這種情況的題型很少.

圖3
例題2
.
.
分析:分析題目信息可以知道,此題與例題1有共同的特點(diǎn),就是結(jié)合使用分步和分類的方法來解題,但它明顯比例題1復(fù)雜得多.因此對(duì)于此題應(yīng)該首先以使用顏色的種類為依據(jù)來進(jìn)行分類,這樣就會(huì)簡(jiǎn)便許多,出錯(cuò)的幾率也會(huì)相應(yīng)減小.分類方式有兩種:
因此,一共有30+360=390種上色方法.
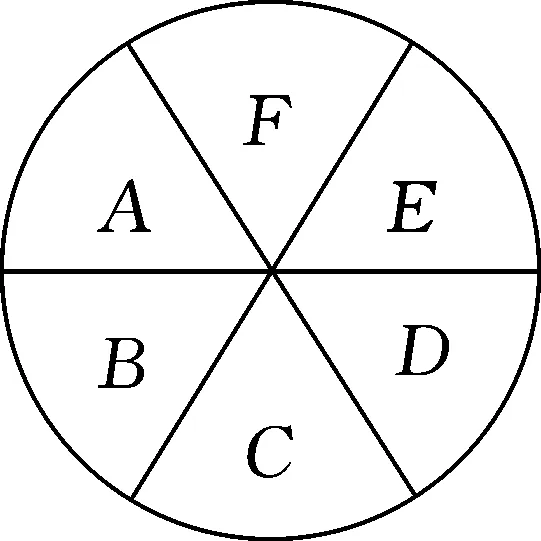
圖4
推廣2在一個(gè)正六邊形的六個(gè)區(qū)域內(nèi)栽種觀賞植物,如圖4,要求同一塊區(qū)域內(nèi)栽種同一種植物,相鄰的兩塊區(qū)域種植不同的植物,現(xiàn)有4種不同的植物可供選擇,則有種種植方案.
分析:對(duì)問題所給條件分析,不難發(fā)現(xiàn)解答該問題需要使用分類計(jì)數(shù)原理和分步計(jì)數(shù)原理.以種植植物的種類個(gè)數(shù)為依據(jù)計(jì)算,進(jìn)而求解具體種植方案仍具有一定難度.應(yīng)考慮局部分類法,即以不相鄰區(qū)域的種植植物種類個(gè)數(shù)為分類依據(jù),進(jìn)一步計(jì)算種植方案.則該問題可以分為三類情況:


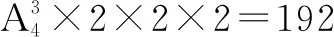
所以,一共有種植方案108+432+192=732種.
在此,通過以上對(duì)范式理論和集約相關(guān)理論的研究探討,可將維修集約范式初步界定為:在資源優(yōu)化配置和有效使用的原則下,通過綜合組織、設(shè)計(jì)維修主體和維修程式,而形成的緊湊、高效、有序的維修活動(dòng)組織及可持續(xù)發(fā)展模式。維修集約范式的內(nèi)涵組成如圖1所示。其中,維修主體是實(shí)施、管理和評(píng)價(jià)維修活動(dòng)的作業(yè)單位;將維修主體開展的維修業(yè)務(wù)流程定義為維修程式,即將基于一定的維修資源,運(yùn)用一定的維修策略,在一定的維修作業(yè)地點(diǎn),對(duì)一定的維修對(duì)象開展的一系列維修活動(dòng)。
3 一平面,二空間
對(duì)于一些很難掌握的點(diǎn)線面需要涂色的立體圖形,由于相鄰的地方比較多,因此就需要先把立體問題轉(zhuǎn)化成為平面上的問題,然后再以使用顏色的種類為依據(jù)進(jìn)行分類解答.即解題步驟為首先將立體圖形轉(zhuǎn)化成為平面圖形,再根據(jù)題目情況分類,具體的分類情況由實(shí)際題目的要求決定,分類依據(jù)還是以使用的顏色種類為依據(jù),分別進(jìn)行討論求解,最后所有情況相加就是需要求的總的情況數(shù).
例題3已知有一個(gè)四棱錐P-ABCD,如圖5所示,使用4種不同的顏色在四棱錐的每個(gè)面上上色,要求相鄰的區(qū)域顏色不同,一共有多少種涂法?
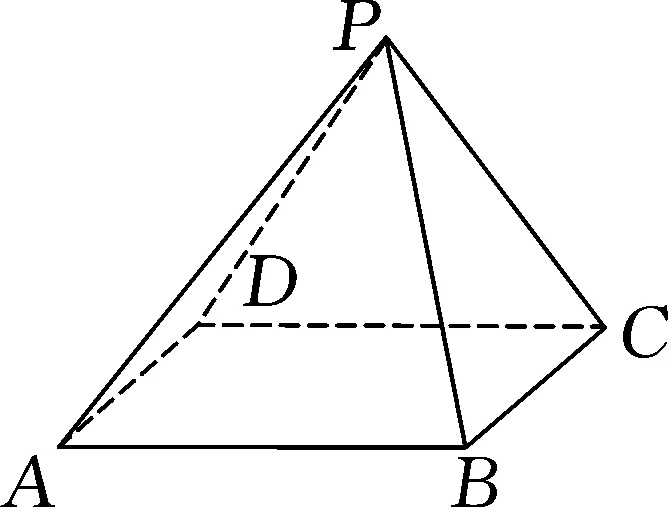
圖5

圖6
分析:分析可知,此題需要將立體圖形轉(zhuǎn)化成平面圖形,在平面區(qū)域中涂色.如圖6所示,區(qū)域1,2,3,4等價(jià)于四棱錐的側(cè)面,區(qū)域5等價(jià)于底面.下面就以使用的顏色的種類來分類:
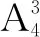
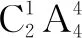
推廣3用6種不同顏色給三棱柱ABC-DEF的面涂色,如圖7所示,要求有公共棱的平面涂色不相同,則有多少種涂色方法?
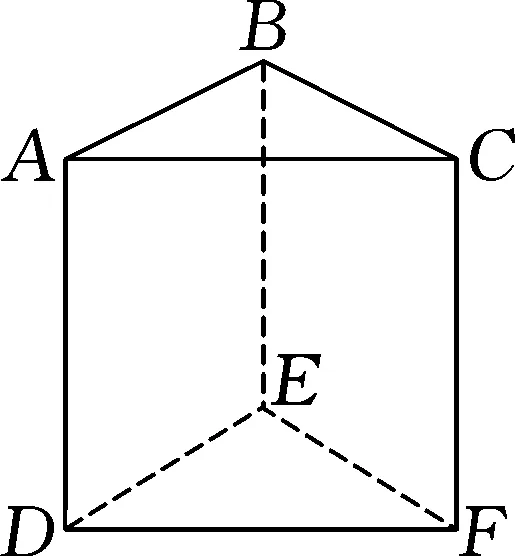
圖7
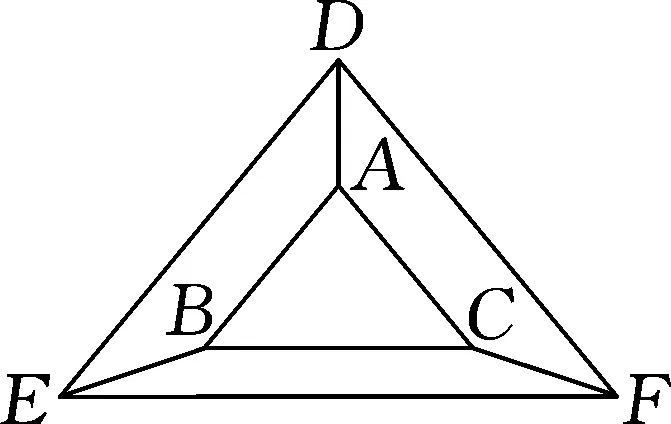
圖8
分析:根據(jù)例題3可知,幾何體有關(guān)于平面的涂色問題,解答時(shí)通常轉(zhuǎn)化為平面圖形進(jìn)行求解.則該問題的求解思路與之類似,即將圖7的三棱柱ABC-DEF轉(zhuǎn)變?yōu)閳D8的平面圖形,以涂色顏色的種類為依據(jù)分類進(jìn)行求解,其中圖7中三棱柱的底面DEF也需要涂色.由已知條件可知,至少需要上4種顏色,具體的解題過程為:
涂色方法計(jì)數(shù)問題是目前排列組合問題的重難點(diǎn),要學(xué)會(huì)正確的解答思路.解決此類問題的策略,首先要分析題目,然后再根據(jù)題目選擇合適的解題方法,正確使用分類和分步計(jì)數(shù)原理.對(duì)于排列組合的基礎(chǔ)知識(shí)也需要掌握牢固,避免出現(xiàn)基礎(chǔ)性的錯(cuò)誤.

