高中數學“一題多解”教學的實踐
?張家港高級中學 劉 學
1 引言
在高中數學解題教學中,為進一步培養學生的解題技巧與解題水平,教師通常會專門設計一些“一題多解”類的專題訓練,鼓勵他們面對同一道題目時盡量找出更多不同解法.這一模式能激活學生的自主思維,使其全身心地投入到思考中,有助于他們更好地鞏固數學知識與技能.
2 一題多解在教學中的應用
2.1 集合問題的中一題多解
集合是高中數學教材中第一章節的內容,也是高中數學知識體系中的基礎構成部分,是學生學習函數知識的前提,雖然題目難度一般,但是也有不少一題多解類試題,教師可以利用這類題目,讓學生嘗試運用多種方法解決問題,讓他們進一步了解集合的含義,體會元素和集合的“屬于”關系,為利用集合的思想方法解決簡單實際問題做鋪墊.
例1已知集合M={x|y2=x+1},P={x|y2=-2(x-3)},那么M∩P=( ).
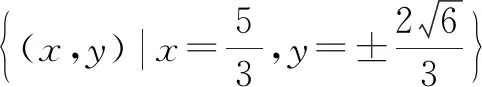
C.[-1,3] D.(-∞,3)
解析:能識別出集合M與P的元素的特征,是求得M和P交集的關鍵所在.M∩P的元素并非(x,y),而是x的形式.
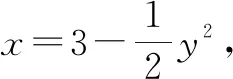
解法2:使用排除法,因為M∩P的元素均是x,并非簡單(x,y)的形式,將A排除掉;比較B,C兩項,假如取x=-1,-1∈M,-1∈P,得知-1∈(M∩P),排除B;再比較C與D,取x=-2,-2?M,D也排除.正確答案為:C.
針對上述案例,學生采用不一樣的解題方法處理這一題目,使其理清集合的本質,明確元素的特點具有互異性,再通過代入檢驗求出兩個集合的交集,讓他們學會處理該類試題.
2.2 函數問題中的一題多解
函數作為學生從初中階段就開始接觸到的一類知識,步入高中階段以后,函數的知識范圍有所擴大,更是出現不少新型函數,而且對函數的研究更為深入,是學生的學習重點與難點.在高中數學函數解題訓練中,教師同樣可以利用一題多解類的試題,引領學生從多個角度看待問題,促使他們充分運用所學知識與已知條件通過合理正確的方式來解題.
例2在銳角三角形ABC中,如果sinA=2sinBsinC,那么tanAtanBtanC的最小值是多少?
這是一道典型的三角函數類題目,學生分析、討論后能夠找到以下幾種解法.
解法1:根據題意可得
①
令 cosBcosC=tcosA
②
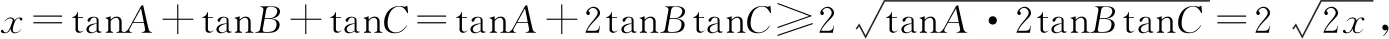
上述案例,從兩種完全不同的解題方法來看運用的是兩種思路,用到的數學知識也不一樣,這樣能夠拓展學生的思維空間,使其嘗試從多個層面與角度解題,讓他們學會舉一反三.
2.3 數列問題中的一題多解
在高中數學課程教學中,數列也是一類較為重要的內容,包括等差數列與等比數列兩大類,在高考中出現的頻率較高,是熱門考點之一.高中數學教師在數列解題教學中,應當巧妙設置一些一題多解的題目,引導學生靈活運用數列的相關知識展開分析與探討,有效拓展解題思維空間,使其尋找到最優解題思路與方法,繼而提高他們的解題速度與準確度.
例3在等差數列{an}中,a1<0,S9=S12,那么數列{an}的前幾項和最小?
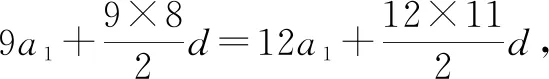
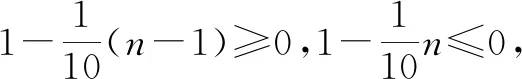
解法2:根據S9=S12可知a10+a11+a12=3a11=0,則a11=0,又因為a1<0,所以公差d>0,據此能夠判斷出數列{an}前10項或前11項的和最小.
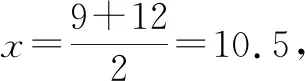
如此,學生分別按照常規思路分析,根據等差數列的概念公式,通過尋找轉折項運用等差中項的性質,或采用函數思想將數列問題轉化成函數問題的方式解題,使其思路更為靈活.
2.4 不等式問題的一題多解
雖然學生從小學階段就有所接觸不等式,像簡單的大于、小于、大于等于、小于等于等算式和數量關系,不過高中階段的不等式知識更為深奧,涉及到的題目難度也更大,對他們的知識水平與解題能力要求較高.所以,高中數學教師可以在不等式問題中設置一題多解訓練,引領學生充分運用所學知識通過多種解題方法來處理問題,增強他們的解題自信心.

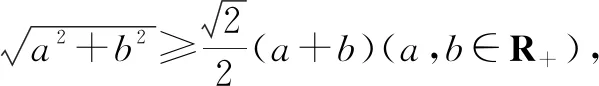
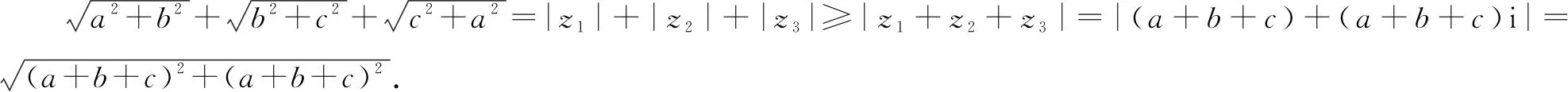
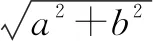
對于上述案例,這三種證明方法跨度大,分別利用基本不等式的性質、復數模的性質及數形結合思想,學生通過尋找更多解題方法,可有效活化他們的數學思維,改善解題水平.
2.5 幾何問題中的一題多解
數學主要由代數與幾何兩大部分構成,高中數學課程體系中的幾何知識以立體幾何與解析幾何為主,對學生的抽象思維能力、幾何直觀能力與空間想象力有著較高要求,他們在解題中極易遇到障礙.高中數學教師在解題教學環節,可以針對幾何問題精心設計一些題目,要求學生運用多種不一樣的解題方法,使其掌握更多處理幾何問題的技巧,提高解題效率.
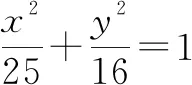
A.有兩個點PB.有四個點P
C.可能不存在點PD.一定不存在點P
解法1:把線段F1F2當作直徑畫一個圓,已知圓的半徑r=c=3<4=b,所以圓和橢圓不會相交,即不存在點P.
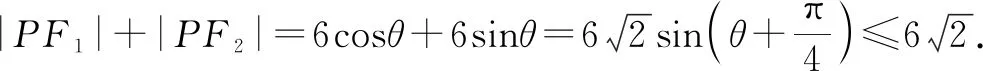
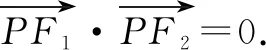
在上述案例中,面對這樣一道難度一般的解析幾何類題目,學生可以輕松找到多個不一樣的解題方法,使其充分體會到一題多解的樂趣,同時讓他們通過比較發現最優解題思路.
3 結語
總而言之,高中數學具有較強的理論性與學科性特征,在學習與解題訓練中經常會遇到不少挑戰,教師應用“一題多解”的訓練模式,可以有效活化學生的思維,使其拓展解題思路,掌握高效的解題方法,慢慢增強他們的解題自信.Z

