函數與導數中的不等式問題

■廣東省佛山市順德區容山中學 潘敬貞

函數與導數中的不等式問題一直是高考考查的熱點和難點問題,主要包括兩種類型:已知不等式求參數的范圍和證明不等式。該類問題的求解對同學們的分析問題、轉化與化歸、代數變形、構造新函數、分類討論、推理論證、運算求解等能力要求比較高。本文結合實例對常見的函數與導數中的不等式問題進行歸納、梳理,主要目的是加強同學們對該類題備考的針對性,提高解決該類問題的能力,從而提高高考競爭力。

一、已知不等式求參數的范圍

例1已知函數f(x)=(x-1)exa(x2+1),x∈[1,+∞)。

(1)討論函數f(x)的單調性;

(2)若f(x)≥-2a+lnx,求實數a的取值范圍。

解析:(1)略。

(2)令g(x)=f(x)+2a-lnx=(x-1)ex-a(x2-1)-lnx,注意到g(1)=0,則問題轉化為g(x)≥0在x∈[1,+∞)上恒成立。

g＇(x)=xex-2ax-。

若a＞,則g＇(1)=e-2a-1＜0;g＇(ln(2a+1))=ln(2a+1)-,因為2a+1＞e,所以ln(2a+1)＞1,g＇(ln(2a+1))＞0。所以存在x0∈(1,ln(2a+1)),使得g＇(x0)=0。

當x∈(1,x0)時,g＇(x)＜0,g(x)單調遞減,所以g(x)＜g(1)=0,不滿足題意。

若a≤,則g＇(x)≥xex-(e-1)x=x[ex-(e-1)]-。

當x＞1時,x[ex-(e-1)]＞1,0＜＜1,所以g＇(x)＞0,g(x)在[1,+∞)上單調遞增,所以g(x)≥g(1)=0,滿足題意。

綜上可得,a≤。

評注:解答本題的關鍵是由g＇(1)=0得a=,后面只需討論a＞和a≤時函數g(x)的符號即可。

例2已知函數f(x)=aex-2ax-2(a≠0)。

(1)討論函數f(x)的單調性;

(2)是否存在a∈(0,1),使得對于任意實數x,都有f(x)+＞0?

解析:(1)f＇(x)=aex-2a=a(ex-2),令f＇(x)=0,得x=ln 2。

若a＞0,當x∈(-∞,ln 2)時,f＇(x)＜0,函數f(x)單調遞減;當x∈(ln 2,+∞)時,f＇(x)＞0,函數f(x)單調遞增。

若a＜0,當x∈(-∞,ln 2)時,f＇(x)＞0,函數f(x)單調遞增;當x∈(ln 2,+∞)時,f＇(x)＜0,函數f(x)單調遞減。

(2)方法1:f(x)+=aex-2ax-2+＞0,可變形為ae2x-(2ax+2)·ex+(x2+2x)＞0。

令g(x)=ae2x-(2ax+2)ex+(x2+2x),則g＇(x)=2ae2x-(2ax+2a+2)ex+(2x+2)=2(aex-1)(ex-x-1)。

令h(x)=ex-x-1,則h＇(x)=ex-1,由h＇(x)=0,得x=0。

當x∈(-∞,0)時,h＇(x)＜0,函數h(x)單調遞減;當x∈(0,+∞)時,h＇(x)＞0,函數h(x)單調遞增。

因此,不存在a∈(0,1),使得對于任意實數x,都有f(x)+＞0。

由(1)知,當a＞0時,f(x)min=f(ln 2)=2a-2aln 2-2。

g＇(x)=,令g＇(x)=0,得x=。

所以g(x)在(-∞,)上單調遞增,在上單調遞減,在上單調遞增。

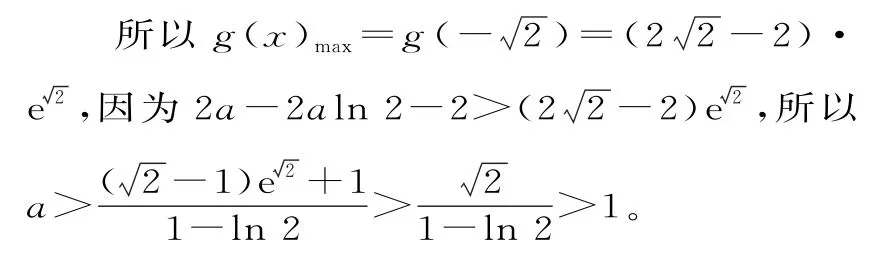
因此,不存在a∈(0,1),使得對于任意實數x,都有f(x)+＞0。

方法3:假設存在a∈(0,1),使得對于任意實數x,都有f(x)+＞0,即aex-2ax-2+＞0。令h(x)=ex-2x,則h＇(x)=ex-2。當x∈(-∞,ln 2)時,h＇(x)＜0,h(x)單調遞減;當x∈(ln 2,+∞)時,h＇(x)＞0,h(x)單調遞增。所以h(x)min=h(ln 2)=2-2ln 2＞0,所以ex-2x＞0,所以a＞恒成立。

令F(x)=,則F＇(x)=。

令Q(x)=ex-x-1,則Q＇(x)=ex-1。當x∈(-∞,0)時,Q＇(x)＜0,Q(x)單調遞減;當x∈(0,+∞)時,Q＇(x)＞0,Q(x)單調遞增。所以Q(x)≥Q(0)=0,所以ex≥x+1。

而獲得了知識和美德的人，就可以出色地運用其天生就具備的武器(即各種能力)，而美德一旦武裝起來就能形成極強的能力；如果人們的品德敗壞了，比如極其邪惡和殘暴，無比放蕩和貪婪，就會把我們天生的武器用于做極惡劣的事情。“不公正被武裝起來將會是莫大的禍害。”[2](P7)善德與惡德對于個人和團體的生活之影響十分巨大，所以，政治的作用就是要采取優良政體，或者促使時下的各種政體能夠得到改善，其標準就是：有效地安排各種善，并使美德的價值優先；同時政體的安排要有助于公民獲得美德，并且可以按照政體能在多大程度培養公民的完整美德來衡量其優良程度。

令g(x)=x2-ex,則g＇(x)=2x-ex＜0,所以g(x)在R 上單調遞減。

又g(-1)=1-＞0,g(0)=-1＜0,所以?x0∈(-1,0),使得g(x0)=0,從而F＇(x0)=0,此時。

當x∈(-∞,x0)時,F＇(x)＞0,F(x)單調遞增;當x∈(x0,+∞)時,F＇(x)≤0,F(x)單調遞減。所以F(x)max=F(x0)=＞1,所以a＞1,矛盾。

因此,不存在a∈(0,1),使得對于任意實數x,都有f(x)+＞0。

評注:本題是以探究存在性問題進行設問,具有濃厚的探究味道,但本質上和已知不等式求參數范圍是一致的,本題的方法1 是正面突破,將問題轉化為求函數的最值問題,通過一系列推導和求解得出矛盾,最后下結論,這是這類問題的一般解法,但過程有點煩瑣;方法2 是將問題轉化為f(x)min＞g(x)max,從而求得實數a的取值范圍,最后得出結論,該思路也非常清晰、自然,解答過程簡潔,是一種好的解法;方法3是通過分離參數,然后構造新函數,該解法容易理解,也常用,但對運算能力要求比較高,解答過程比較繁雜,沒有一定的數學功底很難完整地解答出來。

二、證明函數不等式

有關證明不等式問題,一般有轉化后求函數的最值問題,極值點偏移問題,對數均值不等式問題,有時還需要對函數進行同構等。

例3已知函數f(x)=x2+ax+2lnx(a為常數)。

(1)當a≤4 時,討論函數f(x)的單調性;

(2)若f(x)存在兩個極值點x1,x2,且|x1-x2|≤,證明:|f(x1)-f(x2)|≤-4ln 2。

解析:(1)函數f(x)的定義域為(0,+∞)。

f＇(x)=2x+a+。

設g(x)=2x2+ax+2(x＞0)。

當-4≤a≤4時,Δ≤0,2x2+ax+2≥0成立,則f＇(x)＞0,所以函數f(x)在(0,+∞)上單調遞增。

(2)由(1)知函數f(x)的兩個極值點x1,x2滿足2x2+ax+2=0,所以x1x2=1,x1+x2=。

不妨設0＜x1＜1＜x2,則f(x)在(x1,x2)上是減函數,故f(x1)＞f(x2)。

評注:本題第(2)問根據題意利用韋達定理將參數消掉,進而將問題轉化為求函數的最值問題,解題過程中的換元、變形是關鍵,試題難度較大,需要豐富的解題經驗和較高的數學綜合能力。

函數不等式問題一直是高考考查的熱點問題,也是難點問題,一般都是考卷中的壓軸題,該類題的解決對同學們的數學能力要求較高,不僅需要豐富的解題經驗,還需要很強的推理論證和運算求解能力。只有勤于思考,經常歸納解題思路,提煉思想方法,不斷反思小結,從而提高自己的數學綜合能力,才能在高考考場中擊敗函數與導數壓軸題。