函數與導數的綜合應用試題精選

■安徽省利辛高級中學 胡彬

■安徽省利辛縣中疃鎮中心校 張建國

1.已知函數f(x)=x-mlnx-(m∈R),g(x)=+ex-xex。

(1)若m＜e+1,試求f(x)在[1,e]上的最小值;

(2)當m≤2 時,若存在x1∈[e,e2],使得對任意的x2∈[-2,0],都有f(x1)≤g(x2)成立,求實數m的取值范圍。

2.已知函數f(x)=lnx-ax2+(2-a)·x(a∈R)。

(1)討論f(x)的單調性;

(2)若對任意的x∈(0,+∞),都有f(x)+a(x2+x-xex)≤x-1成立,求實數a的取值范圍。

3.已知函數f(x)=xex-ax-alnx+a。

(1)若a=e,判斷函數f(x)的單調性,并求出函數f(x)的最值;

(2)若函數f(x)有兩個零點,求實數a的取值范圍。

4.已知函數f(x)=。

(1)求f(x)的極值。

(2)若a＞0,且a≠1,函數y=f(x)-f(a)有且僅有兩個零點,求a的取值范圍。

5.已知函數f(x)=(x-m)lnx在x=e處的切線與直線2x-y+2=0平行。

(1)求m的值,并求此切線方程;

(2)證明:f(x)＜ex+cosx-1。

6.已知函數f(x)=alnx+x2-(a+2)x,其中a為常數,且a≠0。

(1)當a＞0時,若f(x)在(0,e]上的最大值為1,求實數a的值;

(2)若a＜0,且函數f(x)有兩個不相等的零點x1,x2,證明:x1+x2＞2。

7.已知函數f(x)=ax2-(a+2)x+lnx(a＞0)。

(1)討論函數f(x)的單調性;

(2)若存在x∈[1,+∞),使得f(x)+e≤0成立,求實數a的取值范圍。

8.已知函數f(x)=ax-(2a+1)lnx-。

(1)討論函數f(x)的單調性;

(2)若?a∈[2,3],?x1,x2∈[1,2],不等式m+ln 2＞|f(x1)-f(x2)|恒成立,求實數m的取值范圍。

9.已知函數f(x)=lnx-aex(a∈R)。

(1)若f(1)=1,求曲線y=f(x)在點(1,1)處的切線方程;

(2)當a＞0時,若對任意的x＞0,都有f(x)≤lna成立,求a的取值范圍。

10.已知函數f(x)=。

(1)討論f(x)的單調性,并比較20212022與20222021的大小;

(2)若a,b為兩個不相等的正數,且alna=blnb,求證:a+b＞2e·ab。

11.設函數f(x)=x2-axlnx,a∈R。

(1)若a=1,求曲線y=f(x)在點(1,f(1))處的切線方程。

(2)若存在x0∈[1,e],使得f(x0)＜-e(a+e)成立,求a的取值范圍。

12.已知函數f(x)=ax--2lnx(a＞0,b＞0)。

(1)若f(x)在定義域上單調遞增,求ab的最小值;

(2)當a=1,b＞1時,f＇(x)=m有兩個不同的實數根x1,x2,證明:f(x1)+f(x2)+2m＞0。

13.已知函數f(x)=2lnx+x2+(a-1)·x-a(a∈R),當x≥1時,f(x)≥0恒成立。

(1)求實數a的取值范圍;

(2)若正實數x1,x2(x1≠x2)滿足f(x1)+f(x2)=0,證明:x1+x2＞2。

參考答案:

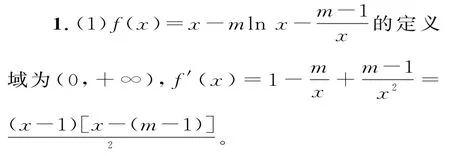
若m≤2,當x∈[1,e]時,f＇(x)≥0,所以f(x)在[1,e]上是增函數,則f(x)min=f(1)=2-m。

若2＜m＜e+1,當x∈[1,m-1]時,f＇(x)≤0;當x∈[m-1,e]時,f＇(x)≥0。所以f(x)min=f(m-1)=m-2-mln (m-1)。

(2)已知條件等價于f(x1)min≤g(x2)min。

由(1)知,當m≤2 時,在x1∈[e,e2]上有f＇(x1)≥0,所以f(x)為單調遞增函數,所以f(x1)min=f(e)=e-m-。

又g＇(x)=x+ex-(x+1)ex=x(1-ex),當x2∈[-2,0]時,g＇(x2)≤0,所以g(x2)min=g(0)=1。

所以m≤2 且e-m-≤1,解得≤m≤2。

所以實數m的取值范圍為。

2.(1)函數f(x)的定義域為(0,+∞),f＇(x)=-2ax+2-a=。

當a≤0 時,f＇(x)＞0 恒成立,所以f(x)為遞增函數。

當a＞0時,令f＇(x)＞0,得0＜x＜;令f＇(x)＜0,得x＞。所以f(x)在上為遞增函數,在上為遞減函數。

綜上可得,當a≤0 時,f(x)為遞增函數;當a＞0 時,f(x)在上為遞增函數,在上為遞減函數。

(2)由題意得,對任意的x∈(0,+∞),都有f(x)+a(x2+x-xex)≤x-1 成立,即a≥恒成立。

令g(x)=,則g＇(x)=。

令h(x)=x+lnx,則h＇(x)=1+,所以h(x)在(0,+∞)上單調遞增。

當x∈(0,x0)時,h(x)＜0,g＇(x)＞0,g(x)單調遞增;

當x∈(x0,+∞)時,h(x)＞0,g＇(x)＜0,g(x)單調遞減。

所以g(x)max=g(x0)=。

由x0+lnx0=0,得x0=-lnx0,則,所以g(x)max=g(x0)==1。

又a≥恒成立,所以a≥1。

綜上可得,實數a的取值范圍為[1,+∞)。

3.(1)函數f(x)的定義域為(0,+∞),當a=e時,f(x)=xex-ex-elnx+e,所以f＇(x)=(x+1)ex-e-=(x+1)·。

當x∈(0,1)時,f＇(x)＜0;

當x∈(1,+∞),f＇(x)＞0。

所以f(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增。

所以f(x)的最小值為f(1)=e-eeln 1+e=e,無最大值。

(2)由(1)知f＇(x)=。

當a≤0時,f＇(x)＞0 在(0,+∞)上恒成立,所以f(x)在(0,+∞)上單調遞增,故函數f(x)在(0,+∞)上至多有一個零點,不符合題意。

當a＞0時,令ex-=0,設該方程的解為x0,則在(0,x0)上,f＇(x)＜0;在(x0,+∞)上,f＇(x)＞0。所以f(x)在(0,x0)上單調遞減,在(x0,+∞)上單調遞增。

為了滿足f(x)有兩個零點,則有f(x0)=-ax0-alnx0+a＜0。 ①

又x0是方程ex-=0的解,則=a,兩邊取對數得lnx0+x0=lna。 ②

將②式代入①式可得f(x0)=a(2-lna)＜0,所以a的取值范圍為(e2,+∞)。

當a∈(e2,+∞)時,由②式得x0＞1,f(1)=e-a+a=e＞0,所以f(x)在(0,x0)上僅有1 個零點;當x→+∞時,f(x)→+∞,故f(x)在(x0,+∞)上僅有1個零點。

綜上可得,若函數f(x)存在兩個零點,則實數a的取值范圍為(e2,+∞)。

4.(1)由題設得f＇(x)=。

當x∈(0,e)時,f＇(x)＞0,f(x)遞增;

當x∈(e,+∞)時,f＇(x)＜0,f(x)遞減。

所以f(x)的極大值為f(e)=,無極小值。

(2)要使y=f(x)-f(a)有且僅有兩個零點,則f(x)與y=有兩個交點。

由(1)可得,當x∈(0,e)時,f(x)∈;當x∈(e,+∞)時,f(x)∈。

又a＞0,且a≠1,所以當a∈(1,e),(e,+∞)時,f(a)∈。

所以a的取值范圍為(1,e)∪(e,+∞)。

5.(1)因為f＇(x)=lnx+1-,所以f＇(e)=2-。

因為f(x)在x=e處的切線與直線2xy+2=0平行,所以切線的斜率為2。

所以f＇(e)=2-=2,解得m=0。

所以f(x)=xlnx,所以f(e)=e。

故所求切線方程為y-e=2(x-e),即2x-y-e=0。

(2)要證f(x)＜ex+cosx-1,即證xlnx＜ex+cosx-1。

①當x∈(0,1]時,xlnx≤0,所以ex-1＞0,cosx＞0,所以ex+cosx-1＞0,所以xlnx＜ex+cosx-1。

②當x∈(1,+∞)時,令g(x)=ex+cosx-1-xlnx,則g＇(x)=ex-sinxlnx-1,g″(x)=ex-cosx-。

當x＞1 時,ex＞e,-1≤cosx≤1,0＜＜1,所以ex-cosx-＞0,即g″(x)＞0。

所以g＇(x)在(1,+∞)上單調遞增,所以g＇(x)＞g＇(1)=e-sin 1-1＞0。

所以g(x)在(1,+∞)上單調遞增,所以g(x)＞g(1)=e+cos 1-1＞0,即xlnx＜ex+cosx-1在(1,+∞)上恒成立。

綜上可得,f(x)＜ex+cosx-1。

6.(1)函數f(x)=alnx+x2-(a+2)x的定義域為(0,+∞),f＇(x)=+2x-(a+2)=。

綜上可得,實數a的值為。

(2)由(1)知f＇(x)=。

令f＇(x)=0,得x1=1,x2=。

當a＜0時,函數f(x)在(0,1]上單調遞減,在(1,+∞)上單調遞增。

因為函數f(x)有兩個不相等的零點x1,x2,不妨設x1＜x2,則x1∈(0,1),x2∈(1,+∞)。

構造函數g(x)=f(x)-f(2-x),x∈(0,1),則g(1)=0,g(x)=alnx+x2-(a+2)x-[aln(2-x)+(2-x)2-(a+2)(2-x)]=a[lnx-ln(2-x)-2x+2],則g＇(x)=＜0,所以g(x)在(0,1)上單調遞減,g(x)＞g(1)=0,所以當x∈(0,1)時,f(x)＞f(2-x)恒成立。

因為x1∈(0,1),所以f(x1)＞f(2-x1)恒成立,即f(x1)=f(x2)＞f(2-x1)。

因為x2,2-x1∈(1,+∞),且函數f(x)在(1,+∞)上單調遞增,所以x2＞2-x1,所以x1+x2＞2。

7.(1)函數f(x)=ax2-(a+2)x+lnx的定義域為(0,+∞),f＇(x)=2ax-(a+2)+。

(2)若存在x∈[1,+∞),使得f(x)+e≤0成立,即f(x)min≤-e成立。

由(1)可知,當a≥1 時,f(x)在[1,+∞)上單調遞增,所以f(x)min=f(1)=-2,不滿足f(x)min≤-e。

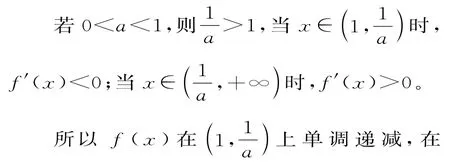
8.(1)函數f(x)的定義域為(0,+∞),,

令f＇(x)=0,得x=2或x=。

由(1)知,當x∈[1,2]時,f＇(x)＜0,所以函數f(x)在[1,2]上單調遞減,則f(x)max=f(1)=a-2,f(x)min=f(2)=2a-1-(2a+1)ln 2。

因為?x1,x2∈[1,2],不等式m+ln 2＞|f(x1)-f(x2)|恒成立,所以m+ln 2＞f(x)max-f(x)min=a-2-[2a-1-(2a+1)ln 2]=(2ln 2-1)a+ln 2-1,即m＞(2ln 2-1)a-1?a∈[2,3]恒成立。

令φ(a)=(2ln 2-1)a-1,則函數φ(a)在[2,3]上單調遞增,所以m＞φ(a)max=φ(3)=6ln 2-4。

所以實數m的取值范圍為(6ln 2-4,+∞)。

9.(1)因為f(x)=lnx-aex(a∈R),所以f(1)=-ae=1,即a=,所以f(x)=lnx+。

所以f＇(x)=·ex,f＇(1)=2,所以切線方程為y=2x-1,即2x-y-1=0。

(2)當a＞0且x＞0時,f(x)≤lna恒成立,即aex-lnx+lna≥0恒成立。

設h(x)=aex-lnx+lna,x＞0,則h＇(x)=aex-在(0,+∞)上是增函數。

作出函數y=aex與y=的大致圖像,如圖1 所示,可知函數y=aex與y=有一個交點,即h＇(x)在(0,+∞)內有唯一的零點。

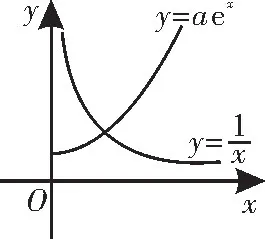
圖1

設h＇(x)的零點為x0,則。

當0＜x＜x0時,h＇(x)＜0,h(x)單調遞減;當x＞x0時,h＇(x)＞0,h(x)單調遞增。

所以h(x)min=h(x0)=-lnx0+lna=-lnx0+lna。

所以h(x)min=+x0+2lna≥2+2lna,當且僅當x0=1時取等號。

所以當x＞0 時,h(x)≥0,必須且只需2+2lna≥0,解得a≥。

所以a的取值范圍為。

10.(1)因為f(x)=,所以f(x)的定義域為(0,+∞),f＇(x)=。

令f＇(x)=0,得x=e,當x∈(0,e)時,f＇(x)＞0,f(x)在(0,e)上單調遞增。

當x∈(e,+∞)時,f＇(x)＜0,f(x)在(e,+∞)上單調遞減。

所以f(x)的遞增區間為(0,e),單調遞減區間為(e,+∞)。

又因為2022＞2021＞e,所以f(2022)＜f(2021),即,所以2021ln 2022＜2022ln2021,即ln 20222021＜ln 20212022,所以20222021＜20212022。

設f(x1)=f(x2)=m(0＜x1＜x2),則lnx1=mx1,lnx2=mx2,所以m=。

所以不等式x1·x2＞e2成立,故原不等式成立。

11.(1)令a=1,得f(x)=x2-xlnx,x＞0,所以f＇(x)=2x-lnx-1,所以f(1)=1,f＇(1)=1。

所以曲線y=f(x)在點(1,f(1))處的切線方程為y=x。

(2)因為f(x)＜-e(a+e),所以x2-axlnx＜-e(a+e),化簡得x-alnx+＜0。

因為x∈[1,e],所以x+e＞0。

令g＇(x)=0,得x=e+a。

①若e+a≤1,即a≤1-e,則g＇(x)≥0,g(x)在x∈[1,e]上單調遞增,只需g(1)=1+e2+ae＜0即可,解得a＜=-e-。

②若e+a≥e,即a≥0,則g＇(x)≤0,g(x)在x∈[1,e]上單調遞減,只需g(e)=e-a+e+a=2e＜0,此時不成立。

③若1＜e+a＜e,即1-e＜a＜0,當x∈[1,e+a)時,g＇(x)＜0,g(x)單調遞減;當x∈(e+a,e]時,g＇(x)＞0,g(x)單調遞增。

所以g(x)在x∈[1,e]上的最小值為g(e+a)=2e+a-aln(e+a),只需2e+aaln(e+a)＜0,即＞ln(e+a)。

因為1-e＜a＜0,所以＜0,0＜ln(e+a)＜1,則＞ln(e+a)不成立。

綜上可得,a的取值范圍為。

12.(1)由題意知f＇(x)=≥0恒成立,即ax2-2x+b≥0恒成立。

因為a＞0,所以Δ=4-4ab≤0,所以ab≥1,即ab的最小值為1。

所以g(t)在(0,+∞)上單調遞增,所以g(t)＞g(b2)=。

令h(b)=b--2lnb,則h＇(b)=1+＞0。

所以h(b)在(1,+∞)上單調遞增,所以h(b)＞h(1)=0,所以g(t)＞g(b2)=2h(b)＞0,即f(x1)+f(x2)+2m＞0。

13.(1)f(x)的定義域為(0,+∞),f＇(x)=+2x+(a-1)。

當a≥-3 時,f＇(x)=+2x+(a-1)≥a+3≥0,f(1)=0,所以f(x)為單調遞增函數,所以當x≥1 時,f(x)≥0 成立。

當a＜-3時,存在大于1的實數m,使得f＇(m)=0,所以當1＜x＜m時,f＇(x)＜0成立,所以f(x)在區間(1,m)上單調遞減,所以當1＜x＜m時,f(x)＜f(1)=0,所以a＜-3不可能成立。

綜上可得,a的取值范圍為[-3,+∞)。

(2)不妨設x1＜x2。

因為正實數x1,x2滿足f(x1)+f(x2)=0,由(1)可知,0＜x1＜1＜x2。

又因為f(x)為單調遞增函數,所以x1+x2＞2?x2＞2-x1?f(x2)＞f(2-x1)。

由f(x1)+f(x2)=0 得f(x2)=-f(x1),所以只需證-f(x1)＞f(2-x1),即證f(x1)+f(2-x1)＜0。

設g(x)=f(x)+f(2-x),則g(x)=2[lnx+ln(2-x)+x2-2x+1],所以g＇(x)=。

當0＜x＜1時,g＇(x)＞0,所以g(x)在(0,1)上單調遞增。

又因為g(1)=0,所以當0＜x＜1 時,g(x)＜0成立,即f(x)+f(2-x)＜0。

所以不等式f(x1)+f(2-x1)＜0 成立,所以x1+x2＞2。