導數(shù)的交匯題賞析

■江蘇省泗洪中學 祁祺

一、集合與導數(shù)的交匯

二、解三角形與導數(shù)的交匯

評注:本題考查了正弦定理、余弦定理及導數(shù)知識的運用。首先確定函數(shù)關系式,再利用導數(shù)求出最值是解題的關鍵。

三、數(shù)列與導數(shù)的交匯

例3已知函數(shù)f(x)=ax-lnx+b。

(1)若a+b=0,且f(x)≥0,求a的值;

(2)證明:ln 2+ln 3+…+ln(n+1)＞。

解析:(1)由題意知f(x)=ax-lnx-a。

當a≤0時,f＇(x)＜0,所以f(x)在(0,+∞)上遞減,又f(1)=0,所以不符合題意;

當a＞0 時,f(x)在上遞減,在上遞增,f(x)≥=1-a+lna。

令g(a)=1-a+lna,g(a)≤g(1)=0,而1-a+lna≥0,所以a=1。

(2)由(1)知,當a=1 時,f(x)=xlnx-1≥0,所以x-1≥lnx。

所以ln 2+ln 3+… +ln(n+1)＞,n∈N*。

評注:此類問題一般先由已知條件及導數(shù)得出一個不等式,再把該不等式中的自變量依次用1,2,3,…,n代換,然后用疊加法證明。

四、立體幾何與導數(shù)的交匯

例4如圖1,設三棱錐P-ABC的每個頂點都在球O的球面上,△PAB是面積為的等邊三角形,AC⊥BC,AC=BC,且平面PAB⊥平面ABC。

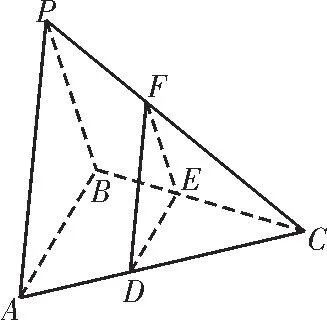
圖1

(1)求球O的表面積;

(2)證明:平面POC⊥平面ABC,且平面POC⊥平面PAB;

(3)與側(cè)面PAB平行的平面α與棱AC,BC,PC分別交于D,E,F,求四面體ODEF的體積的最大值。

解析:(1)如圖2,取AB的中點G,連接PG。

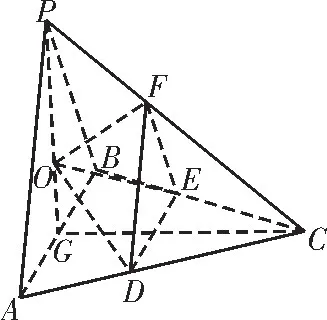
圖2

因為AC⊥BC,所以△ABC的外心為G。

因為PA=PB,所以PG⊥AB。

又平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,所以PG⊥平面ABC,所以O在PG上。

因為△PAB是等邊三角形,所以O是線段PG上靠近點G的一個三等分點。

所以球O的半徑R==2,球O的表面積為4π×R2=16π。

(2)因為O在PG上,所以PO⊥平面ABC。又PO?平面POC,所以平面POC⊥平面ABC。

如圖2,連接CG,則CG⊥AB。又平面PAB⊥平面ABC,所以CG⊥平面PAB。又CG?平面POC,所以平面POC⊥平面PAB。

(3)因為AB=,所以C到平面PAB的距離H=。

設CD=λCA(0＜λ＜1),C到平面DEF的距離為h。

因為平面PAB∥平面DEF,所以△DEF∽△ABP,則△DEF的面積為。

又h=,所以O到平面DEF的距離為。

所以V四面體ODEF==3λ2(1-λ)。

設f(λ)=3λ2(1-λ)(0＜λ＜1),則f＇(λ)=3λ(2-3λ)。

當0＜λ＜時,f＇(λ)＞0;當＜λ＜1時,f＇(λ)＜0。

所以f(λ)max=,即四面體ODEF的體積的最大值為。

評注:本題第(3)問,先求C到平面PAB的距離H。設CD=λCA(0＜λ＜1),C到平面DEF的距離為h。由平面PAB∥平面DEF,得到△DEF∽△ABP,則可得△DEF的面積,求出h=,得到O到平面DEF的距離為,則四面體ODEF的體積V=3λ2(1-λ)。轉(zhuǎn)化為函數(shù),再利用導函數(shù)求得最大值。

五、解析幾何與導數(shù)的交匯

例5已知拋物線E:y2=2px(p＞0),圓F:(x-2)2+y2=r2(r＞0),當r=時,拋物線E與圓F僅有兩個交點。

(1)求拋物線E的方程;

(2)如圖3,若圓F與拋物線E有四個交點,且交點分別是A,B,C,D,求四邊形ABCD面積的最大值。

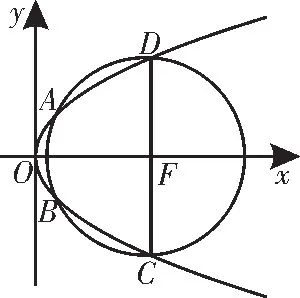
圖3

解析:(1)聯(lián)立方程組整理得x2+2(p-2)x+1=0。

(2)若圓F與拋物線E有四個交點,則方程組有四組解,得方程x2+2x+4-r2=0 有兩個不同的解,所以解得＜r＜2。

由拋物線和圓的對稱性可知,四邊形ABCD是梯形。設四邊形ABCD的面積為S,A(x1,y1),D(x2,y2)(y1,y2＞0,x2＞x1＞0),則B(x1,-y1),C(x2,-y2)。

因為x1,x2是方程x2-2x+4-r2=0的兩個不同的解,由韋達定理得x1+x2=2,x1x2=4-r2,則S=(y1+y2)(x2-x1)=。

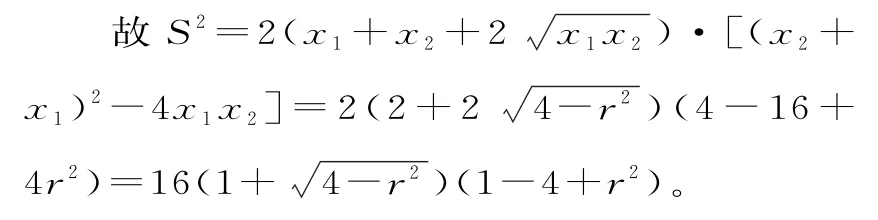
設x=,則x∈(0,1),則S2=16(1+x)(1-x2)=16(-x3-x2+x+1)。

構(gòu)造函數(shù)y=-x3-x2+x+1,x∈(0,1),則y＇=-3x2-2x+1=(-3x+1)(x+1)。

當x∈時,y＇＞0;當x∈時,y＇＜0。

所以函數(shù)y=-x3-x2+x+1 在上單調(diào)遞增,在上單調(diào)遞減。

因此當x=時,函數(shù)y=-x3-x2+x+1取得最大值,最大值為。

故當r=時,S取得最大值,最大值為。

評注:解答本題的關鍵是列出S的表達式,進一步變形為S2的表達式,運用換元法,構(gòu)造函數(shù)y=-x3-x2+x+1,x∈(0,1),再利用導數(shù)求出函數(shù)的最值。本題是一道將解析幾何與導數(shù)巧妙交匯命制的綜合性題目,難度較大。