初等函數中的“創新問題”的思維方法
■江蘇省泰興市第二高級中學 張志峰
“新定義”型問題,主要是指在問題中定義了中學數學中沒有學過的一些新概念、新運算、新符號,要求同學們讀懂題意,收集反饋處理信息,根據新的定義進行運算、推理、遷移的一種題型。這類題目具有啟發性、思考性、挑戰性和隱蔽性等特點,是考查同學們的核心素養、挖掘同學們的潛力的較佳題型,因而備受命題者的青睞。本文對初等函數中的“創新問題”的思維方法進行歸納提煉,希望對同學們的復習備考能有所幫助。
歸納1:函數值求解的“創新”——尋求函數對稱中心整體代換求解
例1已知函數f(x)=滿足條件=1,其中a>1,則=()。
A.1 B.2 C.3 D.4
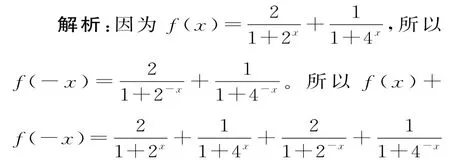

歸納2:自變量與函數值求和中的“創新”——尋求兩函數的同一對稱中心整體代換求解
例2已知f(x)=,函數g(x)對任意x∈R 有g(2018-2x)=3-g(2x-2013)成立,y=f(x)與y=g(x)的圖像有m個交點,為(x1,y1),(x2,y2),…,(xm,ym),則=()。
A.2013mB.2015m
C.2017mD.4m
解析:由g(2018-2x)=3-g(2x-2013),令t=2x-2013,則2018-2x=5-t,g(5-t)=3-g(t),可得y=g(x)的對稱中心為,而f(x)=的對稱中心為,所以y=f(x)與y=g(x)的圖像有m個交點(x1,y1),(x2,y2),…,(xm,ym)關于對稱,所以x1+xm=x2+xm-2=x3+xm-3=…=5,y1+ym=y2+ym-2=y3+ym-3=…=3。設x1+x2+…+xm-1+xm=M,則xm+xm-1+…+x2+x1=M,兩式相加可得(x1+xm)+(x2+xm-2)+…+(xm-1+x2)+(xm+x1)=2M=5m,所以M=。同理可得y1+y2+…+ym-1+ym=。=x1+x2+…+xm+y1+y2+…+ym==4m。故選D。
提煉:利用換元法探究函數的對稱中心是本題的一個創新,求兩函數交點的自變量與函數值的和,探究兩函數的同一對稱中心,利用函數的對稱中心整體簡化求解是本題的另一個創新。
歸納3:超越方程根的“創新”——借助指數函數和對數函數的對稱性尋求切入
例3已知方程2018x=a-x和方程log2018x=a-x(a>1)的根分別為x1,x2,則的取值范圍為()。


提煉:指數函數、對數函數與同一個一次函數構成的方程的根,利用互為反函數其圖像關于直線y=x對稱探究兩根的關系,選主元挖掘隱含條件,構建函數求解范圍問題。
歸納4:函數不等式探究中的“創新”——函數的單調性和奇偶性的合理轉化
例4已知函數f(x)=2x且f(x)=g(x)+h(x),其中g(x)為奇函數,h(x)為偶函數。若不等式3ag(x)+h(2x)≥0對任意x∈[1,2]恒成立,則實數a的取值范圍為_____。
解析:由已知得g(x)+h(x)=2x,注意g(x)為奇函數,h(x)為偶函數,則g(-x)+h(-x)=2-x。又因為g(x)為奇函數,h(x)為偶函數,所以-g(x)+h(x)=2-x。所以h(x)=,g(x)=,代入不等式3ag(x)+h(2x)≥0,得≥0在[1,2]上恒成立。
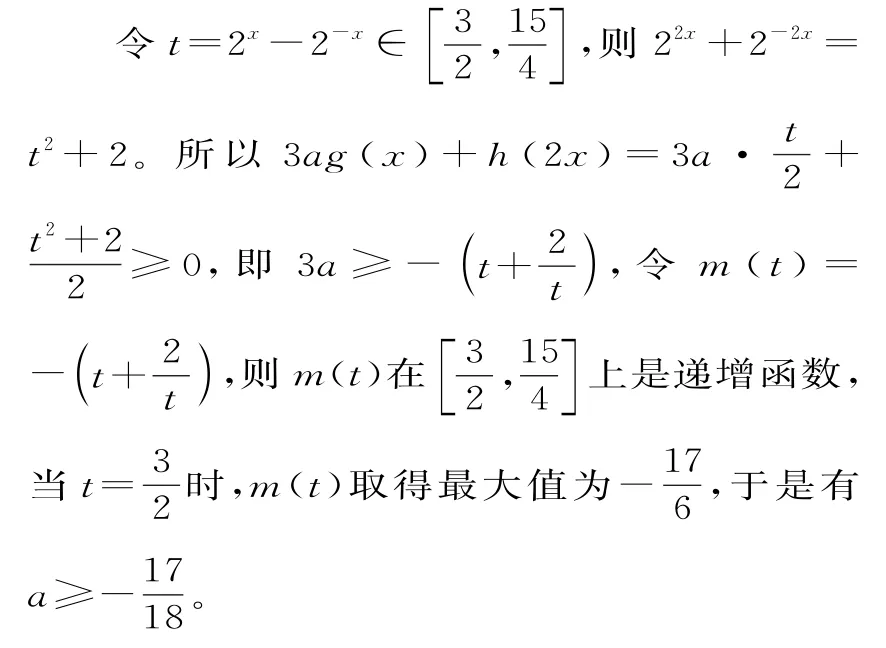
提煉:利用奇偶性構建方程組是本題的一個創新,揭示了定義域關于原點對稱的函數都可以寫成一個奇函數與一個偶函數的和。函數不等式問題可以轉化為含指數變量的不等式恒成立問題,分離參數轉化為新函數的值域問題,換元法轉化為對勾函數的單調性問題,是待定系數法、構造法、換元法等解題方法的交匯創新。
歸納5:等高線下的最值“創新”——由函數圖像探究自變量的關系降元構造函數求解
例5(2021年河北衡水中學一調)已知存在x2>x1≥0,使得f(x1)=f(x2),則x1f(x2)的取值范圍為_____。
解析:作出函數f(x)=的圖像,如圖1所示。
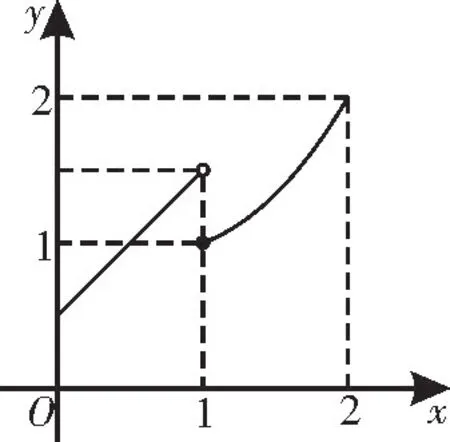
圖1
因為存在x2,x1,當x2>x1≥0 時,f(x1)=f(x2),所以0≤x1<1。

提煉:對于分段函數或不同函數,當函數值相等時,利用對應自變量滿足的關系式求最值,這是等高線下的最值創新。這類問題既要注意等高線隱含的范圍,同時還要挖掘等高線下自變量之間的關系,合理地選擇主元構建函數在區間上的最值求解。本題關鍵在于如何求出≤x1<1。
歸納6:復合函數不等式的“創新”——借助分段函數的圖像和性質簡化求解
例6若則不等式f(2x2-|x|)≤5的解集為____。
解析:如圖2,當x<0 時,f(x)=-x2+x+2=<2,且函數為增函數;

圖2
當x≥0時,f(x)=x2+3x+1=≥1,且函數為增函數。
(1)若2x2-|x|<0,則不等式f(2x2-|x|)≤5恒成立,此時|x|(2|x|-1)<0,解得0<|x|<。
(2)若2x2-|x|≥0,即|x|≥或|x|≤0,則不等式f(2x2-|x|)≤5恒成立。
因為f(1)=5,所以不等式f(2x2-|x|)≤5等價于f(2x2-|x|)≤f(1),則2x2-|x|≤1,即2x2-|x|-1≤0,則|x|≤1。
因為|x|≥或|x|=0,所以≤|x|≤1或|x|=0。
由(1)和(2)知|x|≤1,所以不等式f(2x2-|x|)≤5的解集為[-1,1]。
提煉:關于分段函數的復合函數不等式問題,屬于函數圖像和性質應用的創新,求解的關鍵在于整體變量的“對號入座”,運用解析式和單調性作出分段函數的圖像,便于尋找分界點和討論函數的單調性,注意整體變量觀念可避免多解或漏解的發生。

