函數性質應用中的“數學素養”

■江蘇省泰興市第二高級中學 李明

函數性質是整個高中數學的核心內容,是高中數學的主線,所有知識均可與函數建立聯系,都可圍繞這一主線展開,函數的單調性、奇偶性和周期性更是高考考查的重中之重,常與方程、不等式等知識結合起來考查,本文探究函數性質應用中的“數學素養”。

一、抽象函數性質探究中的“思維方法”

例1(2021年江蘇省蘇州市高新區第一中學高三月考)已知定義在R 上的函數f(x)滿足:對任意x,y∈R,都有f(x+y)=f(x)+f(y),且當x＞0時,f(x)＞0。

(1)求f(0)的值,并證明f(x)為奇函數;

(2)判斷函數f(x)的單調性,并證明;

(3)若f(k·2x)+f(4x+1-8x-2x)＞0對任意x∈[-1,2]恒成立,求實數k的取值范圍。

解析:(1)令x=y=0,得f(0+0)=f(0)+f(0),所以f(0)=0。

令y=-x,得f(x-x)=f(x)+f(-x)=f(0)=0,所以f(-x)=-f(x),故f(x)為奇函數。

(2)設x2＞x1,則x2-x1＞0。

由f(x2)=f(x1+x2-x1)=f(x1)+f(x2-x1)?f(x2-x1)=f(x2)-f(x1)。

因為當x＞0時,f(x)＞0,所以f(x2-x1)=f(x2)-f(x1)＞0?f(x2)＞f(x1)。

所以f(x)是增函數。

(3)由題知f(k·2x+4x+1-8x-2x)＞0。

又y=f(x)是定義在R 上的增函數,所以k·2x+4x+1-8x-2x＞0 對任意x∈[-1,2]恒成立,所以k·2x＞2x+8x-4x+1,所以k＞1+22x-2x+2。

令2x=t,t∈,則f(t)=t2-4t+1,所以k＞f(t)max。

當t=4時,f(t)max=f(4)=16-16+1=1,所以k＞1。

體驗:對于抽象函數的有關問題,其求解的思維方法是:合理運用對應法則和題設條件,多次賦值探究奇偶性;依據定義、題設及法則證明其單調性;利用奇偶性和單調性轉化為函數不等式,通過不等式恒成立求參數的取值范圍;常用變量分離法、換元法、構造函數法等求最值。主要考查同學們的數學運算、構建函數模型及邏輯推理等能力。

二、函數對稱性應用中的“整體思維”

例2(2021 年湖南省衡陽市雁峰區校級月考)已知函數f(x)=。

(1)求證:存在定點M,使得函數f(x)的圖像上任意一點P關于點M對稱的點Q也在函數f(x)的圖像上,并求出點M的坐標;

(3)對于(2)中的Sn,求證:對于任意的n∈N*,都有lnSn+2-lnSn+1＞。

解析:(1)函數f(x)的定義域為(0,1)。設M(a,b),若使得函數f(x)的圖像上任意一點P關于點M對稱的點Q也在函數f(x)的圖像上,則必有f(x)+f(2a-x)==2b,對于x∈(0,1)恒成立,所以1-2a=0,1=2b,所以a=b=。所以存在定點,使得函數f(x)的圖像上任意一點P關于點M對稱的點Q也在函數f(x)的圖像上。

(2)由(1)得f(x)+f(1-x)=1。

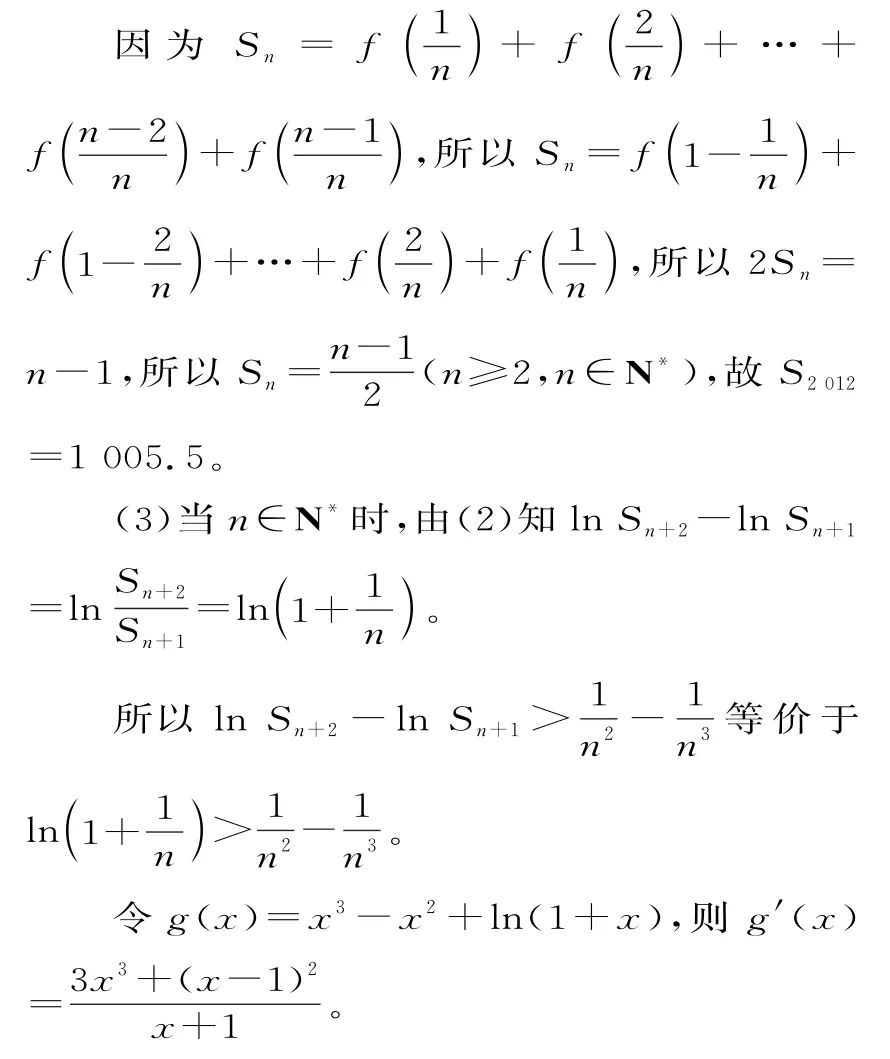
所以當x∈(0,+∞)時,g＇(x)＞0,即函數g(x)在(0,+∞)上單調遞增,又g(0)=0,所以g(x)＞g(0)=0,即x3-x2+ln(1+x)＞0恒成立。

故當x∈(0,+∞)時,有ln(1+x)＞x2-x3成立,取x=∈(0,+∞),則有成立。

體驗:當函數f(x)滿足f(x+a)+f(b-x)=c時,函數y=f(x)的圖像關于點對稱;利用“函數的對稱中心的特征,采用倒序相加法整體思維”可簡化求解函數值構成的數列的求和問題。對于函數不等式的證明,可用分析綜合法轉化為函數值的大小關系,構造新函數研究單調性進行求證。凸顯函數性質應用中的邏輯推理、整體思維、構建函數模型等素養。

三、最值探究中的“換元法和分類討論”

例3(2022 屆東北育才學校科學高中部高三第一次模擬)已知函數f(x)=+(sinx+cosx)·(sinx-cosx)+1。

(1)常數ω＞0,若函數y=f(ωx)在區間上是增函數,求ω的取值范圍;

(2)若函數g(x)=-1 在上的最大值為2,求實數a的值。

解析:(1)利用三角恒等變換公式化簡得f(x)=+sin2xcos2x+1=2(1-sinx)sinx+sin2x-cos2x+1=2sinx,則y=f(ωx)=2sin(ωx)。

故ω的取值范圍為(0,1]。

(2)由(1)可得g(x)=-1=sin 2x+a(cosx-sinx)--1,x∈。

設t=cosx-sinx,則sin 2x=2sinxcosx=1-t2。

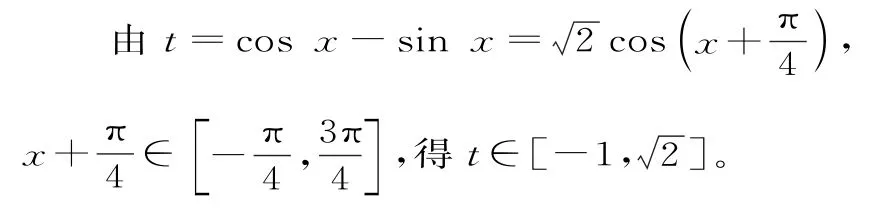
綜上,實數a的值為-2或。

體驗:三角公式±sinxcosx=,揭示了二次函數關系,同時給出了“平方溝通的三角變換方法”,奠定了換元法化歸構造外層為二次函數在區間上的最值,借助對稱軸和區間分類研究最值問題。形如y=asin2x+bsinx+k,可先設sinx=t,轉化為關于t的二次函數求值域;形如y=asinxcosx+b(sinx±cosx)+c,可先設t=sinx±cosx,轉化為關于t的二次函數求值域。利用換元法處理三角函數的最值時,注意確定新元范圍,如令t=sinx,t∈[-1,1];t=sinx+cosx,t∈等。

四、復合函數開放探索研究中的“推理驗證”

例4(2021 年江蘇省淮安市洪澤區高三月考)現有如下三個條件:在①f(x)+f(-x)=0;②f(x)-f(-x)=0;③f(-2)=-f(2)。從這三個條件中選擇一個,補充在下面問題中,并給出解答。

已知函數f(x)=(a∈R)滿足____。

(1)求a的值;

(2)若函數g(x)=2f(-x)+1-,證明:g(x2-x)≤。

解析:選擇條件①f(x)+f(-x)=0。

選擇條件②f(x)-f(-x)=0。

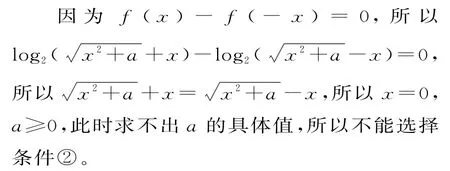
選擇條件③f(-2)=-f(2)。

體驗:復合函數研究中的開放探索,按照題設要求合理選擇條件,一一進行推理驗證,推理驗證過程中涉及奇偶函數的特征、對數運算及復合函數的最值探究。