一種城市公共自行車系統(tǒng)調(diào)度優(yōu)化模型

邵 卿

（湖南鐵路科技職業(yè)技術(shù)學(xué)院，湖南株洲 412000）

城市公共自行車系統(tǒng)有助于解決城市交通擁堵和公共交通出行“最后一公里”難題，但系統(tǒng)運(yùn)轉(zhuǎn)過程中需要解決車輛的周轉(zhuǎn)調(diào)度問題。蔣塬銳等[1]針對共享單車供需失衡、共享率低等問題，以提高用車高峰期調(diào)度的及時(shí)性為目的，在調(diào)度結(jié)構(gòu)中引入調(diào)度池，明確調(diào)度池的使用規(guī)則，提出共享單車四級調(diào)度結(jié)構(gòu)，考慮節(jié)點(diǎn)的調(diào)度需求大于調(diào)度車的裝載容量和多輛調(diào)度車共同滿足單個(gè)節(jié)點(diǎn)的調(diào)度需求的情況，以調(diào)度總成本最小為目標(biāo)，建立共享單車靜態(tài)調(diào)度模型。李軍等[2]將公共自行車顧客借、還車輛的過程看作排隊(duì)現(xiàn)象，完整描述排隊(duì)系統(tǒng)的輸入、輸出過程及排隊(duì)規(guī)則和服務(wù)方式，利用實(shí)例車輛借還數(shù)據(jù)，標(biāo)定顧客借還車的到達(dá)及站點(diǎn)服務(wù)時(shí)間均服從負(fù)指數(shù)分布，基于損失制排隊(duì)系統(tǒng)效率指標(biāo)計(jì)算方法，建立站點(diǎn)最優(yōu)化車輛調(diào)配數(shù)（空樁數(shù)）計(jì)算模型。李迎晨等[3]提出基于遺傳算法的公共自行車高峰期調(diào)度模型，可以滿足早晚高峰居民出行的自行車需求。高亮等[4]為提高公共自行車系統(tǒng)調(diào)度效率并降低調(diào)度成本，提出基于預(yù)測庫存變化率的公共自行車動(dòng)態(tài)調(diào)度方法，建立優(yōu)化目標(biāo)為車輛總行駛距離最短的動(dòng)態(tài)調(diào)度模型。于德新等[5]針對現(xiàn)有自行車調(diào)度模型假設(shè)條件的局限性，提出共享經(jīng)濟(jì)模式下轉(zhuǎn)運(yùn)最大化策略，在詳細(xì)分析共享單車調(diào)度成本及相關(guān)參數(shù)的基礎(chǔ)上，以成本最小和投放率最高為目標(biāo)建立共享單車調(diào)度模型，引入精英策略和進(jìn)化算子對遺傳算法進(jìn)行改進(jìn)，采用TOPSIS法在改進(jìn)算法求解出的有效路線集中選擇最優(yōu)路線。

1 模型構(gòu)建

模型規(guī)劃描述了確定待建租賃點(diǎn)和各點(diǎn)的調(diào)配量的情況下，規(guī)劃調(diào)度車輛的路線安排和分配，使總運(yùn)輸成本最小。待建的站點(diǎn)編號被定為j(j∈J1)，將車場編號定為0；設(shè)運(yùn)輸車輛編號定為v(v∈V)，建立模型：)，目標(biāo)為總運(yùn)輸成本最小，包括固定成本和可變成本。

設(shè)定約束條件：

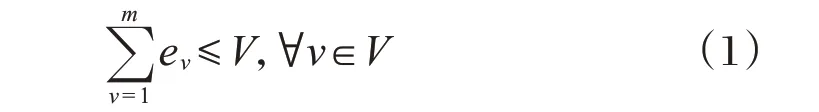
限制調(diào)度車數(shù)量。

限制調(diào)度車的運(yùn)輸容量。

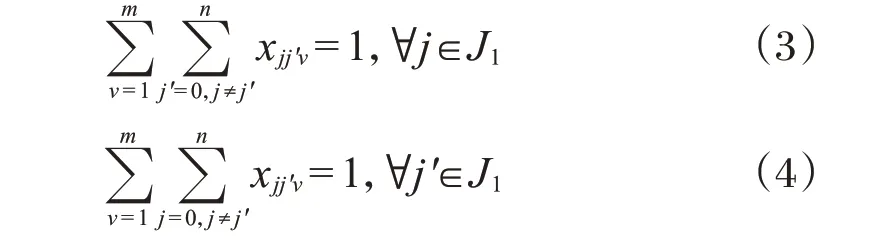
各站點(diǎn)都被服務(wù)，且一輛車僅服務(wù)一次。

車輛v為租賃點(diǎn)j調(diào)度服務(wù)的決策變量，車輛v在租賃點(diǎn)j′結(jié)束調(diào)度工作后，再到租賃點(diǎn)j進(jìn)行調(diào)度，則xjj′v=1，否則xjj′v=0。

運(yùn)輸車輛v運(yùn)輸路徑的決策變量，若車輛v被使用，則ev=1，否則ev=0。

2 算例分析

2.1 算例簡介

擬在某規(guī)劃區(qū)域內(nèi)建設(shè)一個(gè)公共自行車租賃系統(tǒng)，進(jìn)行自行車調(diào)運(yùn)工作，根據(jù)居民的出行需求確定10個(gè)自行車出行需求點(diǎn)，分配相應(yīng)數(shù)量的自行車和停車樁，以滿足居民的出行需求，做到任一時(shí)段居民在其步行范圍內(nèi)的租賃點(diǎn)均能夠借到車和還出車，使規(guī)劃區(qū)域內(nèi)居民總出行時(shí)間最短。但租賃點(diǎn)的建設(shè)數(shù)目應(yīng)為7～13，避免租賃點(diǎn)建設(shè)太多造成資源的浪費(fèi)以及租賃點(diǎn)建設(shè)過少無法滿足出行者的需求。

候選租賃點(diǎn)和需求點(diǎn)之間的距離如表1所示。

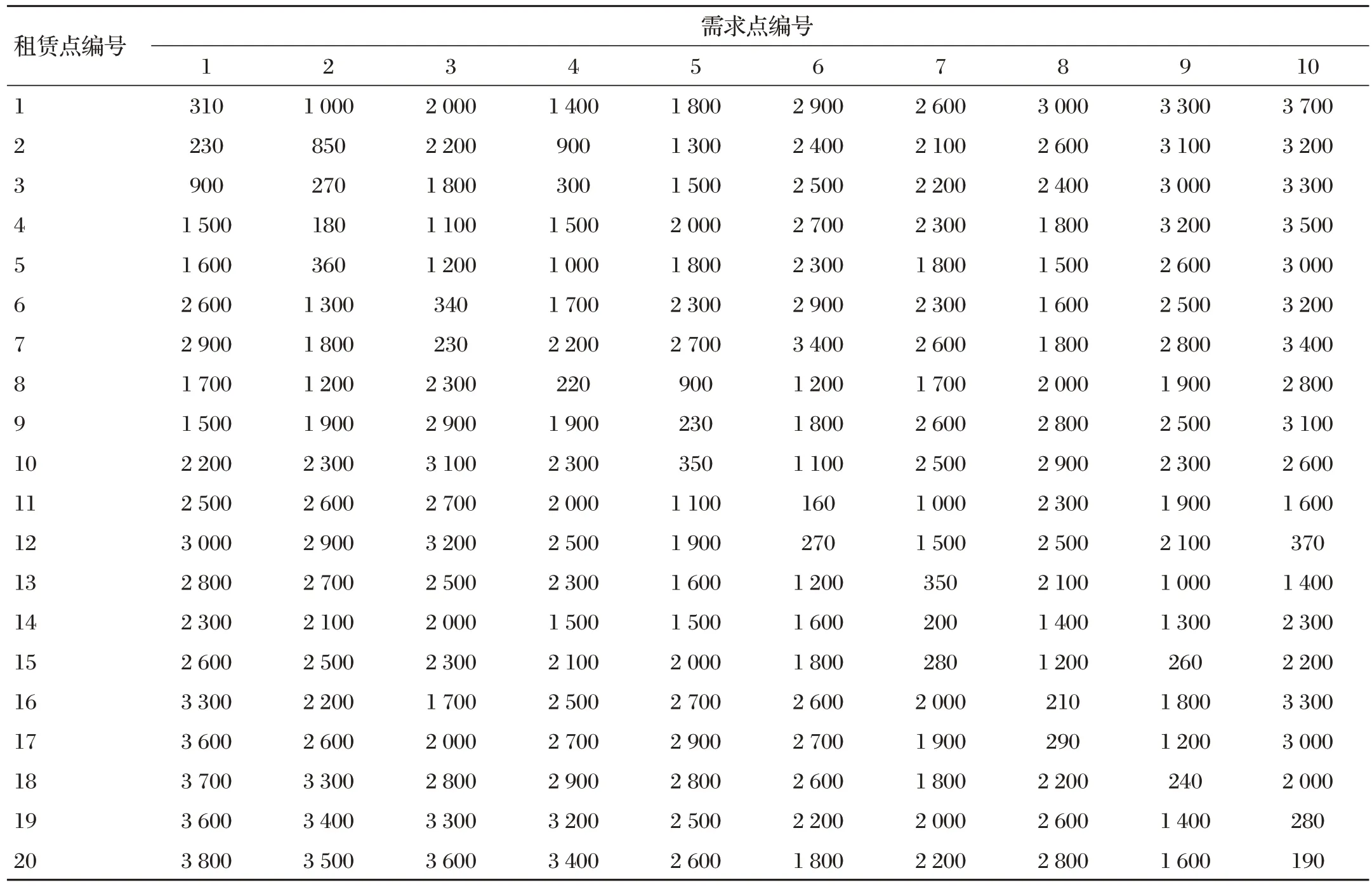
表1 候選租賃點(diǎn)和需求點(diǎn)之間的距離 單位：m

時(shí)段1各個(gè)需求點(diǎn)的公共自行車租借需求如表2所示。

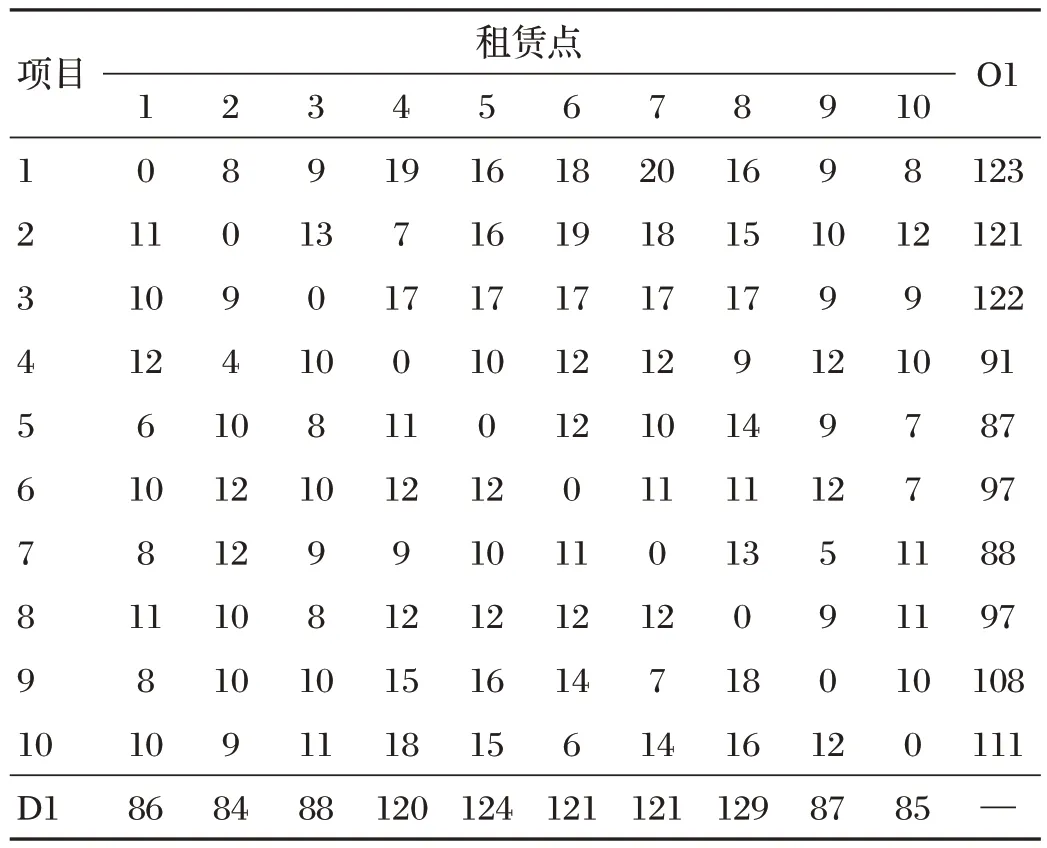
表2 公共自行車租借需求

算例運(yùn)算思路邏輯圖如圖1所示。

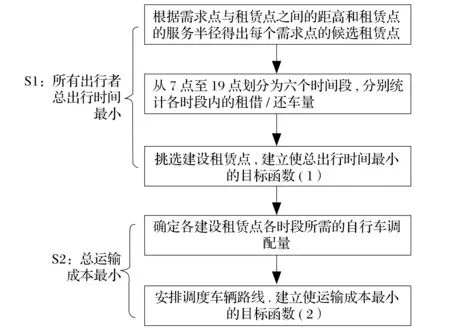
圖1 算例運(yùn)算思路邏輯圖

2.2 算例求解

（1）相關(guān)常量取值。

C=400 m、M=10 000、g=50 000元、α=15輛、f1=300元、f2=2 000元、v1=1.4 m/s、v2=5 m/s、V=2輛、p=2元/km、r=40元、Q=100輛。

（2）根據(jù)租賃點(diǎn)與需求點(diǎn)間的距離以及租賃點(diǎn)的服務(wù)半徑C可得每個(gè)需求點(diǎn)對應(yīng)的候選租賃點(diǎn)。

需求點(diǎn)對應(yīng)的候選租賃點(diǎn)如表3所示。

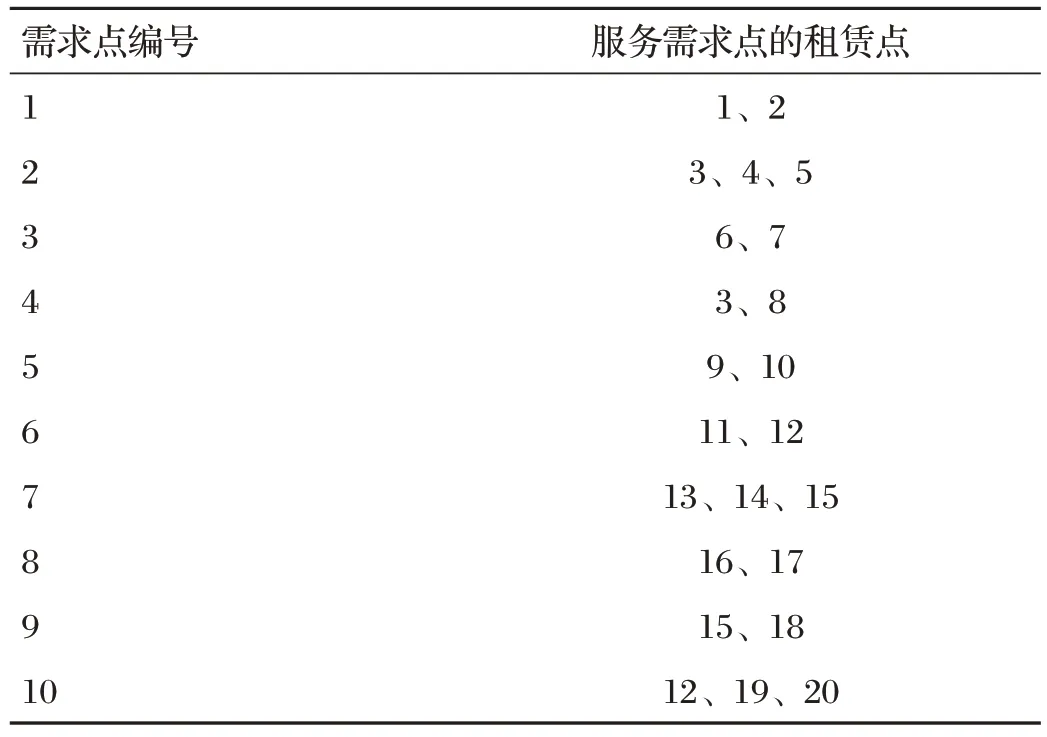
表3 需求點(diǎn)對應(yīng)的候選租賃點(diǎn)

（3）運(yùn)用LINGO編程求解，運(yùn)行該程序計(jì)算規(guī)劃區(qū)域內(nèi)居民最短的總出行時(shí)間為4 096 021秒，運(yùn)輸成本為363.5元，共需建設(shè)13個(gè)租賃點(diǎn)，編號分別為2、4、6、7、8、9、11、14、16、17、18、19、20。

租賃點(diǎn)應(yīng)分配的自行車數(shù)和停車樁數(shù)如表4所示。

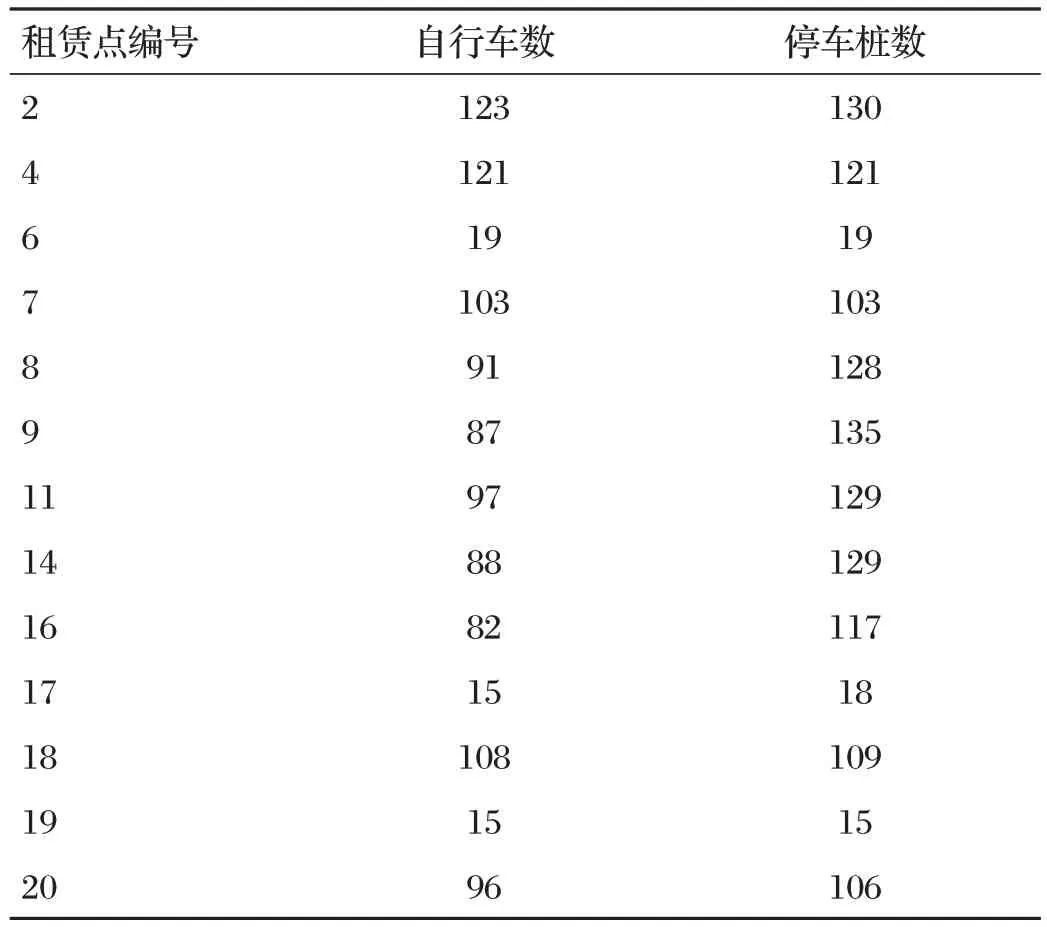
表4 租賃點(diǎn)應(yīng)分配的自行車數(shù)和停車樁數(shù)

依據(jù)選址方案及租賃點(diǎn)和需求點(diǎn)之間的距離表可得到各建設(shè)的站點(diǎn)應(yīng)服務(wù)的需求點(diǎn)和調(diào)度車輛路徑。調(diào)度車輛運(yùn)行路徑為2→4→6→7→16→17→14→18→19→20→11→8→9。

各租賃點(diǎn)各時(shí)段的調(diào)配量見表5。

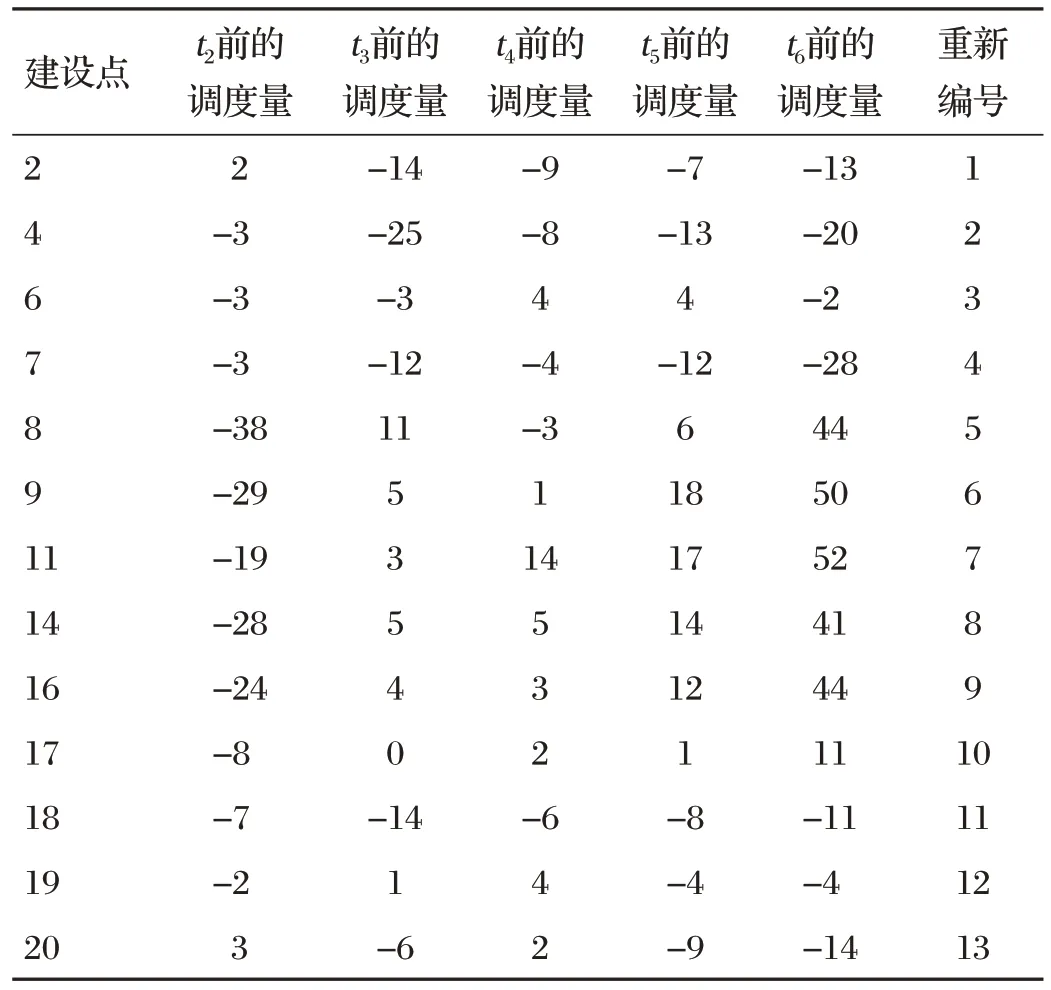
表5 各租賃點(diǎn)各時(shí)段的調(diào)度量

租賃點(diǎn)服務(wù)需求點(diǎn)和調(diào)度車輛路徑如圖2所示。

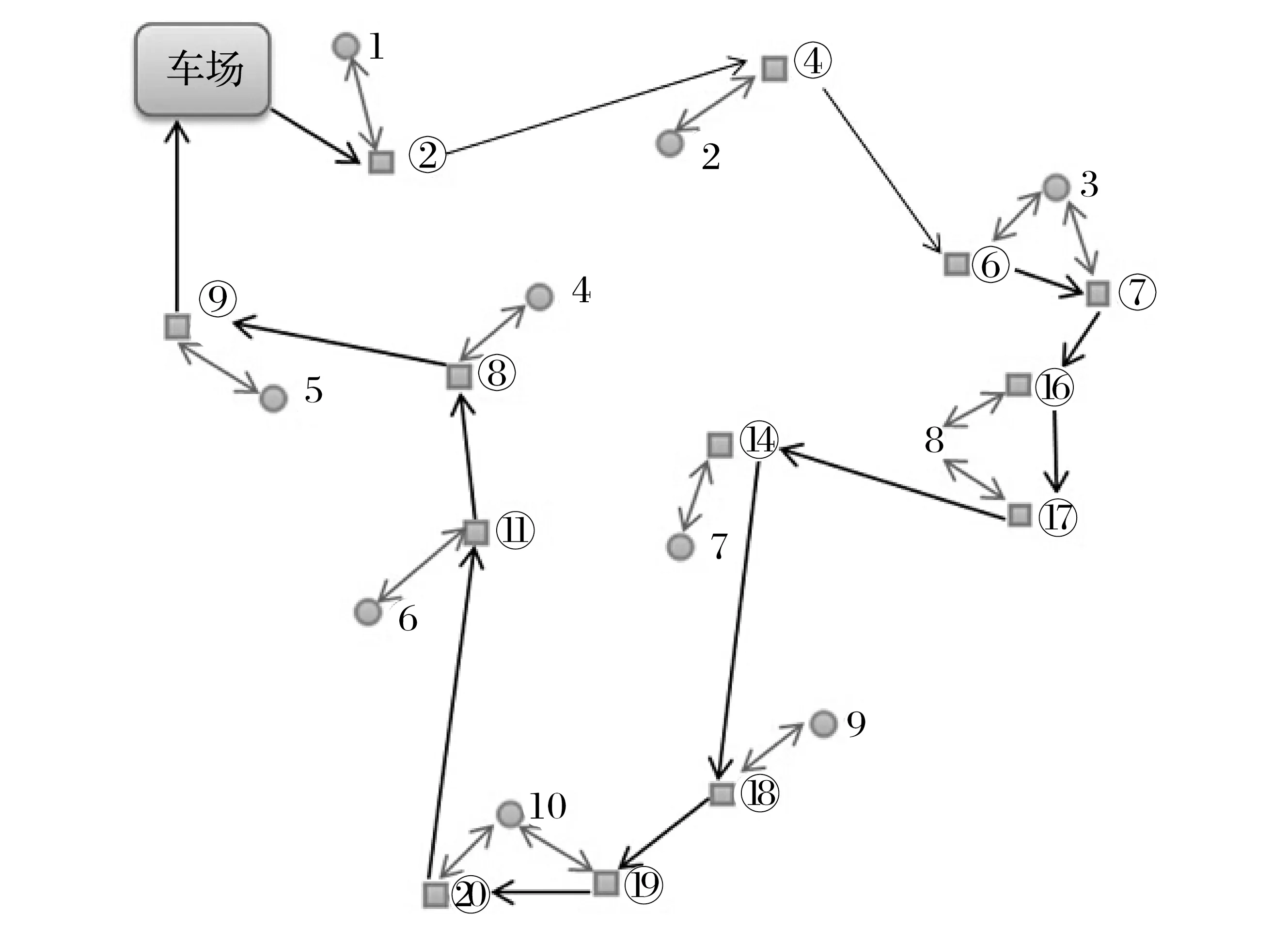
圖2 租賃點(diǎn)服務(wù)需求點(diǎn)和調(diào)度車輛路徑

3 結(jié)語

本文研究城市公共自行車系統(tǒng)調(diào)度優(yōu)化問題，基于問題分析建立相關(guān)的函數(shù)關(guān)系，構(gòu)建公共自行車調(diào)度優(yōu)化模型供科學(xué)決策參考，未來可以考慮將研究對象的范圍由本文適用的小區(qū)擴(kuò)大至街區(qū)。