基于CBLRE模型的軸向柱塞泵空化狀態檢測研究*

李志杰,蘭 媛,2*,黃家海,2,牛藺楷,2,袁科研,范佳祺,武 兵,2

(1.太原理工大學 機械與運載工程學院,山西 太原 030024;2.太原理工大學 新型傳感器與智能控制教育部重點實驗室,山西 太原 030024)

0 引 言

因結構緊湊、功率密度高且壽命長,目前,軸向柱塞泵在各種機械設備中得到了廣泛應用。然而,空化現象的產生制約了柱塞泵向高速高壓方向的進一步發展[1]。

在標準大氣壓下,液壓油中會不可避免地含有一部分空氣,當壓力降低到空氣分離壓時,空氣會從液體中析出,并聚集成氣泡游離于流體中。壓力越低,析出的空氣越多,形成的氣泡直徑越大,甚至形成空泡團[2],這些空泡會在泵內高壓區發生潰滅,從而產生局部高溫,同時也會對泵體產生沖擊。輕微的空化會導致柱塞泵振動的加劇,并導致其內部的局部區域發生空蝕破壞,最終降低其機械性能[3];當空化嚴重到一定程度時,甚至會引發安全事故。

所以,對柱塞泵的空化狀態進行有效檢測可以提高整個液壓系統的性能,其意義重大。

為有效識別空化狀態,國內外相關研究人員已經開展了大量研究。

(1)國內方面。在嚴重空化、側板磨損和齒輪磨損3種運行狀態下,姚春江等人[4]研究了齒輪泵各頻段小波包能量熵的變化規律。采用頻譜分析的方法,駱斌等人[5]研究了離心泵正常和汽蝕運行狀態的外特性,結果表明,空化現象會引發泵體的共振,擴大其共振的頻率范圍,且其振動幅值會隨著空化程度的加劇而增大。賀國等人[6]提出了一種基于改進倍頻帶特征的空化狀態識別方法,并采用BP神經網絡,對4種不同程度揚程下降的泵體的空化狀態進行了識別。段向陽等人[7]采用水聽器,采集了離心泵發生空化時的高頻輻射噪聲信號,通過對高頻輻射噪聲信號進行分析,得到了典型的空化聲壓變化規律。曹玉良等人[8]搭建了一種棧式自編碼網絡(SAE),并對離心泵的不同空化狀態進行了實驗識別,實驗結果表明,該方法對弱空化狀態有較好的識別效果。陳保家等人[9]采用CNN-LSTM混合神經網絡,對滾動軸承進行了智能故障診斷,直接從滾動軸承的原始振動信號中自適應地提取出了故障特征信息。孫娜等人[10]采用正則化超限學習機(RELM),對金沙江控制站的日徑流進行了預測。

(2)國外方面。AL-OBAIDI A R[11]利用振動信號的均值和均方根值,對離心泵內汽蝕的產生和發展進行了預測。NASIRI M R等人[12]從離心泵不同空化程度的振動信號中提取到了多種統計特征,并將其作為多隱層神經網絡的輸入,為離心泵的狀態監測提供了一種智能化方法。TIWARI R和BORDOLOI D J等人[13]將離心泵壓力信號的幾種時域統計特征進行組合,然后將其作為卷積神經網絡的輸入進行了訓練,成功識別了不同轉速下離心泵堵塞和空化的嚴重程度。

雖然上述研究都在空化狀態的識別方面取得了顯著成果,但其研究對象大部分為水力機械,其設備的傳輸介質主要是水,且水泵與液壓泵在結構和工作原理上也有較大差異。

所以,在柱塞泵空化現象的研究方面,結合深度學習網絡與非線性分類器的優點,筆者提出一種基于CBLRE(CNN+BiLSTM+RELM)模型的柱塞泵空化狀態識別方法(檢測模型),即利用卷積神經網絡(CNN)提取信號特征,利用雙向長短期記憶(Bi-LSTM)網絡學習特征序列的時間依賴性,利用正則化極限學習機(RELM)的非線性分類器進行分類。

該模型結合深度學習網絡與非線性分類器的優點,直接利用一維原始振動信號,對柱塞泵空化現象進行狀態識別。

1 CBLRE模型理論

1.1 CNN提取特征的基本原理

CBLRE模型的特征提取由卷積神經網絡(CNN)層來完成。CBLRE模型通過多層次的非線性映射關系,學習柱塞泵振動信號的深層特征。

CNN最重要的部分為卷積池化層,其相鄰層之間采用局部連接和權值共享的方式進行運算,自動提取輸入信號的局部特征。

通過卷積運算可以得到具有旋轉和平移不變性的分類特征,其計算過程如下:

(1)

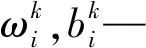
卷積運算后,為加速模型的收斂,并防止其過擬合,CNN通常采用ReLU函數作為激活函數,以獲得其非線性特征。同時,為了減少特征維數和網絡參數,通常會在卷積層之后增加池化層,以此來進行下采樣。

常用的池化方式有兩類,即平均池化和最大池化。筆者采用最大池化的方式來計算特征矩陣的局部極值,縮減數據維度。

其計算過程如下:

(2)

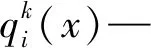
其中:x∈[(j-1)N+1,jN],N—池化區域的寬度。

1.2 BiLSTM層的基本原理

由于CBLRE模型僅僅是利用CNN網絡來提取振動信號的局部特征,而不是其最終表示,還需要利用RNN網絡來學習特征序列的時間依賴性[14]。

雙向長短時記憶(BiLSTM)網絡彌補了LSTM網絡只能學習到前向歷史信息的缺陷。它可以綜合利用時間序列的兩向歷史信息,因此,有效提高了LSTM網絡的學習能力[15]。

雙向長短時記憶網絡是由連接著同一個輸出層的前向LSTM層和后向LSTM層構成,其輸出為前后兩向LSTM層輸出之和[16]。

兩向LSTM層的結構和計算方法均相同,但兩向LSTM層中神經元的權值不能共享[17，18]。

雙向長短時記憶網絡的具體結構如圖1所示。

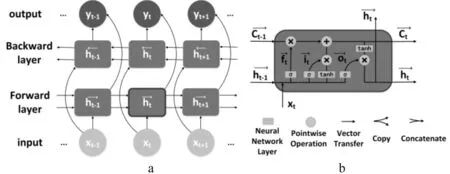
圖1 雙向長短時記憶網絡結構圖

圖1中,LSTM隱層神經元主要由遺忘門、輸入門和輸出門3個門結構構成。

由CNN層提取的局部特征信息輸入到LSTM單元后,通過遺忘門對作用小的信息進行選擇性遺忘。

其計算公式如下:

通過輸入門選擇加入到記憶單元的新信息,并更新記憶單元,即:

ft=σ(ωxfxt+ωhfht-1+bf)

(3)

式中:ωxf,ωhf,bf—遺忘門的權重矩陣和偏置。

信息it的表達式為:

it=σ(ωxixt+ωhiht-1+bi)

(4)

式中:ωxi,ωhi,bi—輸入門的權重矩陣和偏置。

(5)

式中:ωxc,ωhc,bc—記憶單元的權重矩陣和偏置。

當前時刻的記憶單元ct的表達式為:

(6)

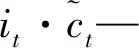
最終,輸出ht由輸出門的輸出ot與記憶單元ct共同決定,其計算公式如下:

ot=σ(ωxoxt+ωhoht-1+bo)

(7)

式中:ωxo,ωho,bo—輸出門的權重矩陣和偏置;xt—當前輸入;ht-1—前一個單元的輸出。

當前單元的輸出ht的表達式為:

ht=ot·tanh(ct)

(8)

1.3 RELM的基本原理

CBLRE模型在學習到振動信號的多層次信息后,利用非線性分類器進行故障識別,可以有效避免線性分類器存在的局限。

HUANG G B等人[19]提岀了一種結構簡單、學習速度快,且泛化能力強的單隱層前饋神經網絡—ELM(extremel learning machine)。然而,ELM模型在利用最小二乘損失函數構建時,僅僅考慮了模型的經驗風險,沒有考慮模型的結構風險,從而使其極易產生過擬合。

為此,有研究者將正則系數引入ELM模型,構建出了正則化極限學習機(RELM)模型,大大提高了ELM模型的泛化能力[20]。

RELM模型優化的目標函數為:

(9)

式中:‖ε‖2,‖β‖2—經驗風險和結構風險;C—正則化系數;ε—訓練誤差和。

其中,訓練誤差和ε的計算公式為:

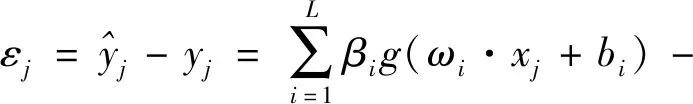
(10)

式中:x—輸入;y—期望輸岀;g(x)—隱含層神經元的激活函數,最為常用的是sigmoid函數;L—隱層神經元個數;N—樣本個數;ωi—連接輸入神經元和第i個隱層神經元的輸入權重;bi—第i個隱層神經元的閾值;βi—連接第i個隱層神經元與輸岀神經元的輸岀權重。

此處引入拉格朗日乘子λ,構建拉格朗日方程,即:

(11)

分別對上式求偏導,求解出輸岀權重矩陣為:

β=[HTH+I/C]+HTY

(12)

式中:I—單位矩陣;H—隱含層的輸出矩陣;[HTH+I/C]+—矩陣HTH+I/C的廣義逆摩爾矩陣。

最終得到RELM的預測結果為:

(13)

2 基于CBLRE模型的空化識別方法

2.1 模型概況

CBLRE診斷模型由原始信號層、濾波器層、BiLSTM層,以及非線性分類輸出層組成,其具體結構如圖2所示。

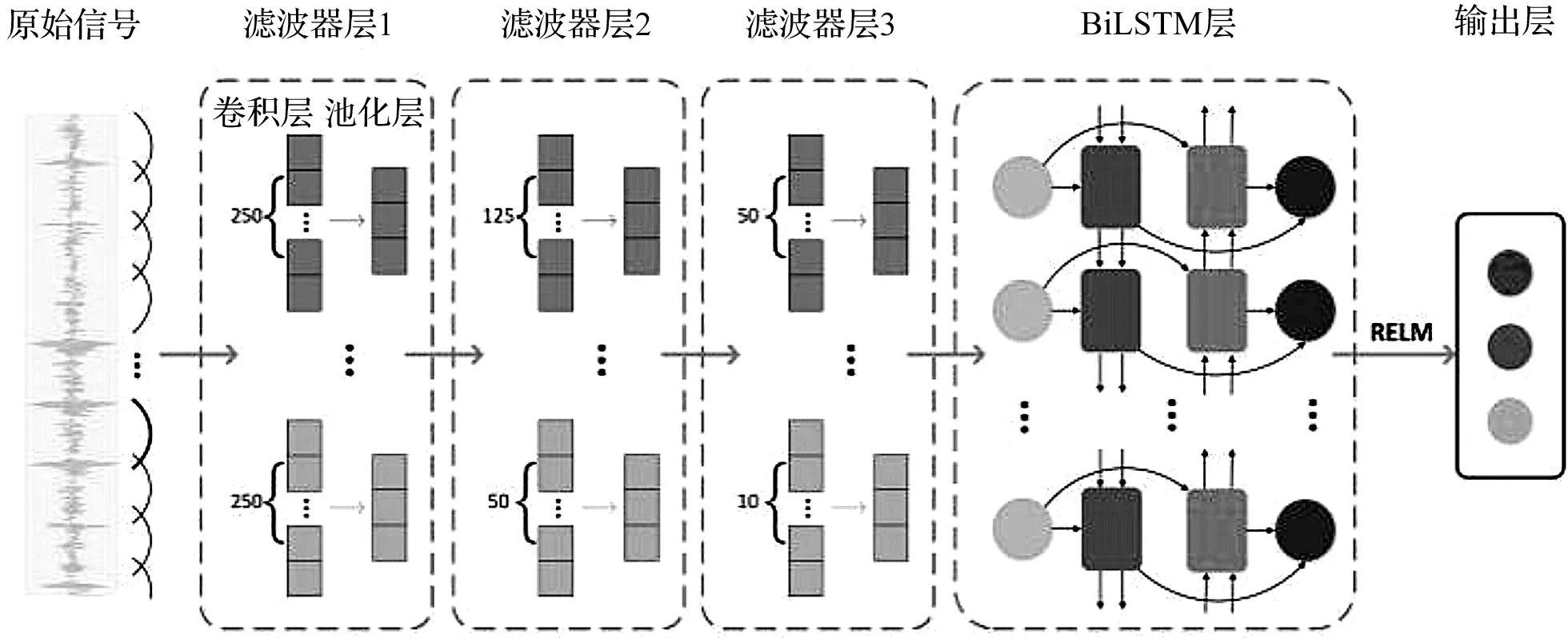
圖2 CBLRE模型結構圖

從圖2可以看出,基于CBLRE模型的柱塞泵空化狀態識別流程如下:

(1)對一維原始振動信號進行數據增強以及標準化處理,并輸入到濾波器層;

(2)濾波器層會對輸入信號進行多次卷積與池化運算,自動提取信號特征并進行特征降維;但濾波器層提取的多尺度抽象特征缺少時間關聯性,所以其將輸入到BiLSTM層,讓模型從前后兩向學習特征序列的時間依賴性;

(3)使用RELM非線性分類器對空化狀態進行識別,完成故障診斷。

2.2 實驗臺及數據采集

為了有效檢測柱塞泵的空化[21，22]狀態,在37 kW的液壓工作站上,筆者搭建了柱塞泵的空化實驗臺。

柱塞泵空化實驗臺的原理圖如圖3所示。

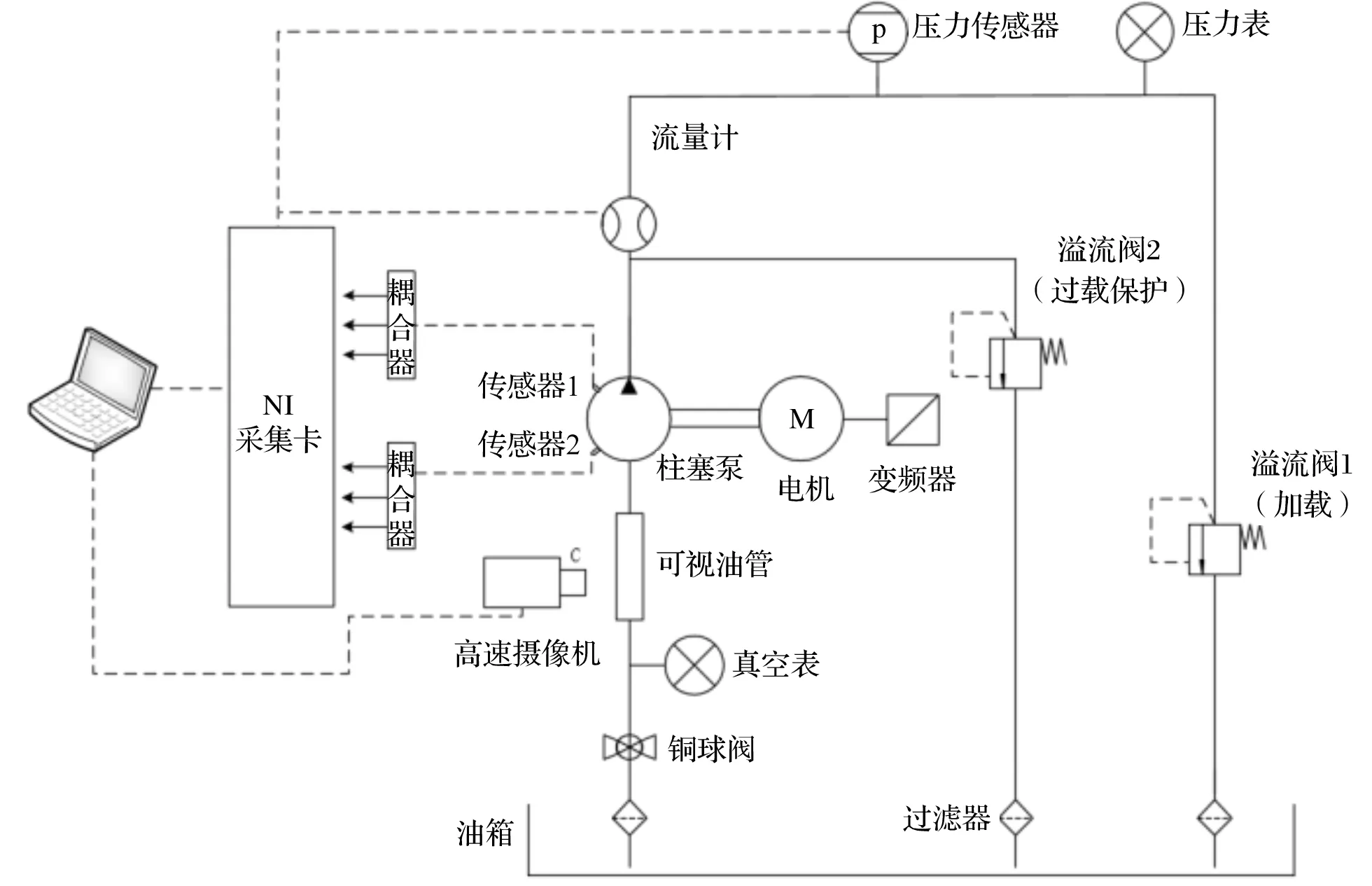
圖3 柱塞泵空化實驗臺原理圖

此外,根據實驗方案,筆者設置了兩種不同的回路負載壓力(即1 200 r/min—10 MPa和1 200 r/min—15 MPa兩種工況)。

在進行實驗采集數據時,在不同的空化狀態下,筆者同步采集了兩種工況下柱塞泵的振動信號、出油口的壓力和流量信號;在進行數據采集時,筆者又將LabVIEW軟件中的采樣頻率設置為45 kHz;此外,每種狀態采集5組數據,每組采樣時間為2 s,共計90 000個數據點。

筆者利用WS(window slicing)方法對各空化運行狀態下采集的柱塞泵原始振動數據進行數據增強。

其中,窗口大小設為1 000,偏移量設置為500。在進行窗口平移的同時,對每個窗口中的1 000個數據點進行minimax歸一化。

最終,每個樣本包含1 000個數據點,每類柱塞泵運行狀態包含895個樣本,空化數據集包含2 685個樣本。

在1 200 r/min—10 MPa工況下,柱塞泵的不同空化狀態時域波形,如圖4所示。

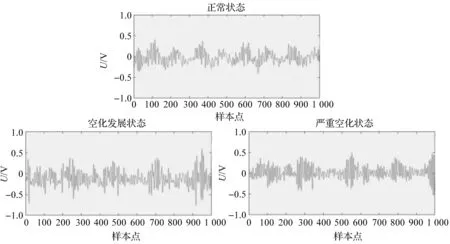
圖4 不同空化狀態原始振動信號

2.3 模型訓練及參數設置

筆者使用交叉熵損失函數來評估模型實際輸出與期望輸出的距離;然后,利用Adam算法不斷優化交叉熵損失函數,以減小兩個分布之間的距離。

此外,在模型的訓練過程中,為減小過擬合,筆者引入了Dropout正則化手段;同時,在每個濾波器層之后,都會進行批標準化處理(batch normalization),以減少參數調節,使網絡能加速收斂,避免過擬合。

在構建模型時,卷積核的數量和大小、雙向長短時記憶層的神經元數、批大小和學習率等參數的選取對模型的訓練速度及最終結果有很大影響。

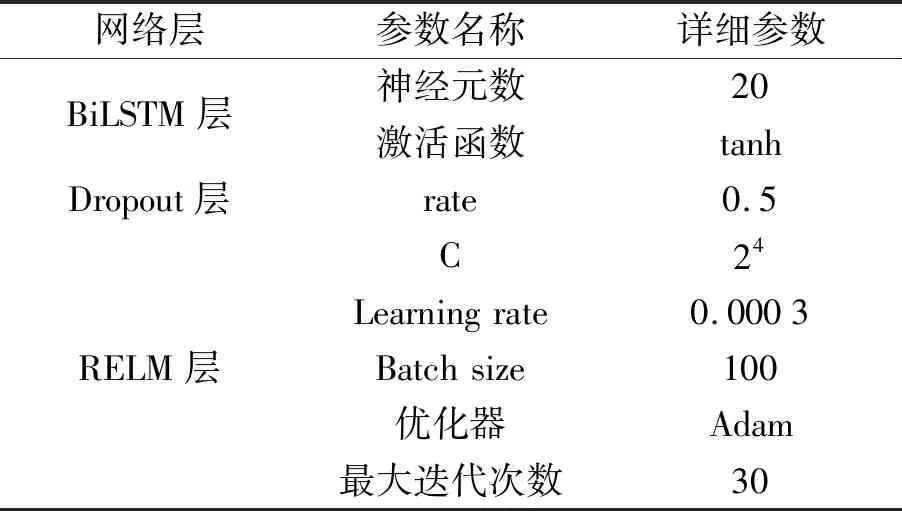
模型的具體參數如表1所示。

表1 模型參數設置

續表

3 實驗及結果分析

3.1 模型比較

為測試CBLRE模型的性能,筆者使用相同的數據集對不同的模型進行測試,并進行相應的微調。模型的參數按照表1進行設置,并訓練10次求其平均值。

不同模型結構的驗證集平均準確率如表2所示。

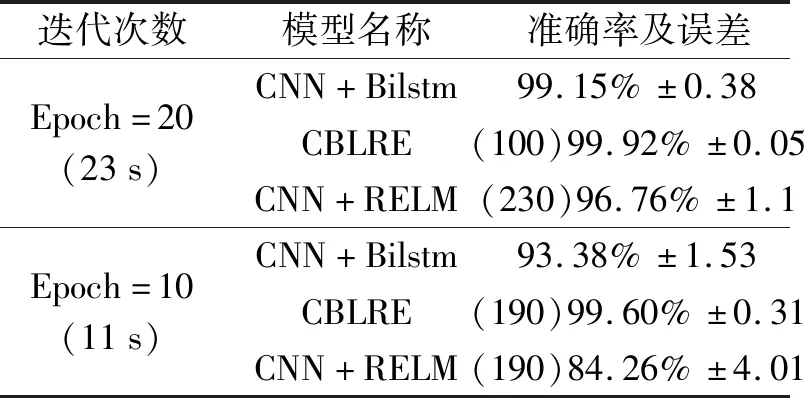
表2 不同模型結構的驗證集平均準確率

從表2中可看出,筆者為了驗證雙向長短時記憶層(Bi-LSTM)是否學習到了特征序列的時間依賴性,在濾波器層后直接利用RELM分類器進行分類,即CNN+RELM,結果發現其精度明顯降低,且模型偏差很大,說明有必要在模型中加入雙向長短時記憶層。

當迭代次數為20時(平均訓練時長為23 s),在雙向長短時記憶層后利用全連接層和SoftMax層進行分類,即CNN+Bilstm,其識別率可以達到99.15%;而利用RELM分類器時,即CBLRE,其識別率可以達到99.90%。其中,全連接層神經元數為30;RELM分類器的隱層神經元個數為100;

當迭代次數為10時,CNN+Bilstm模型的識別率僅為93.38%,但CBLRE模型的識別率仍能達到99.60%。

以上結果表明:在深度學習網絡結構中加入非線性分類器,在保證識別準確率的前提下,可以提前結束迭代,節省其計算成本。

3.2 模型魯棒性分析

考慮到設備在實際使用中負載會發生變化,筆者對10 MPa和15 MPa負載下的柱塞泵空化狀態識別分別進行研究。

由于兩種工況的數據集規模相同,筆者對每個數據集分別進行10次重復實驗,模型迭代次數為10,不同負載下空化狀態的識別率為99.60%和99.32%,分類器的神經元數為190和80,得到的最終結果由混淆矩陣表示。

此外,筆者同時采用兩種負載下的樣本對模型進行訓練和測試,其中,每種負載的樣本各占總樣本數的1/2;數據集的規模與之前相同,模型迭代次數為20,經過10次重復實驗,其精度仍能達到99.03%,神經元數為110。

10 MPa時,由混淆矩陣表示的識別結果如圖5所示。

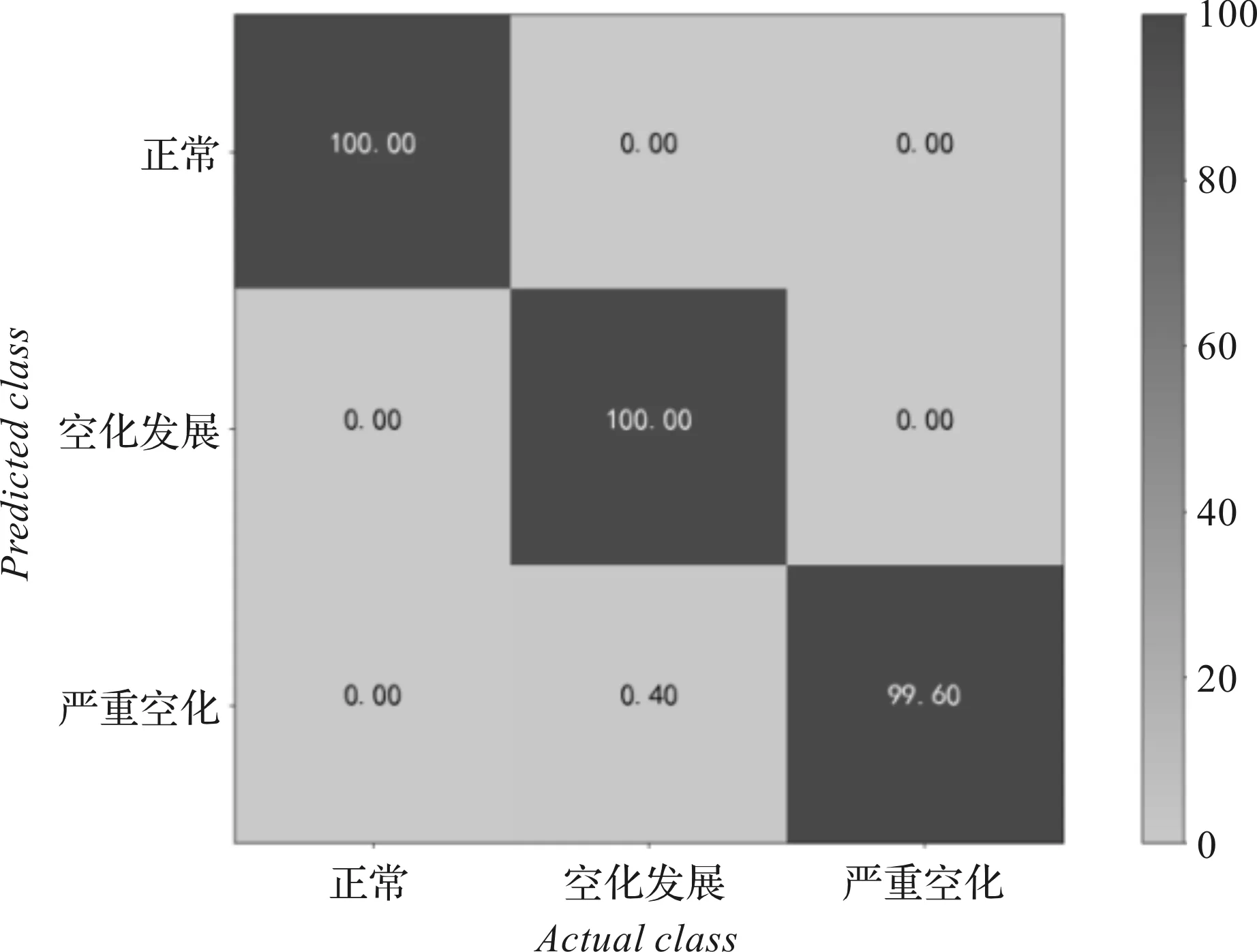
圖5 10 MPa時的識別結果

15 MPa時,由混淆矩陣表示的識別結果如圖6所示。

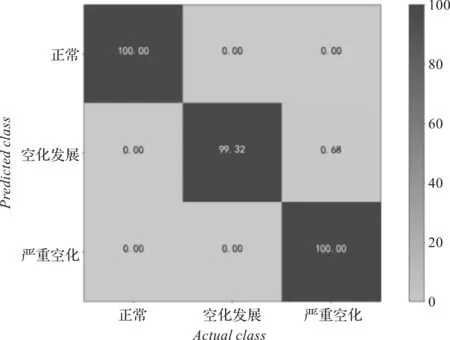
圖6 15 MPa時的識別結果

10 MPa+15 MPa時,由混淆矩陣表示的識別結果如圖7所示。

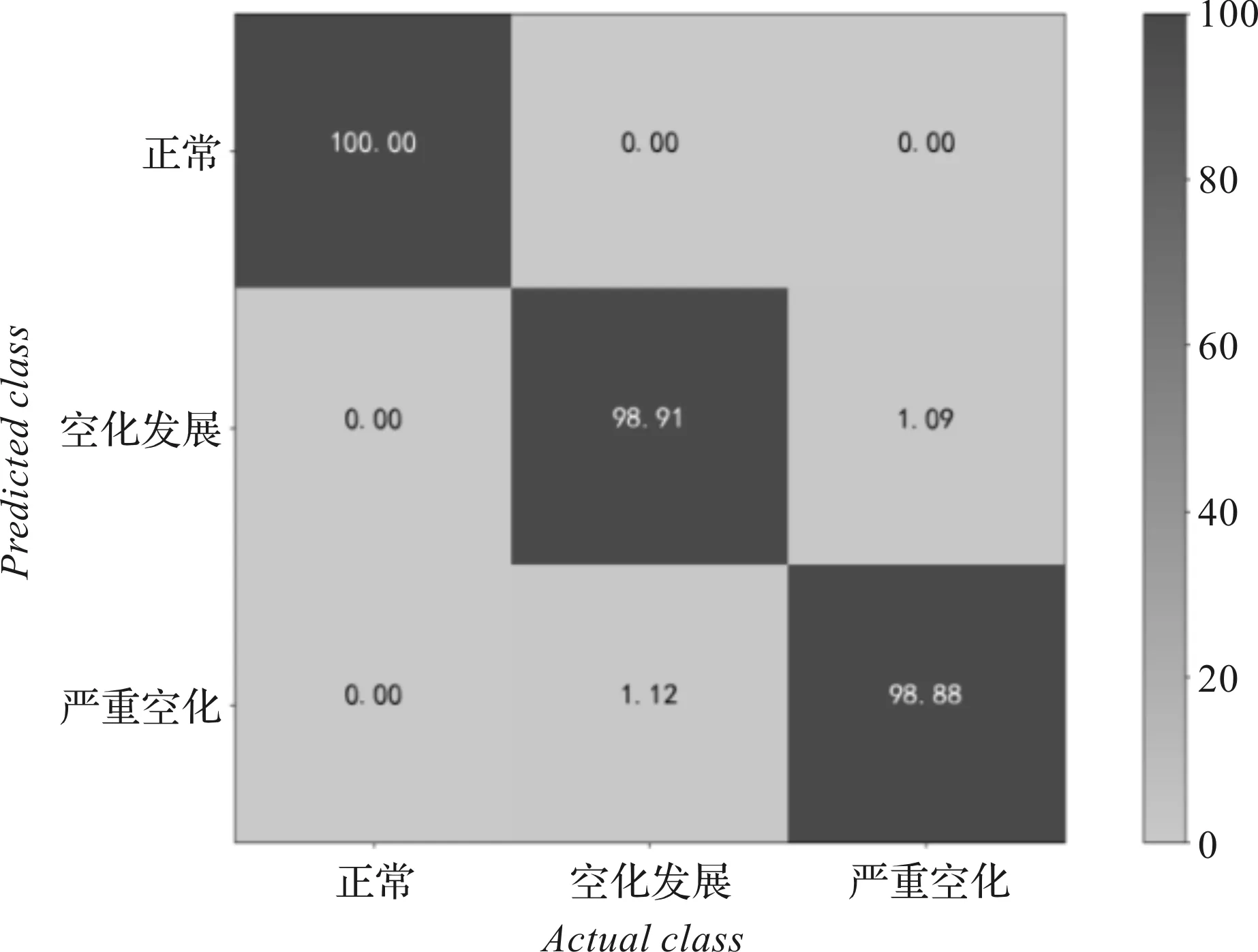
圖7 10 MPa+15 MPa時的識別結果

3.3 空化與其他故障的區分

為驗證該模型是否可以將柱塞泵的空化與其他故障區分開來,筆者將柱塞泵其他典型故障的數據添加標簽,然后將其加入到了空化數據集中,利用上述數據集訓練CBLRE模型,且兩種負載都進行了10次重復實驗,并求其平均值。模型迭代次數為10,兩種負載下柱塞泵故障的識別率為99.49%和99.88%,分類器的神經元數為40和80。

10 MPa時,多種故障的識別率如圖8所示。

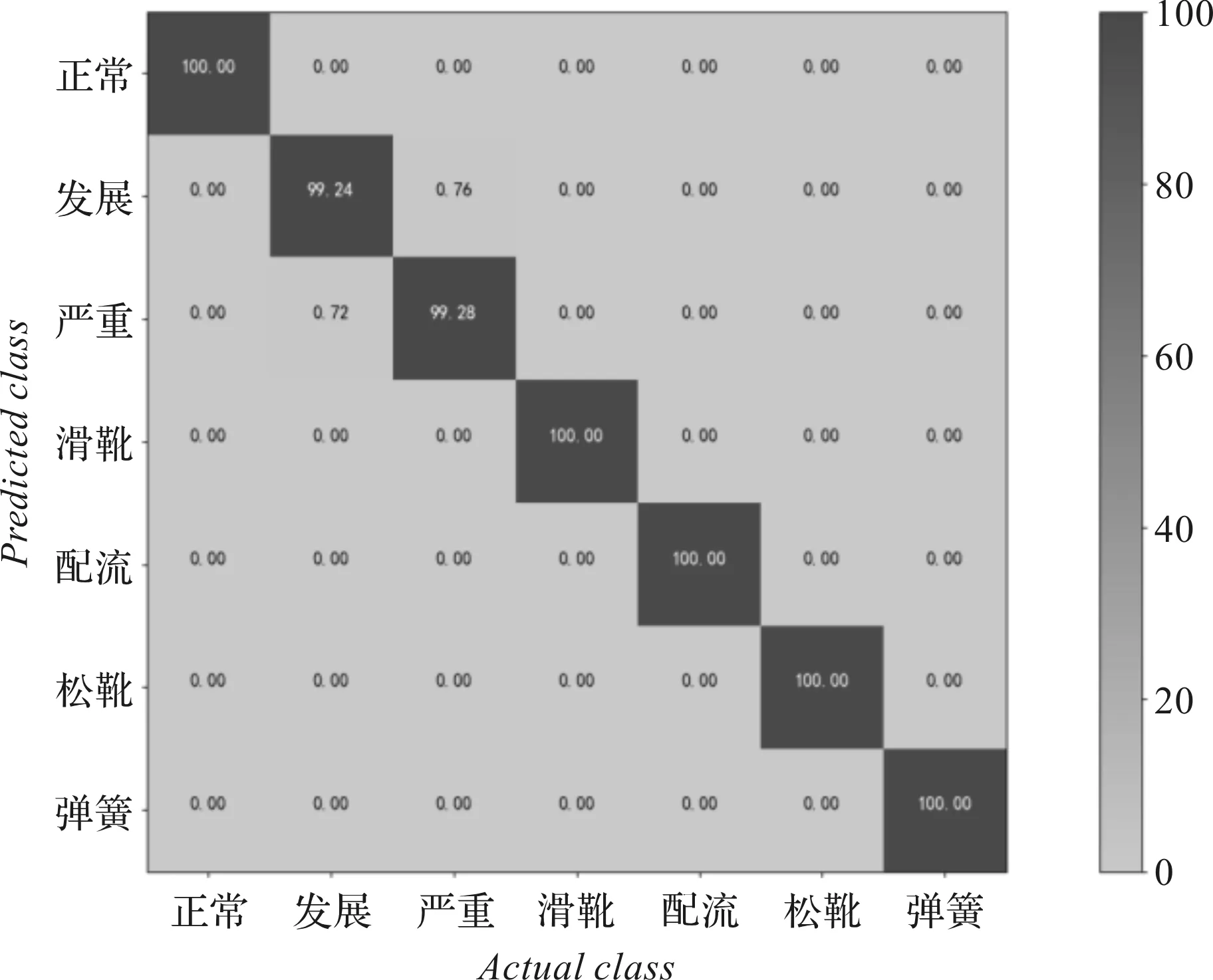
圖8 10 MPa時多種故障的識別率

15 MPa時,多種故障的識別率如圖9所示。

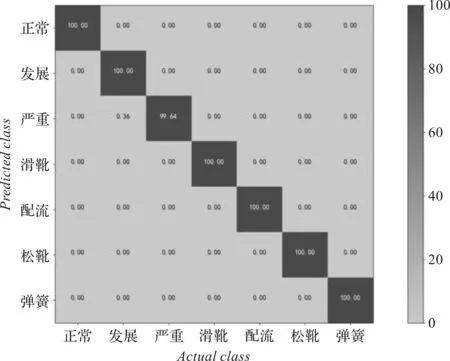
圖9 15 MPa時多種故障的識別率

由圖(8,9)可知:雖然故障的種類有所增多,但模型可以學習的樣本數量也相應增加,所以模型的性能有所提升,可以在花費較少時間的情況下,有效地識別柱塞泵的各種故障。

4 結束語

為了對柱塞泵的空化狀態進行檢測,對柱塞泵進行智能故障診斷,筆者提出了一種基于CBLRE(CNN+BiLSTM+RELM)模型的柱塞泵空化狀態識別方法。

該方法結合了深度學習網絡與非線性分類器的優點,先利用深度學習網絡自動提取一維原始振動信號的特征,然后再學習特征序列的時間依賴性,用非線性分類器進行分類,實現了柱塞泵的空化狀態檢測與智能故障診斷;最后,筆者將CBLRE模型與其他模型進行了對比實驗,分析了該模型在不同工況下的性能。

研究結論如下:

(1)CBLRE模型可以自適應地提取柱塞泵振動信號的特征,且無論是在相同工況還是在混合工況下,對柱塞泵空化狀態的識別率均在99%以上,這表明該模型有很強的魯棒性;

(2)相較于其他模型結構,CBLRE模型結構更為穩定,其訓練時間更短,對空化狀態的識別率更高;

(3)CBLRE模型可以將空化和其他柱塞泵故障有效地區分開,且其識別率同樣在99%以上。

從上述結果可以看出,這種基于CBLRE模型的柱塞泵空化狀態識別方法可以對柱塞泵的空化狀態進行準確識別。

在后續的研究中,筆者將采集空化現象和柱塞泵其他故障耦合發生時的振動信號,并結合故障解耦機理,訓練出一個復合故障診斷模型,以實現對柱塞泵復合故障進行診斷的目的。