鈾材料快中子多重性測量方程推導

黎素芬 李凱樂 張全虎 蔡幸福

(火箭軍工程大學,西安 710025)

隨著國際核裁軍的深入推進,針對核材料的屬性認證愈發受到關注.快中子多重性測量技術作為一種無損檢測技術,采用閃爍體探測器進行測量,在軍控核查體系中發揮著越來越重要的作用.目前對于钚材料的快中子多重性測量方法發展較為成熟,對于鈾材料的快中子多重性分析模型和測量方程還處于發展中.為建立鈾材料的有源快中子多重性測量方程,本文在中子多重性分析方程推導過程的基礎上,根據鈾钚材料二者物理過程的區別,不考慮(α,n)反應,考慮快中子散射串擾的影響,利用概率母函數完成鈾材料快中子多重性測量方程的推導.在此基礎上,為檢驗測量方程的有效性,利用Geant4 搭建一套3×8 的井型探測系統進行模擬測量.通過分析對比耦合系數與增殖系數的擬合函數關系、多重計數率、質量求解偏差,證實了測量方程的可靠性和準確性,對快中子多重性技術的發展具有重要意義.

1 引言

中子多重性(NMC)分析方法作為一種無損檢測手段,能夠實現對密閉容器內放射性物質的定量分析,在深度核裁軍、核材料庫房管理中發揮著重要作用[1].Bohnel[2]于1985 年提出的Bohnel 方法是當前中子多重計數中最基本和最有用的方法之一.為提高探測效率,Bohnel 曾使用負載硼的塑料閃爍體(BC454)/鍺酸鉍(BGO)磷光體檢測器陣列進行了研究[3].隨著美俄等國逐漸限制3He 的對外出口,造成供需不平衡,導致價格的不斷攀升.為尋找有效的替代品,液閃探測器逐漸登上舞臺.基于經典NMC 分析方法發展而來的快中子多重性(FNMC)分析方法,不需要經過高聚合物的慢化過程,能夠克服中子多重性測量過程中的不足,有效保留中子的能量和時間信息,在核材料衡算和屬性認證中發揮著越來越重要的作用[4].中子多重性測量根據有無外部中子源可以分為被動測量和主動測量,如圖1 所示.

圖1 中子多重性測量類型Fig.1.Type of the neutron multiplicity measurement.

被動測量法不需要外部中子源的誘發,主要依托于核材料的自發裂變反應,多用于自發裂變率較高的材料,例如240Pu,238U.針對此類材料的快中子多重性測量方法發展較為成熟,建立了分析模型推導出了快中子多重性測量方程并進行檢驗修正[5].在三階方程的基礎上還推導出了高階測量方程,但由于實際測量偏差較大,應用效果不夠理想[6].對不同豐度、不同封裝材料下的钚材料進行了研究,并提出采用了M,α系數修正的方法縮小測量偏差[7,8].主動測量法通過外部中子源照射核材料進而促使其發生誘發裂變,主要用于誘發裂變率較高的材料,例如235U,239Pu.針對此類材料的快中子多重性測量方法起步較晚,未見公開發表的測量方程.美國密歇根大學Hua 等[9,10]采用有機閃爍體對237Np 進行了快中子多重性測量,但采用的卻是熱中子分析模型.近年來,研究機構加大了對鈾材料的快中子多重性測量方法的重視,對不同質量、密度、豐度的鈾材料以及Am-Li 中子源能譜對測量結果的影響進行了大量研究[11].有研究通過建立鈾材料的數學模型,提出了R=F·P·Q·T的方程形式,但依舊未能提出具體的快中子多重性測量方程,不利用快中子多重性測量的深入研究[12].經典的NMC 方程實現了對樣品參數的求解,但卻不適合于存在散射串擾的快中子多重性測量[13],推導鈾材料的快中子多重性測量方程,對核材料屬性認證具有現實意義.

2 原理模型

參考文獻[14],采用Geant4 搭建一套井型測量系統進行模擬測量研究.該測量系統由24 個液閃探測器組成,共3 層,每層均勻排列分布8 個BC501A 液閃探測器.單個探測器的幾何尺寸為φ120 mm×60 mm,探測器前端面距離探測系統的中心軸20 cm,探測系統的幾何中心設置球形樣品(90%235U 和10%238U),空腔填充空氣.在距離樣品正中心上方10 cm 處放置外部中子源,源強設置為1×104n/s,能量為0.3 MeV,系統布局結構如圖2 所示.

圖2 測量系統模型的(a)剖面圖和(b)俯視圖Fig.2.(a) Sectional view and (b) vertical view of measurement system model.

整個模擬測量過程共分為兩部分,一是利用Geant4 搭建一套模擬探測系統,通過對樣品、探測器、物理過程、測量閾值進行設置,實現對中子裂變及輸運的全過程模擬,生成list-mode 數據文件,記錄下液閃探測器探測到的中子時間信息;二是利用Matlab 構建一個虛擬移位寄存器,通過設置符合門寬、預延遲時間,實現對中子多重計數率的模擬測量.具體原理模型如圖3 所示.

圖3 模擬測量原理模型Fig.3.Model of the simulation measurement.

3 鈾材料快中子多重性測量方程推導

3.1 基本假設

中子輸運是一個極其復雜的過程,在實際的探測中,中子計數會受到一系列因素的影響[15].為降低方程推導的復雜性和可行性,通過對多重性計數影響因素的討論引入基本假設,簡化方程的推導過程,主要包括以下5 點:

1)假設所有被俘獲的中子都會引起誘發裂變;

2)假設中子衰退時間小于符合門寬;

3)假設所有裂變中子從同一點發射出,即點模型假設,保證中子探測器的效率和裂變概率在樣品體積范圍內是不變的;

4)假設每個中子在第1 個探頭中產生信號后都有相同的概率在第2 個探頭中產生信號,但不會產生第3 個信號,即只考慮發生一重散射串擾的情況;

5)假設次級誘發裂變中子與初級裂變中子具有相同能譜,在這個假設下,兩個中子源具有相同的探測效率、裂變概率和誘發裂變多重性.

3.2 推導過程

鈾材料快中子多重性測量方程是在NMC 分析方程的推導過程基礎上,根據物理過程的差異做出相應改變推導而出的,NMC 分析方程的具體推導過程見文獻[16,17].在钚材料的快中子多重性測量方程的推導中,通過建立一系列的基本假設,將未知參數簡化為3 個,即自發裂變率F、樣品增殖系數M和(α,n)反應比例系數α.而在鈾材料多重性分析中通常不考慮(α,n)反應的影響.因此在鈾材料的快中子多重性測量中,樣品特征參數可以簡化為兩個:自發裂變率F、樣品增殖系數M.本文引入概率母函數、階乘矩和總體矩等數學工具推導測量方程,通過對物理過程的分析建立起樣品參數與多重計數率之間的函數關系.

方程從中子產生、輸運、探測、計數等物理過程出發進行推導,根據誘發裂變中子重數分布和中子在樣品內輸運過程中的數目變化,求得一次誘發裂變的樣品發射中子重數分布(即中子出射率),再根據探測器的探測和計數方式推出真符合重數的總體矩rk(F,α,M);另一方面,根據前景計數分布f、背景計數分布b與真符合重數分布r之間的關系,推出由測量計數表示的真符合重數樣本矩rk(f,b).令總體矩與樣本矩相等即可得到參數估計方程,進而得到測量方程.

1)源事件的概率母函數

首先對增殖系數M作如下定義:

其中h′(1) 是每個初級中子所致樣品發射中子數的一階矩.每次發生誘發裂變時發射的中子重數是獨立同分布的非負整值隨機變量,用概率母函數表示為

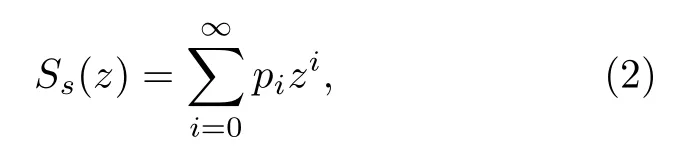
其中pi表示發射i個中子時的概率.一次源事件發射中子數的概率母函數為

根據概率母函數的性質,一次源事件發射中子數的一、二、三、四階矩分別為

2)樣品發射中子數的概率母函數

源事件產生1 個中子,從樣品中發射出來的中子數的概率母函數記為h1(z).源事件產生n個中子,則根據概率母函數的性質,發射中子數的概率母函數為

將樣品中1 個中子發生誘發裂變的概率記為Pif,誘發裂變產生i個中子的概率記為Pifν(i),這i個中子所致樣品發射中子數的概率母函數也為hi(z).

一次誘發裂變產生中子數的概率母函數為

中子在樣品中有可能被吸收,也可能未被吸收,未被吸收概率為1-Pif.假設中子在樣品中只要被吸收都會誘發裂變,忽略中子在樣品中被吸收而沒有誘發裂變的可能性,根據概率母函數的性質有

為書寫方便,后面統一用h(z)代替h1(z),即

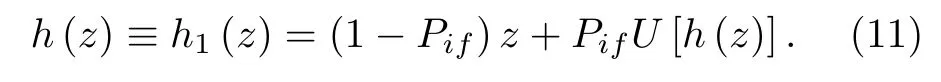
(11)式給出了源事件發射(產生)1 個中子時,樣品發射中子數概率母函數h(z)與誘發裂變概率Pif和誘發裂變發射中子數U(z)之間的關系.考慮源事件發射(產生)中子數分布,根據概率母函數的性質,一次源事件中樣品發射的中子數概率母函數為

3)源事件產生的泄漏中子數的階乘矩

根據概率母函數的性質,一次源事件對應的樣品發射中子數的一、二、三階階乘矩為

對(11)式求z=1 處的導數,得

考慮到二次誘發裂變中子階乘矩可由核數據計算得到,用vi1代替U′(1),后面使用vi2,vi3,vi4代替U′′(1),U′′′(1),U′′′′(1).h′(1)是每個源中子在輸運過程中的增殖期望,記為M,則M為

求z=1 處的二階導數,可獲得中子增殖的二階矩、三階矩和四階矩:

4)真符合重數的總體矩

假定同屬一個源事件的中子中有n個被探測到,在其中隨機選取一個作為觸發信號,下面推導這個觸發信號的真符合計數重數的概率分布p(i|n).

假設源事件發生在t=0 時刻,探測到的中子信號時間分布為f(t),計數門寬為G,預延遲為PD.在(t,t+dt)內能夠探測到1 個中子的概率為

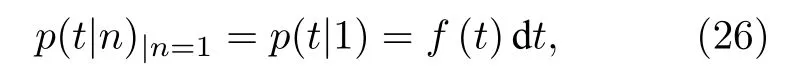
在(t,t+dt)內能夠探測到n個中子的概率為

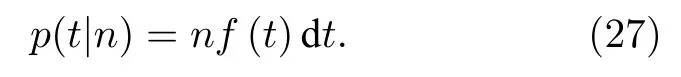
以其作為觸發信號的計數門為從t+PD時刻到t+PD+G時刻,其余n?1 個中子信號中的任意1 個處于此計數門中(記為事件A,對此次觸發的計數重數產生貢獻)的概率為

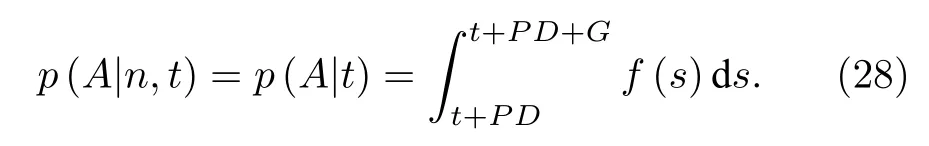
所以(t,t+dt)內探測到1 個中子,并且余下的n?1個中子中在計數門中有i個的可能性為

在整個時間范圍對t做積分,即得到隨機選取n個信號中的一個作為觸發信號,所記重數為i(計數門中有i個中子信號)的概率為

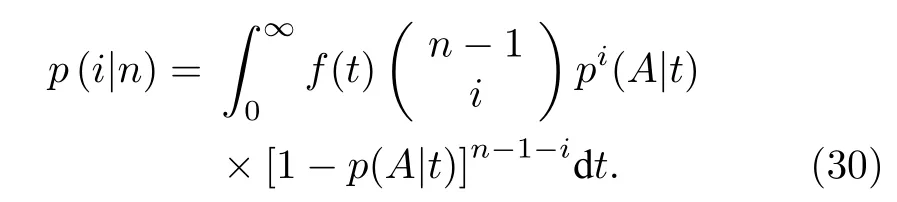
每個中子被探測器探測到的概率稱為探測器的探測效率,記為ε,則一個樣品發射中子產生信號數的概率母函數為(考慮散射串擾,k為散射串擾因子):

一個源事件產生信號數的概率母函數為

一個初級時間探測中子重數的前三階階乘矩為

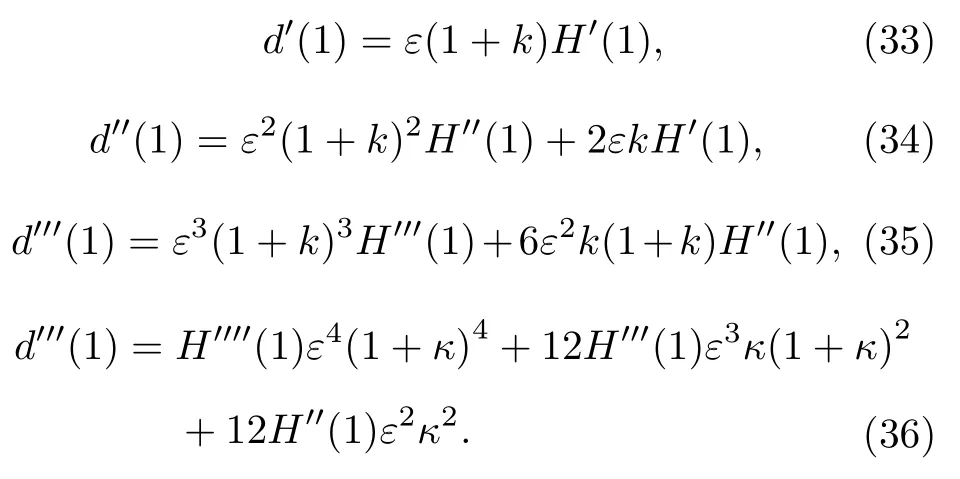
記一次源事件探測到的中子數為n的可能性為D(n),則對于每個探測到的中子都會觸發一次計數,則某一個觸發中子屬于探測到n個中子的源事件的可能性為

所以,某次計數重數為i的概率為

一、二、三階矩為

fd,ft,fq分別是探測器的二重、三重和四重符合門因子:

根據基本假設的第5 條,探測到的中子信號時間分布為

所以

在快中子探測中由于中子衰減時間不滿足指數關系,所以fd=ft=fq=1.

5)測量計數與真符合重數的關系

探測到的中子既包含源事件誘發裂變產生的中子,又包含與源事件無關的本底中子.前景計數器以探測到的中子為觸發,總觸發率為

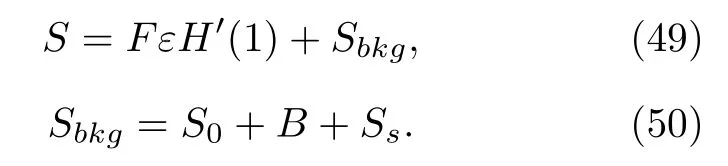
前景重數的階乘矩為

其中bk為本底中子觸發重數,即偶然符合重數,與背景重數分布相同.gk為源事件中子觸發重數,包含真符合重數rk與偶然符合重數bk:

對于k=1,2,3 使用fk,bk的顯式表達,可以獲得真符合重數的一、二階矩:

令真符合重數的總體矩((39)—(41)式)與樣本矩((54)—(56)式)相等得到

(57)—(60)式的左端就是需要的一、二、三、四重記數Single,Double,Tribple 和Quarts,為了書寫方便,簡單記為S,D,T,Q.結合(22)—(25)式可得

式中,vs1,vs2,vs3,vs4分別是外部中子源誘發裂變發射中子數分布的一、二、三、四階階乘矩,vi1,vi2,vi3,vi4分別是次級誘發裂變發射中子數分布的一、二、三、四階階乘矩,ε是探測器的探測效率,fd,ft,fq分別是探測器二重、三重、四重符合門因子.由于主動中子測量是利用外部中子誘發鈾材料裂變,所以測得的誘發裂變率與鈾材料質量、外部中子源強度以及耦合系數有關,如下式所示:

耦合系數C是有源多重性測量過程中的關鍵參數,與樣品的幾何結構、密度、材料組成等有關,難以通過理論計算的方法求出.Krick 研究團隊[3]揭示了耦合系數和增殖系數之間的經驗關系式:

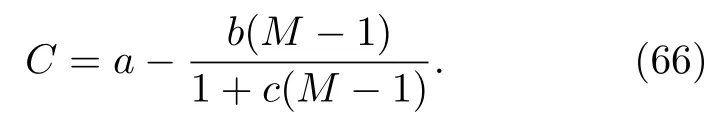
方程的求解過程為利用測得的二重計數率D和三重計數率T迭代消元求得增殖系數M,再將M代入方程求解出誘發裂變率F,將已知的參數m,F,Y代入公式求出耦合系數C,通過一系列的C和M擬合得到刻度系數a,b,c,進而得到耦合系數與增殖系數的具體表達式.根據確定好的耦合-增殖關系曲線計算出耦合系數的值,再由(65)式解出235U 的有效質量.

4 驗證及分析

為對上述推導鈾材料快中子多重性測量方程進行驗證,利用上述搭建的探測系統進行模擬測量.設置一系列質量的樣品,測量結果如圖4所示.

圖4 中子多重計數率的測量結果與文獻[14]相似,基本維持在同一量級內.增殖系數分布見圖5,增殖系數會隨著樣品質量的增大而增大,與文獻[11]中的擬合曲線基本吻合,說明了測量結果的準確性.

圖4 中子多重計數率分布圖Fig.4.Distribution of the neutron multiplicity counting rates.

圖5 增殖系數分布圖Fig.5.Distribution of the multiplication coefficient.

通過測得的裂變率F、模擬測量時預設的樣品質量以及中子源強度Y可以發解出對應的耦合系數C.將耦合系數和增殖系數進行擬合(見圖6),得到擬合方程為C=a/(M+b),系數a=0.6173,b=–1.196,擬合優度達0.9923,反映了擬合曲線的高度吻合.對耦合系數和增殖系數之間的經驗公式(66)進行化簡,得到如下公式:

圖6 耦合系數 C 與增殖系數 M 擬合函數Fig.6.Fitting function of the coupling coefficient C and the multiplication coefficient M.

通過對化簡方程與擬合方程進行比較,發現二者的函數形式高度相似,說明了擬合方程的可靠性.將部分測量數據代入擬合方程進行檢驗,通過多重計數率的迭代消元,得到增殖系數M,代入擬合方程求得耦合系數C,利用m,F,Y,C的函數關系解得樣品質量m,與理論值對比,得到測量偏差如圖7 所示.

圖7 求解偏差分布圖Fig.7.Solution deviation distribution.

在2 kg 范圍內,樣品的質量求解偏差絕大多數保持在20%以內,且小質量樣品測量偏差偏小,隨著樣品質量的增大,求解偏差呈現擴大趨勢.分析原因主要有兩部分:一是多重性測量方程是建立在點模型的基礎上的,而在實際測量中放射源往往是以體源的形式呈現的.二是耦合系數與增殖系數擬合曲線的偏差也會對測量結果造成一定的影響.

5 總結

本文在NMC 分析方程的推導基礎上,采用概率母函數完成對鈾材料快中子多重性測量方程進行推導.根據鈾钚材料物理過程的差異,在鈾材料的快中子多重性測量中忽略了(α,n)反應系數α,并引入了常數k修正快中子的散射串擾影響,推導出了鈾材料快中子多重性測量方程.

為檢驗方程的準確性,分別利用Geant4 和Matlab 實現中子探測和中子計數的模擬過程,得到不同質量情況下樣品特征參數.對耦合系數與增殖系數進行擬合,得到方程C=a/(M+b),與經驗方程C=a?高度吻合.將擬合方程代入計算,得到2 kg 范圍內質量求解偏差小于20%,證實了測量方程的可靠性.此項研究建立了鈾材料快中子多重性測量方程,實現了鈾材料的質量屬性認證,拓展了快中子多重性的應用范圍,對軍控核查技術的發展具有重要意義.