承壓破碎煤體空隙率分形模型及試驗研究
徐義洋,褚廷湘,馮學文,代文程
(1. 北京中煤礦山工程有限公司,北京 100013;2. 華北科技學院 安全監管學院,河北 三河 065201;3. 中國礦業大學(北京) 機電與信息工程學院,北京 100083; 4. 安徽省皖北煤電集團臨汾天煜恒昇煤業有限責任公司,山西 臨汾 041204)
井工煤礦其煤自燃主要發生在采空區、破裂煤柱等地點,其中以采空區的發火次數最多、造成的損失也最嚴重。因此采空區自然發火的研究,一直都是礦井火災防治領域所關注的重點方向。在煤自燃發生及發展過程中,涉及到流固介質之間的傳質及傳熱過程,而在這一過程中,空隙率對煤自燃的發生及發展進程具有內在的作用。王繼仁等應用分形理論,分析了氧氣在散體煤中的擴散問題,建立了氧氣在散體煤中的分形擴散方程和散體煤顆粒分形表面氧氣吸附速率方程。高建良和王海生根據多孔介質滲流理論,分別模擬了采空區滲透率為均勻、分段均勻和連續性分布情況下的采空區漏風流場,發現漏風量、漏風風速分布和自燃三帶的位置和寬度有很大差別。李樹剛和錢鳴高通過理論分析和現場觀測,分析了綜放采空區垮落巖體碎脹特性與采空區流態的影響。楊永良等利用數值模擬及實測的方法,分析了煤巖垮落規律與采空區自燃規律之間的關系。自分形理論提出以來,在礦業領域此理論也得到了廣泛使用。謝和平等運用分形理論研究了巖石的斷裂和破碎問題,及綜放工作面巷道裂隙發育情況。李宏艷等通過采動條件下裂隙場演化實驗室相似模擬實驗,利用分形理論定量描述了裂隙時空的演化規律。鄭克洪等根據分形理論建立了煤矸破碎粒度分布的分形表達式。姜秀民等根據實驗數據研究了煤粉顆粒的分形特征。KATZ等把分形幾何理論用于分析多孔介質內部的孔隙結構。他們的研究表明:多孔介質的孔隙空間和孔隙界面都具有分形特征,可以用分形維數來預測多孔介質的孔隙度。以上研究可以看出不論是從宏觀巖石破斷、覆巖裂隙、煤矸破碎,還是在微觀尺度分形理論描述空隙率也是可行的。
上述研究對描述采空區破碎煤巖空隙率提供了途徑,但是由于采空區垮落的不規則性及采空區內部的不可接近性,造成對采空區自燃環境的識別比較局限。而遺煤自燃的發生卻與其所在的堆積狀態及環境條件息息相關,在自燃發生及發展過程中滲流場、氧濃度場、溫度場之間的相互作用、相互聯系,這其中最關鍵的問題在于采空區破碎遺煤的堆積結構的復雜性,此外進行全尺度的研究的設備手段還不能實現。因此,筆者基于煤自燃角度及采空區遺煤垮落特征,剔除矸石堆積部分,只關注垮落帶內破碎遺煤承壓下空隙率演變,結合分形理論,建立了顆粒煤堆積體承壓下的空隙率模型,并對加載應力條件下顆粒煤的空隙率演化進行嘗試。
1 空隙率對煤自燃進程影響分析
采空區遺煤自燃與覆巖垮落關系密切,煤巖垮落狀態決定了采空區破碎遺煤的堆積狀態,而遺煤堆積空間結構及變化,直接影響煤的蓄熱環境和采空區的漏風狀態及氧氣分布。
1.1 覆巖垮落與堆積
據巖層的移動特征及礦壓理論將煤層的上覆巖層在垂直方向上分為垮落帶、裂隙帶、彎曲下沉帶。工作面后方的采空區,初次來壓之前只有采空卸荷區,初次來壓之后開始逐漸形成應力升高區和應力恢復區,但初次來壓后的工作面與應力升高區之間仍存在采空卸荷區。采空區覆巖垮落與應力分布如圖1所示,其中,為工作面走向卸壓區寬度,為工作面走向應力集中區寬度,為采空區走向應力逐漸回復長度,m。在緊靠工作面后方,受支架及上部未完全破斷的巖梁掩護,未受到基本頂來壓的應力影響,浮煤及矸石處于自然堆積狀態,稱之為自然堆積區;隨著采空區應力逐漸恢復,浮煤及矸石不再成自然狀態堆積,在壓應力作用下浮煤及矸石進一步破碎,密實度增加,稱為破碎堆積區;當隨著采空區深度的增加,采空區底板應力恢復到原巖應力水平而重新壓實區,密實度最大,稱為壓實區。
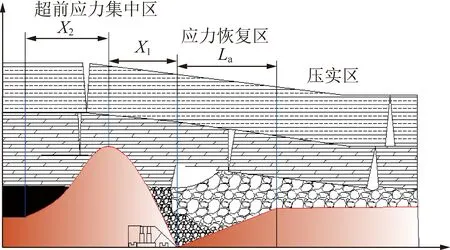
圖1 采空區覆巖垮落及應力分布示意Fig.1 Diagram of the strata caving and stress distribution in goaf
采空區遺煤先后經歷卸壓應力區、應力恢復區及原巖應力區3個階段,在每個階段遺煤所承載的應力不同,致使遺煤堆積結構發生變化,進而影響遺煤堆積區域的空隙率。從煤自燃角度分析,進而影響到采空區的漏風狀態、漏風強度及溫度場環境,即影響采空區遺煤的自然發火的進程。文獻[15]在實驗室內通過對散體煤進行加載實驗,得到了軸向應力與碎脹系數的關系,發現隨著軸向應力增加,碎脹系數降低,逐漸趨于壓實,進而改變破碎煤體的空隙率。所以如何確定采空區承壓破碎煤體在應力變化條件下的空隙率響應特征,對研究采空區煤自燃的發生顯得尤為重要。
采空區覆巖應力對空隙率的影響是間接的,是通過影響采空區煤巖的碎脹系數來影響空隙率的,空隙率與碎脹系數存在以下關系:
=1-1
(1)
由式(1)可以看出,空隙率與碎脹系數成正比關系:碎脹系數越大,空隙率亦越大。
1.2 空隙率與煤自燃關系
對于一個特定的綜放工作面,其通風方式、供風量、風壓分布等基本確定,影響漏風強度的主要因素是松散煤體的空隙率。漏風強度是風壓梯度、空隙率的函數。
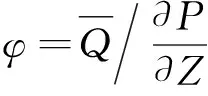
(2)
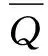
由式(2)可以看出,當漏風通道兩端壓差一定情況下,空隙率越大,漏風量越大,空隙率影響漏風區域的漏風強度。在采空區漏風強度一定的情況下,采空區遺煤堆積環境的氧氣體積分數的分布與空隙率分布有關。
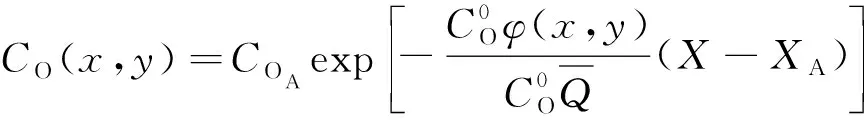
(3)
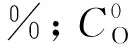
由式(3)可以看出,采空區某點的氧氣體積分數與空隙率的分布有關。
根據能量守恒定律,考慮氣固兩相時,采空區遺煤的溫度方程為
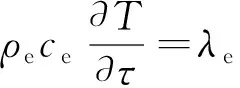
(4)
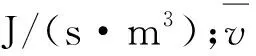
由式(4)可以看出,采空區遺煤堆積空間的空隙率對溫度場的演化具有重要影響。
綜上,可見空隙率對采空區漏風強度、氧氣體積分數的分布、溫度場的分布影響較大,因此基于采空區應力恢復特征,如何定量描述其在應力擾動下的空隙率計算模型,對煤自燃研究來說具有一定的意義。
2 承壓破碎遺煤的分型模型
采空區遺煤堆積空間四周受力,軸向覆巖應力作用為主動應力,同時由于遺煤散體的變形、滑動受兩側煤壁、老開切眼及支架的束縛限制,宏觀表現為以軸向壓實為主,四周相對位移固定的受力狀態。在承壓破碎散體滲透性方面劉衛群、李順才等研究了不同破碎程度下壓實的滲透系數變化規律,指出破碎巖石的滲透性不僅和外載水平及初始孔隙度有關,還與碎石的粒徑、顆粒的排列方式以等有關。PAPPAS和MARK通過20組單軸壓縮實驗,詳細研究了采空區垮落材料的力學性質,通過應力-應變關系,獲得了有關巖石的力學參數及散體破斷特征。梁軍等采用大型壓縮儀進行了堆石蠕變試驗和顆粒破碎測試,指出堆石破碎有主壓縮破碎和蠕變破碎2類,其中蠕變破碎是堆石料骨架應力的重新分布導致粗大顆粒棱角或者軟弱顆粒發生破碎、細化,顆粒排列進一步調整,如圖2所示。
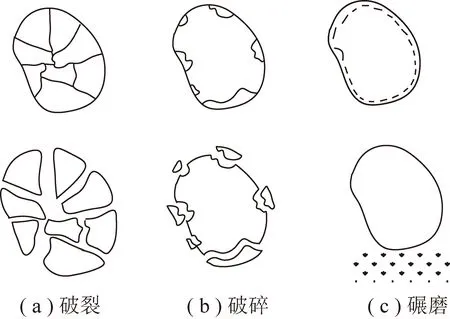
圖2 顆粒破碎類型Fig.2 Particle breakage types
采空區遺煤依次經歷應力三區時,會再次發生破碎,遺煤顆粒破碎在覆巖荷載作用下產生結構的破裂或破損,進而影響其堆積結構與狀態。
2.1 遺煤堆積空隙率分形模型
TYLER等提出了質量和孔徑關系的標準化方程,且通過假設不同土壤粒級具有相同密度的條件,建立了土壤粒徑分布分形維數的質量分布模型。由于采空區遺煤粒徑、形狀不一,根據TYLER的研究結果,可以通過不同直徑的篩子篩分試樣,通過篩下試樣的質量和總試樣的質量建立函數關系,分析遺煤粒度的分布。
設()為篩下試樣質量,()為篩上試樣質量,為試樣總質量,定義關聯函數()為
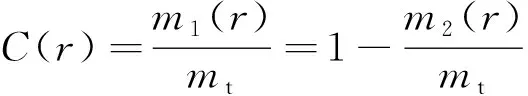
(5)
在三維空間中,大于某一粒度的粗粒顆粒所構成的體積為,則有
=[1-()3-]
(6)
式中,為破碎分形維數;,均為常數,與遺煤顆粒的大小、形狀有關。
假定遺煤顆粒具有相同的密度,則大于某一粒徑的遺煤質量為
()=[1-()3-]
(7)
若令=0,可得到試樣的總質量;若令等于試樣中的最大粒徑,則有()=0,代入式(7)可得=,則可得到遺煤顆粒質量與粒徑之間的分形關系:
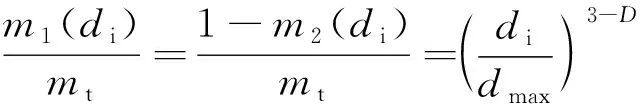
(8)
對式(8)兩邊取對數,則有
ln[()]=(3-)ln()
(9)
通過物理篩分、稱重統計,可得到()的統計值,并依據線性回歸求得直線部分的斜率,即(3-),進而得到遺煤破碎分形維數。
采空區垮落遺煤空隙率為破碎遺煤間的空隙體積與整個垮落堆積體體積之比,設垮落遺煤的顆粒尺寸為,根據密度定義,則有
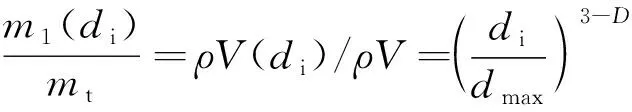
(10)
其中,()為顆粒特征尺寸小于的遺煤分形體積,m;為垮落巖體總體積,m,為破碎煤體密度,kg/m。則對于粒徑小于部分遺煤堆積體積為
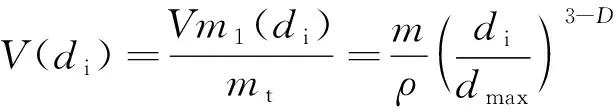
(11)
則,粒徑處于區間(,+d)內的堆積體積為
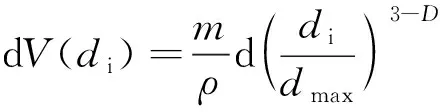
(12)
則,垮落遺煤的分形總體積為
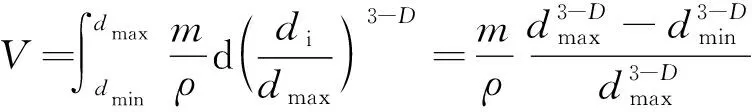
(13)
則有
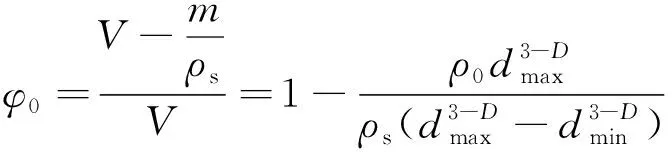
(14)
式中,為垮落遺煤自然碎脹空隙率;,分別為最小及最大顆粒粒徑;為煤的質量;為自然碎脹遺煤密度;為煤層的密度。
2.2 承壓破碎煤體空隙率演變模型
采空區遺煤堆以軸向覆巖應力作用為主動應力,同時由于遺煤散體的變形、滑動受兩側煤壁、開切眼及支架的束縛限制,宏觀表現為以軸向壓實為主,因此可以通過側限壓實實驗,輔助應力-應變關系,得到承壓破碎遺煤的視密度與真密度之間的關系。
軸向應變為
=Δ
(15)
式中,Δ為壓縮變形的煤體高度;為壓縮變形后煤體高度。
假設在側限壓實實驗過程中完整煤樣初始質量為,初始碎脹密度為,自然碎脹堆積裝置內煤樣高度為;承載破碎煤體的密度為,承壓過程中應變為。則承壓后煤樣在不同應力狀態下的高度=(1-),破碎煤體承壓過程中,不斷被壓實,空隙體積隨壓實程度不斷減小,由質量守恒得
=1(1-)
(16)
根據空隙率定義,則承壓破碎煤體的空隙率,可表達為
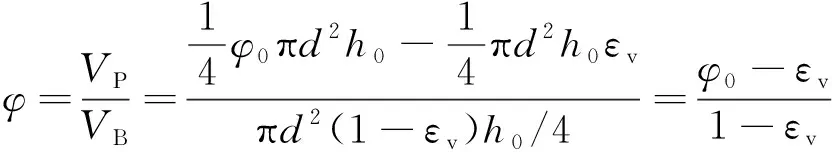
(17)
式中,為顆粒堆積體的空隙體積,m;為顆粒堆積體表觀體積,m。
式(17)有效使用,需滿足:≤,理論上,數值上當=時,煤樣完全被壓實,無任何空隙。
在壓實過程中應力-應變的關系可表達為
=e
(18)
式中,為軸向壓應力;,為壓實回歸系數。
承壓破碎遺煤的空隙率分型模型為
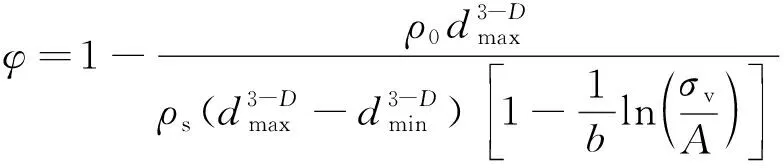
(19)
3 承壓破碎煤體空隙率實驗
3.1 實驗煤樣及方法
所選煤樣來自山西恒昇煤業9106工作面,在該工作面傾向支架后部3個不同位置取樣,選取15 mm以下粒徑的混合煤樣作為試驗煤樣,經自然風干后,進行篩分,確定了自然碎脹區遺煤15 mm以下遺煤堆積體的級配的構成,見表1,其中為顆粒粒徑。

表1 初始各粒徑組質量
其中相同位置煤樣各準備2份分別標記為A,B,C,A,B,C,保持級配相同,一份用于應力應變測試,一份用于特定軸向加載應力下的分形維數確定。
利用實驗室內自主設計的承壓破碎遺煤滲透率演化及自燃測試裝置,如圖3所示。通過此裝置,可對采空區篩選的煤樣開展軸向加載實驗,通過設定不同的軸向加載強度,通過重新篩分,可確定加載后煤樣的級配構成及承壓破碎煤樣的空隙率。

圖3 承壓破碎煤體空隙率測試實驗裝置Fig.3 Porosity test device of the compacted broken coal
3.2 原始煤樣分形維數確定
結合表1,對煤樣粒徑與對應篩下質量比,通過對數取值,然后線性回歸,根據擬合曲線斜率,通過式(9)可回歸得到原始煤樣的破碎分形維數,如圖4所示,其中,為粒徑以下的煤樣質量。通過對原始煤樣的級配篩分及分形維數回歸,利用空隙率分形模型式(14),得到了自然堆積狀態下的A,B,C煤樣的空隙率(表2)。發現利用分形模型計算得到的空隙率與空隙率定義計算出的空隙率誤差在0.045~0.086,空隙率分形模型可用于采空區遺煤孔隙率計算。
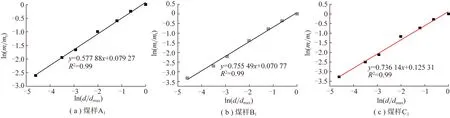
圖4 原始煤樣ln(di/dmax)與ln(mi/mt)回歸Fig.4 Regression curves of the initial coal sample between ln(di/dmax)andln(mi/mt)

表2 原始煤樣分形維數與空隙率
3.3 承壓破碎煤體的分形維數
分別對煤樣A,B,C進行了承壓實驗,通過回歸分析確定了3個煤樣的應力-應變關系,見表3。
由表3可知破碎煤體應力-應變符合指數關系。隨著應力增加,破碎煤樣的應變逐漸增加,即煤樣逐漸被壓實,結合圖1可知在采空區橫三區內,隨著采空區應力逐漸恢復,采空區遺煤堆積體逐漸被壓實。

表3 煤樣承壓應力應變擬合關系
對不同加載應力狀態下的破碎煤樣再次篩分,通過分形理論可得到破碎煤樣的承壓破碎分形維數。
分別測試了煤樣A,B,C在加載8,12及15 MPa后煤樣承載破碎后的級配情況,并對其回歸,得到加載后A,B,C的破碎分形維數,如圖5所示。發現承壓破碎煤體分形維數增大則說明受載煤樣更加破碎,在應力加載狀態下其空隙率逐漸減小。
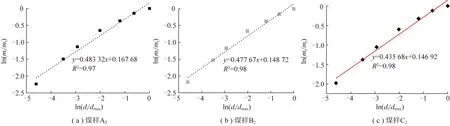
圖5 承壓破碎后煤樣ln(di/dmax)與ln(mi/mt)回歸Fig.5 Regression curves after compacted between ln(di/dmax)andln(mi/mt)
3.4 模型與實驗結果對比
通過對煤樣A,B,C的軸向加載實驗,根據其煤樣質量、煤樣真密度、壓實位移,可得到不同應力狀態下的實驗空隙率;通過表2,4的實驗數據,根據式(19),可確定其分形理論空隙率,見表5。
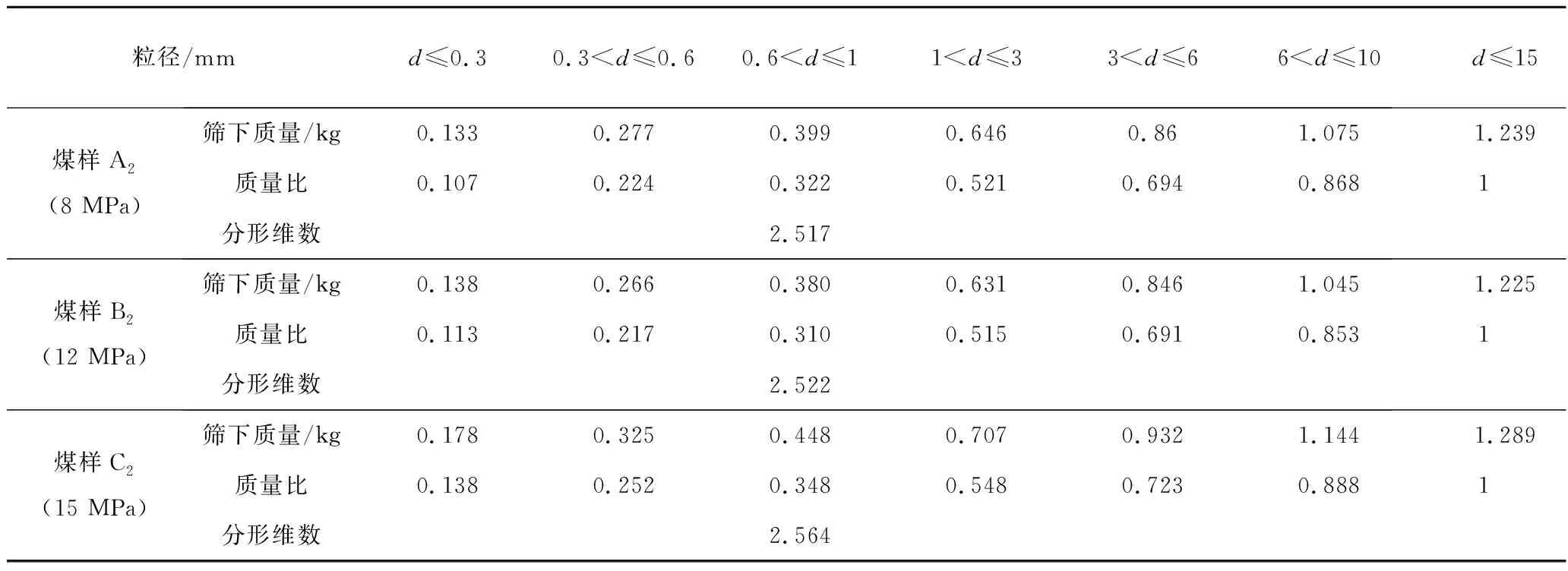
表4 軸向加載后級配及分形維數

表5 承壓煤樣分形空隙率計算結果
經實驗測試及理論計算,得到了煤樣A,B,C分別在加載8,12,15 MPa下的空隙率,通過2者比較,3個煤樣的誤差分別為0.106,0.028,0.062,說明通過承壓破碎遺煤的空隙率分形模型是可以用于預測不同應力狀態下的空隙率變化。
3.5 承壓破碎煤體空隙率預測方法
以B煤樣的應力應變曲線為例,結合承壓破碎遺煤空隙率分形模型,可對不同應力狀態下的破碎煤體空隙率演化進行預測,(式(20))。
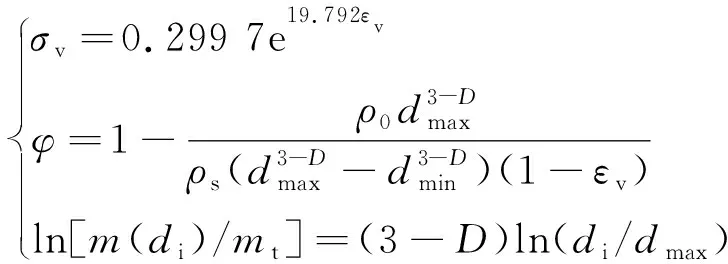
(20)
承壓破碎煤體空隙率預測方法可簡述為:首先獲得其應力-應變曲線,然后根據煤樣的級配構成確定其破碎分形維數后,根據所建立的承壓破碎煤體空隙率分形模型可對其預測。
4 結 論
(1)以空隙率對煤自燃影響為切入點,分析了采空區空隙率對煤自燃發生中的漏風強度、氧氣體積分數分布、蓄熱環境的影響,明確了空隙率變化對采空區煤自燃的影響作用。
(2)結合采空區應力恢復及承壓破碎煤體壓實特征,通過引入分形理論,建立了承壓破碎煤體空隙率分形模型。
(3)通過承壓破碎煤體壓實實驗,明確了壓實前后分形維數的變化,基于實驗數據與推到模型進行了驗證,實驗結果與理論計算結果誤差不大,所建立的模型具有一定的可靠性。通過該研究,為后續研究恒昇煤業采空區漏風、煤自燃氧化區域及瓦斯運移提供了理論指導。
(4)因受限于采空區破碎煤巖全尺度樣本索取困難,本文僅以小樣本尺度煤樣為對象進行了研究,這對于研究采空應力恢復狀態下的空隙率演化提供了一種新思路。

