基于焦面復制方法的自適應光學系統靜態像差校正技術

張天宇，王 鋼，張 熙，竇江培

（1.中國科學院 國家天文臺 南京天文光學技術研究所,南京 210042；2.中國科學院 天文光學技術重點實驗室（南京天文光學技術研究所）,南京 210042；3.中國科學院大學,北京 100049）

1 引言

隨著科學技術的發展，自適應光學已經被廣泛應用于生物、醫學、通信和天文等領域。在天文領域，自適應光學系統通常用于校正大氣湍流引入的波前畸變，獲得接近衍射極限的成像[1-9]。

1994 年，Angel[10]首次提出利用自適應光學技術對系外行星進行直接成像，同時提出了超級自適應光學（Extreme Adaptive Optics，ExAO）的概念。由于系外行星與主星的對比度相差懸殊，其對比度通常在10?6～10?10量級，且行星與恒星的角距離通常為幾個～十幾個λ/D。為了提高成像對比度，ExAO 被應用于在小視場內獲得高成像質量，其校正后的斯特列爾比通常優于0.9，甚至更高；同時可以配合星冕儀進一步抑制望遠鏡孔徑衍射引入的散斑噪聲，進而極大地提高成像對比度[11-12]。

自適應光學系統由共光路的像差校正子系統，非共光路的波前檢測子系統和成像子系統構成。研究表明波前檢測子系統與成像子系統之間的相對差異會引起非共光路像差（NCPA）。由于波前檢測子系統無法檢測到成像子系統內的靜態像差，AO 系統在閉環校正過程中也無法測量和補償該像差。此外，共光路部分也存在靜態像差，該像差主要由可變形鏡的面型引起。上述靜態像差的存在使得AO 系統的成像質量顯著下降[13]，必須要在自適應光學系統閉環校正之前預先校正[14-15]。

2012 年，Ren 和Dong 等首次將隨機并行梯度下 降（Stochastic Parallel Gradient Descent,SPGD）算法應用到AO 系統靜態像差校正中，并提出一種基于焦面能量優化方法的靜態像差校正技術[16]。通過控制可變形鏡，改變其面型，將科學成像路徑的焦面能量集中到艾里斑內以獲得高SR。然而根據過去的經驗，焦面能量優化方法在系統初始像差較大的情況下容易陷入局部極值，難以獲得全局最優的校正結果。

接著，Ren 和Zhang 等提出一種基于瞳面的靜態像差校正方法[17]。該方法使用一個參考點光源經準直后產生的平面波作為參考波前，并使用夏克哈特曼波前傳感器（SH-WFS）記錄參考波前，之后通過迭代優化算法將參考波前復制到AO 系統。參考波前為整個校正提供了優化方向，因此該方法可以快速校正系統的靜態像差，并且容易獲得全局最優解。然而該方法在校正過程中需要使用一臺額外的波前傳感器和激光光源且實驗流程相對復雜。

基于上述問題，本文提出一種基于焦面復制方法的AO 系統靜態像差校正技術。該技術利用點光源產生的完美PSF 作為參考圖像，使用迭代優化算法直接將參考PSF 圖像復制到系統成像路徑來校正系統內的靜態像差。與瞳面校正方法復制波前相比，該方法直接復制系統焦面PSF 圖像，優化速度更快，而且更加容易獲得全局最優解。

2 校正原理

2.1 校正系統

圖1 為校正系統原理圖。激光器發出的光被透鏡L1 準直后，經過擺鏡（TTM）和可變形鏡（DM）反射，由分束鏡（BS）將光束分別投射到波前傳感器路徑和科學相機成像路徑中。波前傳感器路徑由透鏡L2、L3、微透鏡陣列MLA 和波前檢測相機構成；科學成像路徑的光束經過成像透鏡L4 后直接成像在科學成像相機上（位置1）。在靜態像差校正時，將科學相機移走，光經過透鏡L5 再次成像到靜態像差校正相機（位置2）。

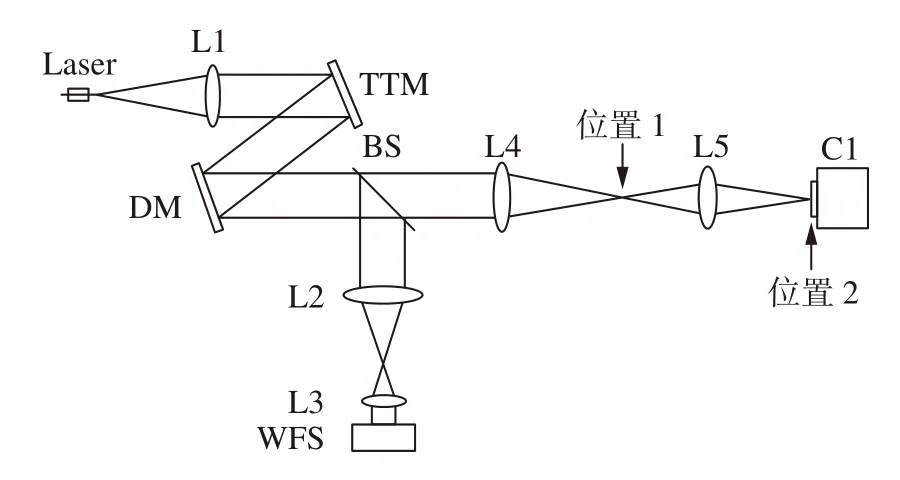
圖1 校正系統原理圖Fig.1 Block diagram of the correction system

實驗步驟如下：

（1）在成像透鏡L4 焦點位置上放置一個點光源作為參考光源，該光源經過透鏡L5 成像在靜態像差校正相機C1 上，該圖像將作為參考PSF（該過程只需要執行一次，后續可以直接調用該圖像）；

（2）移出參考光源，執行靜態像差校正。

校正完成后，將科學相機C1 重新安裝在位置1 即可開展科學觀測。

2.2 校正算法

本文采用隨機并行梯度下降算法校正AO 系統的靜態像差。SPGD[18-20]最早由Vorontsov 提出，并一直被用于自適應光學校正，它基于傳統的梯度下降算法的改進，通過對每個控制變量（DM 促動器電壓值）同時施加微小的隨機擾動量，隨后計算評價函數(Metric Function)的變化，并以此尋找梯度下降最快的方向進行下一次迭代，直到評價函數收斂于期望值。在每一次迭代優化過程中，施加的微小的隨機擾動量會重新生成，用以產生多種梯度方向，供算法評估，進而保證評價函數收斂。SPGD 算法中每次迭代的控制變量迭代公式：

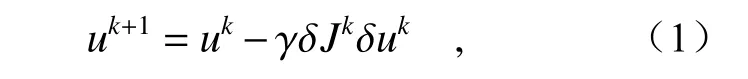
其中，k為迭代次數；DM 促動器的控制電壓可以表示為：u=u1,u2,···,un，n為優化變量的個數（DM 的促動器數量,本文實驗中為 97 個）；γ 為增益系數，當評價函數向極小值方向優化時，γ為正值，反之，γ 為負值；δu為施加的隨機擾動且服從伯努利分布；評價函數變化值為 δJ：

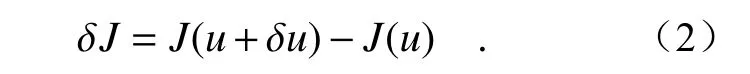
通常使用雙邊擾動以提高評價函數變化值的計算精度。

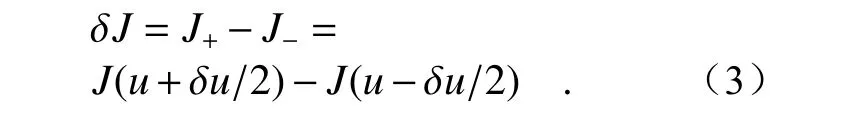
為了實現焦面PSF 圖像的復制，本文提出了一種專門用于優化焦面復制方法的系統評價函數。該評價函數用于將參考PSF 圖像復制到AO 系統焦面，進而實現系統內靜態像差的校正。假設PSF 圖像大小為m×n個像素，i(x,y)表示AO 系統焦面圖像每一點像素強度，imax，imin分別表示系統圖像上像素強的最大和最小值。iref(x,y)表示參考圖像每點像素值，irefmax，irefmin分別表示參考圖像上像素的最大和最小值。在使用公式(4)和(5)對圖像歸一化后，系統評價函數可以表示為，

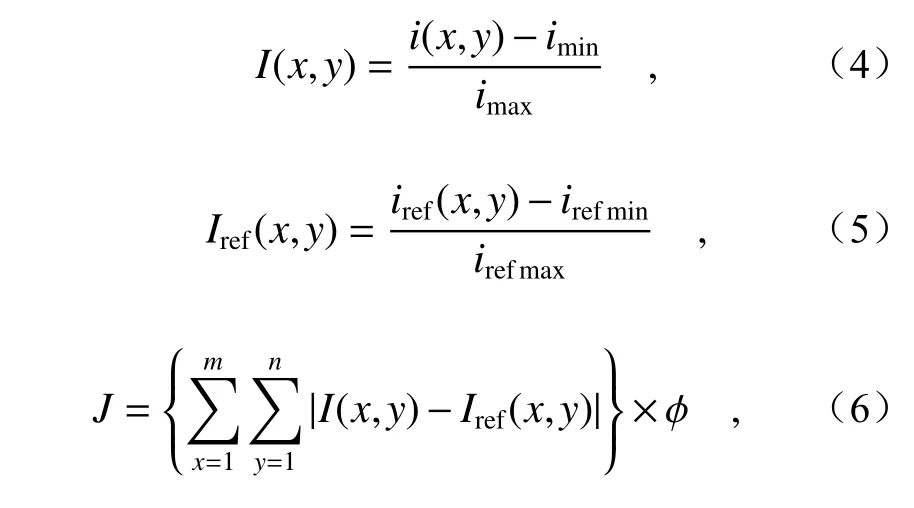
其中，?為影響系數，取值范圍為（0.000 1,1），用于保證評價函數的動態范圍和收斂。由公式（6）可知，理論上當評價函數的值為0 時，參考圖像被完全復制到AO 系統成像路徑。但實際校正過程中，由于相機噪聲和外部環境的影響，系統評價函數J無法被優化到0。通常情況下，當評價函數J收斂到0.45～0.55 內時，影響系數 ?的數量級為0.001～0.01，優化區域內歸一化后各像素點的差值|I(x,y)?Iref(x,y)|的平均值為0.007～0.015，反向歸一化后可得實際各個像素點的差值的平均值在500～1 000（imax=irefmax,imin=irefmin）。考慮到相機噪聲和外部環境的影響，此種差值情況下，兩張PSF 圖像此時可以視作基本一致。

此時波前檢測相機將記錄優化后的DM 電壓對應的波前，用于后續的AO 系統閉環校正。

3 實驗研究

實驗系統的光源采用波長為632.8 nm 的氦氖激光器。可變形鏡采用ALAPO 公司生產的97 單元連續鏡面的可變形鏡（DM），促動器排列11×11。圖2（a）為拍攝的系統初始焦面PSF 圖像，從圖中可知系統焦面存在較大初始靜態像差。圖2（b）為校正后的焦面PSF 圖像，從圖中可以看出，校正后系統內的靜態像差被有效校正，校正后的系統焦面PSF 圖像和參考PSF 圖像基本相同。圖2（c）為拍攝的參考PSF 圖像（參考PSF 提前拍攝并保存，校正過程只需要讀取圖像即可）。按照遠場定義公式計算并使用參考圖像作為標準圖像。在使用焦面復制技術校正后，SR 從初始的0.312 提升到0.995。

圖2 焦面PSF 圖像。（a）初始圖像；（b）校正后圖像；（c）參考圖像Fig.2 The focal-plane PSF image.(a) Initial image;(b) corrected image;(c) reference image

圖3 為評價函數曲線，在校正約15 000 步后，系統評價函數從初始的2.1 下降到0.49，繼續優化評價函數不會再下降。實驗結果表明基于焦面復制方法的SPGD 校正技術能有效校正AO 系統的靜態像差。

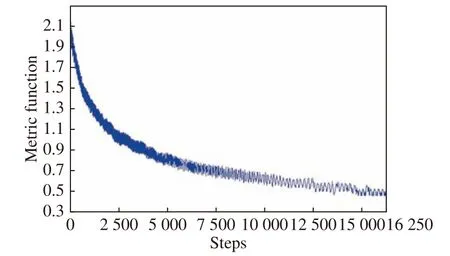
圖3 評價函數曲線Fig.3 Metric function curve

為了進一步定量分析校正效果，本實驗使用Thorlabs 公司生產的WFS-150-5C 波前傳感器，分別測量了校正前后的RMS。測試結果表明在校正后AO 系統的RMS 波前誤差從初始的110 nm下降到7 nm。表1 為校正前后各項Zernike 多項式系數（使用Zernike 多項式前15 項進行波前重構，其中不包括平移、X軸傾斜、Y軸傾斜和離焦）。從表1 可知，校正后，Zernike 多項式各項系數明顯減小，這也證明了本文校正技術可以有效校正AO 系統成像路徑的靜態像差。圖4（彩圖見期刊電子版）為校正后的AO 系統的波面。

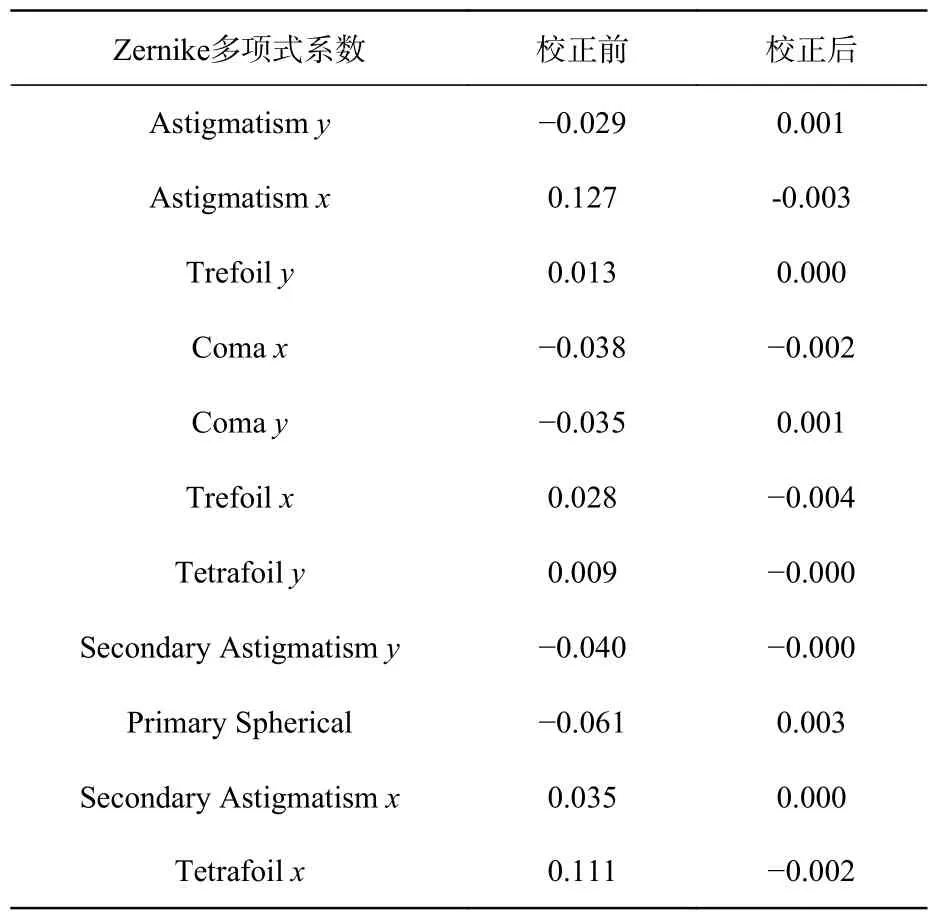
表1 校正前后系統各項Zernike 系數Tab.1 Zernike coefficients of the system before and after correction

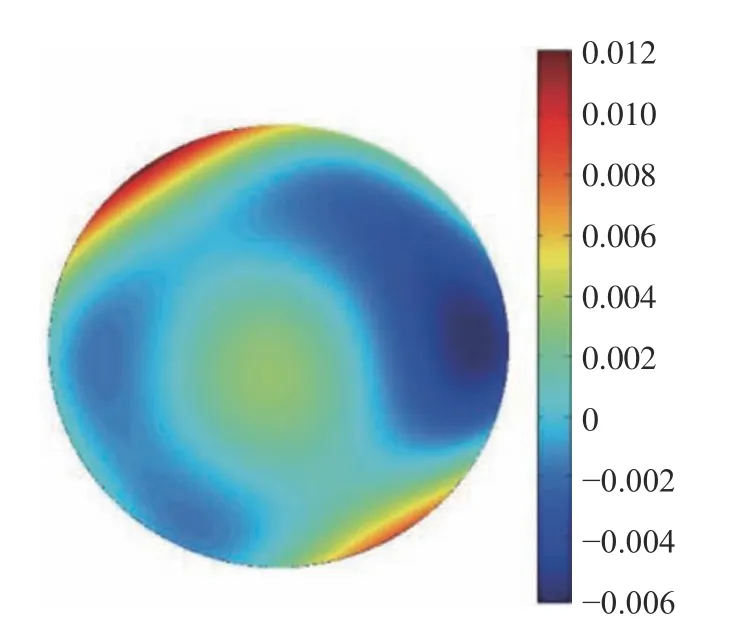
圖4 校正后波前圖Fig.4 The corrected wavefront map

4 對比實驗與分析

為了說明本文提出的焦面復制技術優于先前提出的焦面能量優化方法和瞳面校正法。本節將在相同的實驗環境下分別比較3 種方法的校正效果。圖5（彩圖見期刊電子版）為使用焦面能量優化方法校正后的焦面PSF 圖像和波前圖。在初始靜態像差較大的情況下，采用焦面能量優化方法校正后的，SR 從初始的0.312 提高到0.739。RMS 從初始的110 nm 下降到55 nm。整個校正過程需要迭代約70 000 步。圖6 為瞳面方法校正后PSF 圖像和波前圖，使用瞳面方法校正后的SR 提高到0.988，波前RMS 下降到11 nm，整個校正過程需要迭代約40 000 步。表2 為3 種方法校正后各項Zernike 多項式系數對比。

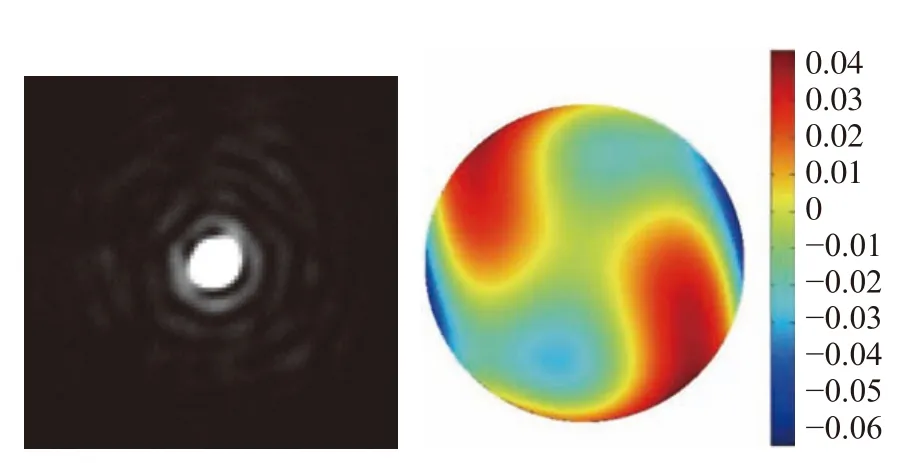
圖5 焦面能量優化方法校正后焦面PSF 圖像和波前圖Fig.5 PSF corrected by the focal plane energy optimization method and the corresponding corrected wavefront map

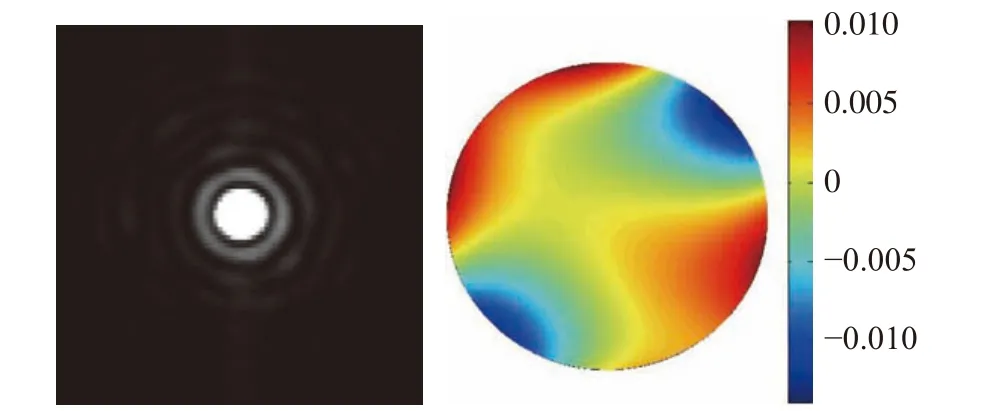
圖6 瞳面方法校正后PSF 圖像和波前圖Fig.6 PSF corrected by the pupil plane approach and the corresponding corrected wavefront map

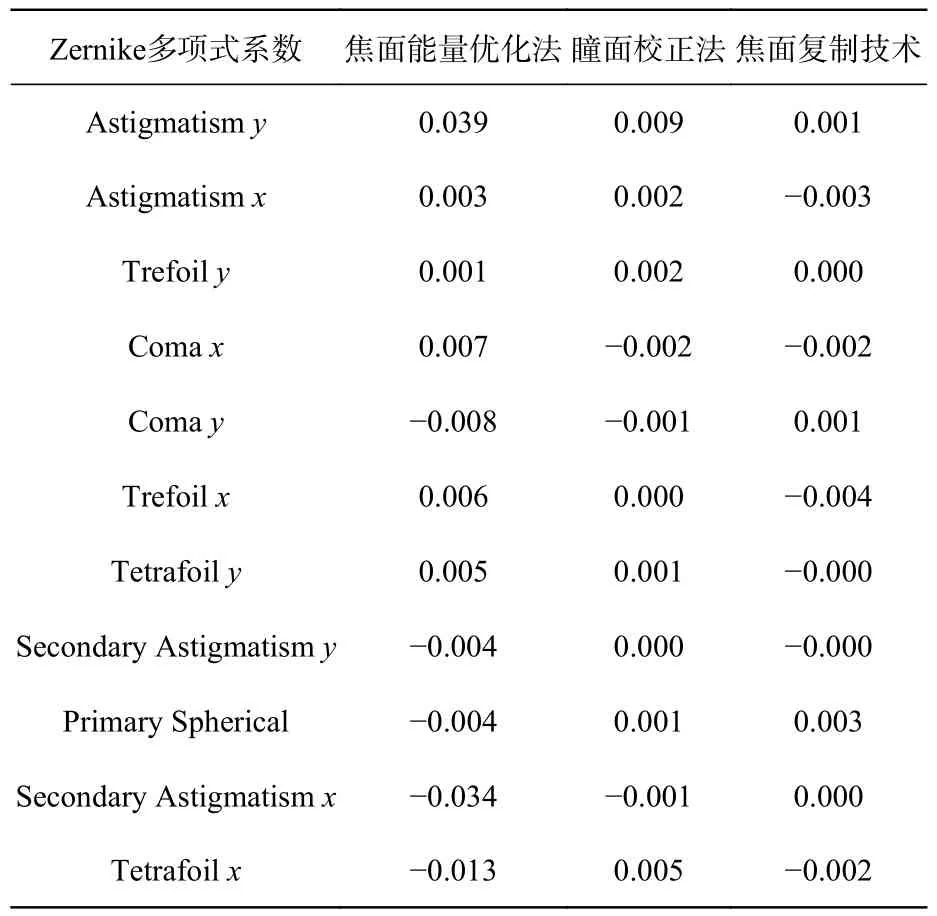
表2 3 種方法校正后Zernike 系數Tab.2 Zernike coefficients corrected by 3 kinds of methods

從校正結果（SR）可以看出，本文提出的焦面復制技術與焦面能量優化方法相比，SR 提高了34.6%。而與瞳面校正法校正結果幾乎相同。從校正時間上來分析，本文提出的焦面復制技術比瞳面校正法快了2.67 倍。此外本文提出的焦面復制技術只需要在AO 系統后額外增加一塊透鏡就可以實現靜態像差的校正，易于實現且不會在AO 系統中引入額外的像差。

5 結論

本文提出了一種基于焦面復制的AO 系統靜態像差校正技術。采用參考光源產生的高質量PSF 圖像作為參考圖像，通過迭代優化算法控制可變形鏡將參考PSF 圖像復制到AO 系統成像路徑。實驗結果表明校正后AO 系統的SR 從初始的0.312 提升到0.995。本文還分別在相同的實驗條件下，對3 種方法進行比較。測試結果表明：本文提出的基于焦面復制的靜態像差校正技術在獲得相同校正結果的情況下，校正速度明顯優于其他方法，而且該技術器件簡單易于實現。該校正結果不僅遠遠滿足傳統的自適應光學系統對成像質量的需求，還滿足ExAO 系統對像質的需求。但是本文方法如應用于配備幾百甚至上千單元可變形鏡的自適應光學系統，校正速度會有所下降。下一步準備在本文研究成果基礎上，提升校正速度，并應用于項目組研制的系外行星高對比度成像星冕儀系統中。