從數系擴充認知指數函數的概念

孫德榮 高全祖 劉 雪

（1.昌吉學院數學與數據科學學院 新疆 昌吉 831100；2.昌吉州第一中學 新疆 昌吉 831100）

函數是大學數學專業數學分析課程的研究對象，基本初等函數冪函數、指數函數、對數函數又是中學數學教學的一個重要內容，指數函數作為高中生學習函數的開始，對后續函數的學習起著基礎性的作用，它是將冪指數從整數范圍擴充到實數范圍之后，建立的第一個重要的基本初等函數。我國現行的中學數學教材一般是從數系的擴張出發來構建數學運算的，學生對指數函數的認知也是從正整數集到實數集內的冪指數運算開始的。數學師范生在完成數學學科專業課學習之后，已經具備了足夠的學科知識，可以從數系擴張的角度來重新認識與完善指數函數的相關知識體系，以提高自身的專業與學科核心素養，更好的指導中學數學教學。［1］

1 有理數域內冪指數運算的建立與完善

對指數函數的認識關鍵在于對冪指數概念的構建與運算性質的理解，隨著學生對自然數、整數、有理數、實數和復數等相關數系知識的逐步認識，在不同的學習階段對冪指數的概念與性質也逐步得到完善，最后形成了較為完整的指數函數概念。

這里全體非負整數的集合稱自然數集，用字母“N”來表示，包含正整數和零；N+表示正整數集；Z表示整數集；Q表示有理數集；R表示實數集；C表示復數集。

1.1 整數集內冪指數概念的建立

中學數學教材［2］由幾何意義出發，從一個數的平方、立方，引導學生認識了一個數的n次方的整數冪的概念與性質。即

一個數a與它自身的乘積叫做這個數的平方（或二次方），記作a×a=a2，例如，在幾何中，邊長為a的正方形的面積為S=a×a=a2。

三個相同的數a的乘積叫做這個數的立方（或三次方），記作a×a×a=a3，例如，在幾何中，棱長為a的立方體的體積為V=a×a×a=a3。

n個相同的數a的乘積叫做a的n次方，記作a×a×…×a=an。an也稱為a的n次冪，其中a叫做底數，n叫做冪指數，這里n∈N+。

利用冪的概念以及乘法與除法的意義，容易推導出正整數指數冪的運算法則：

法則1：am·an=am+n(m,n∈N+)；法則2：法則3：(am)n=amn；

法則4：(a·b)n=an·bn；法則5：a0=1(a≠ 0)。

在整數范圍內，初中生學習乘法的意義之后，又有了相應的負整數冪和零指數冪的規定，冪的運算性質的邏輯推理也就完善了。中學數學教材通過以上方式給學生建立了整數冪的嚴密邏輯體系。

1.2 冪指數運算在有理數域內延拓

現行人教版普通高中課程標準實驗教科書［3］在引入了根式運算之后，就將冪指數概念擴展到了有理數域范圍內。

首先教材［4］給出根式的意義：一般地，如果xn=a，那么x叫做a的n次方根，其中n＞1，并且n∈N+。當n是奇數時，正數的n次方根是一個正數，負數的n次方根是一個負數，表示為。當n是偶數時，xn=a是一個正數，正數a的n次方根有兩個，這兩個數互為相反數，表示為。其中，式子叫做根式，n叫做根指數，a叫做被開方數。

其次教材［5］從幾個特殊的實例出發，如：探究歸納分數指數冪的運算規律，給出如下定義：

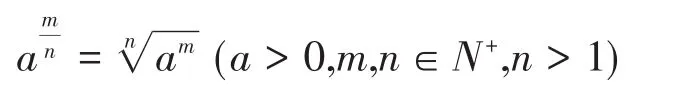
另外，1）對負分數指數冪給出了與負整數指數冪相仿意義的規定：

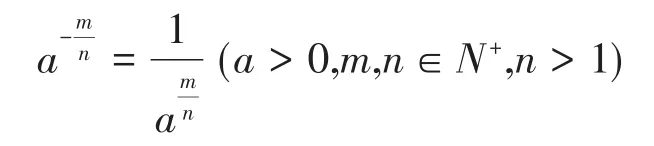
2）規定0的正分數指數冪為0，0的負分數指數冪沒有意義。

以上規定將整數指數冪的概念推廣到了有理數域。

最后教材［6］給出結論：整數指數冪的運算性質對于有理數指數冪也同樣適用，即

（1）aras=ar+s(a＞ 0,r,s∈Q);

（2）(ar)s=ars(a＞ 0,r,s∈Q);

（3）(ab)r=arbr(a＞0,b＞0,r∈Q).

存在的問題是教材并未對定義的合理性（當m不能被n整除時）與運算性質的正確性給予說明或證明（教材的編寫缺乏邏輯嚴密），如果教師在教學中也如同教材一樣一帶而過，那就會造成學生認知結構上的邏輯缺失。按照高中生現有的認知水平，運算性質（1）—（3）是可以證明的。事實上，對運算性質的證明，也就是對定義合理性的有力佐證。

為了證明有理數指數冪的運算性質，要補充證明以下三個性質：

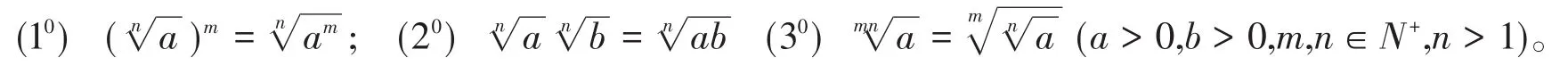
性質（10）—（30）也并不是顯然的，證明如下：

證明 設a＞0,b＞0,?m,n∈N+,n＞1.

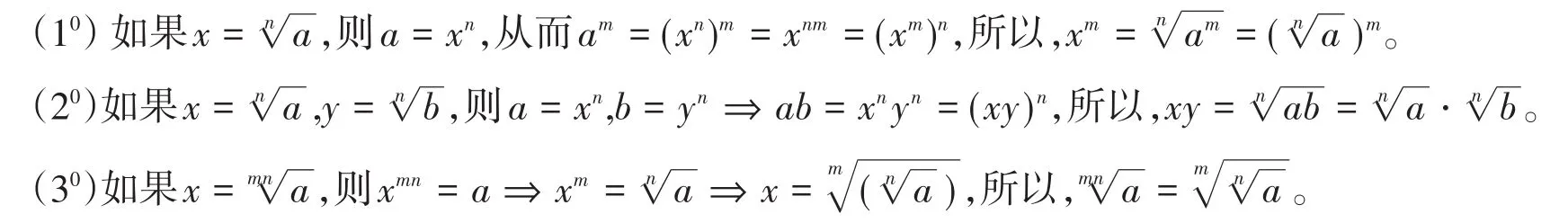
根據分數指數冪的定義以及性質（10）—（30），對性質（1）—（3）的證明如下：

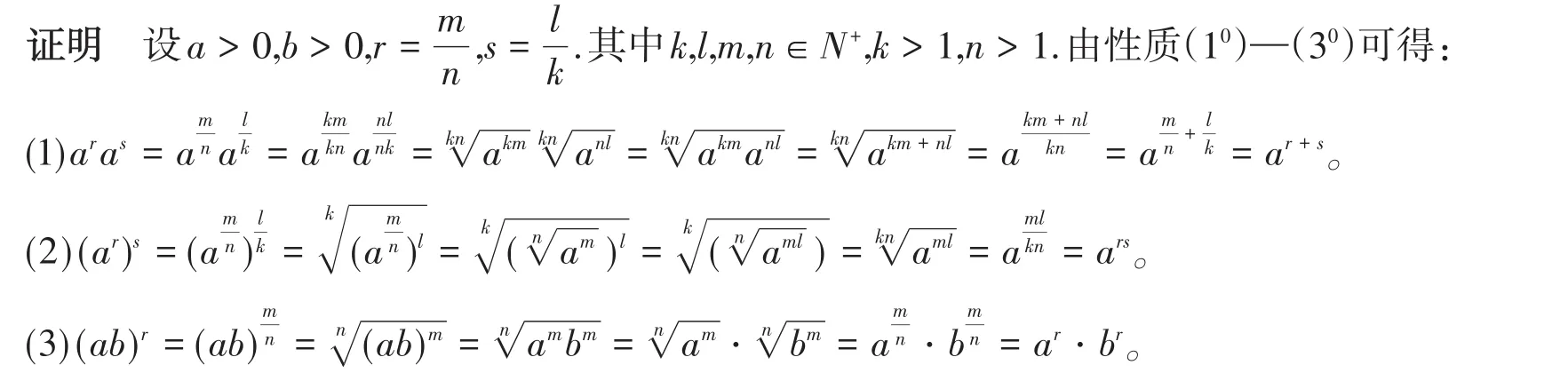
從以上推理可以看到，有理數指數冪的性質并不是顯然的。在學生已有的認知水平上，通過推理證明自然得到分數指數冪的性質，既說明了定義的合理性又完善了知識結構的邏輯嚴密性。這樣，冪指數運算在有理數域內的延拓就沒有什么遺憾了。

2 實數域內指數函數概念的建立與完善

對于a＞0(a∈R)來說，任意一個有理數x都滿足一個與它對應的有理指數冪ax＞0，這樣就能夠把整數指數運算擴展到有理指數冪的運算。我國現行的高中數學教材中［7］直接給出了實數域內指數函數的概念：一般如y=ax（a＞0，且a≠1）的函數叫做指數函數，函數的定義域是R。這里如果x為有理數，那么學生根據有理數冪指數的運算知道函數值ax的意義，但是當x為無理數時，ax的意義為何？之前學生并沒有認識，高中教材采取了以一個特例的實驗觀察法告訴學生，對任意一個無理數x，ax都唯一對應一個實數，這是高中數學在實數域內介紹指數函數的邏輯不嚴密所在。

大學數學在建立了實數極限理論的相關知識和概念之后，就可以完善指數函數在實數范圍內的定義。首先大學數學專業的數學分析課程中，通過級數理論可以建立有理數與無理數之間的運算。

由上述命題可知，如果a0.a1a2…an…是一個無理數（無限不循環小數），并且Sn=a0.a1a2…an，那么，即：任意無理數都是一個有理數列的極限。

大學數學分析教材，在介紹了實數理論的相關理論之后，給出了確界的概念與確界存在唯一性定理。

定義1［8］（上確界） 設S是R中的一個數集，η是一個實數，若滿足

①對任意x∈S，有x≤η，即η是S的上界；

②對任意a＜η，存在x0∈S，使得x0＞a，則稱數η是數集S的上確界，記為η=supS。

定義2［9］（下確界） 設S是R中的一個數集，若ξ是一個實數，滿足

①對任意x∈S，有x≥ξ，即ξ是S的下界；

②對任意β＞ξ，存在x0∈S，使得x0＜β，則稱數ξ是數集S的下確界，記為ξ=infS。

從定義1與定義2可知，S上確界η=supS是S的最小上界，S下確界ξ=infS是S的最大下界。

定理［10］（確界唯一性） 設S?R是非空數集.若S有上界，則S必有上確界；若S有下界，則S必有下確界。

有了以上實數的極限理論基礎，就可以建立以下實數域內指數函數的精確定義：

定義3［11］給定實數a＞0，a≠1設x為無理數，我們規定

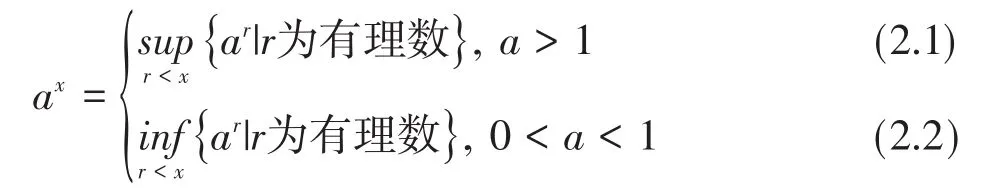
對任一無理數x，必有有理數r0，使x＜r0，則當有理數r＜x時，有r＜r0。由有理數乘冪的性質知：當a＞1時，有ar＜ar0。這表明非空數集{ar|r＜x,r為有理數} 有一個上界ar0。根據確界原理，該數集有上確界，所以(2.1)式右邊是一個確定的定數。同理，當0＜a＜1時，(2.2)式右邊也是一個定數。

如果把(2.1)、(2.2)兩式中的“r＜x”改為“r≤x”，那么，無論r是無理數或是有理數，ax都可以用上述確界形式來統一表示。

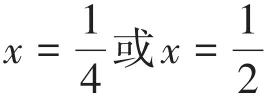
綜上所述，規定：當a＞0且a≠1時，指數函數y=ax定義域為R。這樣，指數函數的概念在實數范圍內才得以完善。實數域內指數函數的性質也可以由極限運算法則得到，這里不再贅述。

3 指數函數在復數域內的延拓

現行的人教版高中數學教材［13］給出了復數概念與幾何意義，并初步討論了復數代數形式的四則運算，首先利用直角坐標與極坐標的關系，將非零復數z=x+iy表示為三角形式：

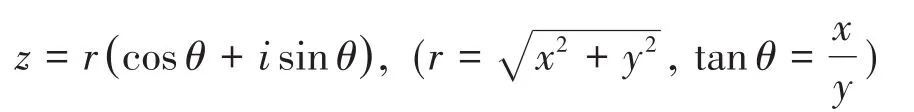
這里當r=1時，z=cosθ+isinθ，按照教材的闡述，如果利用歐拉公式

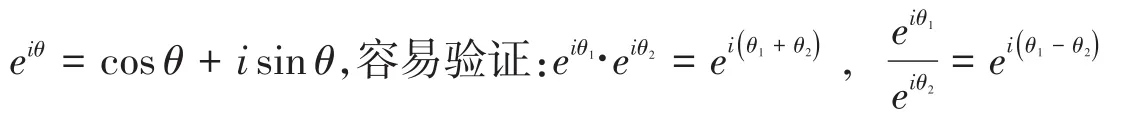
這樣就得到了復數的指數形式：z=reiθ。教材存在的邏輯問題是：歐拉公式從何而來？

大學數學專業的課程體系中，通過數學分析與復變函數課程所建立的級數理論，為在復數域內推廣指數函數奠定了基礎。1715年英格蘭數學家B.Taylor（1685-1731）提出了函數的冪級數表示公式［14］，其中指數函數ex(x∈R)的函數值可以由下面的冪級數得到，即：

由（3.1）來定義

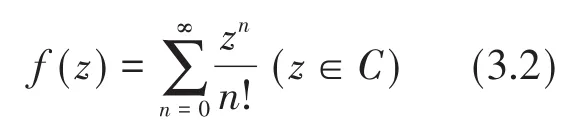
顯然f(1)=e，由冪級數的性質和運算法則可以證明f(z)是連續的，并且f(z1+z2)=f(z1)f(z2)，當z=x∈R時，f(z)=ex，所以記f(z)=ez，因此，指數函數就在復數域內得到了推廣，即

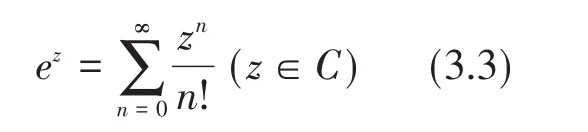
利用（3.3）可以證明著名的歐拉公式：eiθ=cosθ+isinθ。這樣，中學教材中的復數指數表示才得以邏輯完整。

對于復指數函數ez，具有如下的性質：

（1）對于實數z=x（y=0）來說，定義與實指數函數的定義是一致的。

（2）ez|=ez＞0，argee=y；在z平面上ez≠0。

（4）對任意整數k，有ez·e2kπi=ez，因f(z+2kπi)=f(z)，所以ez是以2πi為基本周期的周期函數。

以上只是給出了復數域內一個常用的指數函數ez的定義，大學復變函數［15］給出了一般指數函數定義ω=az=ezlna(a≠0,∞,a∈C)。它是無窮多個獨立的單值解析函數，詳情這里不再贅述。

4 結論

深入分析中學數學教材的知識體系，對教材邏輯缺失部分進行補充與完善，為師范生構建一個較為嚴密的數學認知邏輯結構，對提高中學數學教師專業素養，培養合格的中學數學教師具有深遠意義。數學師范生正處在數學知識體系構建與完善過程中，在數學學科相關課程學習完成后，有必要對初等數學知識進行再建與重構，這對指導中學數學教學有深遠意義。