真實人體呼吸道湍流仿真方法分析
崔 巖, 王玉龍, 董榕波, 李 蕾, 李 海, 馬松云, 劉銀水
(1.華中科技大學 機械科學與工程學院, 湖北 武漢 430074;2.中國人民解放軍95829醫院, 湖北 武漢 430022;3.華中科技大學 同濟醫學院附屬協和醫院兒科, 湖北 武漢 430030;4.亞琛工業大學 機械工程學院通用力學研究所, 德國 亞琛 52062)
引言
吸入給藥是利用肺泡具有較大表面積、毛細血管豐富、物質交換短和藥物吸收快等優點,將藥物粉末/液滴分散,經由口腔進入呼吸道,最終進入血液循環以達到預防和治療呼吸系統疾病的一種高效治療手段[1]。目前吸入給藥存在藥物輸送效率較低的突出問題,會急劇增加患者的醫療成本,若過量用藥則會損害患者的身體健康。藥物顆粒在呼吸道內的沉積主要受慣性沉積、湍流擴散沉積以及顆粒布朗運動的影響[2],其中湍流擴散沉積起主導作用。因此,精準的求解人體呼吸道的湍動能場,是研究提升吸入給藥效率的根本前提。
人體支氣管樹結構復雜,呼吸道截面變化巨大,其流動雷諾數存在較大的變化范圍(Re=500~8000)[3]。因此,需借助可靠的湍流模型預測包含層流到湍流過渡轉變、剪切流和回旋流等復雜流態。目前,何種湍流模型能夠高效精準求解呼吸道流場依舊是一個開放性問題[4]。使用直接數值模擬(Direct Numerical Simulation, DNS)的方法求解瞬時Navier-Stokes(N-S)方程,以此對湍流進行完全解析是最為精確的。但其存在仿真耗時長,所需計算資源龐大等問題,難以高效的求解呼吸道流場[5]。若僅考慮對湍動能場起主導作用的大尺度的渦,而對小尺度的渦采用數學模型加以刻畫,即大渦模擬仿真(Large Eddy Simulation, LES),則可有效降低DNS仿真中的網格數量。JAYARAJU等人[6]和LAMBERT等人[7]通過使用LES模型對簡化的上呼吸道模型仿真后發現,LES所計算的速度和湍動能場與實驗數據保持較高的一致性。LIN等人[8]分別使用DNS和LES模擬分析了同一呼吸道模型的內部流場特性,結果表明LES能夠較好的模擬流場中的回旋流,且與DNS得到的仿真結果高度吻合。但是,LES本質上還是一種DNS方法,其流場仍需大量網格來表征[9],計算耗時較長。然而,從臨床角度出發,醫生希望能在短時間內得到呼吸道流場的仿真模擬結果,以此對呼吸系統疾病做出精準的診斷。
雷諾平均N-S方程(Reynolds-averaged Navier-Stokes, RANS)則不求解瞬時的N-S方程,轉而計算時間平均湍流場。如此,流場表征所需的網格數量可顯著降低,進而有效提升了流場的計算效率[10]。常用的RANS模型包括渦黏模型(兩方程的k-ε模型和k-ωSST模型,以及四方程的Transition SST模型等)和雷諾應力模型(七方程的RSM-SSG模型)。ISLAM等[11]采用不同渦粘模型模擬呼吸道內部流場后發現,k-ωSST模型計算上呼吸道內的湍流時要優于標準的k-ε模型。XU等[12]分別考慮了吸氣和呼氣兩個過程,采用不同的RANS模型得到的結果與PIV實驗結果進行比較后發現Transition SST模型更適用于吸入過程的湍流場仿真,而k-ωSST模型則更適用于呼出過程的仿真。ELCNER[13]通過對簡化的呼吸道模型進行仿真模擬,分析比較了k-ε、k-ω和LES三種湍流模型。結果表明LES的結果與實驗結果的吻合度最高,其余湍流模型計算得到的喉部下游流動區域的流場與實驗結果存在較大區別。雖然k-ε和k-ω湍流模型均能得到流場的全局特征,但難以較好的求解流速較低時的低雷諾數區域和過渡流區域。
結合Spezial-Sarka-Catski(SSG)模型[14]的雷諾應力模型(RSM)摒棄了各項同性渦粘假設,通過求解雷諾應力傳輸方程和耗散率方程,以封閉雷諾平均N-S方程。RSM模型比兩方程模型更嚴格地計算了流線曲率、渦流、回旋流的變化對流場的影響,因此它在計算復雜湍流流動時具有更高優勢。SOMMERFELD等人[15]通過分析對比RSM模型和RANS模型后發現,使用k-ε模型計算得到的呼吸道流場難以精準的表征湍流邊界層,使用k-ωSST計算的流場能夠很好的捕捉到粘性底層與湍流層之間的混合流動區域的細節,各向異性的雷諾應力(RSM-SSG)湍流模型則能更好的計算近壁面的湍流場。
此外,由于真實人體支氣管樹結構復雜,過往相關研究均采用混合網格的方法劃分呼吸道內部流場,需要消耗巨大的計算時間和資源。然而,從臨床角度出發,醫生希望在48 h內給出基于CFD仿真的吸入給藥效率分析結果,先前的研究并不能滿足臨床需求。鑒于上述矛盾,若能采用全結構化網格劃分其流場,則能極大的降低網格的數量(相同尺寸的結構化網格數量僅為非結構化網格數量的1/3),并結合更適合真實人體呼吸道內湍流仿真模型,進而可高效的提升仿真模擬計算的精度和速度。
綜上所述,本研究提出使用全結構化網格劃分真實人體支氣管樹模型,并分別采用k-ωSST模型、Transition SST模型、雷諾應力模型(RSM-SSG)和大渦模擬(LES)計算呼吸道內部流場,并與實驗測量結果相對比,在確保可靠計算精度的前提下,探尋最適用于真實人體呼吸道流場的快速且精確的計算方法,為呼吸道計算流體力學仿真模擬的臨床應用提供參考和依據。
1 湍流模型
1.1 Shear-Stress Transport (SST) k-ω模型
SST模型是The Baseline (BSL)k-ω模型的改進,并在湍流黏度的定義中考慮了湍流剪切應力。這使得該算法在近壁區繞流和旋流方面比標準k-ω和BSLk-ω模型更精確。其湍動能k及耗散率ω的方程如下[16]:
(1)
(2)
式中,ui——i方向的平均速度
uj——j方向的平均速度
Γk——k的有效擴散系數
Γω——ω的有效擴散系數
Yk——k因湍流引起的耗散
Yω——ω因湍流引起的耗散
Gk——k引起的湍動能
Gω——ω引起的湍動能
Dω—— 交叉擴散率
有效擴散系數公式為:
(3)
(4)
式中,σk和σω——k和ω的紊流普朗特數
μt—— 修正后的黏度系數
(5)
式中,α*—— 抑制湍流黏度的低雷諾修正系數
S—— 剪切力張量的常數項
F2—— 湍流普朗特數的融合項
α1—— 常數
1.2 Transition SST模型
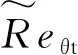
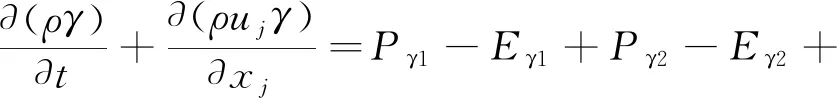
(6)
轉捩源項定義如下:
Pγ1=Flengthca1ρS[γFonset]cγ3
(7)
Eγ1=ce1Pγ1γ
(8)
Pγ2=ca2ρΩγFturb
(9)
Eγ2=ce2Pγ2γ
(10)
式中,S—— 應變率張量的模
Flength—— 轉捩區長度
Ω —— 漩渦強度
Fonset—— 渦量雷諾數ReV的函數
Fturb—— 黏性系數系數比的函數
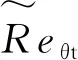
(11)
(12)

T —— 時間尺度
Fθt—— 由源項控制參數的混合參數
1.3 RSM模型
本研究采用的RSM模型為Spezial-Sarka-Catski的SSG模型,該模型已被證明在平面應變、旋轉平面剪切和軸對稱膨脹/收縮等一系列基本剪切流中具有優越的性能。典型的線性雷諾應力模型如下[20]:
(13)


Dij—— 擴散項
Pij—— 剪切應力產生項
Φij—— 壓力應變項
εij—— 和黏性耗散項
1.4 LES模型
對于LES模型,針對不可壓縮流動,經過濾波函數處理后的N-S方程和連續方程為[21]:
(14)
(15)
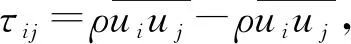

表1 四種湍流模型的優劣
2 仿真及實驗設置
2.1 真實人體支氣管樹模型
本研究所研究的呼吸道模型是根據一名成年男子的高分辨率計算機斷層掃描(CT圖片)獲得的呼吸道醫學影像,通過醫學影像三維重構軟件,生成的立體光刻(STL)三維幾何模型[26],如圖1a所示。三維重構后的支氣管模型包括進氣管、口腔、氣管和支氣管(7級)。氣管處的水力直徑約16~18 mm,第七級支氣管處的水力直徑約為2~3 mm,氣管橫截面面積變化之大和支氣管樹結構之復雜是呼吸道內部產生不同流動狀態的根本原因。由于實驗的需要,根據人體肺部五葉十八段的生理結構,末端支氣管被劃分為10個區域并與相應的出口連接。

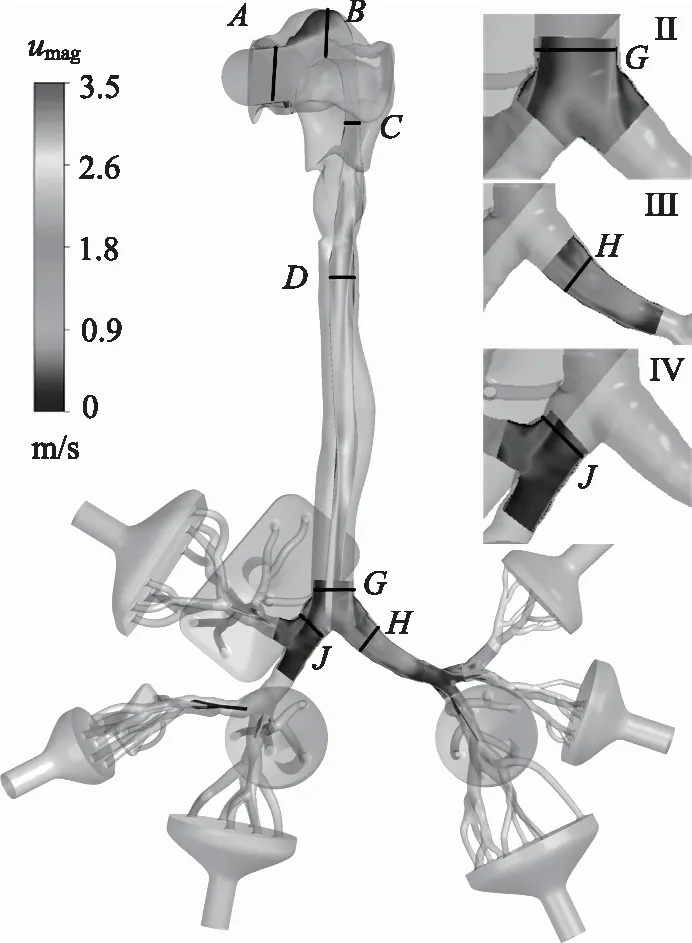
圖1 采用的真實人體呼吸道模型[26]
2.2 網格劃分
網格劃分是呼吸道仿真的重要環節之一,若網格計算單元質量低(網格非正交性和歪斜度偏高), 則會引發數值計算發散,進而影響流場的求解精度[27]。由于口腔的模型較為復雜,此處采用非結構化網格劃分。其余部位則充分利用ICEM CFD在結構化網格劃分方面的優勢,將支氣管樹及10個收集器全部采用結構化網格劃分。KOULLAPIS等[9]通過對比不同網格數量(700萬~5000萬)對結果的影響,發現在保持較好精度的條件下,采用700萬非結構化網格就能夠較好的解析呼吸道內的流動。對于同一個模型,相比于非結構化網格,使用結構化網格能夠大幅降低網格數量,且能更好的控制網格生成質量,使計算結果更易收斂。近壁面流動是影響顆粒沉積的主要原因[28]。為避免近壁面邊界層網格厚度過低從而影響壁面壓力梯度的求解精度,在網格劃分時近壁面貼合的網格層數保持在15層以上(如圖2所示)。該支氣管樹的網格總數約為1200萬。
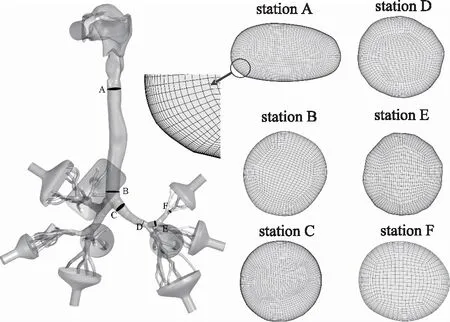
圖2 采用結構化網格劃分支氣管樹模型:結構化網格總數為900萬,呼吸道壁面邊界層網格層數大于15層
2.3 實驗設置與邊界條件
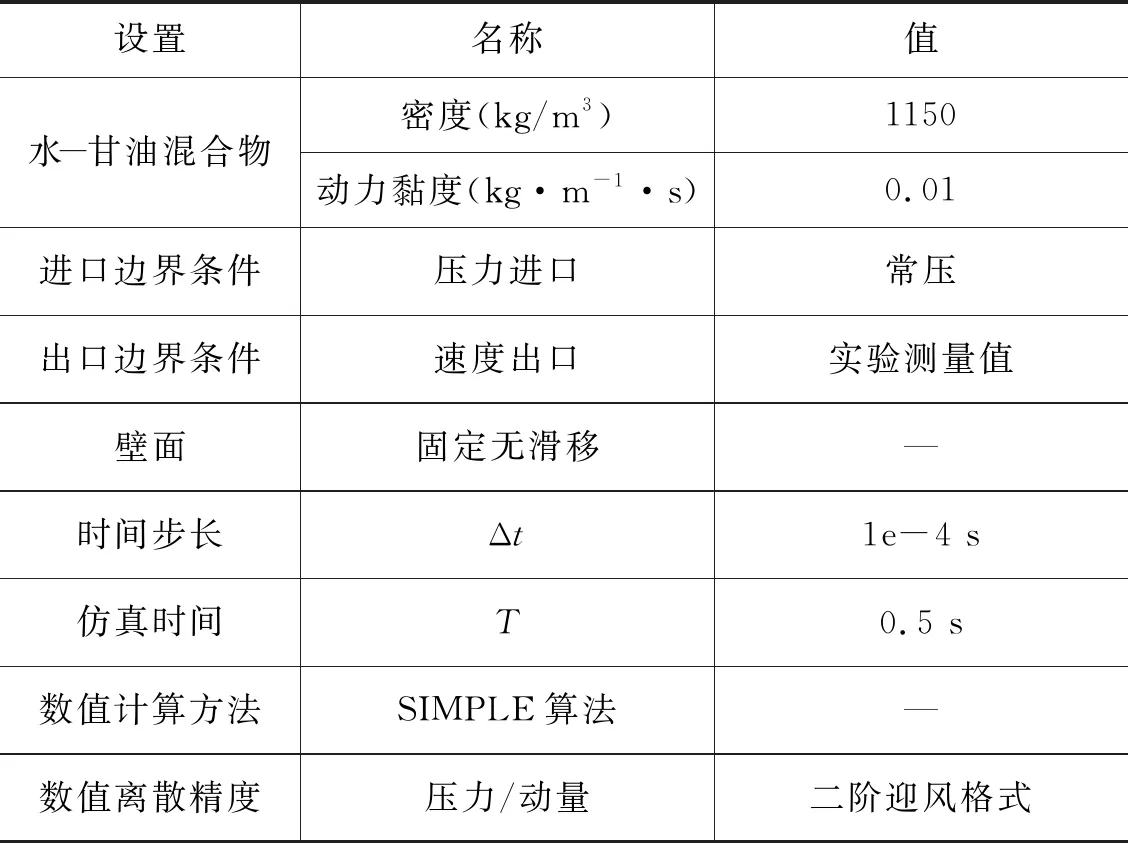
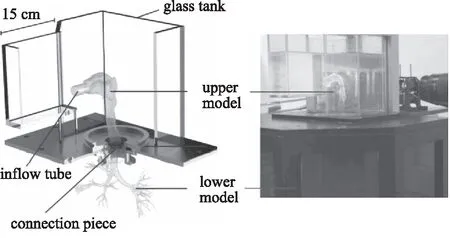
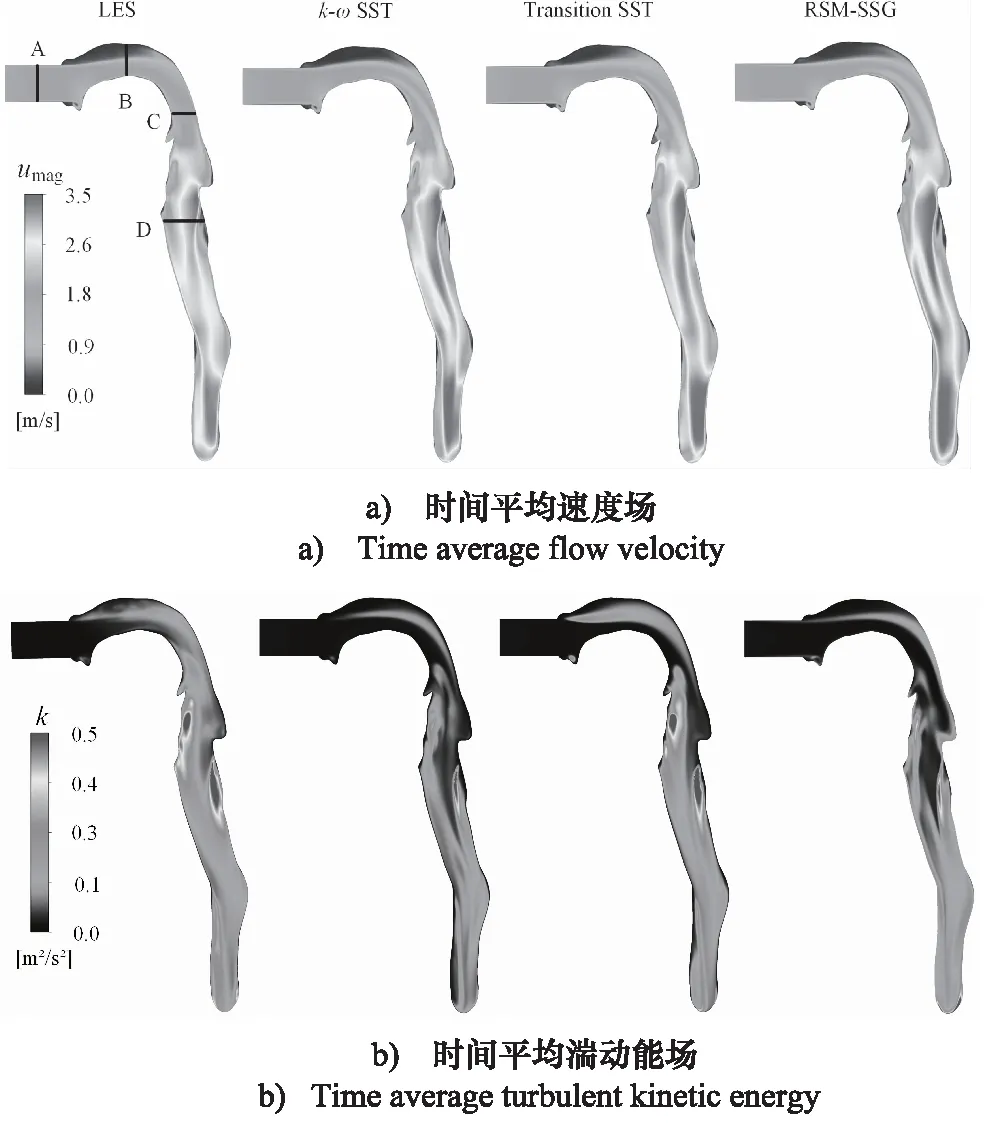
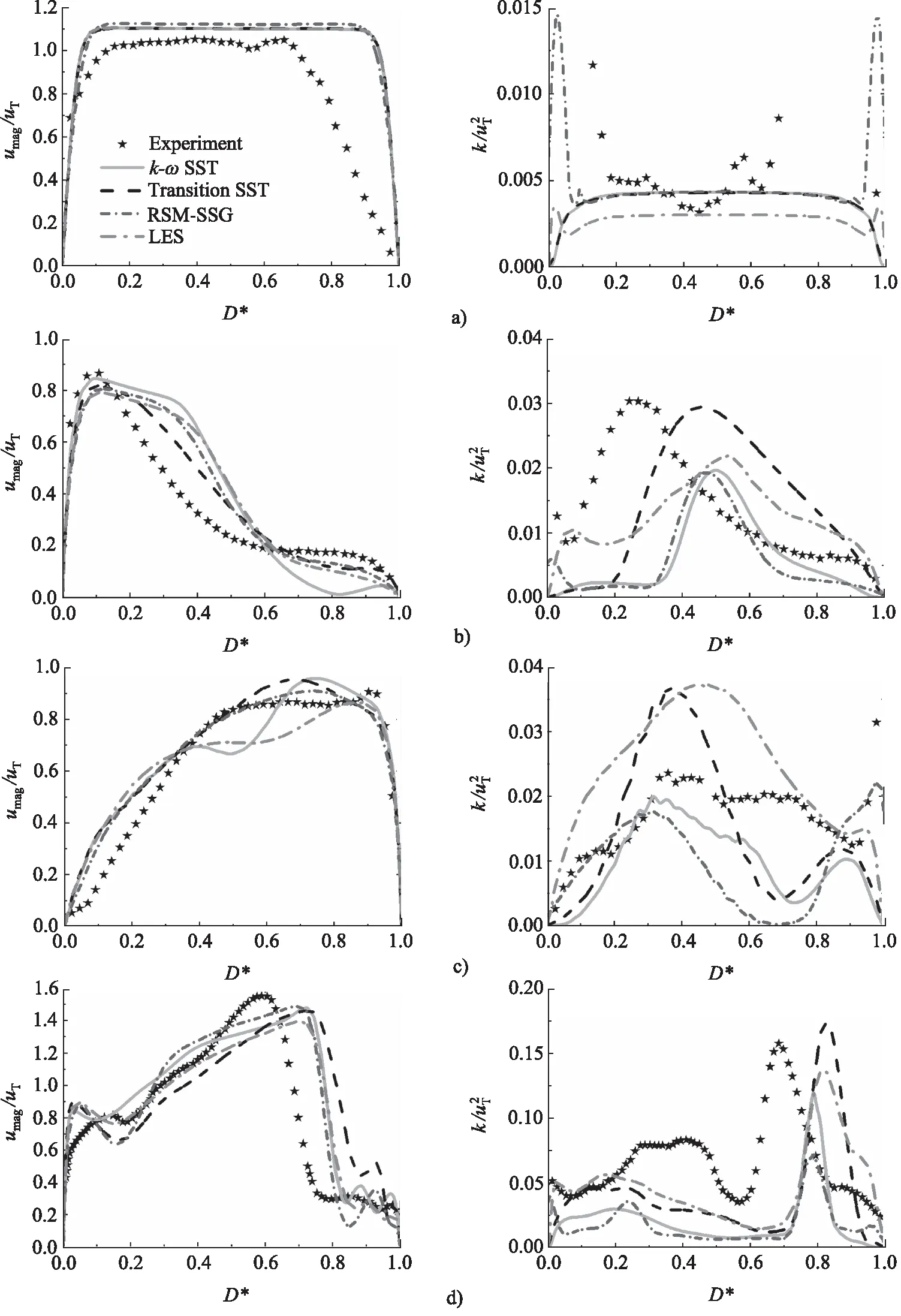
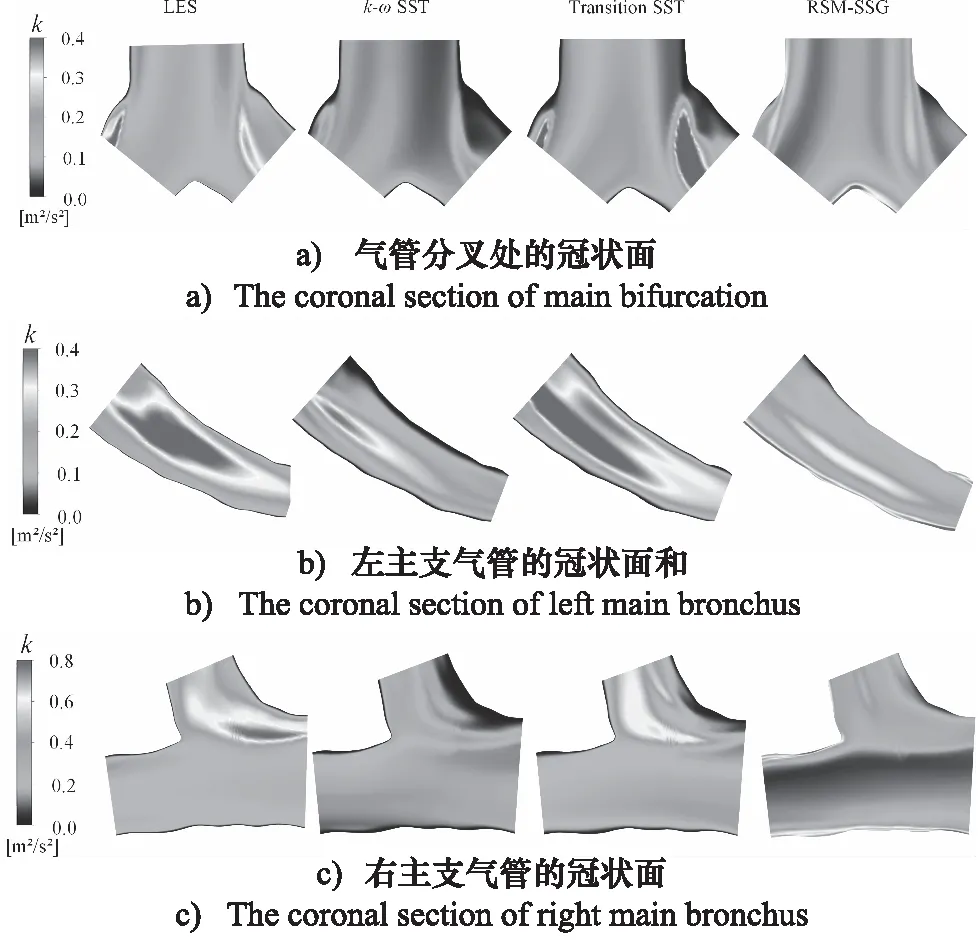
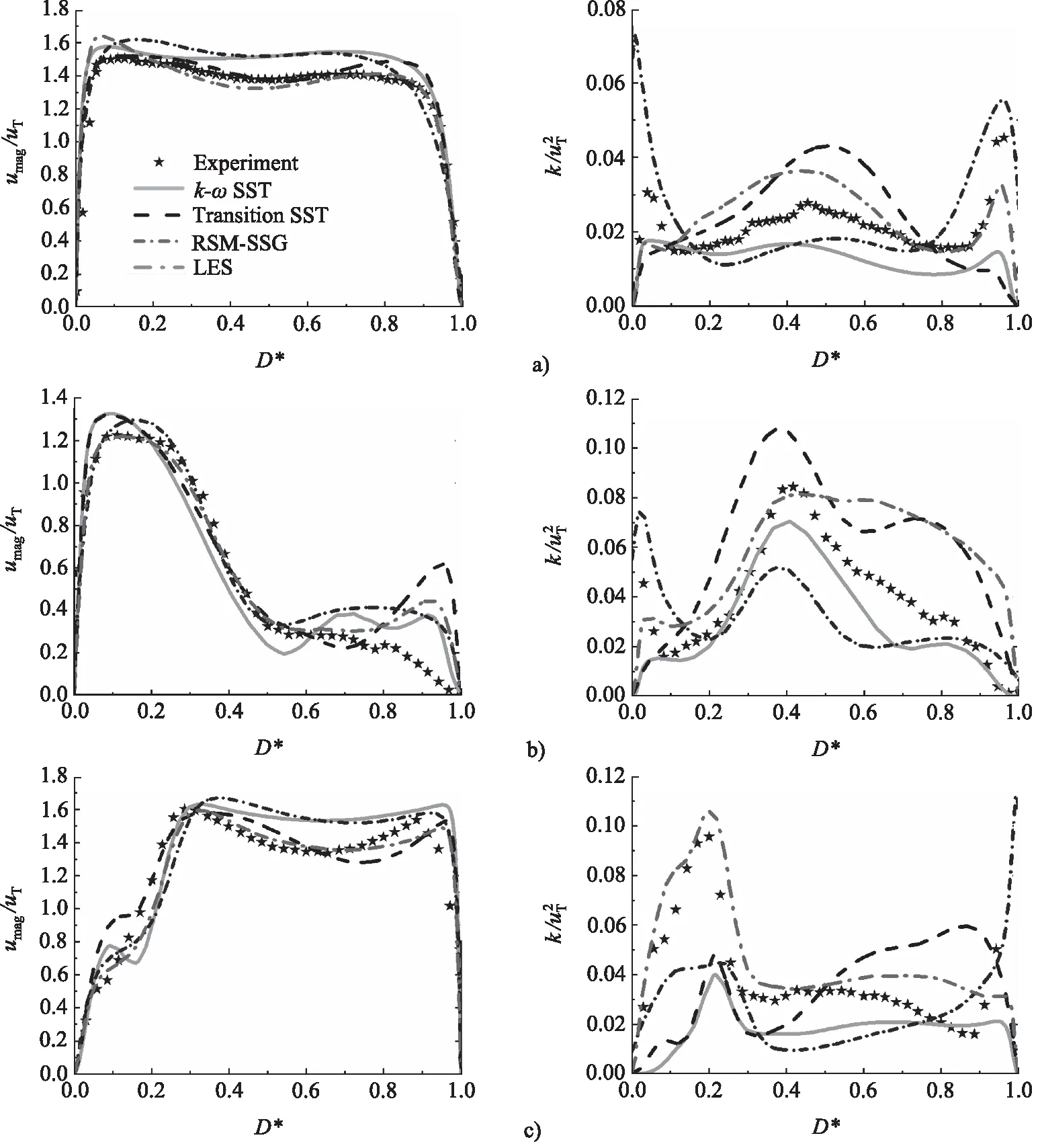
人體在不同的運動狀態或健康狀態下,呼吸速率和呼吸量會有較大的差別。根據吸入氣體的速度是否恒定(吸入速度是否隨時間變化,吸入速度不隨時間變化為穩態呼吸,反之),可以將呼吸狀態分為穩態呼吸和非穩態呼吸。本研究主要研究在穩定呼吸狀態下持續吸入0.5 s的過程,即Q(t) = 60 L/min,(0 表2 吸入流量Q=31.1 L/min時,10個出口的流速 表3 仿真邊界條件和數值方法設置 圖3 實驗裝置:模型的進氣管和口腔完全浸沒于裝有水-甘油混合液體的玻璃水箱中,模型的10個出口置于水箱下部并分別與10個活塞隔膜泵連接[29]。 圖4顯示了當t=0.5 s時,采用LES算法得到的進氣口到其中一個支氣管出口在呼吸道冠狀面和矢狀面上的時間平均流速分布(仿真中每10個時間步長求一次平均作為該時間區間內的時間平均值)。其中Ⅰ,Ⅱ,Ⅲ和Ⅳ分別表示口腔和氣管的矢狀面、氣管分叉處的冠狀面、左主支氣管的冠狀面和右主支氣管的冠狀面的具體位置。線段A,B,C,D,G,H和J分別表示支氣管樹內矢狀面或冠狀面上的截線。由圖4可知,隨著支氣管橫截面面積逐漸減小,氣流速度逐漸增大。每個支氣管分叉處的速度變化最為劇烈,會出現較為明顯的剪切層和回旋流區。為了更詳細的對比不同湍流模型計算結果的差異,取t=0.5 s這一時刻點的相關云圖和數據(不再贅述),對支氣管樹的不同區域進行詳細分析。 圖4 通過LES模型計算得到的呼吸道內從進口到其中一個出口的冠狀面和矢狀面時間平均流速分布;A,B,C,D,G,H和J分別表示支氣管樹內冠狀面或矢狀面與相應位置處橫斷面的交線;Ⅰ,Ⅱ,Ⅲ和Ⅳ分別展示了口腔和氣管的矢狀面、氣管分叉處的冠狀面、左主支氣管的冠狀面和右主支氣管的冠狀面的具體位置。 圖5a顯示了不同RANS湍流模型和LES模型在口腔和氣管矢狀面上的計算得到的結果。該處支氣管橫截面面積較大,氣體流動較慢,雷諾數常在3000~5000。從圖5a中可看出,氣體經過口腔(交線B處)和咽部(交線C處)時速度較低,在口腔上壁出現了流動分離現象。由于咽喉收縮,氣體流經此處時速度突然增大,并伴隨著剪切流和回旋流。隨著氣管結構產生彎曲,呼吸道內部高速流從氣管后壁轉移到氣管前壁,并且在前壁產生了一個較小的速度分離區域,該現象在LES模型的仿真結果中較為明顯。氣管中段區域,LES模型仿真計算的速度從氣管前壁到氣管后壁過渡的較為均勻。k-ωSST模型的計算結果和RSM-SSG模型的計算結果較為一致。在Transition SST模型的仿真中,并沒有在靠近氣管前壁面區域產生較大的流速,流速最大處主要集中在氣管中部。 對于上呼吸道內部的流場,LES模型能夠捕捉到氣管內更詳細的剪切流和回旋流。不同RANS湍流模型得到的總體速度分布具有較好的一致性,但是在預測喉部的剪切層和回旋流時有較大的差異。k-ωSST模型與RSM-SSG模型在近壁面區域計算的結果與LES模型計算的結果吻合性較好。Transition SST的結果與LES的結果差異較大。這是由于口腔和氣管中常存在回旋流和自由剪切流,Transition SST轉捩流模型計算這些流動時效果不佳[32]。口腔和氣管的時間平均湍動能如圖5b所示,湍動能在入口處較小,隨著流動的發展,在口腔的上部開始升高。最大的湍動能水平位于喉部氣管前壁和喉部下游區域的氣管后壁。k-ωSST模型和RSM-SSG模型明顯低估了該區域的湍動能水平。 圖5 使用不同RANS湍流模型和LES模型在口腔和氣管矢狀面上的計算結果(t=0.5 s) 為了進一步對比結果,取圖4中上呼吸道中的A,B,C和D四條交線處的實驗測量值、不同RANS湍流模型計算結果和LES模型計算結果進行比較。為了處理數據方便和更直觀地對比各湍流模型計算結果與實驗的差異,在每條交線上平均取200個離散點并編號,進而提取各個點上的時間平均速度和時間平均湍動能并進行無量綱化,最后將編號進行歸一化處理,均映射到0~1范圍之內的區間上,下同,如圖6所示。圖中D*表示交線上點的歸一化坐標。umag和k分別表示仿真得到的交線上的時間平均速度和時間平均湍動能。uT=2.28 m/s表示水-甘油混合液體在Q=31.1 L/min 時,進氣管橫截面的時間平均速度。4種湍流模型在交線A處得到的速度分布曲線較為一致,但與實驗有明顯差異。原因是實驗在裝滿水-甘油混合液體的水箱中進行的,水箱體積有限、壁面離進氣口較近等因素對實驗結果影響較大[15],從而使得入口處速度不對稱。氣體進入口腔后,所有湍流模型在B處均計算出了剪切流。隨著流動進一步發展,剪切層逐漸轉移到上咽(交線C處)內側,Transition SST模型的結果和RSM-SSG模型的結果與實驗結果更為吻合。交線D處的呼吸道橫截面突然增大,速度變化較為劇烈,四種模型得到的速度曲線與實驗結果具有較高的一致性,但是均不能精確的捕捉到剪切層的位置,其中Transition SST的表現最為不佳。 圖6 使用不同RANS湍流模型和LES模型在A,B,C和D四條交線處計算得到的無量綱化時間平均速度曲線(左圖)和無量綱化時間平均湍動能曲線(右圖)(t=0.5 s);a),b),c)和d)分別表示A,B,C和D四條交線;D*表示交線上點的歸一化坐標;umag和k分別表示仿真得到的交線上的時間平均速度和時間平均湍動能;uT=2.28 m/s表示水-甘油混合液體在Q=31.1 L/min時,進氣管橫截面的時間平均速度 與時均平均速度場相比,各個模型計算的湍動能明顯不同。在進氣管處,LES模型低估了湍動能水平,而k-ωSST、 Transition SST和RSM-SSG模型在進氣管中心區域得到地湍動能與實驗結果較吻合。其中,RSM-SSG模型在近壁面處捕捉到了較大的湍動能,這是由于仿真設置的進口邊界條件為大氣壓力,與進口周圍靜態環境相比進器管口產生較大的速度變化,從而表現出更高的湍動能。在B,C和D三條交線處,LES和Transition SST模型得到的湍流強度較為接近,能夠捕捉到湍動能的整體分布和大小。k-ωSST模型和RSM-SSG模型得到的湍流強度均低于實驗。RSM-SSG模型計算的湍動能沿著氣管衰減最快,但其仍能夠在近壁面捕捉到與實驗更接近的湍流強度。 隨著氣流進入左右支氣管,氣管分叉處和左右主支氣管(結構特征由人體生物學定義)的時間平均速度分布云圖如圖7所示。在Lizal[26]的體外測量實驗中,左肺和右肺的通氣量之比為3∶7,這種不相等的通氣量導致流速在氣管分叉處的左右區域差異巨大。在氣管的右壁處可以看到一個高速流動區域,此處的雷諾數能達到6000以上,而左側分叉處出現了一個較大的回旋流區域。隨著左主支氣管下游變窄和變短,流速逐漸增大,該區域產生了較大的剪切流區域。右主支氣管與下一級支氣管分支角度較大,這種幾何形狀的不對稱導致右主支氣管內出現射流現象。 圖7 使用不同RANS湍流模型和LES模型計算得到的時間平均速度場(t=0.5 s) 氣管分叉處和左右主支氣管的湍動能云圖如8所示,盡管湍流強度在氣管中出現了衰減,但是在剪切流和回旋流區域之間出現了較高的湍流水平,最大的湍流強度出現在右主支氣管。LES和Transition SST模型均能夠較好計算出左右主支氣管處的湍動能大小,k-ωSST模型和RSM-SSG模型依舊低估了此處的湍動能水平。如上所述,RSM-SSG雖然不能準確預測呼吸道中心區域的湍流水平,但是在近壁面處能夠捕捉到與實驗較為吻合的湍流強度。 圖8 使用不同RANS湍流模型和LES模型計算的時間平均湍動能場(t=0.5 s) 圖9顯示了G,H和J三條交線處的無量綱化的時間平均速度和時間平均湍動能曲線,在G處可以發現,LES模型計算的結果和實驗測量結果具有更好的一致性,Transition SST模型得到的結果與LES計算的結果最為接近。k-ωSST和RSM-SSG模型在此處的仿真結果均略高于實驗結果。隨著氣流進入左右主支氣管,氣管內開始出現了較為強烈的剪切流動,LES模型的計算結果與實驗測量結果最為接近。湍動能方面,LES模型與Transition SST模型在G處計算得到的湍動能分布與實驗較為一致,二者均能捕捉到此處湍動能的最大值和最小值。k-ωSST模型和RSM-SSG模型依舊低估了呼吸道中心處的湍動能水平,但是RSM-SSG仍然能很好的捕捉到近壁面的湍流強度。綜合比較三處交線的湍動能曲線可以發現,LES計算低級支氣管處的湍動能具有很大的優勢,其計算的湍動能與實驗測量值保持較高的一致性。k-ωSST模型在H處計算的湍動能與LES模型的結果最接近,Transition SST模型和RSM-SSG模型計算的湍動能與實驗結果的吻合度較低。 圖9 使用不同RANS湍流模型和LES模型在交線G,H和J三處計算的無量綱化時間平均速度曲線(左圖)和無量綱化時間平均湍動能曲線(右圖)(t=0.5 s);a),b)和c)分別表示G,H和J三條截線;D*表示橫坐標歸一化區間;umag和k分別表示仿真得到的截線上的時間平均速度和時間平均湍動能;uT=2.28 m/s表示水-甘油混合液體在Q=31.1 L/min時,進氣管橫截面的時間平均速度。 本研究使用真實人體呼吸道模型,采用全結構化網格劃分支氣管樹,并分別使用k-ωSST模型、Transition SST、雷諾應力模型(RSM-SSG)和大渦模擬(LES)計算呼吸道流場,通過與實驗測量結果比較發現: (1) 采用結構化網格劃分支氣管樹能夠極大的降低網格數量,進而可有效提升計算效率。 (2) 在上呼吸道區域,由于上呼吸道的橫截面面積較大,氣流在此處的流動處于發展階段,雷諾數相對較低。使用不同湍流模型在該區域計算得到的速度場中,Transition SST模型在流動混合區域的計算與實驗結果存在差異,k-ωSST模型、雷諾應力模型(RSM-SSG)和大渦模擬(LES)的計算結果與實驗結果的吻合度較高。在該區域湍動能場計算結果的比較中發現,LES不僅能較為準確地預測湍動能的分布狀態,而且能捕捉到喉部下游的湍流細節;Transition SST模型雖在預測近壁面湍動能時表現欠佳,但在預測呼吸道中心區域的湍動能水平時與LES最接近;k-ωSST和RSM-SSG湍流模型的計算結果對湍動能的預測均低于實驗測量結果,但RSM-SSG模型在近壁面處的湍動能計算結果與實驗保持一致。由于藥物顆粒的湍流擴散沉積主要與近壁面湍流場計算精度相關,因此RSM-SSG的計算結果是可接受的。 (3) 在支氣管區域,由于該區域的速度變化劇烈,常伴隨較強的剪切流和回旋流,雷諾數相對較高。LES和RSM-SSG在該區域的流動狀態和湍動能計算結果與實驗結果的差異較小。k-ωSST和Transition SST在此區域的速度場計算結果與實驗測量結果較為接近,但近壁湍動能場計算結果與實驗結果差異較大。 綜上所述,在計算真實人體呼吸道內部流場時,LES的計算結果與實驗結果最為接近。但當受限于計算效率時,結合結構化網格的巨大優勢,使用RSM-SSG模型代替LES模型,可以有效節約計算時間,能夠最大程度的減小計算精度與LES模型的差異對顆粒湍流擴散沉積的影響,從而為計算流體力學仿真模擬大規模應用于呼吸道疾病的臨床應用提供參考和奠定基礎。 致謝 作者十分感謝科技部國際合作司中國與斯洛文尼亞科技人員交流項目對該研究的支持,以及COST (European Cooperation in Science and Technology; Simulation and pharmaceutical technologies for advanced patient-tailored inhaled medicines; www.cost.eu)對本研究提供的幫助。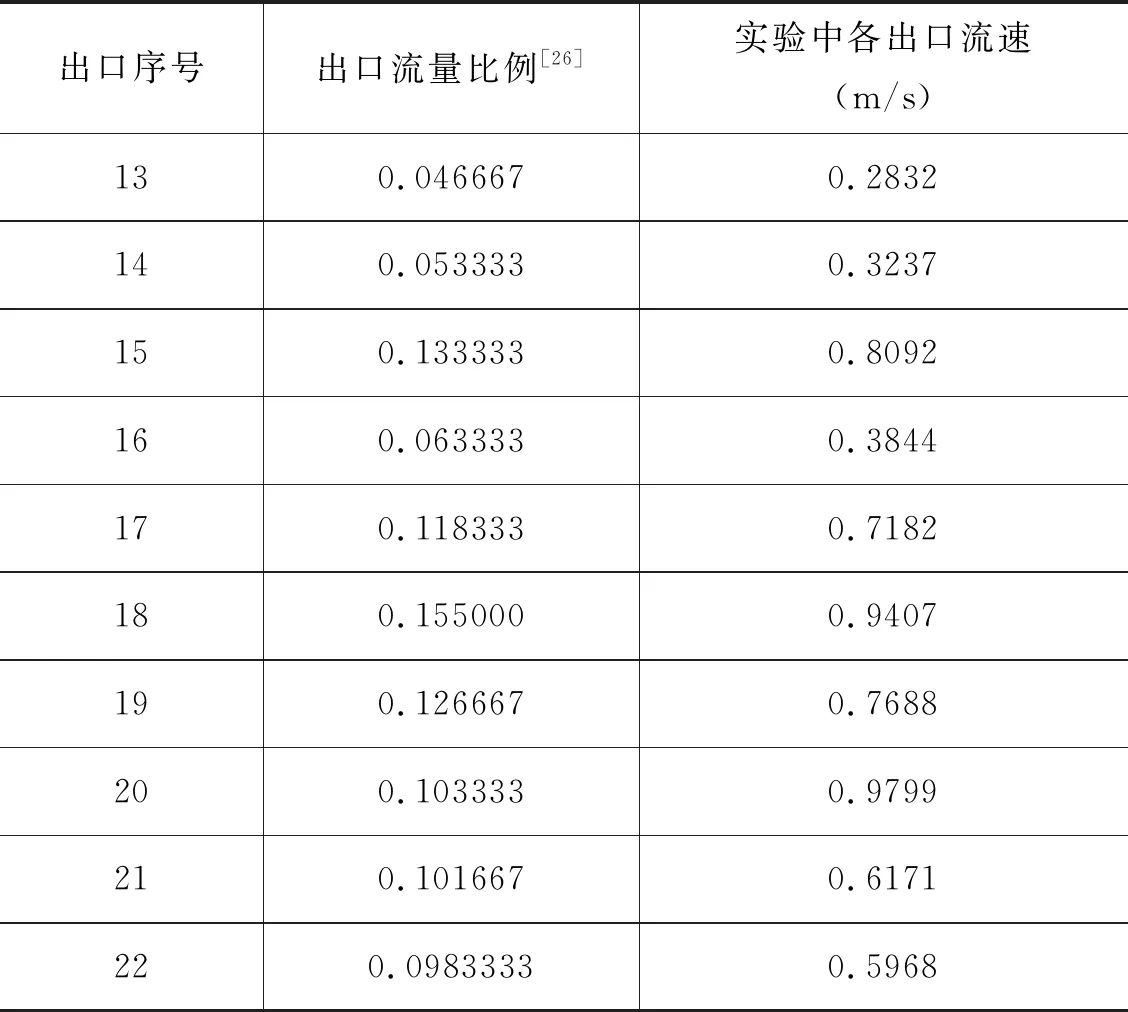
3 計算結果與分析

4 結論

