基于多智能體深度強化學習的空間眾包任務分配
趙鵬程, 高 尚, 于洪梅
(吉林大學 計算機科學與技術學院, 長春 130012)
眾包(crowdsourcing)是一種利用人群智慧完成任務的計算范式. 隨著移動互聯網的快速發展和移動設備的普及, 空間眾包(space crowdsourcing, SC)[1]成為一種新興的眾包類別. 在SC系統中, 首先請求者將時空任務提交到平臺; 然后在差旅預算、 任務期限和技能要求等約束條件下進行任務分配或選擇; 最后工人在截止日期前趕往指定地點完成任務并獲得報酬. 目前, 任務分配作為空間眾包中最基本的挑戰, 得到廣泛關注. 現有的工作存在以下不足: 1) 大多數只考慮工人或請求者單方面的利益, 若只考慮工人利益, 則會導致偏遠地區的任務難以完成; 若只考慮請求者利益, 則任務分配可能會對某些工人不公平; 2) 通常只考慮強制工人合作或禁止工人合作的單一場景, 前者忽略了工人的情感和偏好, 而后者不利于工人和請求者利益的最大化; 3) 精確算法由于復雜度過高而難以在實際中應用, 而貪婪算法僅注重眼前利益, 只能得到次優解.
研究表明, 多智能體系統(multi-agent system, MAS)與眾包系統的關鍵要素和過程聯系緊密[2], 多主體技術可用來提高眾包系統的自適應性和自組織性, 并解決任務分配、 任務分解、 激勵機制設計等眾包中的典型挑戰. 此外, 深度強化學習(deep reinforcement learning, DRL)以Markov決策過程為理論框架, 考慮了動態環境下的即時回報和未來回報, 根據與復雜環境交互的經驗, 直接擬合參數化模型學習最優策略, 在許多復雜的實際問題中都取得了成功. 近年來, 研究者們開始將注意力機制[3-5]引入DRL模型中, 通過有針對性地利用輸入信息, 提升了模型的性能[6-7].
基于上述研究, 本文通過定義允許但非強制合作的空間眾包(allow but not force cooperation spatial crowdsourcing, ABNFC-SC)場景, 利用基于A2C(advantage actor-critic)方法的多智能體深度強化學習(multi-agent deep reinforcement learning, MADRL)模型解決其中的任務分配問題. 優化目標是同時最大化任務完成率和工人收益率, 且本文設計了同時考慮請求者利益和工人利益的全局獎勵函數. 為提升模型的性能, 引入注意力機制以指導智能體間的協作. 實驗結果證明了本文方法的有效性、 魯棒性和優越性.
1 預備知識
1.1 多智能體深度強化學習與A2C算法
多智能體強化學習是強化學習的思想和算法在多智能體系統中的應用[8-9], 其中各智能體在與環境互動和彼此交流中不斷地學習和改進自身策略, 所有智能體協同工作以實現特定的目標[10]. 為解決更大規模和更高復雜度的問題, 研究者們將深度學習方法[11-12]與傳統的多智能體強化學習算法相結合, 提出了多智能體深度強化學習.
演員-評論家(actor-critic, AC)算法是經典的強化學習方法, 該方法訓練一個充當Actor角色的策略網絡以產生最優化策略, 同時訓練一個充當Critic的價值網絡對Actor的動作進行打分, 并指導Actor的策略更新. 通過引入優勢函數, 可得AC方法擴展為A2C方法[13], 實現了性能的進一步提升.
1.2 注意力機制
注意力機制的原理是通過訓練參數化模型從輸入信息中提取出與任務目標高度相關的信息, 排除干擾, 從而提高任務處理的效率和準確性. 本文采用經典Query-Key-Value模式的注意力機制[14], 其形式化描述為
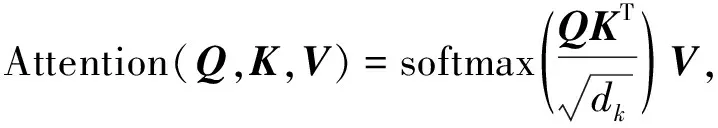
(1)
其中Q,K,V為特征向量,dk為Q(或K)的維度.
2 場景定義
本文所用的一些符號及其意義列于表1.

表1 符號及描述
2.1 任務和工人
在每個時間步, 任意任務tj(j∈[1,M])都可定義為一個七元組tj=〈l,a,d,b,r,f,Ψ〉, 其中:tj.l表示任務所在位置;tj.a表示任務被提交到平臺的時刻;tj.d表示任務的截止時間;tj.b表示任務預算;tj.r表示任務半徑, 即平臺只為tj分配位于以tj.l為圓心、 以tj.r為半徑范圍內的工人;tj.f表示任務是否允許被多個工人合作完成,tj.f=1表示允許,tj.f=0表示禁止; 向量tj.Ψ=(ψ1,ψ2,…,ψNΨ)標記了任務的技能要求, 其中NΨ為所有任務要求技能的總數, 并且對?k∈[1,NΨ],tj.Ψ.ψk=1表示tj要求對應技能,tj.Ψ.ψk=0表示tj不要求對應技能.
在每個時間步, 任意工人wi(i∈[1,N])都可以定義為一個六元組wi=〈l,v,ξ,f,μ,Ψ〉, 其中:wi.l表示工人的當前位置;wi.v表示工人的移動速度;wi.ξ表示工人在前往任務地點行程中單位距離的開銷;wi.f表示工人是否愿意與他人合作,wi.f=1表示愿意,wi.f=0表示不愿意;wi.μ表示失敗概率, 即wi有wi.μ的概率使任務失敗(由于設備故障、 主觀放棄等原因); 與任務中的對應定義類似, 向量wi.Ψ=(ψ1,ψ2,…,ψNΨ)標記了wi擁有的技能.
2.2 技能覆蓋向量
為清楚表達工人wi對任務tj技能要求的滿足程度, 同時為方便描述, 下面給出技能覆蓋向量(skill cover vector)的概念, 其為一個NΨ維向量, 定義為

(2)
其中對?k∈[1,NΨ], 有
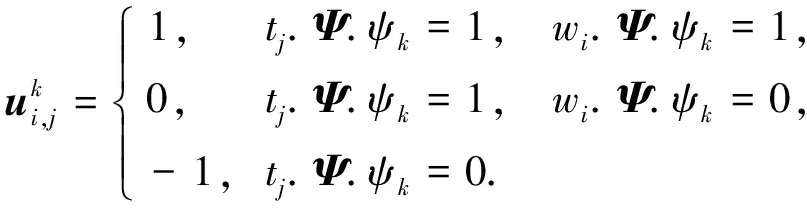
(3)
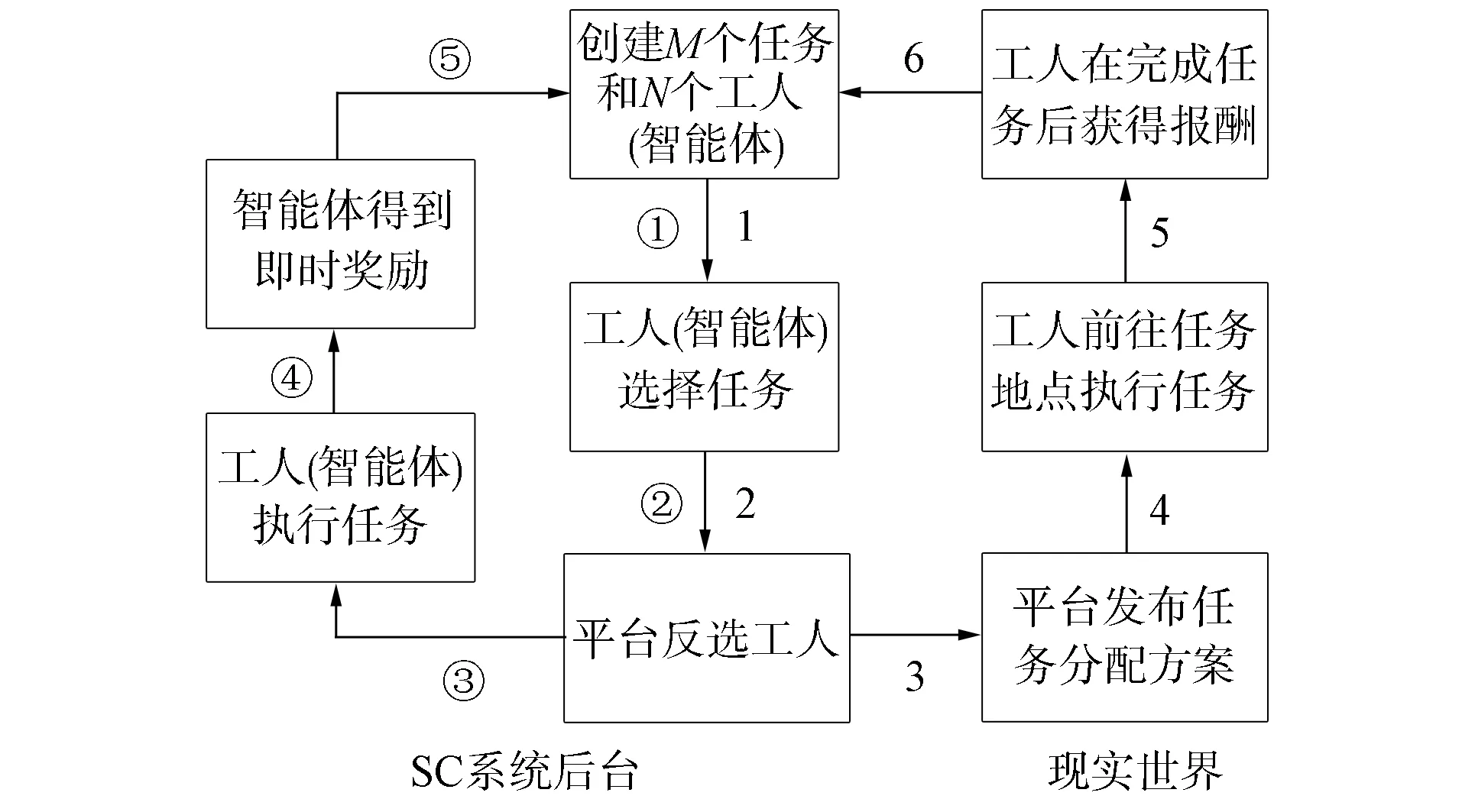
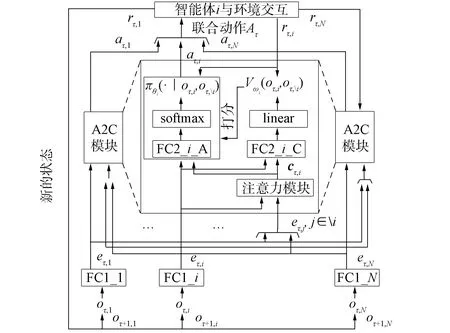
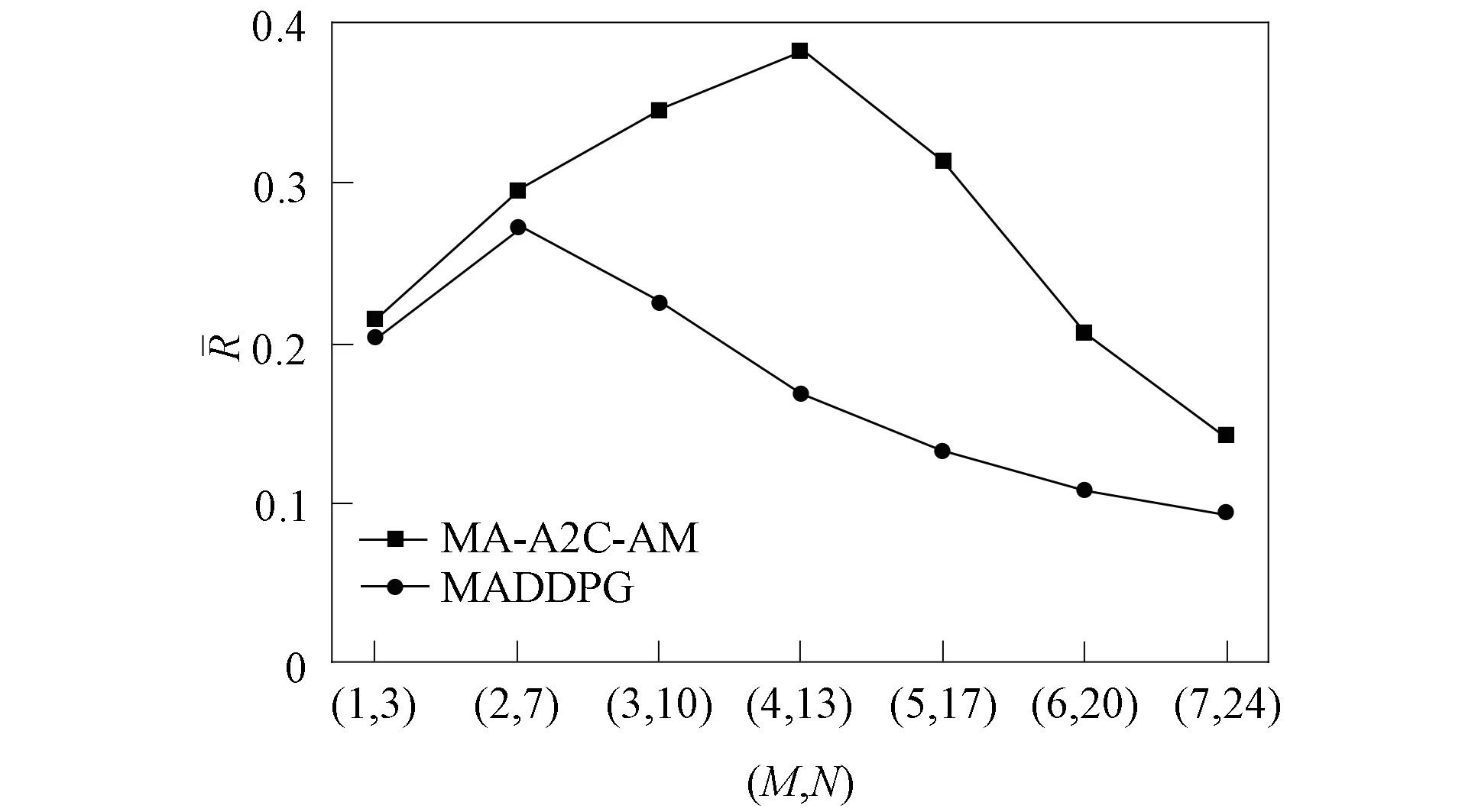
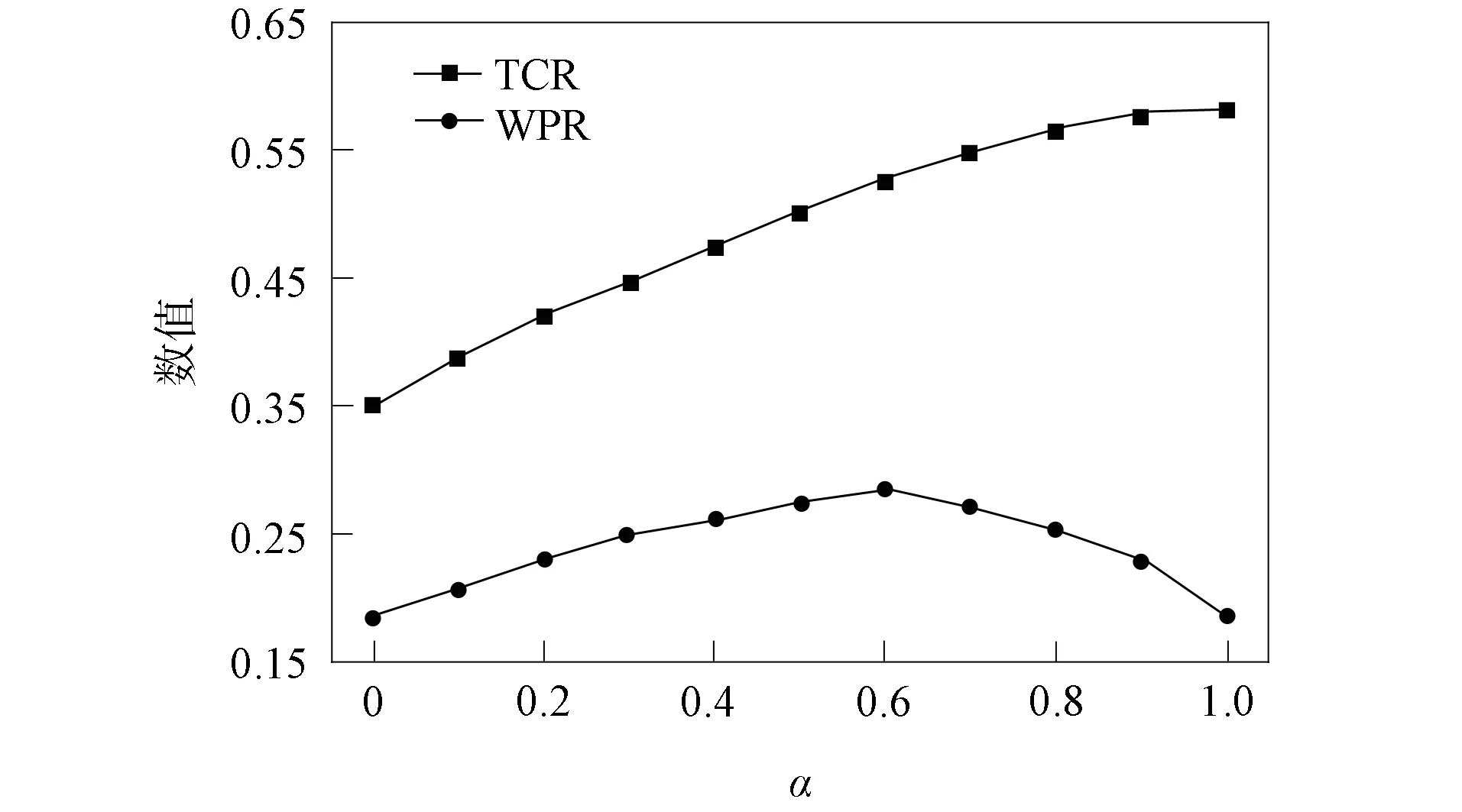
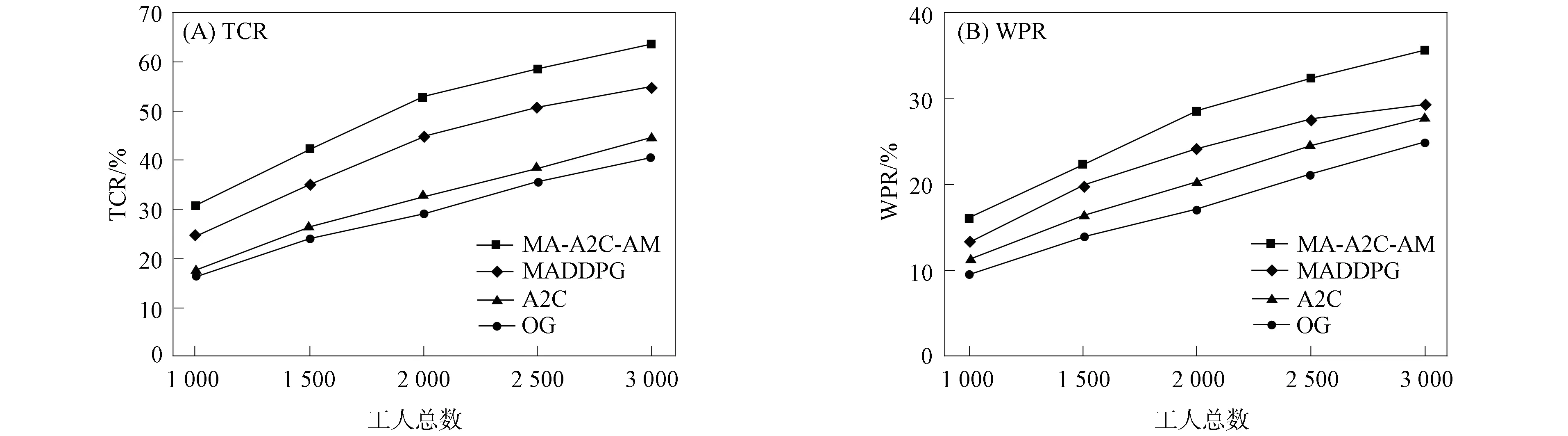
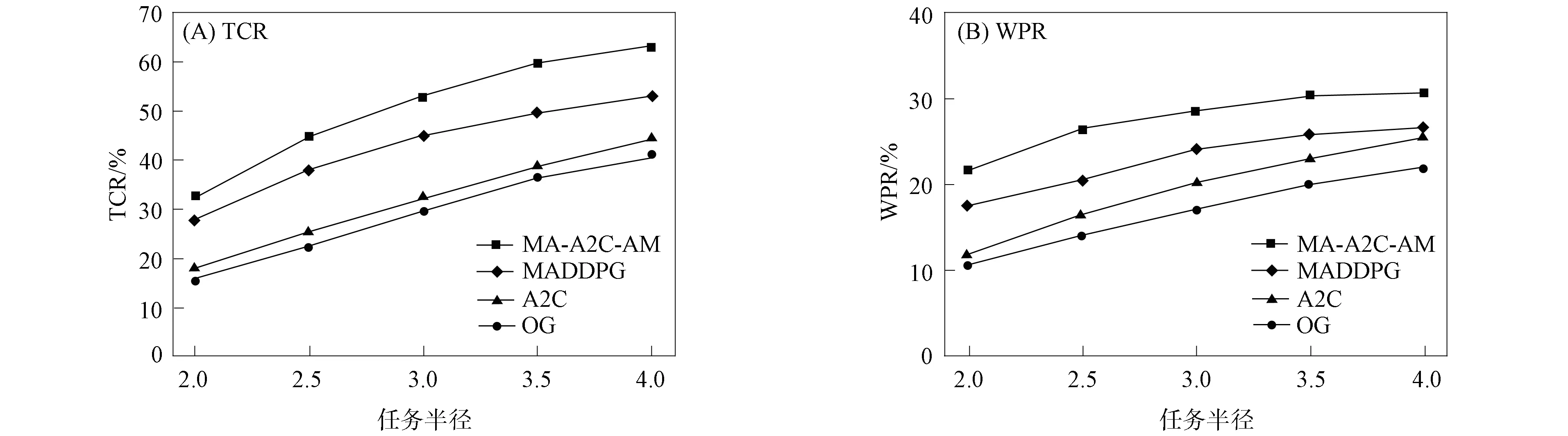
進一步, 為Up,j和Uq,j(0 (4) 下面給出wi成為tj的潛在工人的約束條件.潛在工人的含義:wi是tj的潛在分配對象, 但平臺最終不一定會將tj分配給wi.約束條件如下. 1) 空間約束:wi必須位于tj的選擇半徑內, 即 dist(wi.l,tj.l)≤tj.r, (5) 其中不等號左邊表示wi和tj之間的直線距離. 2) 時間約束:wi必須在tj的截止時間前到達任務地點, 即 route(wi.l,tj.l)/wi.v≤(tj.d-tj.a), (6) 其中不等號左邊表示從wi.l到tj.l的路線長度. 3) 預算約束:wi的行程代價不得超過任務預算, 即 Ci,j=wi.ξ·route(wi.l,tj.l)≤tj.b. (7) 4) 技能約束: 在tj有技能要求的前提下, 如果tj禁止合作或wi不愿合作, 則wi必須具備tj要求的全部技能; 否則,wi只需具備至少一項tj要求的技能即可, 即 (8) 其中ones表示求向量中1的個數的函數. 基于上述條件, 定義參數Fi,j, 規定若wi和tj滿足上述條件, 則Fi,j=1, 表示wi是tj的潛在工人; 反之,Fi,j=0, 表示wi不是tj的潛在工人. 下面給出由潛在工人組成的工人小組G可獲得tj的必要條件. 1) 整體預算約束: 小組成員的行程代價之和不得超過任務預算, 即 (9) 2) 整體技能須滿足tj的技能要求, 即令 UG=U1,j⊕U2,j⊕…⊕U|G|,j, (10) 則 ones(UG)=ones(tj.Ψ). (11) 特別地, 當|G|=1時, 上述條件即為單個潛在工人可獲得tj的必要條件. 本文將每個工人建模為一個智能體, 但MADRL模型中智能體的個數和網絡結構都是固定的, 因此MADRL只支持在固定個數的工人和任務之間進行匹配(設任務和工人的個數分別為M,N), 而現實中M個任務不一定恰好對應N個潛在工人.本文采用如下方法解決該問題: 在每輪匹配中, 首先利用下列每輪匹配中任務和工人選擇算法確定實際參與匹配的工人集合W和任務集合T; 其次, 若|W| 算法1每輪匹配中任務和工人選擇算法. 輸入:M,N, 任務隊列Qt, 可用工人集合SW, 計數器k; 輸出: 參與本輪匹配的任務集合T和工人集合W; 1) 初始化:T=?,W=?,k=0 2) while TRUE 3)t←Qt.top( ) 4)G←GetPotentialWorkers(t,SW)//由約束條件, 從SW中找出t的所有潛在工人, 構成集合G 5) ifk+1≤M, |W∪G|≤Nthen 6)k←k+1,W←W∪G,T←T∪{t},Qt.pop( ),SW←SW-G 7) else 8) break 9) end if 10) end while. 圖1 ABNFC-SC工作流程Fig.1 Workflow of ABNFC-SC 本文解決方案的思路如圖1所示, 首先在訓練階段的每個時間步, 根據算法1, 由訓練數據生成M個任務和N個工人/智能體(其中可能包含虛擬的任務或工人), 并由每個智能體根據自身的策略選擇要執行的任務. 工人選擇好任務后, 進入任務反選工人過程, 即對每個任務, 根據約束條件, 通過窮舉搜索, 在選擇了該任務的工人中選出能以最小代價完成該任務的工人或工人小組(如果存在這樣的工人或工人小組). 然后程序模擬工人執行任務的過程, 并根據執行結果計算各智能體的立即回報. 最后, 根據立即回報更新MADRL模型參數并開始下一輪匹配. 重復以上過程直到訓練結束. 注意, 盡管窮舉搜索的復雜度較高, 但在本文研究的問題中, 選擇同一任務的工人一般不超過5個, 因此窮舉搜索是完全可行的. 在實際應用階段, 任務被提交到平臺后先進入任務隊列等待, 當平臺上等待的任務數量和對應的潛在工人數量達到匹配條件(即算法1中循環的退出條件)時, 平臺即進行一次任務分配. 首先, 由訓練好的MADRL模型在后臺模擬工人選擇任務; 然后, 運用窮舉搜索, 平臺反選工人并形成最終的任務分配方案發布; 最后, 獲得任務的工人前往任務地點執行任務并取得報酬. 圖2 MA-A2C-AM架構Fig.2 Architecture of MA-A2C-AM 本文提出具有注意力機制的多智能體優勢演員-評論家(multi-agent advantage actor critic with attention mechanism)模型, 簡稱MA-A2C-AM, 其架構如圖2所示. 為解決可擴展性問題, 本文采用去中心化結構; 為解決環境非穩定問題, 本文利用注意力機制計算其他智能體對智能體i的影響ci, 并將ci和局部觀測oi一起輸入價值網絡Vωi, 使得Critic能根據局部觀測和來自其他智能體的有效信息更準確地評估當前狀態. 進一步, 本文同時將ci引入策略網絡πθi, 使智能體學會彼此合作, 根據其他智能體的狀態自適應地調整自身策略, 最終實現整體利益的最大化.圖2中, i表示除智能體i外其他智能體的集合. 首先定義智能體i的局部觀測oi為 oi={wi.f,Ii,1,Ii,2,…,Ii,M}, (12) 其中對?j∈[1,M], 向量Ii,j表示與tj相關的信息, 表示為 Ii,j=(tj.f,tj.b,Fi,j,Ci,j,Ui,j), (13) 式中Ci,j為從wi.l到tj.l的行程代價.對智能體i, 其策略網絡和價值網絡的輸入均為其局部觀測oi和其他智能體信息對它的影響, 即由注意力機制計算出的上下文向量ci. 策略網絡的輸出是一個概率分布, 輸出節點有(M+1)個, 其中前M個節點的輸出值依次表示選擇任務t1到任務tM的概率, 第(M+1)個節點的輸出表示不選擇任何任務的概率.價值網絡只有一個輸出節點, 其輸出是一個實數, 表示對智能體i當前狀態的打分, 即對智能體i在當前狀態下的折扣累計回報估計. 在ABNFC-SC中, 工人之間本質上是相互協作的關系, 需要相互協作以完成共同的目標----最大化任務的完成率和工人的整體收益. 因此, 本文將獎勵函數設置為任務完成率和工人收益率的加權和, 且所有智能體共享此獎勵, 即對任意?i∈[1,N], 智能體i在時間步τ的即時獎勵為 (14) 其中α∈[0,1]為權重參數,Tτ和Mτ分別為第τ個時間步發布和完成的實際任務總數,Vτ為第τ個時間步發布的實際任務總價值(即預算之和),Pτ為第τ個時間步工人的總收益(即工人完成的任務總價值減去工人總的行程代價).這些量都可以在訓練過程中根據工人執行任務情況及任務和工人的屬性計算. 在時間步τ, 對任意智能體i, 首先用全連接層FC1_i對局部觀測oi進行embedding操作, 得到ei.其次, 利用注意力機制由ei和ek(k∈i)計算出上下文向量ci, 然后將ei和ci輸入第二個全連接層FC2_i_A和FC2_i_C, 再分別經過softmax層和linear層得到最終的策略和對當前狀態的打分.最后, 根據策略產生動作aτ,i, 以所有智能體的聯合動作Aτ=aτ,1×aτ,2×…×aτ,N與環境互動, 從而得到即時獎勵rτ,i和新的觀測oτ,i+1, 并進入下一輪迭代.期間, 智能體會收集軌跡數據并適時更新網絡參數. 本文將策略網絡的損失函數定義為 (15) 其中:τb和τe分別表示minibatch中的第一個和最后一個時間步;Aτ,i為優勢函數, (16) γ∈(0,1]為折扣因子.式(15)同時包含了策略梯度損失和策略熵損失.策略梯度損失的作用是根據優勢函數的正負增大或減小在未來采取相應動作的概率, 而引入策略熵損失的目的是鼓勵智能體在訓練初期多探索不同動作, 避免模型短期內貪婪地收斂到局部最優.超參數β通常是一個很小的正數, 用于確定熵項的相對重要性. 為提高價值網絡對當前狀態下預期回報的評估準確性, 本文將折扣累計回報和價值網絡輸出之間的均方誤差作為價值網絡的損失函數, 即 (17) 算法2MA-A2C-AM訓練過程. 輸入: 每個智能體的價值網絡和策略網絡; 輸出: 網絡參數{θi}i∈[1,N],{ωi}i∈[1,N]; 超參數:α,β,γ,|B|,T,ηθ,ηω//T表示訓練的總步數; 2) repeat 3) 對?i∈[1,N]: 智能體i根據πθi(·|oτ,i,oτ,i)執行動作aτ,i 4) 用聯合動作Aτ=aτ,1×aτ,2×…×aτ,N與環境互動, 模擬工人執行任務 5) 對?i∈[1,N]: 智能體i得到獎勵rτ,i和新的局部觀測oτ+1,i 6) 對?i∈[1,N]:Bi←Bi∪{(τ,oτ,i,aτ,i,rτ,i,oτ+1,i,oτ+1,i)} 7)h←h+1,τ←τ+1,k←k+1 8) ifk=|B| or訓練數據耗盡 9) 對?i∈[1,N]: 對?τ∈Bi, 計算Rτ,i;θi←θi-ηθθiL(θi);ωi←ωi-ηωωiL(ωi);Bi←? 10)k←0 11) end if 12) if 訓練數據耗盡 13)τ←0,k←0, {Bi←?,o0,i}i∈[1,N] 14) end if 15) untilh≥T. 算法2給出了模型的訓練過程. 在時間步τ, 首先對?i∈[1,N], 智能體i根據局部觀測和策略網絡選擇動作ai.然后程序模擬聯合動作與環境的交互并計算即時獎勵rτ,i, 同時每個智能體收集自身訓練軌跡.當樣本的數量達到minibatch規模或訓練數據耗盡時, 每個智能體根據樣本和價值網絡計算折扣累計回報Rτ,i, 并通過小批量梯度更新策略網絡和價值網絡的參數. 如果訓練數據耗盡但未達到總訓練步數, 則使用原訓練數據開始新一輪訓練. 迭代以上訓練過程, 直到達到總訓練步數. 本文將MA-A2C-AM與MADDPG[15],A2C[13],OG[16](online greedy)等3種方法進行性能比較. 其中: MADDPG是經典的多智能體深度強化學習方法, 采用集中訓練分散執行架構, Actor僅依據局部觀測做出決策, 而集中式Critic根據所有智能體的觀測為Actor打分, 在本文實驗中, MADDPG的工作方式與MA-A2C-AM完全相同, 區別僅在于兩者采用不同的強化學習模型產生策略; A2C是經典的單智能體強化學習方法, 同樣采用Actor-Critic架構, 并利用優勢函數降低估計的方差, 本文中A2C采用在線分配方法, 為每個新到達的任務選擇合適的工人; A2C無法支持工人合作, 因為在合作場景下單智能體強化學習的動作空間隨潛在工人數量呈指數增長; OG是一種在線貪婪算法, 其迭代地嘗試將能以較低的成本覆蓋更多技能的工人分配給當前任務, 直到完成任務. 所有基于強化學習的方法均使用式(14)作為回報函數. 本文使用任務完成率(task completion rate, TCR)和工人收益率(worker profitability rate, WPR)兩項指標評價各算法的性能, 分別表示為 (18) (19) 表2 實驗場景設置 本文將2013-01-01—2018-12-31的數據, 共1 778 108條, 用于訓練, 剩余700 466條數據用于測試. Actor和Critic被同時訓練, 以形成最佳任務分配策略, 但在測試時只需使用Actor產生動作, Critic被棄用. MA-A2C-AM,MADDPG和A2C均采用Leaky ReLU為激活函數, Adam為梯度優化器, 神經網絡的權重和偏置均由機器學習庫PyTorch默認初始化. 超參數β和γ統一設置為β=0.01,γ=0.98, 所有模型均訓練100萬時間步. 對MA-A2C-AM, FC1_i及注意力模塊中的全連接層節點個數為24, FC2_i_A和FC2_i_C節點個數為64. 對MADDPG, Actor隱藏層設置為{32,16}, Critic隱藏層設置為{128,64,32}. 為增加早期探索,ε-greedy被用作行為策略, 且在訓練的前3/4段,ε從0.8指數衰減到0.01.對于A2C, 其價值網絡和策略網絡隱藏層均為{64,32}, 并且任務的潛在工人上限設為5, 即在每輪匹配中, 若當前任務的潛在工人不足5位, 則以虛擬工人補充; 若超過5位(實驗中該情況極少發生), 則選最先找到的5位. 其余超參數及訓練時長列于表3, 其中訓練時長取多次相同實驗的平均值. 表3中, lr_a和lr_c分別表示Actor和Critic的學習率. 實驗的軟硬件設置為: 系統采用Ubuntu 16.04 LTS, 編程語言采用Python 3.7.4+PyTorch 1.0.0, CPU為Intel Xeon E5-2620×1, GPU為Tesla P40×1. 表3 超參數和訓練時長 本文采用控制變量法進行實驗, 可變參數為工人總數、 任務半徑、 任務預算, 其取值見表2. 其中U(2.1,25),3.0,2 000表示默認值. 在每組實驗中, 只改變其中一個參數, 同時保持其他參數為默認值. 在進行對比實驗前, 需確定不同實驗條件下M,N,α的最佳取值. 4.3.1 確定最佳M,N值 由于訓練強化學習模型會耗費大量時間, 所以通過枚舉(M,N)并進行大量實驗確定所有實驗條件下的最佳(M,N)不切實際, 因此本文結合有限的實驗推斷不同條件下(M,N)的合理取值.步驟如下: 1) 在表2所列的默認實驗條件下, 取α=0.5, 對某特定M, 依次取M個連續的任務并根據算法1計算對應的潛在工人數量, 記為NM, 可得一系列NM.對這些NM求平均值并對結果取整, 將最終的結果記為N, 即得到了一個(M,N)對, 改變M, 最終得到一系列的(M,N)對, 即{(1,3),(2,7),(3,10),(4,13),(5,17),(6,20),(7,24)}. 3) 對于其他實驗設置, 首先按步驟1)中的方法找出對應的(M,N)對, 然后選出N值位于步驟2)中最優區間中的(M,N)對, 如果有多個(M,N)對符合條件, 則將N值最小的(M,N)對作為最終結果.表4列出了不同可變參數下最終選定的(M,N)對. 4.3.2 確定最佳α值 為找到最合適的比例系數α, 本文考察了MA-A2C-AM針對不同α的表現.令α在0~1間以0.1為步長變化, 其余參數采用默認值, 觀察MA-A2C-AM在TCR和WPR兩個指標上的變化, 結果如圖4所示.由圖4可見, 當α>0.6時, TCR的增加變得緩慢, 同時WPR開始下降, 所以實現整體最大化的α值在0.6附近.進一步的實驗證明,α對不同條件不敏感且MA-A2C-AM上的結論同樣適用于MADDPG.因此, 在后續實驗中統一設置α=0.6. 表4 不同實驗條件下的(M,N)對 圖3 (M,N)對對實驗結果的影響Fig.3 Effect of (M,N) pairs on experimental results 圖4 α對實驗結果的影響Fig.4 Effect of α on experimental results 4.3.3 結果對比 確定了最佳的(M,N)和α后, 下面將MA-A2C-AM與其他3種任務分配方法進行性能對比. 工人總數對實驗結果的影響如圖5所示. 圖5 工人總數對實驗結果的影響Fig.5 Effect of total number of workers on experimental results 由圖5可見, 隨著可用工人數量的增加, 所有方法都可以更好地實現分配. OG雖然允許工人合作, 但其只貪婪地優化當前任務的分配, 形成了局部最優解, 因而表現最差. 由于A2C無法支持工人間的合作, 因此難以實現較高的任務完成率, 在TCR上僅略優于OG. A2C在WPR上相對于OG有較明顯的優勢, 表明A2C學習到了有利于長期目標的策略. MADDPG和MA-A2C-AM優于另外兩種方法, 表明合作機制加上合理的分配策略, 能提高任務分配的效果, 也顯示出多智能體強化學習在解決空間眾包任務分配問題上的優勢. 去中心化的MA-A2C-AM比集中式訓練的MADDPG有更好的可擴展性, 可以在較多的任務和工人間進行匹配, 并且MA-A2C-AM中的注意力機制促進了智能體間的協作. 因此, MA-A2C-AM實現了優于MADDPG的分配策略. 圖6 任務半徑對實驗結果的影響Fig.6 Effect of task radius on experimental results 任務半徑對實驗結果的影響如圖6所示. 由圖6可見, 圖6中各方法的排名相對于圖5沒有變化. 隨著任務半徑的增大, 可用工人逐漸增多, 原來無法得到工人的任務可以被較遠地方的工人執行, 因此TCR和WPR隨之提高. 但距離越遠的工人行程代價越高, 其收益也越低, WPR的增速隨任務半徑的增大而逐漸放緩. 特別地, 對于MADDPG和MA-A2C-AM, 盡管兩者憑借較好的策略使更多的任務被工人合作完成, 但由于合作小組總的行程代價與小組規模成正比, 因此, 當任務半徑大于3.0 km時, 盡管兩者的TCR還略有增加, 但WPR卻幾乎不再增加. 任務預算對實驗結果的影響如圖7所示. 為簡單, 在圖7中, 任務預算區間用區間的左側表示. 由圖7可見, 不同方法的排名仍然沒有變化. 過低的預算通常不足以抵消工人的行程代價, 而當預算超過任務半徑內最昂貴的工人行程代價時, 即使再增加預算, 可用工人也不會再增加. 由圖7(A)可見, 當預算區間在[0.4,0.9]時, 所有方法均較差, 而當預算大于1.7時, 所有方法的TCR幾乎都不再增加. 而預算的增加直接導致了工人收益的增加, 因此圖7(B)中WPR能持續增長. 圖7 任務預算對實驗結果的影響Fig.7 Effect of task budget on experimental results 綜上所述, 針對目前空間眾包場景單一、 分配方法難以兼顧請求者和工人雙方利益的問題, 本文提出了一種基于多智能體深度強化學習的空間眾包任務分配算法. 首先形式化定義了允許但不強制工人合作的空間眾包場景, 然后設計了基于多智能體深度強化學習模型的分配算法. 為指導智能體間的有效合作, 引入了注意力機制; 為平衡請求者和工人雙方利益, 設計了同時考慮雙方利益的獎勵函數. 對比實驗結果表明, 本文方法均實現了最優的任務完成率和工人收益率, 證明了本文方法的可擴展性、 有效性和魯棒性.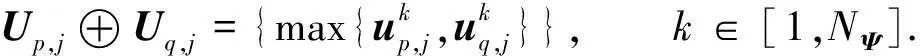
2.3 約束條件
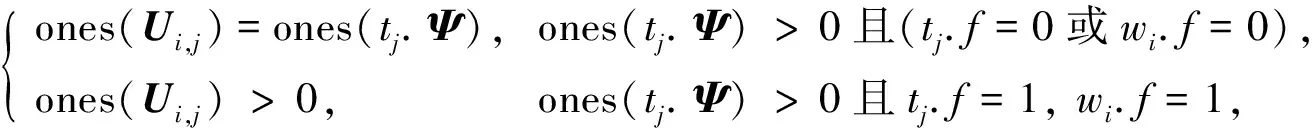
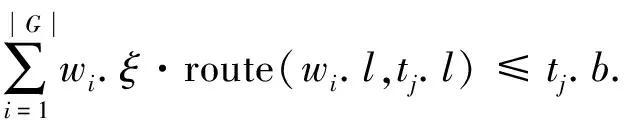
2.4 解決方案
3 模型設計
3.1 模型概述
3.2 輸入輸出和獎勵函數
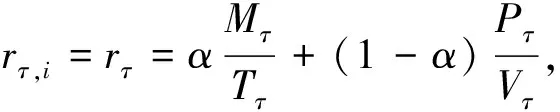
3.3 工作流程
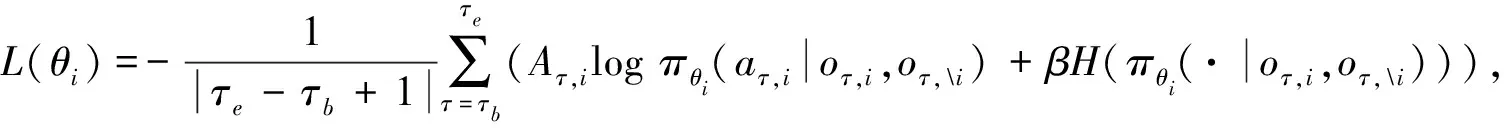
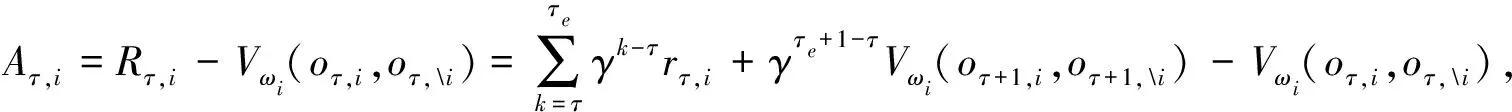
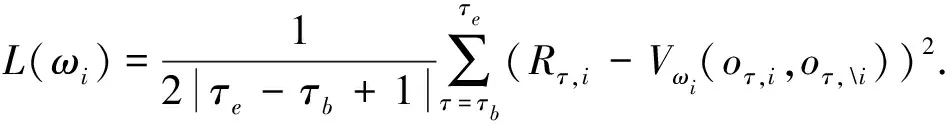
3.4 模型訓練
4 實驗分析
4.1 對比方法和評價指標


4.2 實驗數據和基本設置
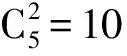


4.3 結果與分析
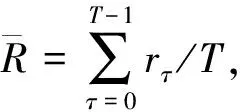

4.4 復雜度分析

