基于五桿支鏈性能優化和配置的并聯機器人設計方法研究

徐懷安，林松，江競宇

基于五桿支鏈性能優化和配置的并聯機器人設計方法研究

徐懷安，林松*，江競宇

（同濟大學 機械與能源工程學院，上海 201804）

隨著運動任務要求的多樣化和復雜化，傳統并聯機器人設計方法的不透明性和動平臺的不變性，導致設計結果會出現偏差且柔性化程度較低。因此提出一種基于五桿支鏈性能優化和配置的并聯機器人設計方法。首先利用解析和幾何法結合，完成五桿機構運動分析和奇異性分析，根據相關性能評價指標完成支鏈五桿的尺度綜合。之后，提出平面幾何投影法將要求工作空間投影到支鏈五桿的最佳工作區，綜合考慮工作空間及運動性能的需求，實現了并聯機器人的設計和配置，提高了設計透明度。

并聯機器人；支鏈五桿機構；尺度綜合；工作空間投影

并聯機器人是由若干個運動支鏈連接動平臺和定平臺組成的，一般具有兩個或兩個以上的自由度[1]，如Stewart平臺[2]、Delta機器人[3]、H4機器人[4]等。隨著應用和研究的不斷深入，并聯機器人也出現了諸多問題。在支鏈設計方面，現有并聯機器人多采用若干相同的開鏈結構，導致支鏈運動性能和力學性能較差，因此在支鏈機構中引入閉環結構成為提高并聯機器人性能的主要方法。劉辛軍等[5]分析了3-PUU并聯機構在某些位形會出現動平臺自由度增加的狀況，采用四桿閉環子鏈代替UU運動副，實現了機構運動傳遞的有效性。Gosselin[6]利用三條含平面五桿機構的支鏈設計了一種并聯機器人，實現了六自由度的調整。葉偉[7]將閉環五桿機構作為并聯機構的子鏈，實現了不同的可重構運動方案。可見，五桿機構已經作為支鏈應用到并聯機器人設計中，但目前對于五桿機構作為獨立支鏈的運動性能研究系統性不足，缺乏對五桿機構最佳工作區的研究分析。

在工作空間分析上，常用的方法有幾何法和解析法[1]兩大類。Arrouk等[9]利用CAD幾何軟件求解平面并聯機器人的工作空間，避免了復雜的數值計算過程。李旭等[10]基于蒙特卡洛離散的方法求解了3T1R并聯機構的工作空間。但以上方法都是基于確定的并聯機器人構型分析工作空間的大小，缺少針對目標工作空間需求完成并聯機器人尺度綜合的正向設計方法，導致設計結果不透明，甚至出現設計結果不滿足要求的情況。

針對以上問題，本文通過建立平面五桿機構的運動學模型，基于奇異性分析和性能評價指標，完成對支鏈五桿機構的尺度綜合，實現性能最優的支鏈五桿設計。基于工作空間需求進行并聯機器人的正向設計，提出平面幾何投影法將三維工作空間轉換到平面五桿支鏈的最佳工作區，計算支鏈尺度是否滿足工作空間要求，并明確支鏈的配置范圍，設計出具有可變動平臺的并聯機器人。

1 面向性能最優的支鏈五桿設計

1.1 運動學模型

五桿機構如圖1所示，建立坐標系，5為機架桿，1和4為輸入桿，2和6為輸出桿，3為連桿，其中2＝，6＝，l為虛擬桿。點為6末端參考點，1～5分別為桿件1～5與軸正方向的逆時針夾角，其中5＝0。

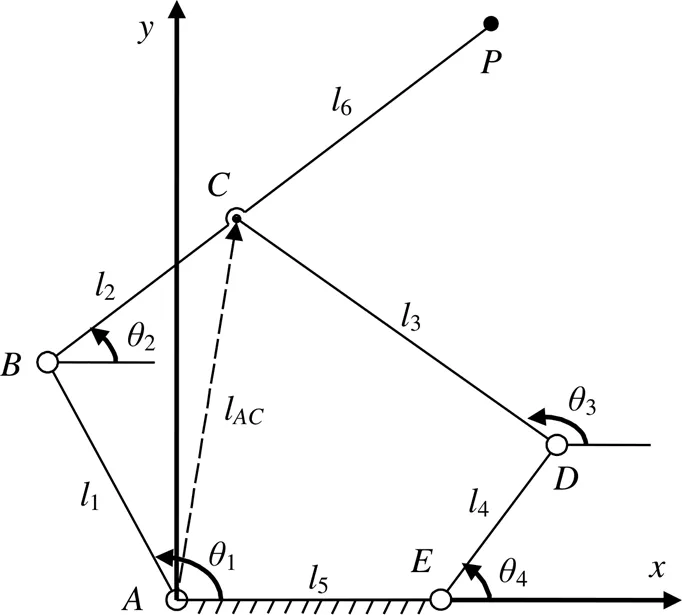
圖1 五桿機構示意圖

對于五桿機構運動學求解，由閉環矢量法建立關于點的投影方程為：

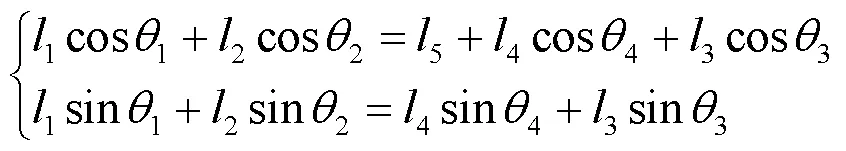
由式（1）可得：

則點位置為：

1.2 奇異性分析

機構奇異性是指當機構達到奇異位置時，導致末端無法驅動或處于運動不確定的狀態。機構的奇異性判斷一般是基于雅克比矩陣確定，對式（1）求時間導數可得：

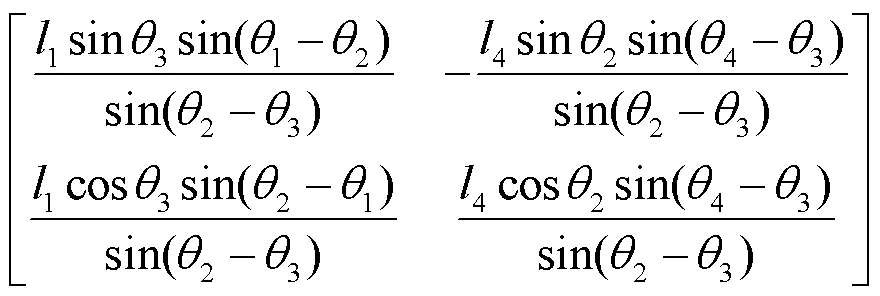
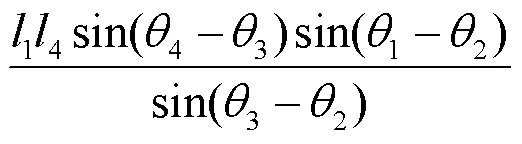
式中：為雅克比矩陣；det()為的行列式值。

式（5）表明雅克比矩陣行列式值是關于各角度參數的函數。取＝-1,0,1，則針對圖1五桿機構會出現兩種情況：

（1）當1＝2＋π或4＝3＋π時，det()＝0，此時只有當1和4的驅動速度無窮大才能在末端輸出有限的速度，機構末端達到工作空間的邊界，稱為邊界奇異；

與此同時，積極融入云南“一核一圈兩廊三帶六群”的區域發展，推進物流基地規劃和配套建設，有效發揮鐵路物流基地的集聚效應和輻射帶動作用，服務區域經濟發展和產業轉型升級。

（2）當2＝3＋π時，det()＝∞，此時機構關節運動狀態不確定，機構末端在工作空間內部，稱為內部奇異。

1.3 平面五桿機構的性能評價指標

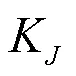
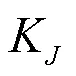
考慮到全局運動傳遞性能，文獻[12]提出：

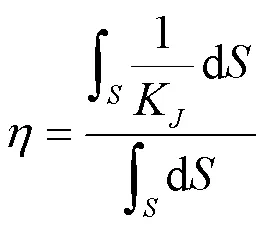
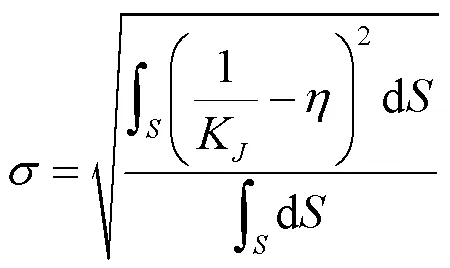
考慮機構運動過程中會出現變形，根據求出剛度矩陣＝(T)-1，得到：

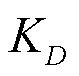
此時定義：

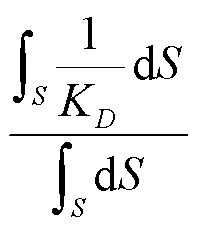
式中：為全域剛度性能平均水平指標。

在機構設計中，提高安裝空間利用率是實現經濟性的重要指標，因此針對圖1機構定義：

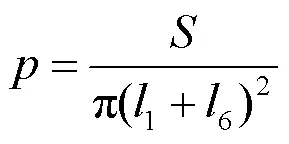
1.4 基于APSO算法的尺度綜合

在設計時，需要根據最優的綜合性能評價指標進行機構尺度優化，選擇自適應粒子群優化（Adaptive Particle Swarm Optimization，APSO）算法。APSO算法引入了自適應權重因子，能夠增強粒子群算法的全局搜索能力，避免陷入局部最優[13]。

為了實現五桿支鏈的模塊化設計，對圖1機構尺寸進行歸一化處理，使得5＝1、6＝5、1＝3、2＝4。根據設計要求[14]和性能評價指標，建立目標函數：

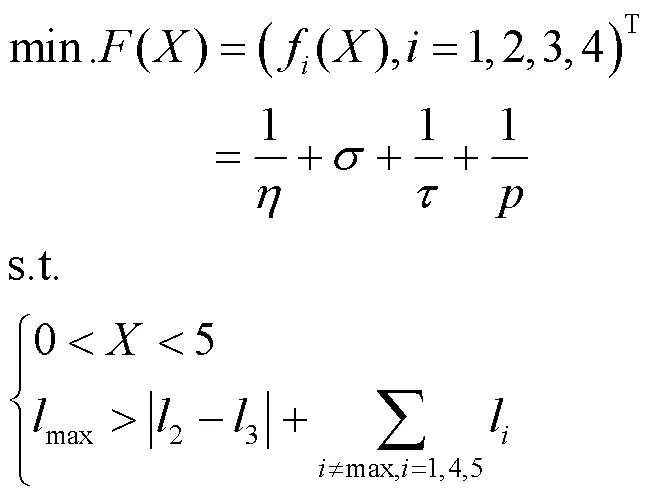
將該目標函數模型利用APSO算法實現，迭代100次，得到最優結果如圖2所示，可以看出，指標、、、都得到了優化。經過20代之后，設計變量和目標函數值趨于穩定，尋到最優結果，即＝(3.61, 1.47)。

2 面向工作空間的并聯機器人設計

基于對五桿機構的性能優化，可以配置若干對稱或非對稱的支鏈構成并聯機器人，并聯機器人的工作空間就是支鏈工作空間的交集。但由于并聯機器人正向尺度設計方法的缺少，需要建立一種基于工作空間需求進行含可變動平臺的并聯機器人設計方法，在設計并聯機器人之初就考慮所需工作空間的要求。

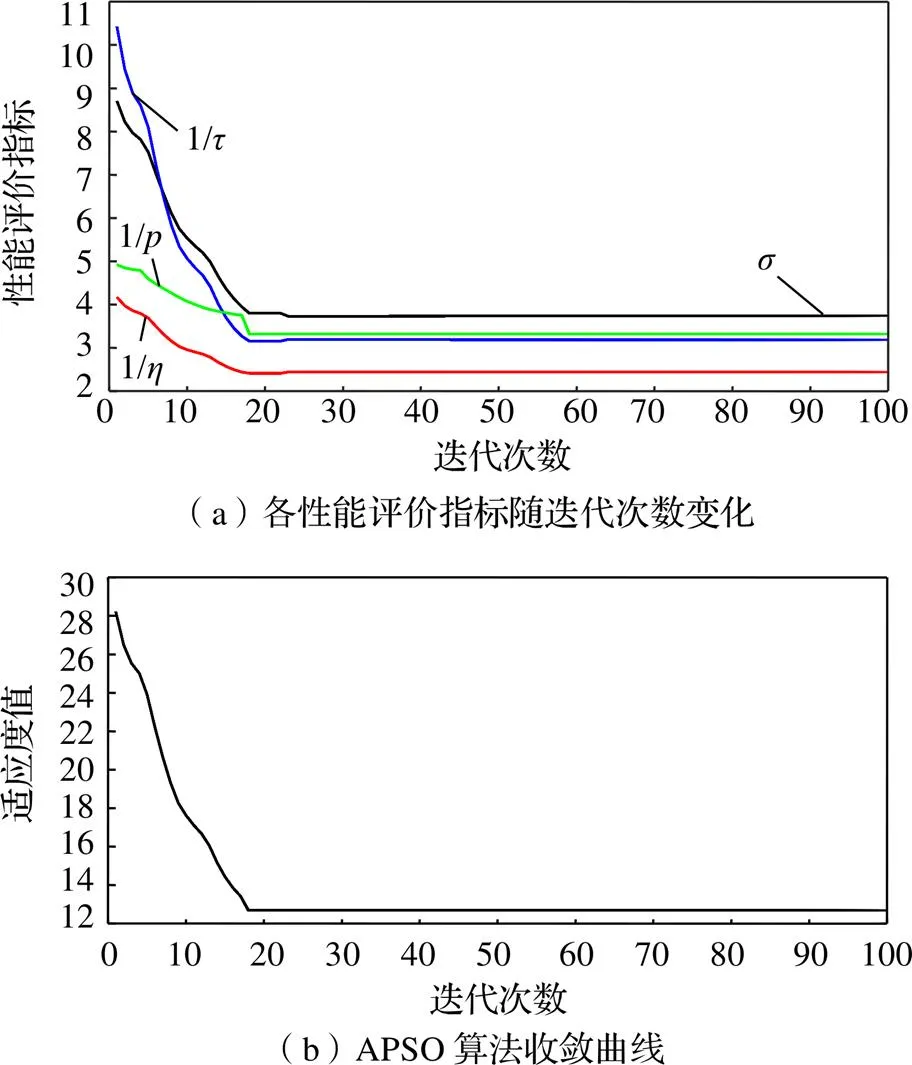
圖2 五桿尺寸比例優化結果

2.1 支鏈五桿機構的工作空間

假設所需工作空間0為200 mm×200 mm×200 mm，首先分析五桿支鏈的工作空間，根據0大小和尺度綜合的結果，選擇五桿尺寸1＝3＝361 mm、2＝4＝147 mm、5＝100 mm、6＝500 mm，建立圖3（a）所示的坐標系和五桿機構。根據并聯機器人結構要求，選擇1和4的輸入范圍為[π, 2π]，步長都為1°，采用均勻離散的方法遍歷1和4的取值范圍，保證避免并遠離奇異位置，得到五桿機構非奇異工作空間。根據運動性能評價指標，在非奇異工作空間內計算所有點的目標函數，確定支鏈五桿最佳工作區，即圖3（b）白色線條包絡區域。

2.2 基于平面投影的工作空間分析

針對由五桿支鏈組成的并聯機器人，提出一種基于平面投影的工作空間分析方法，該并聯機器人如圖4所示。

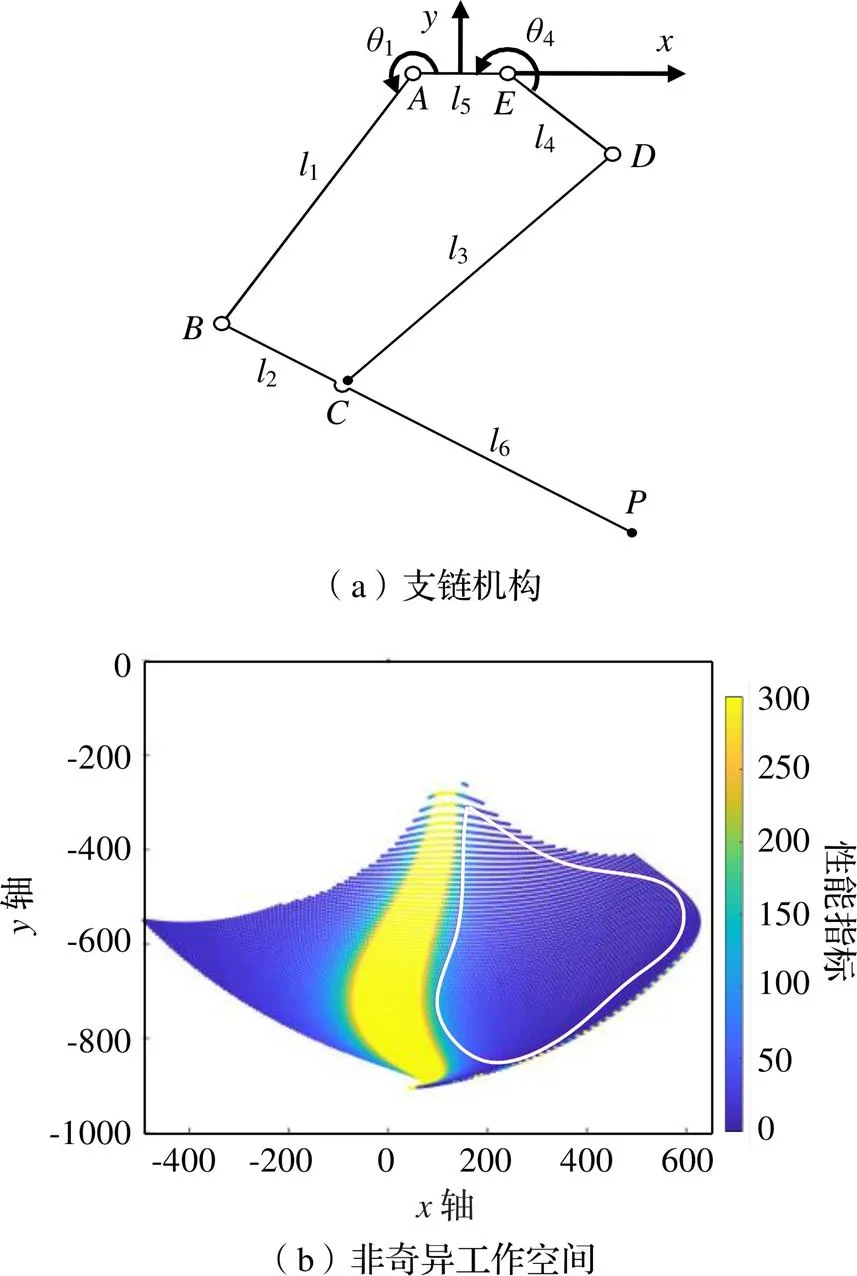
圖3 支鏈五桿機構及其工作空間

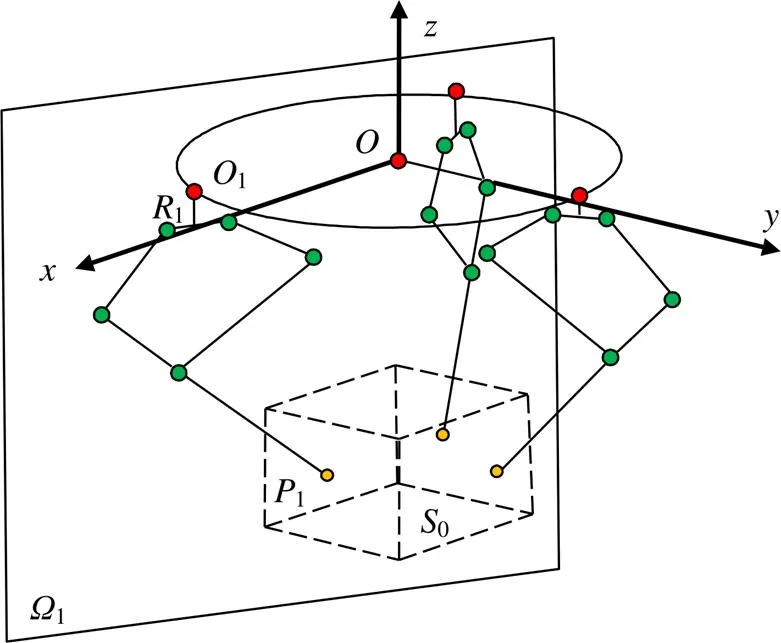
圖4 可重構并聯機器人結構模型

矩形體為所要求工作空間0，動平臺位于工作空間內，各支鏈在未抓取動平臺之前相互獨立，支鏈11為2.1節所選擇的五桿機構，與靜平臺通過轉動副1連接，1軸線和靜平臺垂直，1為支鏈11所在平面。該結構中，支鏈可以繞轉動副旋轉一周形成三維空間，并聯機器人的工作空間便是支鏈三維空間的交集。平面幾何投影方法即根據不同任務的工作空間要求，通過工作空間極限位置的平面投影，以支鏈五桿機構的最佳工作區域確定尺度是否滿足需求，并明確支鏈機架安裝范圍。

如圖5所示，將整個機構在平面上投影，為并聯機器人原點，1點為支鏈機架點，矩形為工作空間投影。顯然，1為矩形相對支鏈機架點1的最遠極限位置；1為矩形相對支鏈機架點1的最近極限位置。依據圓弧投影法，將工作空間極限點1、1往平面1上進行圓弧投影，即以1為圓心、11為半徑作圓，得到投影點2；以1為圓心、11為半徑作圓，得到投影點2。計算投影點2、2和支鏈最佳工作區的關系，就可確定支鏈尺度是否滿足要求且保證最佳運動狀態。

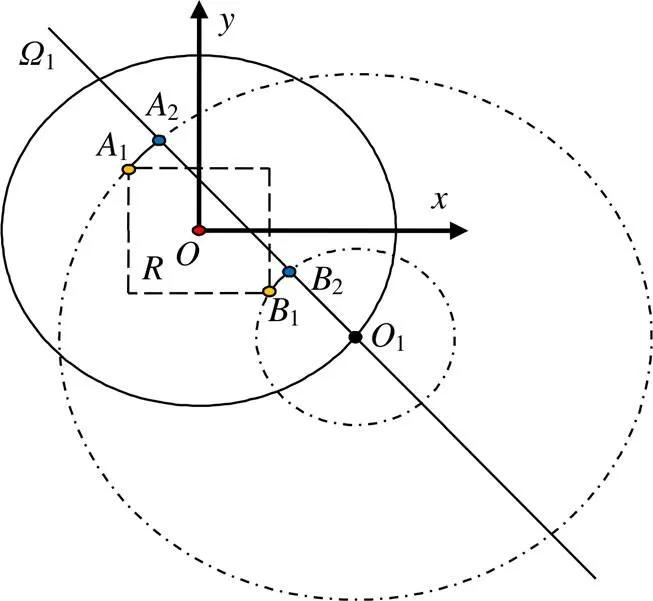
圖5 并聯機器人xOy幾何投影

在圖5中，建立基坐標系，根據給定工作空間要求，確定極限位置坐標1＝(-100, 100, -400)、1＝(100, -100, -400 )、1＝(1,1, 0)。根據幾何投影關系，在投影面上，得：

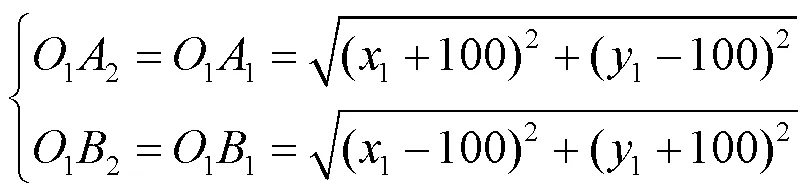
將極限投影位置轉換到五桿機構中分析，可以在最佳工作區尋到最大矩形，即圖6中的，坐標為：(160, -440)、(500, -440)、(500, -680)、(160, -680)。

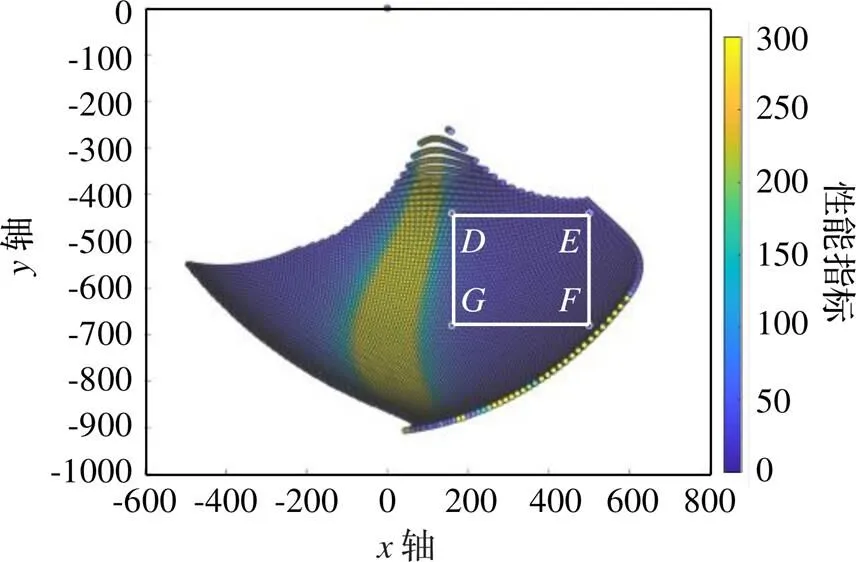
圖6 支鏈五桿機構非奇異工作空間

確定支鏈五桿機構的最大矩形后，將點、點投影到平面得到2、2，如圖7（a）所示。

支鏈機架需滿足12＜12且12＞12，可見圖7（a）支鏈機架位置并不滿足條件，因此需調整1的位置。根據幾何投影關系，機架安裝范圍具有兩個極限位置，即2和2重合，1＝304 mm，如圖7（b）；2和2重合，1＝351 mm，如圖7（c）所示。因此，可以確定支鏈機架點安裝位置在以為圓心、半徑分別為304 mm和351 mm的圓環內。

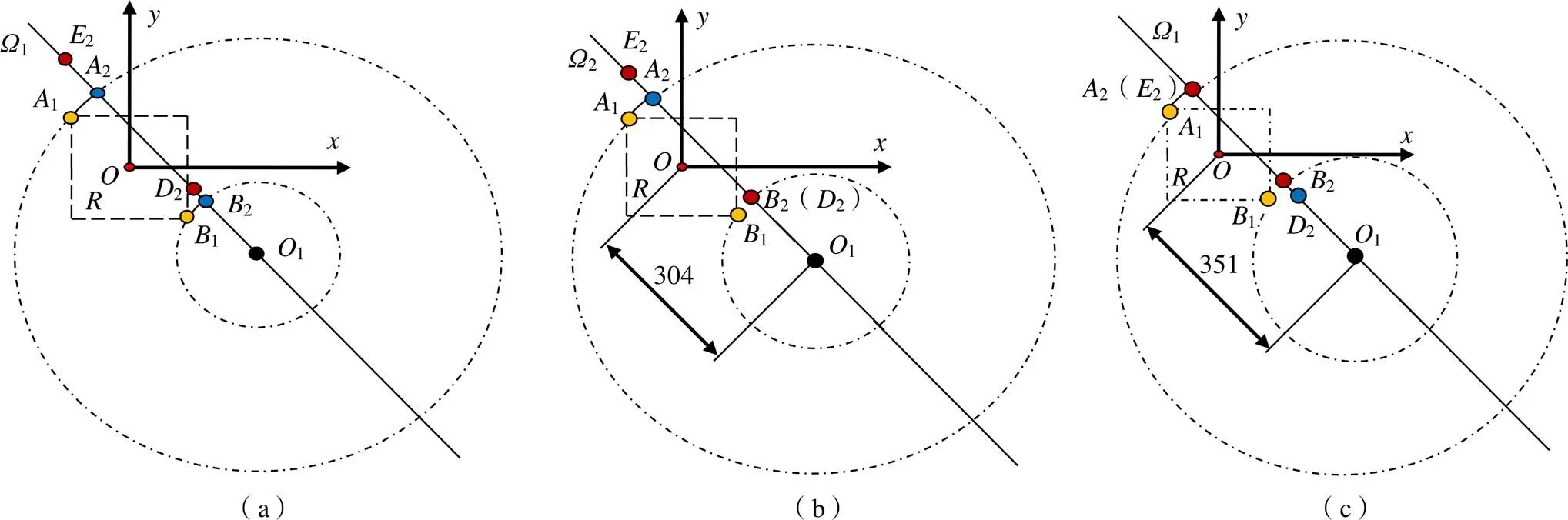
圖7 五桿支鏈機架安裝位置范圍

基于對單支鏈五桿機構工作空間的分析和平面幾何投影法，可以根據工作空間要求尋找支鏈的最佳工作區，實現多支鏈的、含可變動平臺的并聯機器人設計。假定以三支鏈并聯機器人為例，按照所選擇機構的尺寸關系，建立整個并聯機器人系統，如圖8所示。圓1和圓2形成的圓環即為支鏈可配置范圍，運動過程中，可以根據可變動平臺的位置和運動要求合理配置支鏈位置。

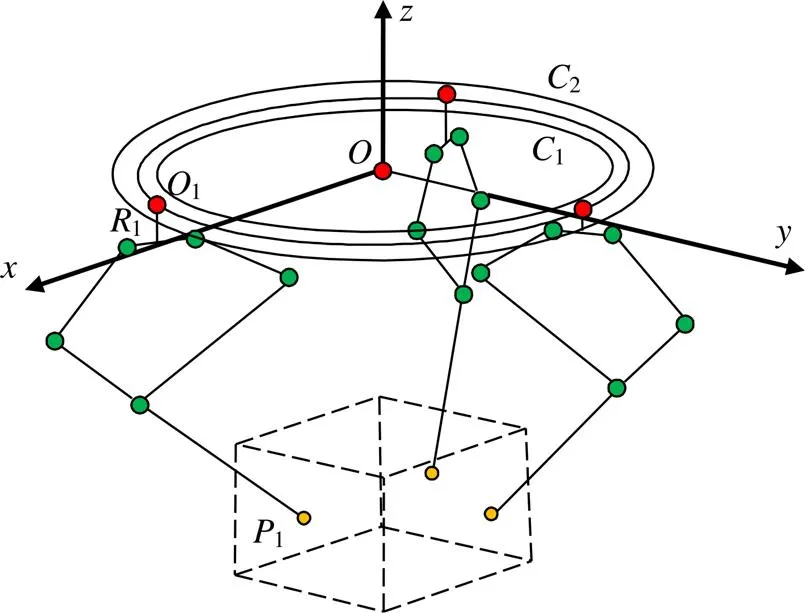
圖8 三支鏈并聯機器人結構

3 結論

本文通過解析和幾何結合的方法完成了支鏈五桿機構的運動學建模和奇異性分析，綜合出了支鏈五桿機構的性能評價指標。利用APSO算法，得到了具有最優性能的支鏈五桿尺度比例，為實現模塊化支鏈提供了依據。

利用性能最優的五桿支鏈，針對不同的工作空間要求，提出了基于極限位置平面投影的工作空間分析方法，將并聯機器人工作空間與支鏈五桿最佳工作區相聯系，簡化了三維空間分析過程，把工作空間作為設計要素納入并聯機器人設計之中，提高了并聯機器人設計的有效性和透明度。同時，可以組合不同支鏈構型應對復雜的工作空間要求，有利于實現并聯機器人的可重構設計。

[1]Merlet J P. Parallel Robots[M]. Dordrecht：Springer Science & Business Media，2014.

[2]翟慶鐘，王衛兵，馮靜安，等. 基于Stewart平臺的六軸并聯機床的研究[J]. 機械，2013，40（11）：16-19.

[3]Shen H P，Meng Q M，Li J，et al. Kinematic sensitivity，parameter identification and calibration of a non-fully symmetric parallel Delta robot[J]. Mechanism and Machine Theory，2021（161）：94-114.

[4]Liu Y J，Kong M X，Wan N. A Geometric Approach to Obtain the Closed-Form Forward Kinematics of H4 Parallel Robot[J]. Journal of Mechanisms and Robotics，2018，10（5）：1942-1951.

[5]劉辛軍，謝福貴，汪勁松. 并聯機器人機構學基礎[M]. 北京：高等教育出版社，2018.

[6]GosselinC. Adaptiverobotic mechanical systems: a design paradigm[J]. Journal of Mechanical Design，2016，128（1）：192-198.

[7]Ye W，Fang Y F，Guo S. Reconfigurable parallel mechanisms with planar five-bar metamorphic linkages[J]. Science China Technological Sciences，2014，57（1）：210-218.

[8]Markus Hoherwarter. 左臺益，譯. GeoGebra使用說明[M]. 臺灣：國立臺灣師范大學出版社，2009.

[9]Arrouk K A，Gogu G. CAD based unified graphical methodology for solving the main problemsrelated to geometric and manipulators[J]. Robotics and Computer Intergrate Manufacturing，2016（37）：302-321.

[10]李旭，羅霞，羅成，等. 基于離散蒙特卡洛的一種3T1R并聯機構工作空間分析[J]. 機械，2020，47（5）：27-32.

[11]Wang Y，Belzile B，Angeles J，et al. Kinematic analysis and optimum design of a novel 2PUR-2RPU parallel robot[J]. Mechanism and Machine Theory，2019（139）：407-423.

[12]馬麗. 基于MATLAB的小型碼垛機器人機構設計與仿真的研究[D]. 天津：天津科技大學，2016.

[13]余勝威. MATLAB優化算法案例分析與應用[M]. 北京：清華大學出版社，2014.

[14]Verein Deutuscher Ingenieure,Entwicklungsmethodik für Mechatronische System[M]. Düsseldorf：Springer，2004.

Research on Parallel Robot Design Methods Based on the Performance Optimization and Configuration of Five-Bar Chains

XU Huaian，LIN Song，JIANG Jingyu

( School of Mechanical Engineering, Tongji University, Shanghai 201804,China)

With the diversification and complexity of motion requirements, the opaqueness of traditional parallel robot design methods and the invariance of the moving platform lead to deviations in design results and a low degree of flexibility. This paper therefore proposes a parallel robot design method based on the optimisation and configuration of the performance of a five-bar chain. Firstly, the analysis of the motion and singularity of the planar five-bar mechanism was completed using a combination of analytical and geometric methods. The scale synthesis of the five rods of the branch chain was completed according to the relevant performance evaluation indicators. Then, the planar geometric projection method is proposed to project the parallel robot workspace to the optimal working area of the planar five-bar mechanism. The design and configuration of the parallel robot is completed taking into account the requirements of the workspace and the motion performance, which improves the transparency of the design.

parallel robots；pivot chain five-bar mechanism；scale synthesis；workspace projection

TH112

A

10.3969/j.issn.1006-0316.2022.05.009

1006-0316 (2022) 05-0055-06

2022-01-18

徐懷安（1997－），男，山東聊城人，碩士，主要研究方向為并聯機器人設計，E-mail：17853141235@163.com。*

林松（1957－），男，四川廣元人，工學博士（德），主要研究方向為產品研發方法及其智能設計、虛擬產品生產及其數字孿生、智能裝置及其人機協調、技術系統可靠性及其安全設計，E-mail：slin@tongji.edu.cn。