數形結合思想在小學數學計算教學中的應用

劉漢民

數形結合思想是數學教學中十分重要的思想形式，可以通過數與形之間的結合來幫助學生進行數學知識的理解，也可以幫助學生進行解題，有效促進小學生數學素養的同步提升。學生的計算能力培養十分關鍵，教師可以利用數形結合思想來進行計算教學過程中的滲透，從而實現學生計算能力的提升。那么如何才能在數學計算教學中進行數形結合思想的應用呢？筆者對此進行了探究和分析。

一、數形結合思想概述

數形結合思想是數學學習中十分重要的一種思想方式，主要是能更好地將數字和圖形進行一定的結合，從而能有效幫助學生來進行數學知識的學習和數學問題的解答。數形結合思想進行互相轉化，能將數字轉化為圖形，也可以將圖形轉化為數字。有時候數字和圖形之間是對應關系，不同的數學題中，可以進行數字的表示，也可以進行圖形的表示，可以根據具體的內容來幫助學生進行數學題意的理解，也能幫助學生找到具體的解題思路，促進學生數學計算能力的提升。

二、數形結合思想的重要性

數形結合思想對小學生的數學計算學習來講具有十分重要的作用，一方面，能培養學生的數形結合思想，讓其能在小學生的大腦中形成一定的概念，在日后的數學學習中發揮作用。數形結合是一種非常常見的思想，無論是小學數學的學習，還是后來的初中、高中數學，都會進行數形結合思想的應用，教師可以在小學初級階段的數學教學中進行數形結合思想的滲透，對學生日后數學成績和學科素養的提升起到非常重要的作用。另一方面，還能幫助學生進行計算題的解題工作，很多計算題有一點難度，對小學生而言，他們的數學學習基礎比較薄弱，解題的數量比較少。因此，在解題中會遇到一定的困難。而利用數形結合思想能更好地幫助學生進行解題，有效促進學生的數學理解，提升學生數學解題水平。

三、數形結合思想的使用原則

（一）科學性原則

教師在進行數形結合思想的運用時，應該遵循一定的使用原則，這樣才能讓課堂教學具有更好的效果。教師應該運用科學性原則來進行數形結合思想的滲透，數形結合思想雖然具有非常重要的作用，但是不是所有的計算教學都能進行應用。教師應該具體問題具體分析，不能為了應用而應用，這樣會造成形式化主義嚴重的問題出現，不但不利于學生的數學成績提升，而且會浪費數學課堂的教學時間。

（二）主體性原則

教師在小學數學計算教學中應該采用主體性的原則來進行數形結合思想的融入，教師應該明白學生才是計算學習的主體。那么就應該在教學設計中對學生的學習情況進行考慮，這樣才能進行數形結合思想的應用，讓其應用質量變得更高，促進學生學習成績的提升。教師還應該讓學生充分參與到數形結合思想的使用中，只有這樣才能讓學生對此種數學思想更了解。通過主動參與，學生在日后的自主學習中適當地進行數形結合思想的運用，從而促進學生的計算水平提升。

（三）實踐性原則

教師在進行計算教學時，應該采用實踐性的原則來進行數形結合思想的滲透。數形結合思想的學習不僅要進行理論方面知識的了解，更要通過不斷實踐練習才能為學生打牢基礎，從根本上進行概念的理解和運用。教師可以通過具體的例題分析來進行教學講解，有效促進學生的對數形結合思想的掌握，幫助學生實現自身數學計算能力的提升。教師可以利用課堂時間進行計算作業的例題分析，讓學生能不斷進行數形結合思想的應用練習，這樣才能實現對學生的學習幫助，發揮數形結合思想的有效作用。

四、數形結合思想在小學數學計算教學中的運用

（一）通過數形結合理清數量關系

教師在進行計算教學的過程中，要讓學生進行數量之間關系的厘清，這樣才能讓學生對整個計算題目更加了解，對學生的解題工作具有非常清晰的思路。因為很多數學計算題都是通過漢字的形式來進行闡述，這樣會讓學生在理解方面具有一定的困難，只有通過圖形的形式來進行展示，才能給學生更直觀的感受，促進學生進行數量之間關系的梳理。教師就可以在進行計算教學中進行數形結合思想的使用，幫助學生厘清各個數量之間的關系，提升學生的感悟能力。

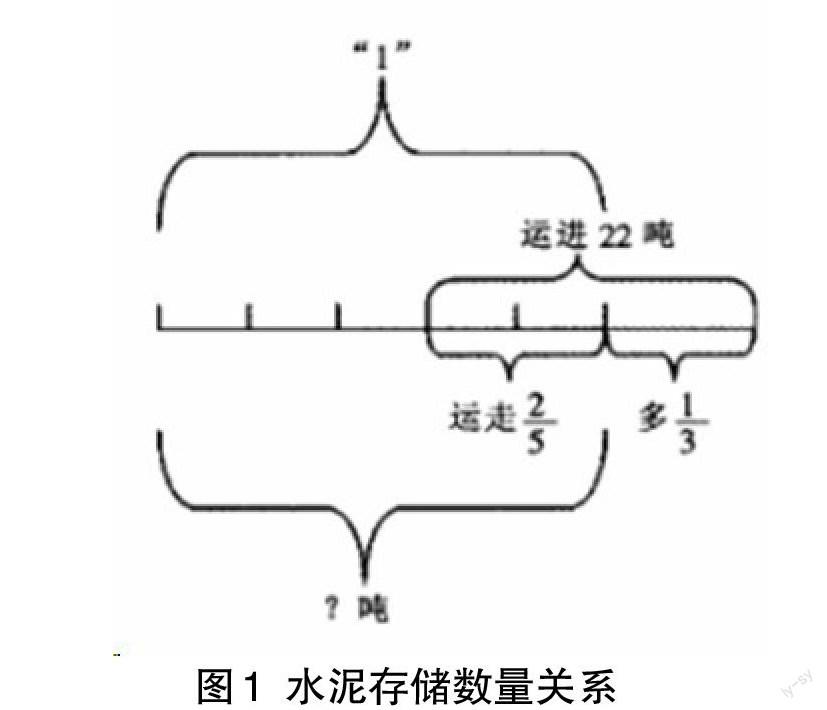
比如，在解這道題時：某倉庫中存儲了一定數量的水泥，第一天運走了整個倉庫水泥數量的[25]，第二天又運來了22噸水泥。此時，倉庫中的水泥數量比最開始多了[13]，那么請問原來倉庫里一共存儲了多少噸水泥？

一般學生在進行計算工作前，都要進行題目的閱讀和理解，但是很多學生閱讀之后都存在著一定的理解性困難。題目中的各個數量關系到底是如何呢？會在學生的大腦中產生非常多的疑問。學生之所以會產生各種疑問，是因為題目中的數量關系比較復雜，而且其中出現的分數之間可能會有一些重疊的關系，這樣會讓學生的大腦出現混亂，不利于最終的解題。那么教師就可以通過數形結合的思想來進行計算教學，讓學生能厘清題目中各個數量之間的關系，這樣才能幫助學生進行解題。題目中各個數量之間的關系如圖1所示：

教師在進行圖片的展示后，可以通過數形結合的思想來進行例題的講解，這樣能更好地幫助學生進行數形結合思想的學習，也能促進學生數學計算能力的提升。為了能讓學生成為數學計算教學中的主體，教師可以通過一定的互動形式來進行課堂教學實施。例如，教師可以問學生，從圖形中能看到什么樣的數量關系呢？可以通過學生的舉手來進行回答，也可以教師隨機進行提問。當學生課堂回答結束后，教師可以進行具體的例題講解。通過這樣的課堂互動教學，不但有助于學生的課堂思考和主動探究，還能實現學生對數形結合思想的領悟。從圖中能看到原來的水泥整體數量被看作是1，后來運走了[25]，之后又運來了22噸水泥，不僅將原來運走的[25]進行填充，還多出了原來水泥數量的[13]，那么我們就能在其中找到一定的等量關系，那么就是原來水泥量的[25]和[13]的和也就是22噸，這樣就能算出來原來的水泥量。教師已經為學生進行解題思路的查找，學生要通過這個等量關系進行計算，最后求出結果。教師通過數形結合的方式來進行例題的講解，會給學生提供更加直觀的數量關系，從而能幫助學生完成計算工作。此題雖然是計算類的應用題，但是其中的關鍵是要厘清各個數量之間的關系，利用數形結合思想可以更好地進行解題，有助于促進學生解題能力的提升。

（二）通過數形結合提高理解能力

在進行數學計算工作中，很多學生因為缺乏一定的抽象思維能力，這樣會造成對計算題無法進行深入理解，這樣不利于學生的計算題解答。那么教師就可以進行數形結合思想的運用，幫助學生理解計算題的內在原理，這樣才能讓學生真正地實現對數學計算的理解，促進學生計算水平的提升。

比如，在解[15×14=]？這道題時，因為此題為分數的計算，具有一定的難度。很多學生計算整數的乘法十分迅速，比如對5×4來講，能快速通過乘法口訣算出最后的結果是20.但是學生對分數的概念缺乏一定的理解，計算教師直接說出此題的答案，學生也不會理解，而且換一道題學生也一定會做錯。那么就要教師通過數形結合的思想來幫助學生計算，讓學生能對基本的數學邏輯進行厘清。教師可以提出問題，[15]表示什么？[14]又代表著什么？通過這樣的互動提問和回答能對單個分數的意義進行理解，這樣才能幫助學生進行接下來的乘法計算學習。學生了解到，[15]表示將一個東西5等分，然后取出其中的一份。而[14]代表將一個東西4等分，取出其中的一個。將分數的基本概念弄清楚之后，教師就可以進行繪圖工作，如圖2所示：

從圖中能看到，教師將一個正方形平均分成了5份，取其中的一份來用斜線標記，證明該區域是整個圖形中的[15]。然后教師又將[15]的區域平均分成4份，并且將其中的一份用斜線進行標記。那么[15]和[14]重疊的部分就是二者之積。通過數形結合的方法能讓學生明白分數乘法的內在含義，就是將一個整體中的一個部分再看成整體，然后再平分取出其中對應的分數，這樣就實現分數乘法的計算。教師可以讓學生通過數格子的方式來求出最后的結果為[120]，就是將整個大格子平均分成了20份，而最后的結果就是其中的一份。通過數格子解出的最后結果能看出，分數相乘就是分母相乘和分子相乘，最后得到結果。通過教師最后的總結也能告訴學生快速的分數乘法計算方法，提高學生的計算效率。

（三）通過數形結合培養空間觀念

很多學生在日常的數學學習中對平面圖形具有非常多的了解，但是對三維立體圖形的計算卻存在一定的問題。之所以會出現這樣的情況，就是因為學生不具備三維空間的觀念，對學生來講十分抽象，從而無法完成數學計算工作。那么教師就應該利用數形結合思想來進行學生空間觀念的建立，讓學生在大腦中能形成三維圖形，這樣才能幫助學生進行數學計算的思考，有助于幫助提升學生的數學計算能力。比如，在解這道題時：已知一個長方體的長度為5厘米，寬度為4厘米，高度為3厘米。那么請問長方體的占地面積是多少平方厘米？長方體的表面積是多少平方厘米？

因為很多學生無法理解長方體是三維空間圖形，在他們的心里只有長方形這樣的概念。為了能幫助學生建立三維立體圖形的概念，教師可以利用數形結合的方式來進行教學講解。教師可以通過多媒體大屏幕來進行長方體的圖形展示，為了使學生對三維空間的明晰，在圖形中運用不同的顏色而進行長、寬、高的標注，如圖3所示：

通過圖形能看到，長方體的長為紅色標注，長方體的寬為紫色標注，長方體的高為藍色標注。這樣標注能讓學生建立起初步的三維空間概念，為了能更形象地幫助學生進行三維空間的理解，可以將長、寬、高的交點看作是教室的一個角落，教室的長度、寬度和高度就分別代表了長方體的長、寬、高。通過這樣的方式能讓學生更直觀地進行三維立體圖形的觀察，也能在大腦中想象到三維圖形的樣子，有助于學生的計算工作。通過讀題，能對長方體的長度、寬度和高度進行全面了解。而題目中第一個問題是問長方體的占地面積是多少平方厘米，占地面積主要是長方體底部所占據的大小決定，那么就是長方體的底部面積，也就是用長度乘以寬度為5×4=20平方厘米。第一個計算問題已經解決，那么第二個問題是要求長方體的表面積，表面積就是所有面的面積之和。教師可以讓學生通過圖形來觀察長方體一共有多少個面，通過觀看發現一共有6個面，分別是2個長乘以寬，2個長乘以高和兩個寬乘以高，那么就能算出長方體的表面積為5×4×2+5×3×2+4×3×2=40+30+24=94平方厘米。總之，教師通過數形結合的方法能促進學生進行小學數學計算題的解答，可以幫助學生建立三維立體空間的概念，有助于學生的解題。

綜上所述，小學生的數形結合思想培養十分重要，不僅能促進學生進行數學學習能力的提升，還能在數學計算教學中發揮十分有效的效果。對小學生而言，只有學生對題目進行深入了解，才能為后續的解題工作帶來更多的思路，促進小學生計算能力的提升。

（邱瑞玲）