重構建模 發展學力

裘迪波 王孫君

[摘? 要] “運算定律”單元學習的是運算體系中具有普遍意義的規律，其中乘法分配律是學習的難點。為讓學生在大概念的統攝下，系統學習加減乘除中的三大定律，突破難點，在梳理前期學習內容、調研生情的基礎上，對本單元學習內容進行了適度整合與實踐。借助“重構模型化數學知識，培養湊整性簡算意識，感受數學思考價值”等策略，助推學生系統建模，發展學力，培養學生的高階思維能力。

[關鍵詞] 運算定律;梳理分析;整合重構;發展學力

“運算定律”（人教版四年級下冊第三單元）編排了兩節內容：先學習加法運算定律及其應用，內含連減的簡便計算;再學習乘法運算定律及其應用，練習中包括連除的應用。教材共安排了8個例題和2個專項練習。筆者用心研讀本單元教材的編排體系，結合多年的教學經驗，覺得看似清晰、系統的知識脈絡似有碎片化之感，而且每個定律平均用力，難點無法突破。為此，引發了筆者思考，筆者在梳理前期學習內容、調研生情的基礎上，對本單元學習內容進行了適度整合與實踐。

[?]一、筆者的思考

1. 能否建立“運算定律”大概念統攝教學

運算定律是數的運算體系中具有普遍意義的規律，如果將“運算律”作為大概念，那么交換律、結合律、分配律都從屬于它。在運算定律大概念統攝下，我們是否可以探索加減乘除運算中，哪些數的運算存在著交換律、結合律、分配律？能否從大概念角度進行系統教學？

2. 如何突破“乘法分配律”這一核心定律

三個乘法運算定律中，乘法分配律是學生最難理解的，也是數的運算中應用最廣泛、最能體現簡算性的運算定律，教材編排了例7作為一課時進行教學。如何才能突破這一難點，讓學生真正理解乘法分配律的內涵，并能正確地拓展應用？

3. 怎樣結合“問題解決”錘煉簡算意識

教材注重運算定律與簡便計算技巧的訓練，采用“一例一練”的方式對應編排。如何很好地將運算定律的學習和解決生活中的實際問題相結合，從而更好地培養學生的“簡算意識”？

[?]二、前置內容梳理和學情分析

（一）教材內容，前有孕伏

通過梳理前面七冊教學內容，筆者發現：一上一圖四式和二上乘法口訣對交換律有了提前滲透，三上、三下和四上通過學習多位數乘法初步體會乘法分配律、結合律以及相關的連乘、連除性質。教材整體編排對加法、乘法運算定律有了一定的孕伏。

（二）學情調測，提供依據

1. 前測分析

筆者對城區、城郊和鄉鎮三個層面的四年級6個班學生進行了學情前測，從學生認知結構、知識結構兩方面進行了調查統計。

分析統計結果，筆者發現：1、2題各層面的正確率達到了80%左右，3題各層面的正確率在50%及以下，說明學生對加法交換律和乘法交換律在認知上有了一定的感知。但大部分學生不能用文字或圖畫來表示，說明學生對交換律的內涵不是很清楚，比較模糊。4、5兩題各層面的正確率在23%和38%之間，說明大部分學生對減法和除法是否有交換律存在疑惑，學生的認知結構還缺乏完整性。

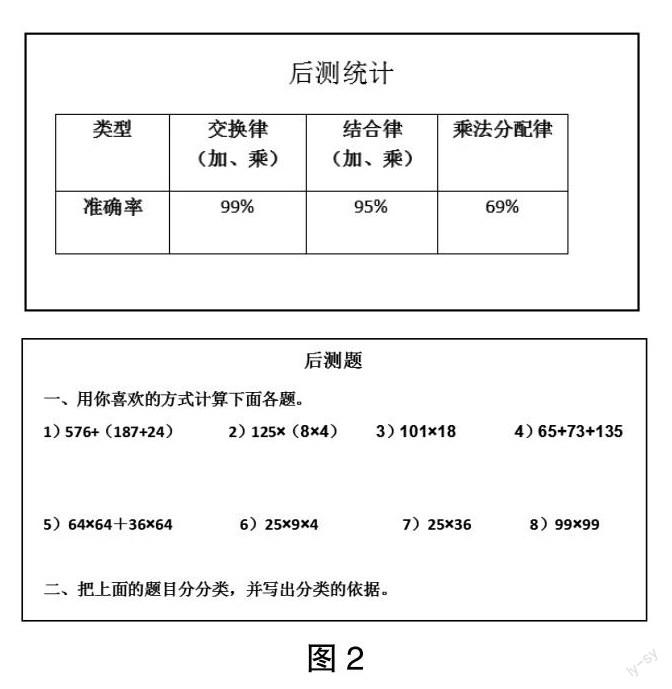
2. 后測分析

在對四年級學生進行前測的基礎上，筆者還對城區五年級學生進行了后測統計（主要從學生對知識的理解、應用意識上進行了統計）：

分析發現：學生對加法、乘法的交換律、結合律掌握得比較好，應用定律進行簡便計算正確率很高;而乘法分配律的答題情況不容樂觀，還有近30%的學生沒有掌握，不能正確應用;學生的湊整應用意識不是很強。

[?]三、單元文本的整合嘗試

在潛心研讀分析教材編排和學生前后測學情的基礎上，筆者對這單元內容進行了適當整合并確定了單元整體教學目標。

（一）研析學情，精準定位

1. 適當整合，突出大概念，系統呈現

在“運算定律”大概念統攝下，筆者將內容相似、結構相同的加法交換律和乘法交換律整合成一節交換律，把加法結合律和乘法結合律整合成一節結合律，把減法的簡便運算和連除的簡便運算整合成一節減法和除法的性質，在此之后安排一節交換律、結合律性質的綜合應用。從學生的后測情況來看，學生對乘法分配律的應用掌握不夠，所以筆者把乘法分配律分成兩節課加以突破：分別為意義的理解和應用拓展兩課時，最后為單元復習。運算定律的應用、解決問題策略多樣化等分解在定律的應用拓展以及單元復習課中。具體框架如下：

這樣整合，更有利于學生感悟知識之間的聯系與區別，完善學生的認知結構，同時突破模型結構相對復雜的乘法分配律。

2. 延長課時，突破難點，建構模型

乘法分配律具有高度的抽象性和概括性，其模型結構對學生來說很難建立。教材只安排了一個例題一課時來學習，大部分學生難以理解。筆者應拉長學習時空，拉長乘法分配律的建構過程，設計貼近生活的問題情境，充分展示思維過程來保證模型的建構，讓學生在經歷“猜想→驗證→歸納→建模”中真正理解定律的內核，培養學生高層次的數學思維能力。

3. 夯實基礎，靈活應用，錘煉意識

常態教學中，教師往往偏向簡便計算能力的訓練，忽視學生湊整意識的培養。容易造成學生看題目要求簡便計算，就進行簡算;一旦沒有這個要求，就按常規方法計算。因此，筆者應按照“前有孕伏，提前滲透;中有突破，靈活簡算;后有發展，錘煉意識”的整體性教學思路，有的放矢地錘煉學生的簡算意識。

（二）呈現價值，制定目標

為了突出單元整體性，筆者預設了“強化意義、錘煉思維、體現價值”的單元目標：

1. 強化運算定律意義的理解，建構“模型化”數學知識

讓95%以上的學生能識別和理解運算定律和性質;85%以上的學生能選擇合適的算法模型，靈活運用;70%以上的學生會運用模型，創編合適情境。

2. 提升運算定律應用的能力，培養“湊整”簡算意識

運算定律教學不能簡單等同于簡便計算教學，運用運算定律進行簡便運算的本質是湊整，培養學生湊整的簡算意識。

3. 不斷積累基本活動經驗和思考經驗，培養學生的高階思維能力

讓學生經歷觀察、發現、猜想、舉例、驗證、歸納等思考過程，感受數學思考的價值，培養學生的高階思維能力。

[?]四、單元整合教學實施策略

為實現上述目標，筆者借助重構“模型化”數學知識，培養“湊整”簡算意識，感受“數學思考”價值等策略，幫助學生重構建模、發展學力。

（一）數形交融，建構“模型化”數學知識

1. 以形促數，豐富活動經驗

教學定律時，筆者借助圖形表征，豐富學生的活動經驗，促使學生理解內化。如教學交換律時，看圖算一算：★★★? ★★★★ 一共有多少個五角星？●●●●● ●●●●一共有多少個圓？借助計算圖形個數，得出3+4=4+3，5+4=4+5。這樣讓學生體會形中有數，以形促數，使學生更加深刻地理解運算定律的意義。

2. 形中思數，強化運算本質

乘法分配律的理解和應用是本單元教學的難點。筆者借助圖形表征、符號表征等不同方式來促進學生理解定律的本質。如讓學生計算長方形的面積（如圖4），有的學生用101×50，有的用100×50+1×50。

101×50 100×50+1×50

=（100+1）×50 =5000+50

=100×50+1×50 =5050

=5000+50

=5050

通過兩種方法計算面積，讓學生“形中思數”，借助圖形的直觀性將抽象的運算定律形象化、簡單化，讓學生運用多種感官充分感知，搭建數與形之間的橋梁，學生對“以形思數”的感悟會有更高層次的理解，從而強化運算定律的本質。

3. 數形互補，構建數學模型

筆者還嘗試借助圖形來進行乘法分配律的教學（如圖5：媽媽各買了3盒兩種規格的口罩，媽媽總共買了多少個口罩？）讓學生結合點子圖表述所寫算式（5+7）×3=5×3+7×3的含義。

這樣借助圖形從分到合或從合到分進行動態展示，巧用圖形表征給學生一個“理解的支點”，一方面借助圖形可以探索出運算定律，體現“數中有形”;另一方面利用圖形呈現的多樣性，可以發現數的運算規律，體現“形中有數”。這樣一種教學方式讓學生真正感受到數形結合的魅力。數形互補，促使學生主動建構乘法分配律。

（二）一題巧用，培養“湊整性”簡算意識

1. 一題多解，錘煉簡算技能

如計算50+25×88，引導學生用不同的方法解決：50+25×（80+8），50+25×4×22，50+25×8×11，25×2+25×88=25×（2+88），既應用了乘法分配律，又涉及了乘法結合律。通過一題多解，靈活簡算，錘煉學生的簡算技能。

2. 一題多變，激活簡算意識

如在復習運算定律時設計下題：

25×43_______，在橫線上填寫數與運算符號，使式子能簡便計算。

這題會呈現多種結果，如25×43×4、25×43+25×57等，既有應用乘法交換律、乘法結合律的簡算，又有應用乘法分配律的簡算。這樣的一題多變，可激活學生的簡算意識和簡算思維。

3. 一題多編，靈活簡算應用

如教學單元綜合應用時，讓學生選取125、32、68、8、101中的任意幾個數，編寫一個能簡便計算的式子，并說明用什么定律或性質。學生可能會編出：125×32=125×8×4，68×101=68×1+68×100，等等。在經歷自主編題、思考的過程中，進一步錘煉了學生的簡算意識和運算技能。

（三）積累經驗，感受“數學思考”的價值

運算定律的學習過程是后續代數知識學習的基礎，也是后續學生靈活處理計算問題積累相應活動經驗的過程。因此，教學時要盡可能拉長、凸顯這個過程，讓學生在不斷經歷數學活動的過程中積累經驗，感受數學思考的價值。

1. 從“探究嘗試”走向“猜想驗證”

如學習交換律時，當學生通過觀察引發猜想、自主驗證，發現并歸納出加法交換律后，教師追問“加法中有交換律，其他運算中是否也存在著這樣的定律呢？”由此引導學生從加法遷移到四則運算，讓學生再次提出猜想：有的說乘法中可能也有交換律，有的認為減法和除法中可能也有交換律。然后根據學習單讓學生自主舉例驗證，交流反饋，得出結論。兩次猜想、驗證，進一步錘煉了學生的思考能力和學習能力，促使學生的思維從低階步入高階。

2. 從“歸納建模”走向“數學應用”

如探究乘法分配律時，筆者設計了以下四個練習：

（1）在○里填上<、>或=。

（4+2）×25○4×25+2×25，8×（125+25）○8×125+8×25。

（2）請再舉幾個這樣相等的例子。

（3）請用字母表示上述相等的式子。

（a+b）×c=___×___+___×___，a×（b+c）=____×____+____×____。

（4）用乘法分配律計算：125×（8+4），64×64+36×64。

筆者先讓學生判斷左右兩邊的式子是否相等，再根據等式兩邊的變化過程，歸納建模，用字母表示出定律，最后應用定律進行簡算。一步步引導學生從數到符號，從直觀到抽象，從歸納到應用，推動著學生思維向縱深發展。

這樣的單元整合學習，學生經歷了一次次深入的探究活動，建構了一個個運算定律模型，深度學習在探究驗證、重構建模中真實地發生著。