例說中考中的翻折問題


江建華中學數學高級教師, 中國數學奧林匹克貳級教練員,湖北省中學數學省級骨干教師,黃石市中學數學學科帶頭人,發表多篇論文,曾主編《初三幾何完全解讀》等著作。
翻折問題既是中考命題的熱點問題,也是學生解題的難點問題,翻折問題實質上是圖形的軸對稱變換,解題時可以利用軸對稱圖形的性質,結合全等的判定與性質、相似的判定與性質、圓的性質、勾股定理和三角函數等知識進行求解.
1 三角形中的翻折
例1 圖1
如圖1,在Rt△ABC紙片中,∠ACB=90°,AC=4,BC=3,點D,E分別在AB,AC上,連接DE,將△ADE沿DE翻折,使點A的對應點F落在BC的延長線上,若FD平分∠EFB,則AD的長為.
(A)259.(B)258.
(C)157.(D)207.
圖2
解 如圖2,過點D作DH⊥BC于點H,
因為∠ACB=90°,
所以AB=BC2+AC2
=32+42
=5,
因為將△ADE沿DE翻折得△DEF,
所以AD=DF,∠A=∠DFE,
又因為FD平分∠EFB,
所以∠DFE=∠DFH,
所以∠DFH=∠A,
所以sin∠DFH=sin∠A=BCAB=35,
又因為sin∠DFH=DHDF,
所以DHDF=35,
設DH=3x,則有
DF=AD=5x,
所以BD=5-5x,
因為DH∥AC,
所以△BDH∽△BAC,
所以BDAB=DHAC,
所以5-5x5=3x4,
所以x=47,
所以AD=5x=207.
故選(D).
2 矩形中的翻折
例2 圖3
如圖3所示,在矩形紙片ABCD中,AB=3,BC=6,點E,F分別是矩形的邊AD,BC上的動點,將該紙片沿直線EF折疊使點B落在矩形邊AD上,對應點記為點G,點A落在M處,連接EF,BG,BE,EF與BG交于點N.則下列結論成立的是().
①BN=AB;
②當點G與點D重合時,EF=352;
③△GNF的面積S的取值范圍是94≤S≤72;
④當CF=52時,S△MEG=3134.
(A)①②. (B)③④.
(C)②③.(D)②④.
圖4
解 ①如圖4,因為
∠A=90°,
AB=3,
AD=BC=6,
所以BD=AB2+AD2
=32+62
=35,
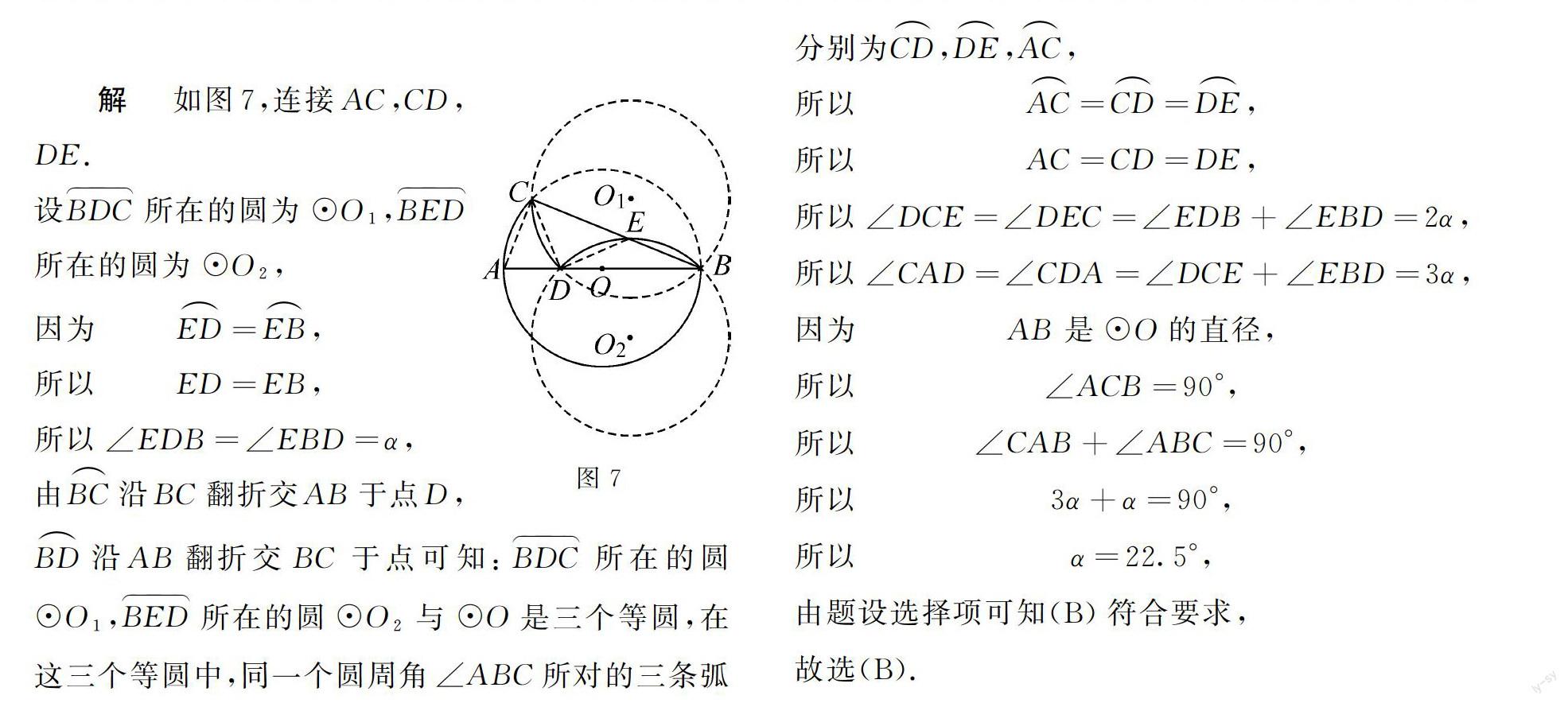
所以3 由BN=12BG,可知BN的值是變化的,而AB=3是定值, 所以BN與AB不一定相等,故①錯誤; ②如圖4,當D,G重合時,因為四邊形ABCD是矩形,所以AD∥BC, 所以∠DEF=∠EFB, 由翻折的性質可知 FB=FG,∠EFB=∠EFG, 所以∠GEF=∠EFG, 所以GE=GF=BF, 因為GE∥BF, 所以四邊形BEGF是平行四邊形, 因為FB=FG, 所以四邊形BEGF是菱形, 所以BE=EG, 設BE=x,則有DE=x, AE=AD-DE=6-x, 因為AB2+AE2=BE2, 所以32+(6-x)2=x2, 所以x=154, 即DE=154, 因為S菱形BEDF=DE·AB=12·BD·EF, 所以EF=2DE×ABBD=2×3×15435=352, 故②正確;圖5 ③當點A,E重合時,如圖5,△GNF的面積最小, 最小值=14S正方形ABFG =14×32=94, 當D,G重合時,如圖4,△GNF的面積最大, 最大值=14S菱形BFGE=14×154×3=4516, 所以94≤S△GNF≤4516, 故③錯誤; ④如圖3中,當CF=52時, BF=BE=BC-CF=6-52=72, GM=AB=3, 所以AE=EM=BE2-AB2 =722-32=132, 所以S△MEG=12·ME·GM =12×132×3 =3134. 故④正確. 故選(D). 3 圓弧的翻折 例3 圖6 如圖6,AB是⊙O的直徑,BC是⊙O的弦,先將BC沿BC翻折交AB于點D,再將BD沿AB翻折交BC于點E,若BE=DE,設∠ABC=α,則α所在的范圍是() (A)21.9°<α<22.3°. (B)22.3°<α<22.7°. (C)22.7°<α<23.1°. (D)23.1°<α<23.5°. 解 如圖7,連接AC,CD,DE. 設BDC所在的圓為⊙O1,BED所在的圓為⊙O2, 因為ED=EB, 所以ED=EB, 所以∠EDB=∠EBD=α, 由BC沿BC翻折交AB于點D,BD沿AB翻折交BC于點可知:BDC所在的圓⊙O1,BED所在的圓⊙O2與⊙O是三個等圓,在這三個等圓中,同一個圓周角∠ABC所對的三條弧分別為CD,DE,AC, 所以AC=CD=DE, 所以AC=CD=DE, 所以∠DCE=∠DEC=∠EDB+∠EBD=2α, 所以∠CAD=∠CDA=∠DCE+∠EBD=3α, 因為AB是⊙O的直徑, 所以∠ACB=90°, 所以∠CAB+∠ABC=90°, 所以3α+α=90°, 所以α=22.5°, 由題設選擇項可知(B)符合要求, 故選(B).

