電力系統暫態功角失穩與暫態電壓失穩的主導性識別
李凱恩,石定中,張 磊,楊明貴,劉 勇
(云南電網有限責任公司臨滄供電局,云南臨滄 677000)
0 引言
電力系統故障后暫態過程體現為暫態功角失穩和電壓失穩,一旦出現電力系統失穩,比如功角失穩會從一定程度上導致電壓崩潰,而電壓崩潰會引發功角失穩。通常暫態功角失穩和電壓失穩往往相互交織,僅通過電壓和功角無法準確分辨系統故障之后的失穩模式。目前研究學者提出多種功角電壓失穩的實用判據和理論判斷。為此本研究從大型變電站變電斷面有功功率的特點著手,詳細闡述了暫態功角失穩和電壓失穩模式提出主導系統變量,并進一步提出識別系統主導失穩模式的方法,通過仿真分析證明該方法的有效性。
1 電力系統失穩后主導系統變量
1.1 變電斷面有功功率
對于一些大型電力系統來說可根據系統任意變電斷面潮流方向,將該系統作為簡單受送端模型。在其模型中送端系統為A 區域具有發電性質,受端系統為B 區域,具有負荷性質,結合送受端系統的特點能夠將其等值為單機單負荷。

上述公式忽略電力暫態中線路參數的變化,可將電力暫態中變電斷面電磁功率利用全微分公式進行表示。

根據上述公式,兩端母線電壓變化量以及電壓相角差變化量即變電斷面功率的變化。
1.2 選取主導系統變量值
電力系統可根據失穩后主導系統變量來區分功角或電壓穩定問題,選擇合適主導系統變量是十分重要的。本質上,電力系統是能量傳輸系統,是由變電站、電源、負荷和電網構成的,一般主要分析電源側功角問題以及負荷測電壓問題。根據方程可知,功角從本質上是由于不平衡功率導致的,與線路遙控功率有一定聯系,而電壓穩定主要與系統向負荷供電能力有關,本質上屬于線路有功功率問題。可將上述公式進行轉換為:

在該公式中,電力系統暫態中變電斷面有功功率變化量分為:第一與母線電壓相較有關,能夠作為母線電壓相角差變化量;第二與母線電壓變化程度相關,可作為母線電壓負值變化量。在擾動之后,電力系統暫態中兩個變量能夠從一定程度上決定系統之間變電斷面功率變化,進而影響整個電力系統穩定性,因此可將上述兩個變量作為主導系統變量,進一步分析電力系統電壓和功角穩定相關問題,并闡述該變量電力系統失穩模式之間的關系。
2 分析電力系統的失穩模式
電壓和功角失穩可以用ΔPδ、ΔPv表示:當電力系統運行點超過該曲線不平衡點時電力系統會進入功角失穩模式,而當電力系統運行點越過曲線中PMax點,這種情況下電力系統會進入電壓失穩模式。
2.1 電壓失穩模式
一般來說,在電力系統失穩過程中電壓和功角失穩會同時發生,這種情況下電力系統運行點會位于電壓和功腳失穩區間范圍內。根據曲線可以發現,變電站的配電電磁功率會隨著功角差增加而逐漸降低,負荷功率會隨電壓降低而逐漸降低,對于受送端的電力系統來說,送端系統A 所發出的電磁功率可用功率Pe表示,受端系統B 實際電磁功率可用P1表示,如果忽略電磁損耗,此時電磁功率與受端系統功率是相等的。當主導失穩為電壓失穩狀態時此時根據電壓穩定性概念,系統對負荷供電能力無法滿足實際負荷需求,也就是負荷實際電磁功率低于負荷所需要的功率,則有:

2.2 功角失穩模式
當電力系統處于失穩狀態時并且電壓和功角同時是處于失穩模式,根據曲線可以發現,發電機輸出電磁功率隨功角差的變化以及負荷實際功率隨電壓的變化規律仍然成立。當主導失穩狀態表現為功角失穩模式時,根據功角穩定性可以發現,在發電機的轉子中存在不平衡轉距,進一步可以發現當受送端電力系統處于失穩狀態,此時受送端A 等值變電站變電功率應當高于系統A 所配電輸出電磁功率,如果忽略電磁損耗,此時電磁功率與受端系統獲得的功率是相等的。預測未來電力系統會出現功角失穩,且目前未出現失穩,則上述公式不成立,但采用預測的方式則上述公式是成立的,因此僅需確定電力系統出現功角失穩作為主導失穩則上述公式成立。
一般電力系統失穩為單一失穩,也就是系統出現純電壓失穩或純功角失穩,這種情況下典型電壓失穩可以利用無窮大母線接入單負荷進行表示。當處于純電壓失穩時,電壓相位角變化可以忽略,進而Δδ 接近0,則:

同時,對于功角失穩來說,可以利用單機無窮大母線系統來表示,并且在純功角失穩時可忽略母線電壓負值變化量,進而ΔV=0,則:
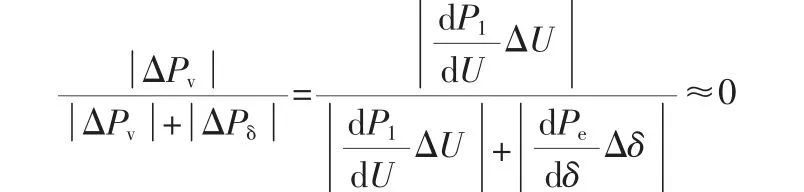
根據上述公式可以發現,本質上純電壓失穩模式與電壓失穩為主導失穩具有相同特點。同理,純功角失穩與功角失穩為主導的失穩模式同樣具備相同特征,因此可以將純電壓失穩和純功角失穩可作為主導失穩的兩種極端進行分析。
3 功率全微分的失穩模式識別
結合上述分析,同感變電斷面有功功率全微分方程可獲得變電斷面有功功率變化量包含兩個函數值。根據處于不同失穩狀態下具備不同特點來看,當主導失穩模式為電壓失穩模式,這種情況母線電壓幅值會影響變電斷面功率改變量而出現純電壓失穩,此時全部由母線電壓負值分量來決定;對于功角失穩這種情況,變電斷面功率改變量主要是與部分母線電壓相角差分量有關,在處于純功角失穩下則全部由母線電壓相角差分量決定,進而可獲得主導失穩模式的識別指標S,其中。
以S 作為主導失穩模式的識別指標,可以利用變電斷面功率改變量以及分量曲線幾何距離進行表示,當主導模式為功能失穩,這種情況下量曲線距離較小具有較高的重合度,在極端條件下兩個曲線會重合,這種情況下也使ΔPδ是導致變電斷面功率改變量發生變化的主要因素。因此,對于基于主導失穩模式識別指標,在進行電力系統失穩模式主導識別過程中:當負荷S 介于0~1/2 時,此時主導失穩模式為功角失穩;當S 介于1/2~1時,此時主導失穩模式為電壓失穩;當S 等于1/2 時,兩分量相等,處于臨界值無法準確識別系統的主導失穩模式,需要進一步分析。在這一過程中主導性識別指標并不是系統穩定判斷的能力,需要結合失穩數據進行判斷,當系統失去穩定時需要利用主導性識別指標進而確定主導性失穩模式,能夠為后續采取緊急措施提供依據。
4 仿真分析
(1)本研究提出利用功率全微分失穩模式主導性識別法。針對該方法實現仿真分析,利用電力系統全過程動態仿真程序中擾動響應數據,進一步模擬電力系統實時測量數據,以證明該方法的有效性,并使用3 機10 節電等值系統。該系統的負荷模型為:100%恒阻抗負荷為B7,電動機負荷為B10,在0 s B6位置出現三相短路故障,在經過0.005 6 s 之后該故障切除。根據穩定曲線可以發現,目前該系統出現電壓失穩模式,根據電壓曲線進一步發現受端區域的電壓持續降低,計算主導失穩模式識別指標,可以發現主導失穩模式識別指標均大于0.5,證明此時電壓失穩為系統的主導失穩模式,需要采取切負荷緊急控制措施,在2.58 s 時切除B10 位置的負荷,且根據電壓和功角曲線可以發現,通過切負荷措施之后能使電力系統恢復正常運行。
(2)使用IEEE9 節電系統。在該系統中各負荷均為恒阻抗,在0 s 時線路bus5~7 出現電路故障。結合曲線可以發現,此時電壓和功角失穩同時存在,如果單從電壓、功角的形式上很難準確判斷目前系統主導失穩模式,因此無法采取有效緊急控制措施,進一步計算主導失穩模式識別指標S,結果發現S 均低于0.5,證明此時系統功角失穩是其主導失穩模式,需采取切機措施。0.3 s 時在B2 位置進行發電機切機,為經采取措施之后根據電壓和工作曲線可以發現,采取前期措施是有效的,能夠使電力系統恢復穩定運行。
5 結束語
對于電力系統變電站出現故障采取緊急措施時,準確區分暫態功角和電壓失穩是其前提。在基于變電系統斷面有關功率特點分析的前提下,能夠利用功率全微分方程提出主導系統變量,該變量能夠用于反映系統失穩模式。結合現有失穩判據,利用提出的系統失穩識別模式能為后續暫態穩定措施提供重要依據。

