基于深度學習和PnP 模型的激光跟蹤儀自動姿態測量

周道德，高豆豆，董登峰*，周維虎，崔成君

（1.中國科學院 微電子研究所，北京 100029；2.中國科學院大學，北京 100049）

1 引言

隨著制造業的快速發展，在航空航天、汽車裝配等領域，大尺寸高精度姿態測量技術越來越重要。六自由度激光跟蹤儀是一種能夠快速高精度完成姿態測量的精密儀器，具有測量精度高、測量速度快和測量范圍廣等優勢，在高端制造業和科學工程領域有著廣泛的應用需求［1］。目前，商用六自由度激光跟蹤儀均為API、Leica、FARO 等外國公司的產品。我國對于激光跟蹤六自由度測量的研究較少，華中科技大學、上海交通大學、天津大學等基于盾構機的工作場景，對六自由度測量進行了研究［2］，利用全站儀以及角錐棱鏡完成三維位置信息的采集，利用CCD相機以及傾角儀完成姿態測量，但受到傾角傳感器的影響，具有測量范圍有限、響應速度較低等問題。為了使自主研發的三自由度激光跟蹤儀具備六自由度測量能力，本文提出一種面向激光跟蹤儀的視覺姿態自動測量方法，其基本思路是在激光跟蹤儀上增裝單目相機，在跟蹤儀測量靶標上增加三維視覺標識，從而在激光跟蹤儀測得被測工件三維坐標的基礎上，實現對被測件空間姿態的測量。

目前，主流方法使用單目相機來完成視覺位姿（即位置和姿態）的測量［3］。單目視覺位姿測量主要包括以下兩種方法：（1）利用深度網絡直接回歸出位姿參數，6D-VNet［4］、SSD6D［5］等直接回歸法缺乏顯式的幾何約束關系，精度較低［6］，這種方法實際是解決圖像檢索任務，因此回歸出的位姿參數精度仍然受限于圖像檢索精度［7］；（2）基于3D-2D 特征點的PnP（Perspective-n-Point）位姿估計方法，該方法將位姿求解作為一個幾何問題進行優化，精度較高，是目前的研究熱點［8］。當3D-2D 點之間的對應關系未知時，PnP 退化為盲PnP 問題［9］（Blind-PnP，BPnP），傳統的單目視覺算法通過人工匹配特征點再利用PnP 方法完成位姿求解。得益于深度學習的快速發展，一些工作利用深度網絡強大的學習能力獲得2D-3D 特征點的對應關系后再利用PnP 模型求解位姿［9-11］。但PnP 位姿求解作為一個幾何優化過程，其不可微性導致無法集成在深度網絡中，即其高精度的位姿求解能力無法指導網絡訓練。為了在一個端到端網絡中同時實現深度網絡的學習和幾何算法的優化，DSAC［12］方法利用中心差分來計算PnP 求解過程的偏導數，對于n維輸入，需要求解2n次完整的PnP 過程，才能獲得完整的雅克比矩陣；DBPnP［13］網絡利用聲明層理論實現PnP 位姿求解過程對網絡訓練的指導，但需要耗費較多的資源計算多個二階偏導數矩陣的逆，且存在運算不穩定的問題。

綜合考慮激光跟蹤儀對姿態測量精度、速度以及自動化測量的要求，本文提出一種深度學習與經典PnP 模型相結合的姿態測量方法，對單目相機采集到的跟蹤儀靶標圖像進行預處理得到2D 特征點坐標，使用靶標上預設特征點的3D 坐標以及圖像中2D 特征點坐標直接實現姿態的自動測量，對國內現階段激光跟蹤儀的姿態測量需求具有重要的參考價值。

2 基于深度學習的姿態測量方法

本文結合深度學習以及PnP 模型對激光跟蹤儀靶標進行姿態測量。整個測量系統主要由激光跟蹤儀、相機和靶標組成，目標是求解靶標坐標系Ot相對于相機坐標系Oc之間的旋轉矩陣（也可以表示為航天航海領域常用的RPY 角形式，定義x軸對應俯仰角、y軸對應偏航角、z軸對應橫滾角），其示意圖如圖1 所示。在對相機拍攝的圖像進行預處理得到2D 特征點坐標后，可以直接使用姿態測量網絡結構進行姿態求解，姿態測量網絡的解算流程如圖2 所示。

圖1 激光跟蹤姿態測量系統示意圖Fig.1 Schematic diagram of laser tracking attitude measurement system

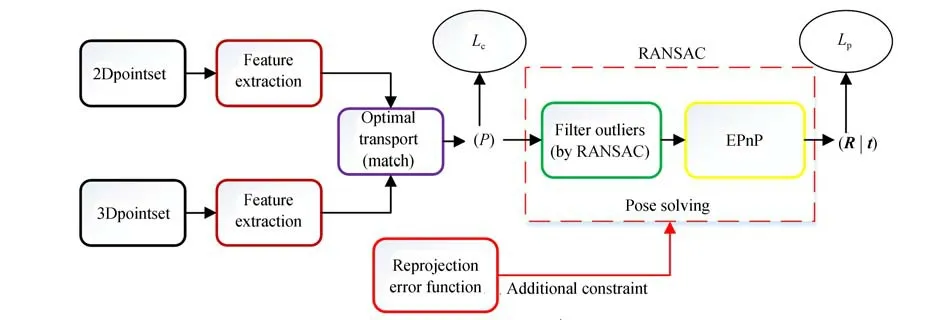
圖2 姿態解算流程Fig.2 Flow chart of attitude solution

該姿態測量網絡的解算過程主要分為特征提取、特征點匹配和姿態求解3 個步驟。首先，通過特征提取以及特征點匹配兩部分結合確定PnP 模型求解姿態時所需的特征點匹配關系；在姿態求解時，利用已確定的特征點匹配關系以及已知的坐標信息結合PnP 模型完成高精度的姿態解算。假設已經對相機圖像預處理得到了2D特征點坐標，且3D 特征點坐標已知。

2.1 特征提取

在激光跟蹤儀的工作場景下，特征點之間的對應關系往往是未知的，是一種典型的BPnP 問題，無法直接使用PnP 模型進行姿態求解，直接對原始特征點進行匹配相當困難。由于深度學習在提取數據隱含的特征時體現了無與倫比的強大潛力，為了實現特征點的自動匹配，本文使用深度學習的方式，首先提取輸入特征點有區分性的特征以便完成后續的特征點匹配。網絡的原始輸入為2D 和3D 特征點的坐標，輸入（2D 特征點和3D 特征點）首先通過一個預卷積層調整為相同的維度后，使用由8 個殘差塊（ResBlock）跨層連接組成的特征提取網絡對2D 特征點和3D 特征點進行特征提取，特征提取網絡如圖3所示。

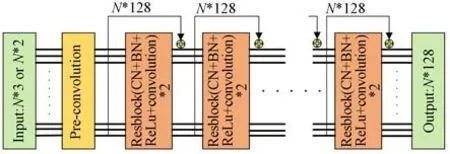
圖3 特征提取網絡Fig.3 Feature extraction network

激光跟蹤儀工作過程中，隨著靶標位姿的改變，圖像中的2D 特征點分布會發生劇烈變化。為了提取到具有強不變性的特征，本文在提取單個輸入點的特征時利用上下文歸一化［14］（Context Normalization，CN）操作將全局信息加入到特征提取網絡中，通過特征向量的分布對特征進行歸一化，從而指導每個點的特征提取。具體來說，每個殘差塊中分別包含兩個卷積層以及兩次上下文歸一化和兩次批次歸一化操作（Batch Normalization，BN），使用ReLU 函數作為殘差塊中每個神經元的激活函數。將第i個樣本在第l層的輸出向量記為，第l層的均值向量和標準差分別為：

本文對特征提取網絡進行了改進：（1）采用預激活策略，在每個殘差塊內部先進行CN、BN操作和ReLU 函數激活，卷積層放在激活函數之后，消除了殘差塊非負輸出對特征提取的影響，提升了特征提取網絡的性能；（2）針對激光跟蹤儀姿態測量時靶標坐標系固定的特點，去掉了3D 點特征提取前常用的規范化操作，和改進前的網絡相比，網絡的參數量下降了約30%，在不影響效果的前提下使模型更適合部署到激光跟蹤儀的生產環境中。最后，得到第i個特征點的128 維特征向量：記為zi∈R128。

2.2 特征點匹配

基于PnP 模型的高精度位姿求解需要確定特征點之間的匹配關系，本文利用具有強不變性的高維特征，將特征點匹配作為一個優化問題，通過優化求解特征向量之間的最優傳輸問題得到特征向量之間的匹配概率，從而完成特征點匹配。

定義3D，2D 特征點的特征向量之間的距離為：

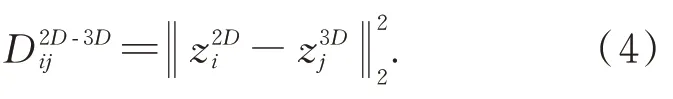
基于定義的向量間距離，對所有2D-3D 特征點對應的特征向量形成距離矩陣D，熵正則項平滑后的特征點匹配的最優傳輸問題可以寫為：

其中：＜，＞表示兩個矩陣對應元素的乘積和，ε為正則化系數，H(P)表示匹配概率矩陣P的熵。通過Sinkhorn 算法［15］求解式（5），最終該優化過程得到的最優聯合概率矩陣P*即為3D-2D 特征點之間的匹配概率矩陣。從P*中選取概率最高的N個元素，可以獲得N組3D-2D 點的匹配關系，利用該N組點即可進行后續的姿態求解。

2.3 基于隱式微分的可微姿態解算

利用2D-3D 特征點的匹配關系，在求解姿態時，首先使用基于隨機一致性抽樣（Random Sample Consensus，RANSAC）的P3P 算法濾除異常匹配點，然后使用EPnP［16］算法解算目標的姿態信息。但該求解過程是一個不可微的幾何優化過程，無法顯式解析計算每一步梯度，這會導致PnP 模型高精度位姿求解能力無法指導網絡訓練。為了將PnP 位姿求解過程納入整個網絡的學習過程，提高網絡對姿態的解算精度，本文采用隱式微分理論［17］完成位姿求解過程的梯度計算。對于整個位姿求解過程，將目標函數定義為重投影誤差函數，即：

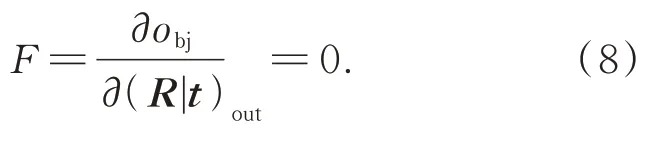
將重投影誤差函數obj對輸出(R|t)的一階偏導作為約束F，則位姿求解過程s對輸入i的雅可比矩陣可以寫為：

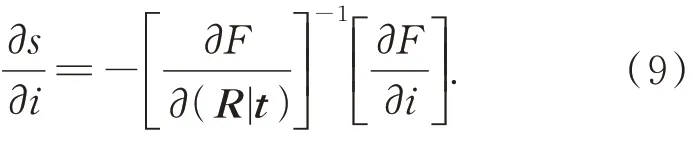
式（9）中，不涉及任何位姿求解的中間過程，直接得到了整個過程的雅克比矩陣。對于位姿求解的任何一個輸入量，其梯度都可以通過位姿求解層繼續反向傳播，梯度計算與求解過程中任意的不可微過程無關，從而將該求解過程和之前的特征提取、匹配過程集合在一個深度網絡中，實現優勢互補。

2.4 損失函數

位置和姿態在PnP 模型求解過程中是同時解出的兩個耦合量，因此在整個姿態求解過程中，網絡有兩個預測對象：特征點之間的匹配以及最終位姿。本文綜合考慮了兩個預測對象對網絡訓練的影響，采用雙損失函數對網絡訓練進行監督。即：

式中Lc，Lpose分別對應特征點匹配以及位姿求解任務的損失。衡量匹配結果的損失項Lc表示為：

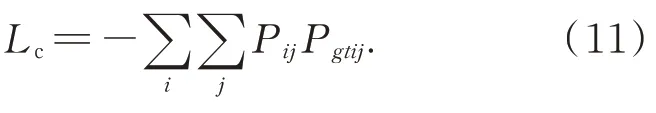
對于位姿損失項，本文對比了多種不同形式的損失函數，包括重投影誤差、加權重投影誤差和旋轉矩陣角度差等。其中，旋轉矩陣角度差作為損失函數的結果稍好于其他函數，因此本文采用的位姿損失函數為：

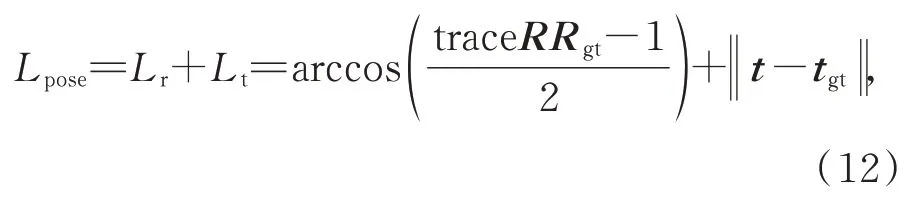
其中P，Pgt，R，Rgt，t，tgt分別表示概率矩陣、旋轉矩陣、平移矢量的解算值和真值。

由于使用了可微姿態求解模塊，該損失項可以直接用來指導網絡訓練，該損失項訓練模型直接驗證了可微姿態求解層的有效性。

3 數據集建立與網絡訓練

數據集對深度學習起到至關重要的作用，帶有位姿信息的大型公開數據集例如Kitti、YCBVideo 等基本利用人工標注的方法提供真實場景下的位姿標簽，數據量較小，且容易受傳感器標定精度等問題導致錯誤標注，不適用于激光跟蹤儀的高精度測量領域。因此，本文根據激光跟蹤儀大范圍高精度姿態測量的要求，基于激光跟蹤儀靶標上的特征點坐標，制作了一個具有豐富標注信息的數據集。

3.1 數據集制作

對于激光跟蹤儀的姿態測量問題，數據集中應該包括相對位姿(R|t)，相機內參K，2D-3D 特征點坐標及點之間的對應關系。由于實采數據并進行標注制作數據集的成本過高且無法保證標注信息的精度，數據集制作采用了更高效的方法，基于相機成像數學模型，利用靶標特征點的空間3D 坐標，通過改變外參獲得大量3D-2D 點對以及它們所對應的位姿以及2D 特征點坐標，此處2D 點坐標為消除內參影響的歸一化坐標（即假設內參固定）。這一設定可以使模型對任意輸入求解時內參固定為單位陣，只需對實際數據輸入的像素坐標進行簡單的預處理。

該方法降低了數據集制作的難度且保證了標注的精度，和實際拍攝圖像制作數據集的方法相比，雖然沒有考慮真實場景中可能存在的噪聲干擾，但由于模型本身具有一定的泛化能力，在實際場景硬件誤差得到較好控制的情況下，通過該數據集訓練的網絡可以獲得準確的姿態解算結果。數據集中樣本外參取值為激光跟蹤儀的工作范圍，即偏航角和俯仰角為±30°，橫滾角為±180°，距離為0～30 m 考慮到相機在跟蹤儀工作范圍內拍攝圖像時特征點不會相互遮擋以及后續姿態解算的穩定性等因素，激光跟蹤儀的測量靶標上采用非對稱非共面布局的14個紅外LED作為特征點，LED特征點的分布情況如圖4所示。

圖4 激光跟蹤儀靶標Fig.4 Laser tracker target

針對待測靶標，在測量范圍內隨機取值，生成了訓練集以及測試集。為了模擬真實情況，分別生成了與訓練集分布不同的理想測試集，以及在理想測試集中每一個2D 像素特征點上附加一個服從正態分布的隨機量的噪聲測試集，兩測試集中均包含5 324 組測試樣本且保證與訓練集分布不同。

3.2 網絡訓練

訓練過程基于Pytorch 框架，使用Adam 優化器，Adam 的兩個指數衰減超參數設置為0.9，0.999，學習率動態衰減，初始值為0.001 25，batch-size 設置為256。訓練過程在Linux 系統下，使用單塊RTX3090GPU，訓練完成后，在兩組測試樣本上驗證網絡性能，測試集中所有樣本均為在測量范圍內生成的隨機樣本且保證其分布與訓練集不同。

青椒葉片小，蒸騰量小，一般在坐果前不需澆大水，出現干旱時可澆小水。每次澆水要在晴天上午澆，提高棚內溫度，中午將潮氣放出，避免棚內濕度過大造成病害流行。底肥施足后，坐果前不用追肥，防止徒長，造成“三落”現象。

4 測試集結果分析

根據激光跟蹤儀的測量需要，本文使用RPY角的形式對姿態解算結果進行展示，并利用姿態角的測量值與真實角度值θgt的差作為對網絡解算值的評價指標，即：

選擇RANSAC 和SoftPosit 算法在測試集上與網絡進行對比。SoftPosit 算法是BPnP 問題的一種迭代求解方法，可以根據給定的初始值同時完成特征點的匹配以及姿態求解。考慮到實際應用中初始值獲取困難，本文選擇與真實值相差5°以及相差22.5°的兩種初值進行迭代求解。RACSAC 算法作為一種魯棒的位姿估計算法，在特征點存在誤匹配時可以有效地濾除異常點，測試中設置輸入RANSAC 算法進行求解的數據中50%的點存在錯誤的匹配關系。

為了反映測試集上的整體情況，定義姿態誤差小于e的樣本數占所有樣本的比例為r，并繪制了測試集的e-r曲線，如圖5 所示。其中，Sp5 和Sp22.5 分別表示不同初值的Softposit 算法，RANSAC 表示用RANSAC 算法直接求解。在數據集上進行消融實驗，圖5 中Losst表示完整網絡結構的測試集結果，Lossc代表不使用2.3 節介紹的可微PnP 求解模塊的測試集結果。需要說明的是，如果在特征提取網絡中，不使用上下文歸一化操作（CN），會使網絡難以訓練（loss 不收斂），該情況下的e-r曲線基本和x軸重合，因此在圖6 中沒有畫出該條曲線進行對比。但基于上下文信息對特征提取網絡進行改進后，網絡會提取到更有效的特征，大大提高特征點匹配的準確性以及最終解算出的姿態精度。

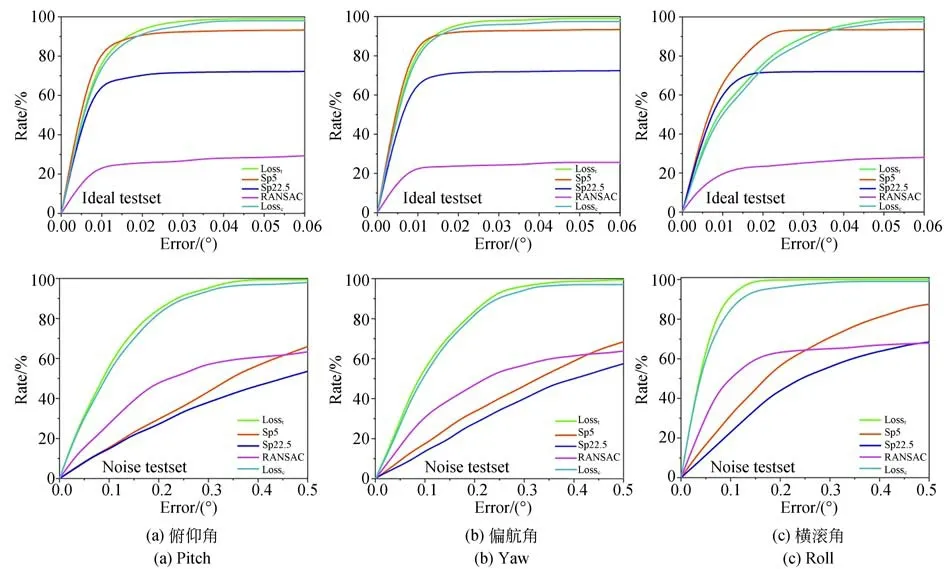
圖5 測試集的姿態測量結果Fig.5 Attitude measurement results of testset

4.1 理想測試集

理想測試集的結果如表1 所示。在提供較好的先驗信息的情況下，直接使用RANSAC 算法處理BPnP 問題耗時15 ms，但結果很差；Soft-Posit 算法平均耗時220 ms，運行收斂到全局最優時，姿態角誤差較小，但該算法的平均誤差以及均方根誤差均大于本方法，且該迭代算法對初始值很敏感；本文方法單次求解耗時約40 ms，解算精度最高，性能最優，能夠滿足激光跟蹤儀的要求。

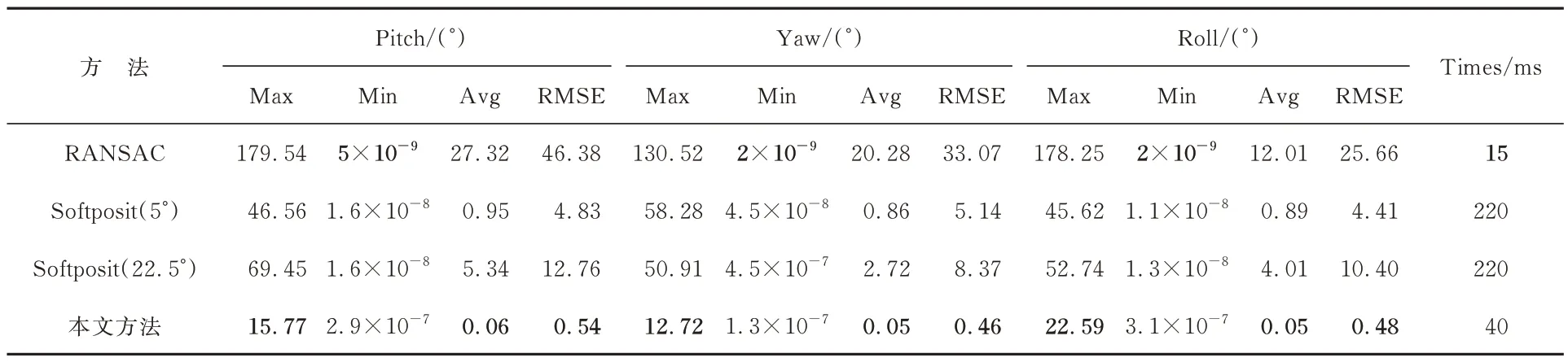
表1 三種算法的姿態測量結果Tab. 1 Attitude measurement results of three algorithms

圖6 利用網絡的位姿解算值對理想測試集中隨機兩個樣本的重投影誤差進行可視化，3D 特征點的投影點與2D 特征點基本重合，證明解算出的位姿參數精度較高。

圖6 隨機兩組樣本的重投影誤差可視化Fig.6 Visualization of reprojection errors for two random samples

4.2 噪聲測試集

在實際應用場景中，相機標定以及特征點坐標的獲取都會因外界條件干擾而產生誤差。為了模擬真實情況，在噪聲測試集上額外進行了一組對比，該測試集仿照真實情景，對每一個2D 特征點坐標附加一個符合正態分布的噪聲，結果如表1 所示。由表1 可知，姿態解算精度受特征點坐標提取的影響較大；俯仰角和偏航角比橫滾角更容易受誤差的影響；俯仰角和偏航角的求解精度相當且小于橫滾角精度。結合4.1 節的分析可知，當存在噪聲時，本方法的精度和速度仍然優于對比算法。

5 實 驗

本文搭建的姿態測量實驗平臺如圖7 所示。首先，將相機架設在自主開發的三自由度激光跟蹤儀上，對跟蹤儀配套的測量靶標進行姿態測量。由于激光跟蹤儀實際應用的場景通常比較復雜，為了使相機具有較好的圖像穩定性以及強抗干擾能力，以高分辨率和高采樣速率為前提，選用DELSA 公司生產的高速工業相機，其分辨率為2 432×2 048，像元尺寸為3.45 μm。

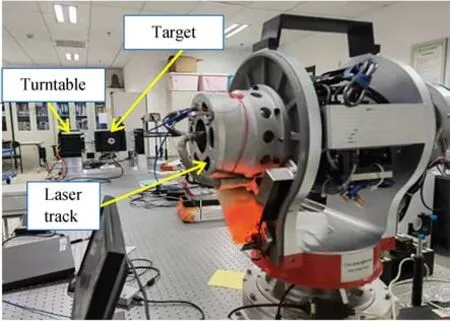
圖7 姿態測量系統實驗平臺Fig.7 Experimental platform of attitude measurement system

將靶標安裝在高精度轉臺上，該二軸轉臺的俯仰角定位誤差小于2.8″，橫滾角定位誤差小于7.9″，跟蹤儀和轉臺之間的距離為3 m。跟蹤儀保證靶標保持在相機視場的中心，高速相機可以在轉臺轉動時采集到清晰的圖像用于姿態解算。通過電腦控制轉臺轉動帶動靶標運動，使用轉臺的轉動值為標準值，與測量值進行對比，確定測量精度。測量過程中，首先對相機采集圖像進行腐蝕、膨脹、濾波、二值化和質心提取等預處理得到2D 特征點坐標，如圖8 所示。

圖8 圖像預處理過程Fig.8 Image preprocessing process

由于高速相機圖像的采集速度大于姿態解算速度，因此制約系統測量速度的主要因素是姿態的解算時間（約40 ms）。在該用時下，系統基本能夠對靶標的不同轉動速度進行實時響應，滿足跟蹤儀的動態測量要求。

對圖像預處理得到的2D 特征點坐標使用相機內參矩陣進行處理后，配合靶標上3D 特征點坐標即可求解姿態。在姿態測量實驗中，由于轉臺只能繞兩軸旋轉（俯仰角、橫滾角），無法進行偏航角的測量實驗。為了保證高精度二軸轉臺轉動時姿態解算值不受偏航角分量的干擾，測量之前使兩坐標系之間的3 個姿態角盡可能為0°。具體來說，手動完成特征點匹配并利用EPnP 算法確定兩坐標系之間較準確的位姿初始值，然后將該初始值放入SoftPosit 算法中運行至收斂，從而確定兩坐標系之間的3 個姿態角。根據解算結果對轉臺以及跟蹤儀進行精密調節，從而將初始的3 個姿態角控制在10-4°左右，基本消除了偏航角分量的影響。

轉臺實際轉動的角度與網絡解算出的角度如表2 和表3 所示。由于轉臺只能繞兩軸旋轉，因此表中數據是俯仰角以及橫滾角的實驗結果，缺少偏航角的相關數據。由表可知，在3 m處，±30°內本方法最終解算出的俯仰角誤差優于0.31°，橫滾角誤差優于0.03°。

表2 俯仰角實驗結果Tab. 2 Experimental results of pitch （°）

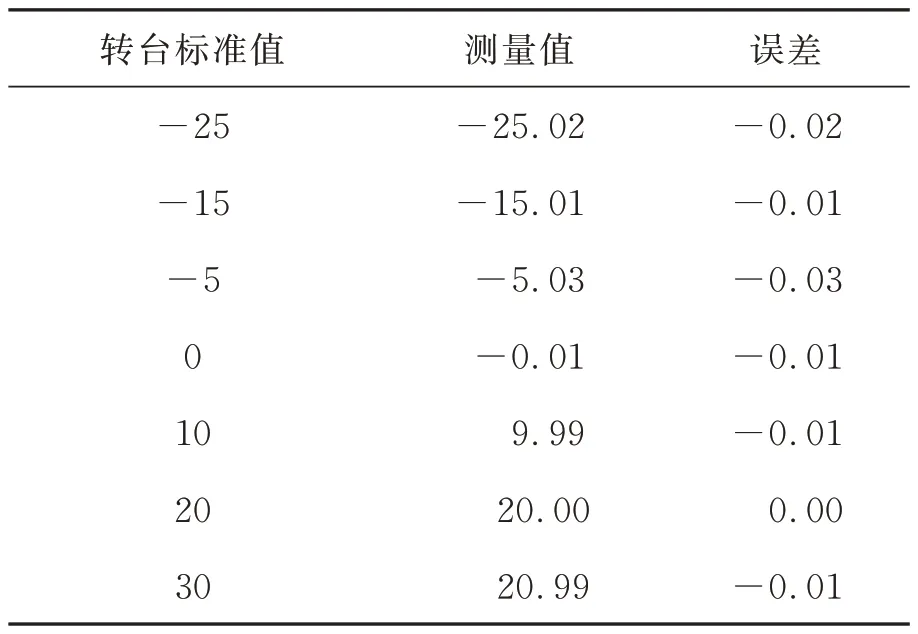
表3 橫滾角的實驗結果Tab. 3 Experimental results of roll （°）

目前，面向激光跟蹤設備的高精度姿態測量方法包括基于位置敏感器的姿態測量方法［18］、基于傳統單目視覺的測量方法［19］以及利用兩者冗余信息進行融合優化的方法［20］等。這些方法和本文提出方法的實驗條件以及實驗結果對比如表4 所示。

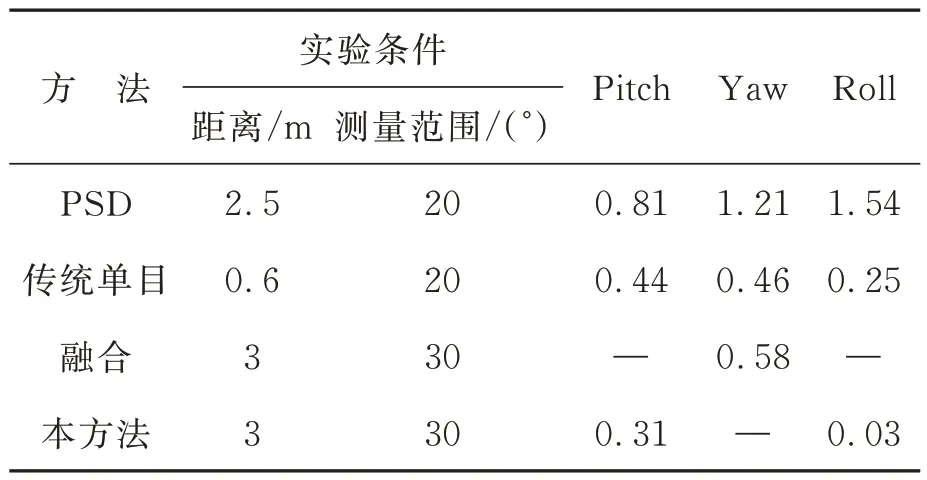
表4 不同方法測量姿態的實驗結果對比Tab. 4 Comparison of experimental results of attitude with different methods

由于實驗條件的不同，表4 中有部分姿態實驗數據在文獻中沒有給出，但根據本文的仿真結果，本方法對于俯仰角和偏航角具有近似的解算精度，且該精度低于橫滾角的解算精度，因此本文方法的姿態角解算精度優于其他方案。

6 結論

為了使自主研發的三自由度激光跟蹤儀具備六自由度的測量能力，本文研究并設計了一個姿態自動測量網絡。該網絡結合了深度學習特征匹配能力與幾何PnP 位姿求解算法的優勢，實現了姿態的快速高精度解算。基于二維高精度轉臺的姿態測量實驗表明，該方法的橫滾角解算誤差小于0.03°，俯仰角誤差小于0.31°，解算時間約為40 ms，具有較好的測量精度以及實時性，相比于目前已有的姿態測量方法，速度和精度均有所提升，且可以實現姿態的自動測量，對實現激光跟蹤儀的姿態快速測量具有重要參考價值。通過在3 m 處進行測量實驗驗證了本方法的性能，但考慮到不同距離下特征點坐標的精度會影響最終的姿態解算精度，未來的工作將從靶標特征點的布局、紅外LED 選型以及相機標定、圖像預處理算法等方面進行改進，進一步提高本方法的姿態測量精度。